DOI: 10.11817/j.issn.1672-7207.2015.05.013

无线传感器网络中分布式延迟受限低能耗数据收集算法

陈零，奎晓燕，张士庚，王建新

(中南大学 信息科学与工程学院，湖南 长沙，410083)

摘要：集中式数据收集算法难以实际应用于外部环境恶劣、实时性要求高的无线传感器网络场景中。为解决此问题，采用分布式思想来构造算法，从而提出一种易于实现且有效的算法DBEGA(distributed delay-bounded energy-efficient data gathering algorithm)。DBEGA算法的基本步骤是：先生成1棵最少跳数的数据收集树来满足特定应用中延迟受限的要求；在此基础上，借用时间复用的方法，将一特定长度的时间段分割成n个等长的独立时间片，然后将这些时间片唯一地分配给每个节点，每个节点就能互不干扰地对已生成的数据收集树进行调整，使得各个节点的负载尽量均衡，从而达到延长网络生命周期的目的。研究结果表明：与随机路由和分布式算法LMST相比，DBEGA所构造的数据收集树能够在满足延迟受限要求的同时将网络生命周期提高20%以上。

关键词：无线传感器网络；数据收集；数据收集生成树

中图分类号：TP301            文献标志码：A         文章编号：1672-7207(2015)05-1655-08

Distributed delay-bounded energy-efficient algorithm for data gathering in wireless sensor networks

CHEN Ling, KUI Xiaoyan, ZHANG Shigeng, WANG Jianxin

(School of Information Science and Engineering, Central South University, Changsha 410083, China)

Abstract: The centralized data gathering algorithms are difficult to be used in the high dynamic wireless sensor networks. For solving the problem, a distributed delay-bounded energy-efficient data gathering algorithm (DBEGA) was proposed, and a delay-bounded data gathering tree was constructed. DBEGA algorithm involves two steps. In the first step, the minimum hop count tree was constructed in a distributed manner for meeting the requirements of being delay-bounded. In the second step, DBEGA divided a specific length of time into n equal-length independent time slices and these time slices were uniquely assigned to each node. So an undisturbed environment was created for every node to adjust the load of nodes in the generated tree to balance energy consumption of different nodes, which effectively extended the lifetime of the network. In the adjustment, both the number of children of a node and their residual energy were considered. The results show that DBEGA achieves better tradeoff between delay and network lifetime than LMST algorithm, and it can prolong the lifetime by 20%.

Key words: wireless sensor networks; data gathering; spanning tree

近几年来，对无线传感器网络的研究一直是热点。其最基本的应用是通过部署好的无线传感器节点对某块区域进行特定目的监测，并将感知的特定信息通过无线方式传送到远程基站(Sink)进行后续处理。一般来说，部署在监测区域的无线传感器节点由于各种原因，其能量无法补充，当自身能源耗尽时就意味着节点死亡：因此，如何在监测过程中尽量降低节点能耗，从而延长网络的整体生命周期，是无线传感器网络协议设计的主要目标之一。相关研究表明，传感器节点的能量主要消耗在各种通信上，而对感知数据的传输是通信开销的主要来源，所以，设计能量高效的数据收集算法，对于延长无线传感器网的生命周期具有重要意义^[1]。另一方面，在一些需要快速反应的监测应用场景如森林火灾监视、矿坑瓦斯预警、战场信息监控中，不仅要尽可能地延长无线传感器网络的生命周期，而且需要尽快地将感知信息传递到基站进行分析和处理^[2]。这就要求数据收集算法不仅要考虑网络生存周期延长，而且需要使得网络延迟尽可能短。如何构建满足网络延迟限制的数据收集树也是目前无线传感器网络领域的一个重要研究问题。在多跳无线传感器网中，网络延迟与感知节点到达基站节点所经过的跳数有直接关系，跳数越少，延迟越短。而根据图的相关理论，跳数可以转化为数据收集生成树的高度，所以，生成1棵最低高度的数据收集生成树可以让多跳传感器网的延迟大大缩短。算法DB-MDST^[3]和MILD^[4]等都是针对延迟受限提出的基于树的集中式数据收集算法。其中，MILD是DB-MDST的改进算法，它利用一种均衡最少跳数收集树中节点度的方法，在保证网络延迟较短的情况下，能有效延长网络的生命周期。然而，在某些延迟受限的特定应用如战场信息监控、火山监测预警中，由于客观环境的极端不确定性，传感器节点很容易被损毁，为有效监测某一区域，需布撒大量节点进行冗余覆盖^[5-8]。从成本上考虑，传感器节点的运算和存储能力将十分受限，基站节点也不能部署在监测区域之内(因基站成本较高，不能经常损毁)，这样就会要求各个节点轮流担任临时基站的角色，而集中式算法对节点的运算和存储要求较高，已不适用于这种情形。为此，本文作者提出一种新的分布式数据收集算法DBEGA(distributed delay-bounded energy-efficient data gathering algorithm)，其通信开销小，对节点运算能力要求低，特别适用于上述应用场景。

1  相关工作

目前，基于树的数据收集算法在保证网络连通性和可靠性方面具有天然的优势，而且具有保证QoS、便于实现高效的能量管理等优点，是目前研究的热点。 在早期的典型树收集算法中，重点关注的是网络整体的生命周期，对于网络延迟基本忽略。下面简要介绍几种方法。

PEDAP-PA^[9]从1棵只包含Sink节点的树出发，以树外节点和树上节点间的通信代价作为权值，不断挑选权值最小的节点加入树，直至网络中所有节点加入树为止。MNL是对PEDAP-PA的改进^[10]，设计了更合理的权值来挑选节点加入树。然而，PEDAP-PA和MNL在构造生成树的过程中，树外节点是作为叶子节点被考虑并加入树，在树没有最终建立前无法确定1个节点最终在树上拥有多少孩子，因此，它们的生成树往往存在节点负载不均衡、树的高度无法控制等情况。IAA从1棵任意树出发，迭代地选择1条能使“瓶颈节点”包含在1个圈中的任意边加入树，然后，删除该“瓶颈节点”在圈中关联的任意1条边以使“瓶颈节点”的度减少１并打破圈^[11]。IAA能做到生成树上节点负载均衡，树的生命周期达到近似最优。但是，树的高度也无法控制。

比较典型的以网络延迟受限为前提要求的算法有DB-MDST和MILD。MILD是对DB-MDST的改进，它通过限定树的高度来满足延迟要求，然后通过使树上“瓶颈节点”的度最小化来延长树的生命周期。

上面所述算法均为集中式算法，其对节点运算能力要求高，通信开销大，不适用于客观环境极为恶劣的应用场景。而分布式算法的运算复杂度低，其通信开销远比集中式算法低，适用于网络动态性很高的应用场景。随机路由^[12]和最近提出的LMST^[13]是2种典型的分布式数据收集算法。

随机路由的基本思想如下。首先由Sink节点广播建树消息。邻居节点接收到此消息后，将消息内容重设，然后继续广播修改过的建树消息。依此类推，只要网络是连通的，则在建树消息传播一段时间后，1棵数据收集树便建立起来。通过建树消息中的控制参数，随机路由可以构建最少跳数的数据收集树。然而，其没有对各个节点进行均衡控制，很容易产生能耗瓶颈节点，会明显缩短网络的整体生命周期。

LMST(local minimum spanning tree)算法是1个基于随机路由的分布式改进算法。它利用节点间距离和通信能耗之间的关系对数据收集树进行调整，以达到减少能量开销进而延长网络生命周期的目的。此算法在建立局部最小生成树时，节点间至少需要进行2次消息交换，其后还要进行多次控制交互，所以，其通信开销比较大。并且由于需要获取各节点间链路能耗，必须知道各节点的坐标信息，这必然也会增大通信开销。虽然LMST算法可以使得收集树节点的度接近最小，从而在节点能对感知数据完全聚合的情形下，达到传感器网络的生命周期理论上界。这里的度是指节点在树中的孩子数。但LMST算法网络延迟性能很差，完全无法保证感知数据传输的实时性要求。

针对上述问题，本文作者提出1种DBEGA算法。其基本过程是：先随机选择1个节点作为临时基站，再以此节点为根节点随机生成1颗最少跳数的初始数据收集树，然后，利用分布式方法对每个节点的度进行优化调整，在网络延迟和生命周期间取得一个较好的平衡。算法在运行过程中的计算和通信开销都较小，适用于网络拓扑因客观环境的影响而经常变化的应用场景。

2  网络模型和问题描述

2.1  网络模型

在1个面积为M×M的正方形区域A内随机布撒n个传感器节点，这样形成的传感器网络可以用1个连通的无向图G(V, E)来表示。其中：V为节点集合，V={v₁, v₂, …, v_n}； |V|=n；v₁, v₂, …, v_n为传感器节点；E为G中边的集合。假如节点v_i和v_j都在对方的通信半径之内，则边(v_i, v_j)∈E，|E|=m为边的数量。假设网络具备如下性质：

1) 整体网络是连通的，节点在部署后不再移动。

2) 节点无法进行能源补充，且初始能量可以互不相同。

3) 节点之间利用已有的同步算法进行了毫秒级精度的时间同步^[14]。

不失一般性，假设节点在发射和接收数据时的功率固定，用E_t表示发射1 bit数据需要的能量，E_r表示接收1 bit数据需要的能量。同时假定网络拥有较好的拥塞控制策略，可避免数据在传输过程中发生拥塞和重传。

2.2  相关定义

本文所研究的无线传感器网络中，节点会对感知数据进行完全聚合(fully aggregate)^[15-16]，即在1轮数据收集过程中，每个非叶节点会接收多个来自孩子节点的长度为k bit的数据包，然后与自己产生的k bit数据进行聚合，最终生成1个长度也为k bit的聚合数据包发送给父亲节点。参考文献[4]，给出以下定义。

定义1  轮。是指所有传感器节点收集1次数据，并将数据传送到Sink节点所要耗费的时间，不管此时间要持续多久。

定义2  节点生命周期。是指节点v_i在1棵收集树中存活的轮数。用E(v_i)表示节点剩余能量，用e表示1个给定的阀值。当节点能量小于e时，将无法完成1轮的数据收集任务，因此，可以用E(v_i)＞e来判断节点是否存活(若E(v_i)＞e，则节点存活，反之，则节点死亡)。节点生命周期可用下式计算：

  (1)

其中：k 为节点每轮感知数据的平均长度(单位为bit)；D(v_i)表示节点v_i在树T中的度数。

定义3  树的生命周期。是指在数据收集过程中，第1个死亡的节点所经历的轮数，就是树T的生命周期。可用下式表示：

         (2)

树的生命周期可等同为网络的生命周期。

定义4  最优树。就是所有数据收集生成树中生命周期最长的那棵树，可表示为

      (3)

式中：T*为指网络G中任意1棵生成树；T_S(G)为G中生成树的集合。

定义5  瓶颈节点。是指收集树T中最早耗尽能量的节点，其生命周期就相当于树的生命周期。

2.3  问题描述

多跳无线传感器网络的延迟主要受树的深度和树中节点的孩子数量等因素的影响，其中树深对延迟的影响最大^[4]，因此，在基于树的数据收集算法中，生成1棵深度最小的数据收集树，会使网络整体延迟近似于最短。网络中节点数n等于树中各层节点孩子的总和，即

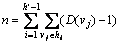           (4)

其中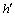：为树深；h_i为树上第i层所有节点的集合；D(v _j)为节点j的度数。根据式(4)，若树中每个节点的度数最小，则树的深度最大；若树中每个节点的度数最大，则树的深度最小。然而，为使得网络延迟最小，需最小化树深度，这样可能会使树中某些节点的度增加。根据式(1)和(2)，得

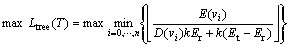(5)

由于E_r和E_t是固定的，只有D(v_i)可以调节，因此，可以将其作为主要的优化目标。为了简化表达，对式(5)进行等价变换：

        (6)

其中：c=E_t/E_r-1。根据式(6)，在完全聚合的情况下，节点在生成树中的度数直接与整个网络的生命周期相关，即节点的平均度数越小，网络生命周期越大。然而，根据式(3)，当数据收集树的节点平均度数最小时，网络生命周期最大，同时树的深度也最大。所以，网络延迟的缩短和生命周期的延长是互相矛盾的，不可能同时实现。

本文针对上述问题，提出1种分布式的算法DBEGA，在保证延迟受限的前提下，尽可能地平衡各节点的度数，使得网络生命周期尽可能地延长。此外，DBEGA具有运算和通信开销低的特点，在客观环境极端恶劣的应用场景中，相比于集中式算法，具有更好的综合性能。

3  DBEGA的设计和分析

分布式算法只能利用局部信息来达到优化目标，同时要尽量减少通信开销。所以，需要找到合适的网络参数和控制方法来进行有效平衡。

3.1  DBEGA算法的描述

文献[4]指出，在聚合收集情形下，节点在收集树中的度数与节点能耗成正比关系，即收集树中的节点平均度数越小，树的生命周期越长。可以用节点孩子数代替度数，作为算法运行的控制参数。在这种情况下，本文算法所要解决的问题实际上是在1棵已生成的最少跳数数据收集树中，通过一定的优化调整使每个节点的度尽量地小，从而达到延长网络生命周期的目的。

这里采用1种时间片轮转的方法来减少算法运行过程中节点间的通信开销。其基本思想是：为每个节点分配唯一的时间片，使得各节点在运行算法时不会互相干扰，如此能大大减少控制消息的发送和接收，从而达到降低通信开销的目的。为了保证每个节点分配到的时间片是唯一的，可以在节点布撒之前，为每个节点设定1个唯一的整数(若为100个节点，则整数范围为0~99，以此类推)，通过这个整数来保证每个节点分配到的时间片的唯一性。

目前无线传感器节点的理论传输速度普遍可达250 kbit/s^[17-21]。对于中等规模的无线传感器网络，节点地址可用16 bit的短地址表示，加上一些必要的标志位和网络参数信息，协议控制帧的长度可控制在32~64 bit之间，如此可保证节点间控制帧的交互可在1 ms内完成。所以，在本文算法中，将时间片长度设定为1 ms。

用1个例子直观地说明DBEGA算法的效果。图1所示为数据收集算法生成树的例子示意图，其中：图1(a)所示为1棵随机路由生成树，三角形灰色点为Sink节点，灰色圆点为瓶颈(负载)节点，因为其度数最大(度数为7)； 图1(b)所示为经由算法DBEGA优化后的生成树。从图1可以看出：灰色圆点的度数已降低为4，则根据定义2和定义3，图1(b)所示的生命周期为图1(a)所示生命周期的2倍。由此可知：优化的关键是要将瓶颈节点的孩子节点合理调整到非瓶颈节点上。

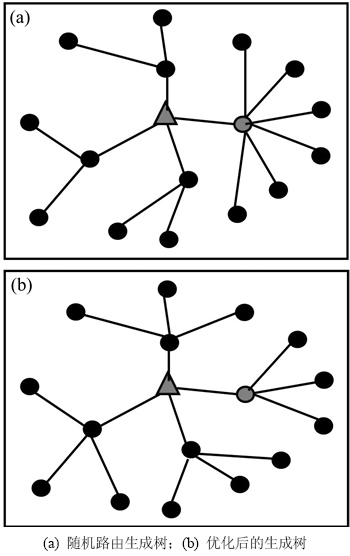
图1  数据收集算法生成树示意图

Fig. 1  Spanning tree of data gathering algorithm

DBEGA算法的基本步骤如下。

1) 随机选取1个节点作为临时基站，同时，每个节点收集其邻居节点信息，然后利用随机路由，以临时基站作为根节点，构造最少跳数的初始数据收集树。各节点要获取其所有邻居节点的编号、每个邻居节点的孩子数以及自身在树中的层数。

2) 除初始树的第1层节点外，为剩下的每个节点分配互不干扰的时间片。

3) 在每个时间片内，节点运行优化调整算法。具体过程为：在上层邻居节点中，选取孩子数(可以将邻居节点数也同时考虑)最小(这个值要比当前父节点的孩子数至少小2)的那个节点作为新的父亲节点。若选取了新的父亲节点，则向新旧父亲节点发送确认信息；若新旧父亲节点收到了确认信息，则要广播1个更改信息，通知其邻居节点修改与其相关的孩子数量。

4) 当每个节点的调整时间片运行完毕时，1颗优化后的数据收集树构造完成，开始进行数据收集工作。

5) 当有节点死亡或经过几轮数据收集后，重启算法过程。

3.2  DBEGA算法分析

对于DBEGA的时间开销，把它分为3个阶段进行分析：一是邻居信息收集阶段，设节点数为n，此阶段所花时间一般会预设为1个常数T_N，大小与n呈线性正比关系(复杂度为O(n))，单位为秒级；二是随机路由阶段，所花时间T_S与n呈线性正比关系(复杂度为O(n))，单位也为秒级；三是树调整阶段，时间片长度为1 ms。由算法过程可知，此阶段所用时间为n(h-1)(h为数据收集树的高度)，将其除以1 000，单位也化为ms级。综上所述，算法的整体时间消耗为O(nh)。

DBEGA的通信开销相当小，根据其算法过程，每个节点只需要收集1跳内的邻居节点信息，然后只需有限的几次控制交互就能达到算法运行的目的。完成这些动作所需能耗与节点在一轮数据收集中所用能耗相比，可以忽略不计。

为了进行比较，这里分析集中式算法MILD的通信开销。MILD的算法过程分为2个阶段：首先为信息收集阶段。在此阶段中，各节点是沿初始收集树将所需信息传送到Sink节点。假设d _i表示节点i的子孙节点数，地址和相关信息数据包长度为64 bit，则节点通信开销为64E_rd_i+64E_t(d_i+1)。第2个阶段是Sink节点进行运算后，要将优化树传播到各节点。假设优化树用数组形式存储，数组单元长度为16 bit，n代表节点数量，则在此过程中，各节点的通信开销为16(n-1)(E_r+E_t)。可见：在MILD的整个算法运行过程中，节点的通信能耗与网络节点数量成正比关系，其远大于DBEGA算法中的节点通信能耗。此外，可推知MILD算法中，Sink节点的通信能耗为64E_rn+16(n-1)E_t。可见：Sink节点的通信开销也与网络节点数呈正比关系，在客观环境极为恶劣的应用场景中，由各节点轮流担任临时Sink。若使用MILD算法，则过高的通信开销会使担任临时Sink的节点过早耗尽能量而死亡，而使用本文提出的DBEGA算法能很好地解决这个问题。

3.3  DBEGA与LMST的对比分析

在感知数据完全聚合的情况下，LMST算法的网络生命周期性能已接近理论最优上界，但这是以增大网络延迟性能为代价的。

图2所示为算法DBEGA和LMST的生成树示例。图2(b)所示为LMST算法的数据收集生成树，与图2(a)所示的DBEGA数据收集生成树相比，其节点最大度数为2，后者的节点最大度数为4。由定义2和3可知：在图2中，LMST算法的网络生命周期为DBEGA网络生命周期的3倍；然而，LMST算法生成树的深度也为DBEGA的3倍。由前面分析，无线传感器网络延迟与数据收集树的深度呈正比关系，所以，LMST的网络延迟大大高于DBEGA的网络延迟。

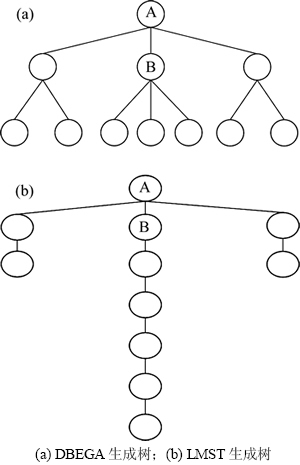
图2  DBEGA算法和LMST算法的生成树对比

Fig. 2  Spanning tree comparison of DBEGA and LMST

LMST算法是专为相关数据收集而设计的，它的侧重点是尽量减少每个节点的度数，并不对数据收集生成树的深度进行任何限制。虽然它的网络生命周期性能很理想，但会导致网络延迟较高，不适用于对实时性有要求的应用场景。

4  模拟实验

基于NS2(版本号2.33)进行仿真以评价所提出算法的性能。为了验证算法的扩展性和有效性，以节点密度和Sink节点的位置为可变参数对实验场景进行设置，具体如下所示：区域面积为100 m×100 m；节点数量为100，200，300和400个；节点最大通信距离为20 m。节点的数据产生率为 1 000 bit/轮。为了使所有算法能进行公平对比，节点均采用固定发射功率，发送能耗E_t大约是接收能耗E_r的 2倍，即 E_t=2E_r，E_r=50 nJ/bit^[4]。因为路由构造和网络调整时的控制通信开销可以独立分析，所以，进行模拟实验时，只关注数据收集时的通信能耗和树的生命周期。此外，节点对感知数据进行完全聚合。实验结果是算法执行20次后的平均值。

4.1  选取中心节点作为临时Sink的各算法对比

图3所示为临时基站处于区域中央时各算法在不同节点数情况下的网络生命周期对比曲线。在模拟实验中，DBEGA算法的生命周期无论在何种节点密度下都比随机路由的长，平均生命周期提高27%。MILD是梁俊斌等^[4]提出的较优秀的延迟受限集中式算法，它的生命周期要高于DBEGA，大约为DBEGA的1.6倍。但MILD算法的时间复杂度要远比DBEGA的复杂度高^[4]，在节点运算能力受限以及网络拓扑经常变化的情况下，MILD算法难以得到实际应用，此时，DBEGA可以作为MILD的理想替代算法。

图3  临时基站在区域中心时各算法生命周期对比

Fig. 3  Comparison of different algorithms networks lifetime when Sink node is in central region

从图3可见：LMST算法的生命周期提高，优于MILD算法，而且当节点密度变化时，其性能损失也很小，基本上已达理论最优上界。但LMST是通过增大网络延迟来获得生命周期性能的最优化，图4所示曲线很好地说明了这一点。数据收集树的深度越大，网络延迟也就越大。从图4可看出：LMST算法生成树的深度要明显比其他3种算法的深度高，而且随着节点密度的增加，这种差距也显著增大；当区域内节点数量为400时，LMST的数据收集树深度为其他3种算法的6倍，所以，它完全不适用于延迟受限的应用场景。

图4所示为不同算法生成树的深度对比曲线。从图4可见：DBEGA算法的数据收集树深度相对最低，因为它是以最少跳数为控制参数来构造数据收集树，这能最优化树深。所以，综合来说，在延迟受限的应用场景中，DBEGA是一种适用性和实用性都很强的算法。

图4  临时基站在区域中心时各算法数据收集树高度对比

Fig. 4  Comparison of different algorithms spanning tree height when Sink node is in central region

4.2  选取边缘节点作为临时Sink的各算法对比

为验证算法的有效性和扩展性，从区域边缘选取临时Sink节点进行模拟实验。

图5所示为临时基站处于区域边缘时各算法在不同节点数情况下的网络生命周期对比曲线。当临时Sink处于区域边缘时，与随机路由相比，DBEGA的生命周期增加得更加明显，其平均增长比达33%。这是因为在区域的边缘，节点自身的邻居节点数较少，对于没有任何负载均衡机制的随机路由更容易产生度数很大的瓶颈节点，从而使其生命周期进一步降低。在此情况下，MILD算法的生命周期也受到影响，使得DBEGA的周期接近于MILD算法的65%。

图6所示为不同算法生成树的深度对比曲线，LMST算法的生命周期性仍是最长的。但从图6可看出：其数据收集树的深度依然很大，且随着节点密度的增加而呈线性增加，平均高出其他3种算法的4倍以上。

综上所述，DBEGA算法在网络延迟和生命周期间取得了有效平衡，且时间复杂度低，通信开销小，与其他算法相比，特别适用于延迟受限、Sink节点能力受限且网络拓扑动态变化大的应用场景。

图5  临时基站在区域边缘时各算法生命周期对比

Fig. 5  Comparison of different algorithms networks lifetime when sink node is in edge region

图6  临时基站在区域边缘时各算法数据收集树高度对比

Fig .6  Comparison of different algorithms spanning tree heights when sink node is in edge region

5  结论

1) 所提出的分布式数据收集算法(DBEGA)能很好地应用于战场监控、恶劣环境监测等网络动态性高的场景中。DBEGA通过为每个节点分配单独时间片，大大减少了节点间通信开销，同时也大大降低了算法复杂度，易于在计算性能有限的无线传感器节点上进行部署。

2) DBEGA算法是基于最少跳数生成树对网络生命周期进行优化，能有效抑制网络延迟，满足某些实时性要求高的应用场景。

3) DBEGA在保证网络延迟受限的前提下，与随机路由相比，网络生命周期提高20%以上。

参考文献：

[1] Rezaei Z, Mobininejad S. Energy saving in wireless sensor networks[J]. International Journal of Computer Science & Engineering Survey, 2012, 3(1): 23-37.

[2] Jr Simplfcio M A, Barreto P S L M, Margi C B, et al. A survey on key management mechanisms for distributed wireless sensor networks[J]. ComputerNetworks, 2010, 54(15): 2591-2612.

[3] Kwon S, Kim J, Kim C. An efficient tree structure for delay sensitive data gathering in wireless sensor networks[C]// O’Conner L. Proceedings of the IEEE 22nd International Conference on Advanced Information Networking and Applications. Washington D C, USA: IEEE Computer Society, 2008: 738-743.

[4] 梁俊斌, 王建新, 陈建二. 在传感器网络中构造延迟限定的最大化生命周期树[J]. 电子学报, 2010, 38(2): 345-351.

LIANG Junbin, WANG Jianxin, CHEN Jianer. On the construction of a delay-constrained maximum lifetime tree in wireless sensor networks[J]. Acta Electronic Sinica, 2010, 38(2): 345-351.

[5] Goyal D, Tripathy M R. Routing protocols in wireless sensor networks: A survey[C]// Guerrero J E. 2012 Second International Conference on Rohtak. Haryana, India: IEEE Computer Society, 2012: 474-480.

[6] Shih E, Cho S H, Ickes N, et al. Physical layer driven protocol and algorithm design for energy-efficient wireless sensor networks[C]// Rose C. Proceedings of the 7th Annual International Conference on Mobile Computing and Networking. New York, USA: ACM, 2001: 272-287.

[7] Akyildiz I F, Su W Y, Sankarasubramaniam Y, et al. Wireless sensor networks: A survey[J]. Computer Networks, 2002, 38(4): 393-422.

[8] Oliveira L M, Rodrigues J J. Wireless sensor networks: A survey on environmental monitoring[J]. Journal of Communications, 2011, 6(2): 143-151.

[9] Tan H O, Korpeoglu I. Power efficient data gathering and aggregation in wireless sensor networks[J]. SIGMOD Record, 2003, 2(4): 66-71.

[10] LIANG Weifa, LIU Ruzhen. Online data gathering for maximizing network lifetime in sensor networks[J]. IEEE Transactions on Mobile Computing, 2007, 6(1): 2-11.

[11] Wu Y, Fahmy S, Shroff N B. On the construction of a maximum-lifetime data gathering tree in sensor networks: NP-completeness and approximation algorithm[C]// Meril D. The 27th Conference on Computer Communications. Phoenix, AZ, USA: IEEE, 2008: 1013-1021.

[12] Han K H, Ko Y B, KimJ H. A novel gradient approach for efficient data dissemination in wireless sensor networks[C]// Matsunaga S. Vehicular Technology Conference 2004. Los Angeles, USA, 2005: 2979-2983.

[13] Tan H O, Korpeoglu I, Stojmenovic I. Computing localized power-efficient data aggregation trees for sensor networks[J]. IEEE Transactions on Parallel and Distributed Systems, 2011, 22(3): 489-500.

[14] Sami M L, James M C. Time synchronization in wireless sensor networks: A survey[C]// Conrad J. IEEE SoutheastCon 2010. Concord: NC, USA: IEEE, 2010: 242-245.

[15] Ozdemir S, Xiao Y. Secure data aggregation in wireless sensor networks: A comprehensive overview[J]. ComputerNetworks, 2009, 53(12): 2022-2037.

[16] JI Shouling, HE Jing, PAN Yi. Continuous data aggregation and capacity in probabilistic wireless sensor networks[J]. Journal of Parallel and Distributed Computing, 2013, 73(6): 729-745.

[17] Francesco M D, Anastasi G, Conti M. Reliability and energy-efficiency in IEEE 802.15.4/ZigBee sensor networks: An adaptive and cross-layer approach[J]. IEEE Journal on Selected Areas in Communications, 2011, 29(8): 1508-1524.

[18] Martalo M, Buratti C, Ferrari G, et al. Clustered IEEE 802.15.4 sensor networks with data aggregation: Energy consumption and probability of error[J]. Wireless Communications Letters, IEEE, 2013, 2(1): 70-73.

[19] Hagkighi M S, YANG Xiang, Varadharajan V, et al. A stochastic time-domain model for burst data aggregation in EEE 802.15.4 wireless sensor networks[J]. IEEE Transactions on Computers, 2015, 64(3): 627-639.

[20] Wang L H, Chen T Y, Lin K H. Implementation of a wireless eca acquisition soc for IEEE 802.15.4 (ZigBee) application[J]. IEEE Journal of Biomedical and Health Informatics, 2015, 19(1): 247-255.

[21] Amaro J P, R, Ferreira F J T E, et al. Device and operation mechanism for non-beacon IEEE 802.15.4/ZigBee nodes running on harvested energy[J]. Ad Hoc Networks, 2015, 26(1): 50-68.

(编辑  陈灿华)

收稿日期：2014-06-12；修回日期：2014-08-21

基金项目(Foundation item)：国家自然科学基金重点资助项目(61232001)；国家自然科学基金面上资助项目(61472449)；国家留学基金资助项目(2015[3012])；湖南省自然科学基金资助项目(2015JJ4077) (Project(61232001) supported by the Key National Natural Science Foundation of China; Project(61472449) supported by the General Program of the National Natural Science Foundation of China; Project(2015[3012]) supported by China Scholarship Council; Project(2015JJ4077) supported by the Natural Science Foundation of Hunan Province, China)

通信作者：奎晓燕，博士，副教授，硕士研究生导师，从事无线传感器网络数据收集协议的研究；E-mail: xykui@csu.edu.cn