DOI: 10.11817/j.ysxb.1004.0609.2021-40035

孪晶距对纳米钨力学性能影响的分子动力学模拟

薛克敏，张勇强，王路生，严思梁，李  萍

(合肥工业大学 材料科学与工程学院，合肥 230009)

摘  要：为了研究孪晶间距的大小对纳米钨力学性能及变形机理的影响，利用分子动力学对不同孪晶间距的孪晶钨进行了单轴拉伸模拟。使用近邻列表技术(CNA)和位错分析方法(DXA)对拉伸过程中纳米钨的变形失效过程和微结构演化进行了表征分析，从而揭示孪晶间距对纳米钨力学性能影响微观机理。结果表明：孪晶钨变形过程中出现的相变、孪晶界的变形以及去孪晶化的现象会改变孪晶钨中裂纹的扩展方式，提高孪晶界的变形能力；而随着孪晶间距的减小即孪晶密度的增加，可变形的孪晶界增多，导致纳米孪晶钨的断裂应变增加。由于孪晶界中存在能量较高的相互作用的特殊三原子结构使纳米钨中更容易出现晶体缺陷，缺陷会在拉伸载荷作用下快速形成裂纹，导致晶体断裂失效，严重降低了纳米钨的屈服强度。此外，孪晶界的存在显著降低了几何必须位错的数量同时阻碍了位错的滑移运动，位错难以发射和运动，从而导致塑性变差。

关键词：钨；纳米孪晶界；孪晶距；位错；分子动力学

文章编号：1004-0609(2021)-08-2136-10　　     中图分类号：TG147　　     文献标志码：A

引文格式：薛克敏, 张勇强, 王路生, 等. 孪晶距对纳米钨力学性能影响的分子动力学模拟[J]. 中国有色金属学报, 2021, 31(8): 2136-2145. DOI: 10.11817/j.ysxb.1004.0609.2021-40035

XUE Ke-min, ZHANG Yong-qiang, WANG Lu-sheng, et al. Molecular dynamics simulation of effect of twin boundaries spacing on mechanical properties of nano-tungsten[J]. The Chinese Journal of Nonferrous Metals, 2021, 31(8): 2136-2145. DOI: 10.11817/j.ysxb.1004.0609.2021-40035

钨(W)具有高熔点、高密度、高硬度、高模量、低热膨胀系数、耐磨及耐腐蚀等良好的物理、化学和机械性能，被广泛应用于航空航天、武器装备、核工业等众多领域，是国际热核聚变反应堆(ITER)包层的重要候选材料^[1-3]。由于钨熔点较高，工业上通常采用粉末冶金的方法进行制备。烧结钨中存在大量的孔洞和杂质，导致其塑性变形能力较差，严重影响其成形性和热性能^[4-6]。同时，粗晶烧结钨存在着严重的低温脆性和再结晶脆性等脆化问题^[7]，严重制约了纯钨的加工和应用。采用大塑性变形(SPD)技术可以在不改变其化学成分的情况下提高钨基材料的力学性能^[8-9]。本团队在采用大塑性变形工艺来改变纯钨的性能时，常常可以在变形后的试样中观察到孪晶的存在。

孪晶界作为一种特殊的大角度晶界，广泛地存在于各种常用的金属材料当中。BEAVEN等^[10]采用FIM-TEM(Field ion microscopy and transmission electron microscopy)测量方法首次观察到存在于金属钨中的孪晶界，完整地分析了孪晶界处存在的缺陷结构。MIKHAILOVSKIJ等^[11]、WENSKY等^[12]和KRASKO^[13]分别利用分子静态模拟方法研究了晶体钨中孪晶界的原子排布方式，其提出的ω相“三明治”结构几乎完全解释了钨中孪晶界的原子构型，即孪晶界面附近的交替原子面可以合并形成密排六方结构的原子面。传统的固溶强化、第二相强化、形变强化等都是向晶体内引入各种缺陷，使金属的强度增加的强化机制，但随着缺陷的增加，位错滑移运动变得困难，最终都会伴随着塑韧性的下降^[14-15]。而纳米孪晶界强化作为一种新型强化机制则不存在这种问题。有研究表明^[17]，向金属中引入孪晶界能够在增加金属强度的同时，保持甚至提高了金属的塑性。XU等^[17]和WANG等^[18]研究发现，纳米级相干孪晶界(CTB)显著地改变了金属材料的力学和电学性质，含有CTB的试样在受拉伸载荷时屈服强度不随相干孪晶间距(CTBs)变化，而在受压缩载荷时由于相干孪晶界和裂纹的相互作用导致屈服强度随CTBs的减小而增大。

分子动力学所研究的尺度是纳米级的，能够直观地展现晶体的微观缺陷和晶体结构的演变过程，因此利用分子动力学模拟的方法来研究孪晶间距对于纳米钨力学性能及变形机理的影响更有优势。周昊飞等^[19]利用分子动力学方法研究了梯度纳米孪晶铜在拉伸载荷下的变形及微观演化过程，证明孪晶的存在可以提高铜的韧性，随着孪晶密度的增加，孪晶铜的强度和硬度也有明显提高。许天旱等^[20]利用分子动力学方法对不同孪晶距的纳米铁进行单轴拉伸模拟，发现弹性模量和屈服强度都随孪晶距的增加而增加，且单晶铁的屈服强度最高。

虽然已有学者对纳米孪晶材料展开了研究，但对于孪晶的研究对象主要集中在面心立方结构(FCC)DE1和密排六方结构(HCP)的金属^[21-22]，关于体心立方结构(BCC)金属中孪晶强化机制的研究则相对较少。对于BCC晶体中孪晶对纳米金属材料形变的影响及机理仍没有确定的结论。本文利用分子动力学方法研究了体心立方结构纳米孪晶钨在单轴拉伸载荷作用下的变形及失效的影响，以期对纳米孪晶钨在拉伸载荷下的微观变形机理提供理论参考。

1  分子动力学建模过程

1.1  纳米孪晶钨原子模型

为了研究孪晶界间距对于纳米钨在拉伸载荷作用下的力学性能和微观变形影响机理，建立了不同孪晶距λ的分子动力学模型，λ的范围从1.09 nm到8.2 nm^{[17, 19-20]}。含有孪晶间距(Twin boundary spacing, TBS)为2.73 nm的模型如图1所示。纳米钨的单胞结构为体心立方结构，晶格参数为a=b=c=3.165 ，α、β和γ为90°。模型的总体尺寸为L_a=19.4 nm，L_b=16.4 nm，L_c=13.4 nm。模型中的原子数量为248200。相邻两层的晶体在x、y、z的晶向分别为、[111]、和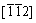、[111]、。

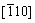1.2  势函数及边界条件设置

图1  孪晶距λ为2.73 nm的分子动力学模型

Fig. 1  Molecular dynamics model of twin boundary spacing λ=2.73 nm

本文用LAMMPS (Large-scale atom/scaler massively parallel simulation)^[23-24]软件进行分子动力学模拟。LAMMPS模拟软件计算中势函数的选择尤为重要，对于大多数金属而言，嵌入势(Embedded atomic method，EAM)势函数运用的最多^[25-27]。EAM势方法中把每个原子当作是镶嵌在余下集体中的个体，通过一系列函数描述该个体与整体的力学关系，体系的总能描述为镶嵌能和相互作用势能之和^[28]。根据嵌入原子势的定义，系统的总能(U)可以表示为

               (1)

式中：右边第一项F_i是嵌入能，第二项是对势项；是所有其他原子的核外电子在第i个原子处产生的电子云密度之和，它可以表示为

                           (2)

式中：是第j个原子的核外电子在第i个原子处的电荷密度。

本模拟为了描述W-W之间的相互作用势，采用ZHOU等^[29]改进的EAM势，该势函数已经广泛应用于纳米钨的拉伸、压缩等力学性能的研究^{[1, 17, 25, 30]}。

采用Verlet-velocity方法^[31]描述原子坐标和运动轨迹的牛顿方程。整个模拟分为两部分进行，首先在NVE系综下对模型充分弛豫使结构达到能量最小构型，时间步长为0.001 ps，驰豫时间为40 ps。在弛豫完成后，整个模拟过程在NVT系综下进行拉伸模拟，整个体系的温度设置为300 K，将所有边界设置为循环周期性边界，每1000 步输出原子坐标、温度、势能和动能等信息。通过键对分析技术(Common neighbor analysis，CNA)和位错分析法(Dislocation analysis，DXA)来表征原子内部结构的变化^[32]。模拟通过LAMMPS开源软件编程进行计算，采用OVITO后处理软件进行可视化分析^[33]。

2  结果与讨论

2.1  孪晶间距对钨力学性能的影响

常温条件下，钨的拉伸应力-应变曲线能够很好地反应晶体的拉伸力学性能，通过对模型进行拉伸分子动力学模拟可以得到不同孪晶距纳米钨和单晶钨的应力-应变曲线和弹性模量曲线。图2所示为单晶钨和不同TBS孪晶钨在单轴拉伸载荷下的力学性能。图2(a)所示为300 K下不同TBS孪晶钨和单晶钨在受Y轴方向单轴拉伸载荷的应力-应变曲线，图2(b)所示为其弹性模量曲线。从图2看出：1) 单晶钨和孪晶钨的失效方式都是脆性断裂，单晶钨的失效应变为17%，孪晶钨的失效应变随着TBS的减小而增大，但都远远小于单晶钨。2) 孪晶钨中λ=1.09 nm时失效应变最大，孪晶钨的失效应变随TBS的增大而减小，但当TBS达到5.46 nm时孪晶钨的失效应变就不再增加或者增加的速度非常缓慢；3) 孪晶钨的屈服强度为28 GPa，也远远小于单晶钨，孪晶钨的屈服强度与TBS的大小几乎无关。这与XU等^[17]对纳米孪晶柱的研究有相似的结果；不同的是在他们的研究中孪晶间距为1 nm左右时，孪晶钨的屈服强度更低且出现了应变硬化过程，表现出与其他孪晶钨不一样的变形过程。4) 孪晶钨的弹性模量随着TBS的增大而增大且逐渐趋近于单晶钨，当λ＜3.28 nm时弹性模量随TBS增大而增大的速率较快。根据CHEN等^[34]的研究可知，相邻波动孪晶界的相互作用会增加孪晶界的能量起伏，且相邻孪晶界之间存在大小为1/λ²的熵力，此相互作用力会改变孪晶界的形态。当λ＞3.28 nm时弹性模量随TBS增加而增加的速率减小，甚至当λ达到5.46 nm后，孪晶钨的弹性模量不再随孪晶距的增加而增加，此时相邻孪晶界之间的相互作用较小。

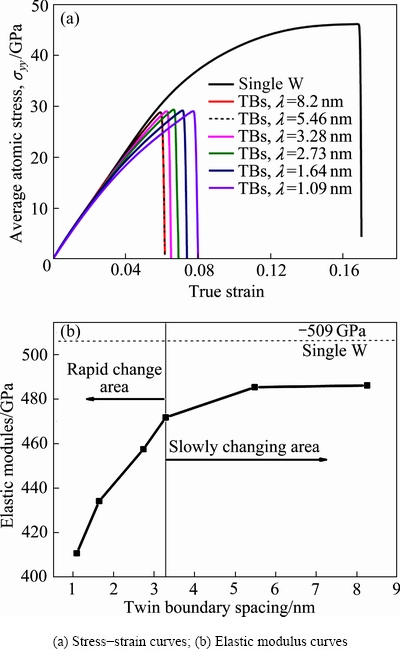
图2  单晶钨和不同TBS孪晶钨在单轴拉伸载荷下的应力-应变曲线

Fig. 2  Stress-strain curves of single crystal and twin tungsten with different TBS under uniaxial tension

2.2  不同孪晶距纳米钨拉伸变形失效过程的晶体微观结构

图3所示为单晶钨和不同TBS的孪晶钨在受单轴拉伸载荷下的变形失效过程。图3(a)所示为单晶钨拉伸变形失效过程。当单晶钨的应变达到16.9%时，在晶体内部的不同位置同时开始出现一些空位缺陷。当应变达到16.95%时，空位缺陷都沿着[210]方向扩展成为裂纹，且在裂纹的附近出现了少量的密排六方(HCP)晶格的钨。随着应变进一步增加到17%时，裂纹进一步扩展，且裂纹与裂纹之间相互平行。与此同时，在裂纹扩展的方向上和裂纹附近出现了更多的相变，同时出现了FCC(图中绿色原子)和HCP(图中红色原子)晶格的钨。当应变达到17.05%时，裂纹进一步扩大使单晶钨彻底失效，此时有较多的BCC结构发生相变产生FCC结构的纳米钨。可以看出单晶钨的变形是由晶体缺陷引发的裂纹在拉伸载荷的作用下进一步扩展，并伴随着裂纹尖端相变的发生，最终达到失效。

图3  单晶钨和不同TBS孪晶钨拉伸变形失效过程图

Fig. 3  Tensile deformation failure processes of single crystal tungsten and twin tungsten with different TBS

图3(b)所示为TBS为1.09 nm的孪晶钨拉伸变形失效过程。当应变达到7.85%时，孪晶界处开始出现裂纹；当应变达到7.9%时，裂纹开始增多，之前出现的裂纹开始沿着平行于孪晶界的(100)方向扩展，同时在裂纹扩展的方向上有极少量的钨原子由BCC晶格排布方式转化成了FCC晶格；当应变达到8%时，之前扩展到一定规模的裂纹保存下来并进一步扩展，而一些较小的裂纹出现了“愈合”现象，在原本形成小裂纹的位置处出现了去孪晶化(Detwinning)现象；当应变进一步增加到8.05%时，保存下来的大裂纹进一步扩展使孪晶钨彻底失效，在失效部位也出现了相变生成HCP晶胞，而此前出现的去孪晶化现象也得到进一步发展。

图3(c)所示为TBS为2.73 nm的孪晶钨拉伸变形失效过程。当应变达到6.8%时，在不同的孪晶界上出现了4条裂纹，两两分布在同一条孪晶界上，在孪晶界Ⅰ上出现的裂纹长度大于孪晶界Ⅱ的裂纹。在应变率达到6.85%时，随着裂纹的进一步扩展，由于未失效部分仍然受到拉伸载荷作用，相邻的孪晶界因此受到局部的拉伸载荷作用，从而出现了稍许的剪切弯曲变形。在应变达到6.9%时，孪晶界Ⅱ上的裂纹扩展成了更大的裂纹，而孪晶界Ⅰ上的裂纹也出现了图3(b)中的“愈合”现象，虽然孪晶界没有发生退化，但也没有恢复到最初的形态，且在裂纹扩展的方向上有少量的钨原子由BCC晶格转换成了FCC晶格。当应变率达到7%时，裂纹的扩展使孪晶钨彻底地失效，断口非常的平整，在最后断裂的部位有残留的穿晶位错。这种现象在其他孪晶距的纳米钨中也出现了，且都出现在快要失效断裂的时候，出现的位置也十分相似，都出现在最终失效位置的附近，可能是上文中提到的剪切弯曲变形导致的剪切应力作为位错形核、滑移的驱动力。

图3(d)所示为TBS为5.48 nm的孪晶钨拉伸变形失效过程。其变形失效过程非常简单，在应变达到6.05%时出现裂纹，裂纹沿着平行于晶界的方向一直扩展到失效，其失效应变只有6.2%。失效过程中没有出现相变，甚至没有出现多余的裂纹。

从上面的分析可以看出，单晶钨的裂纹扩展方向为(210)，而孪晶钨中裂纹的扩展方向平行于孪晶界；且单晶钨中裂纹出现的位置没有规律，而孪晶钨中所有的裂纹都出现在孪晶界中。单晶钨变形失效过程中出现了较多的相变，主要以BCC转变为FCC为主。在孪晶钨中，相变随着TBS的增加而减少，TBS较小的孪晶钨在变形失效的过程中还出现了孪晶界的变形和去孪晶现象，且孪晶距越小孪晶界的变形和去孪晶化越多，孪晶钨的断裂应变也随之增加。可以看出，在拉伸失效过程中，发生在孪晶钨基体中的相变、孪晶界的变形以及去孪晶化的现象都有效地增加孪晶钨的失效应变。其中相变多出现在裂纹扩展的尖端，对于裂纹的形貌和裂纹扩展的方向有一定的影响。孪晶界的变形和去孪晶化导致基体在拉伸过程中受到了一定的剪切应力，使其在失效过程中出现穿晶位错，改变了裂纹的形状，减缓了裂纹扩展的速度，从而提高了孪晶钨的失效应变。

图4所示为单晶钨和不同孪晶钨拉伸变形过程中不同应变下的原子力场分布图，它能反映出变形过程中单个原子受到整体所施加给它的力。如图4(a)所示，单晶钨在拉伸前和拉伸过程中原子力场的分布非常均匀，且随着应变的增加而增加，直到出现裂纹时，在裂纹两边的原子所受到的力开始降低并逐渐减小到0 GPa附近。

从图4(b)~(d)可以看出，孪晶钨在应变为0%时，位于孪晶界处的原子就受到了较大相互作用力。通过放大的原子细节图可以看到在孪晶界中心关于{010}晶面对称的3个原子中，一个原子受到较大的拉应力(图中橙色原子)，另外两个原子则受到较大的压应力(图中蓝色原子)。这3个原子内部必然存在一定的相互作用力，而这样的三原子结构存在于整条孪晶界中，因此可以认为孪晶界中存在较大的内应力，即孪晶界中有较高的晶界储存能。当对整个试样施加拉伸载荷时，孪晶界处由于能量较高，这里的原子容易挣脱晶体的束缚，形成空位和间隙原子等点缺陷；多个点缺陷同时出现在孪晶界上，最终扩展成断裂裂纹。这很好地解释了孪晶钨的脆性以及其失效应变远远小于单晶钨的现象。同时，这样的三原子结构重复排列在孪晶界中，使孪晶界具有很高的晶界能，这为变形后期位错的形核与滑移提供了能量，使位错优先于晶内形核。

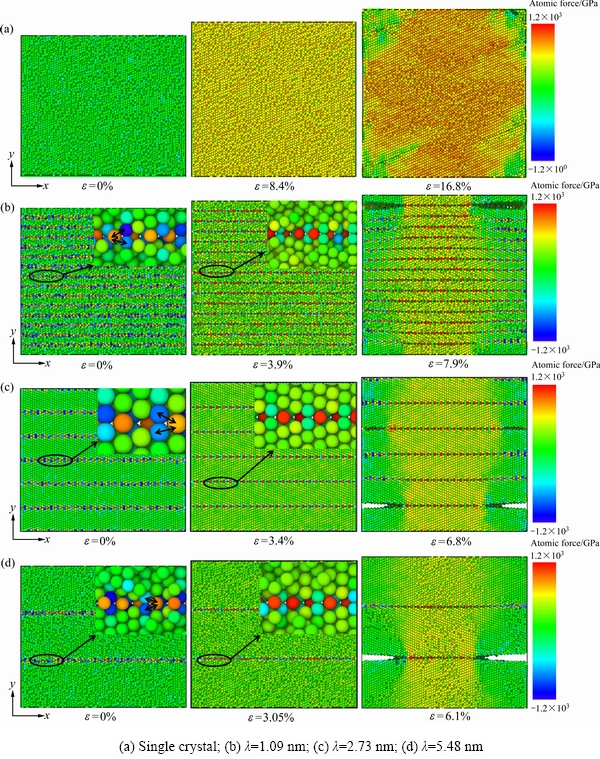
图4  单晶钨和不同TBS孪晶钨拉伸变形过程中不同应变下的原子力分布图

Fig. 4  Atomic force distribution of single crystal tungsten and twin tungsten with different TBS under different strain during tensile deformation

2.3  位错密度对于孪晶钨力学性能的影响

位错对于晶体受拉伸载荷时的力学性能有非常大的影响^[35]。因此，为了研究位错对单晶钨和不同TBS的孪晶钨在受单轴拉伸载荷时的影响，利用DXA方法对其变形失效过程中的位错线长度进行了统计。位错的统计是从位错的第一次出现到试样完全失效的过程。图5所示为单晶钨和孪晶钨在拉伸变形过程中位错线长度的变化。图5(a)所示为单晶钨在拉伸变形过程中位错线的变化，可以看出在形变过程中，产生最多的是1/2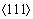全位错。随着拉伸应变从16.7%增加到16.8%，晶体内部位错形核长大的速度远远高于位错湮灭的速度，1/2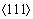全位错在很短的时间内快速增长到峰值，同时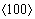位错也在快速增加，此时晶体内部的位错趋向于缠结和堆积，此时的应力应变曲线也趋于平滑。当1/2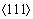位错和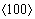位错都达到峰值后，位错的缠结和堆积也达到最大，产生应变硬化^[36-37]，最终导致材料的断裂失效。

由图5(b)~(d)可以看出，在孪晶钨中，1/2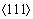位错是形变过程中出现的主要位错，TBS为2.73 nm的孪晶钨在拉伸形变过程中出现的1/2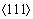位错线长度最小，为所有试样变形过程中1/2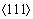位错线长度的极小值。在所有孪晶钨中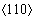位错和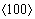位错表现出此起彼伏、相互交替出现的规律。相较于孪晶钨，单晶钨中1/2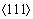位错线和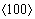位错线的长度都要比孪晶钨大一个数量级。这是因为孪晶钨内的位错从孪晶界处形核，然后向晶内滑移生长，当滑移到另一条孪晶界处时位错的运动受阻；单晶钨中位错的滑移运动则不存在这样的问题，直到位错滑移到出现相互作用的时候才开始停止生长。

3  结论

1) 孪晶钨的弹性模量随着孪晶距的增加而增加且逐渐趋近于单晶钨，其增加的速度在TBS小于2.73 nm时较快，在TBS大于3.28 nm后减缓，其主要原因是相邻孪晶界之间的相互作用导致孪晶界的能量起伏。

2) 孪晶钨的特征变形行为主要是由集中在孪晶界处的变形、开裂、相变和去孪晶化现象组成，因此纳米孪晶钨的屈服强度主要取决于孪晶界的抗变形能力。孪晶界的变形和去孪晶化导致基体中出现穿晶位错，改变了裂纹的扩展方式从而增加了孪晶界的变形能力，而随着孪晶界密度的增加可变形的孪晶界增加，孪晶钨的失效应变增加。

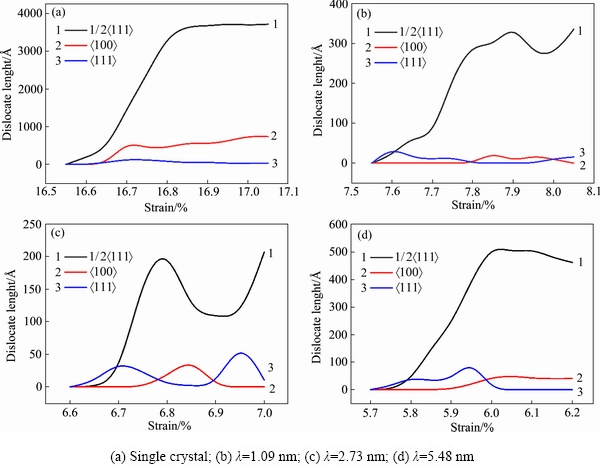
图5  单晶钨和不同孪晶钨拉伸变形过程中位错线的长度变化曲线

Fig. 5  Variation curves of dislocation line length of single crystal tungsten and different twin tungsten during tensile deformation

3) 由于孪晶界中存在能量较高的相互作用的特殊三原子结构，其中心原子存在较大的相互作用而达到一种能量较高的平衡状态，使其在拉伸载荷下很容易被破坏而形成点缺陷，当一条孪晶界中存在较多点缺陷时就容易形成裂纹，并在拉伸载荷的作用下扩展最终导致晶体出现断裂失效。

4) 由于孪晶界的存在，位错在晶体内部滑移时会受到孪晶界的阻碍而停止生长，不会出现单晶钨中位错相互缠结形成应变硬化的现象，导致孪晶钨的屈服强度远小于单晶钨。

REFERENCES

[1] MA Bin, RAO Qiu-hua, HE Yue-hui. Effect of crystal orientation on tensile mechanical properties of single-crystal tungsten nanowire[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(9):2904-2910.

[2] 李 萍, 华雅玲, 林 泉, 等. 纯钨高压扭转组织与性能的微观尺度分析[J]. 稀有金属材料与工程, 2019, 48(7): 2220-2224.

LI Ping, HUA Ya-ling, LIN Quan, et al. Microstructure evolution and micro-mechanical properties of pure tungsten during high pressure torsion[J]. Rare Metal Materials and Engineering, 2019, 48(7): 2220-2224.

[3] 陶银龙, 方一平, 王珍珍, 等. 新形势下我国钨产业发展方向探讨[J]. 中国矿业, 2015, 24(1): 15-19, 51.

TAO Ying-long, FANG Yi-ping, WANG Zhen-zhen, et al. Discussion on the development of tungsten industry under the new situation in China[J]. China Mining Magazine, 2015, 24(1): 15-19, 51.

[4] CHU Ke, JIA Cheng-chang, LIANG Xue-bing, et al. Effect of powder mixing process on the microstructure and thermal conductivity of Al/diamond composites fabricated by spark plasma sintering[J]. Rare Metals, 2010, 29(1): 86-91.

[5] CHOI J, SUNG H M, ROH K B, et al. Fabrication of sintered tungsten by spark plasma sintering and investigation of thermal stability[J]. International Journal of Refractory Metals and Hard Materials, 2017, 69: 164-169.

[6] LI Xiao-qiang, HU Ke, QU Sheng-guan, et al. 93W-5.6Ni-1.4Fe heavy alloys with enhanced performance prepared by cyclic spark plasma sintering[J]. Materials Science and Engineering A, 2014, 599: 233-241.

[7] WEI Q, JIAO T, RAMESH K T, et al. Mechanical behavior and dynamic failure of high-strength ultrafine grained tungsten under uniaxial compression[J]. Acta Materialia, 2005, 54(1): 77-87.

[8] REISER J, RIETH M, DAFFEMER B, et al. Tungsten foil laminate for structural divertor applications—Basics and outlook[J]. Journal of Nuclear Materials, 2012, 423(1/3): 1-8.

[9] MATHAUDHU S N, DEROSSET A J, HARTWIG K T, et al. Microstructures and recrystallization behavior of severely hot-deformed tungsten[J]. Materials Science and Engineering A, 2008, 503(1): 28-31.

[10] BEAVEN P A, SMITH D A, MILLER M K, SMITH G D W. Combined FIM/TEM determination of the structure of an incoherent twin boundary in tungsten[J]. Philosophical Magazine A, 1981, 43(5): 1063-1070.

[11] MIKHAILOVSKIJ I M,WANDERKA N, KSENOFONTOV V A, et al. The ω structure of the lateral twin boundary in tungsten[J]. Philosophical Magazine Letters, 2007, 87(10): 743-750.

[12] WENSKY D A, WENSKY A K. Electronic structure of the tungsten pentacarbonylamine molecules[J]. Spectrochimica Acta Part A Molecular Spectroscopy, 1975, 31(1): 23-28.

[13] KRASKO G L. Effect of impurities on the electronic structure of grain boundaries and intergranular cohesion in tungsten[J]. International Journal of Refractory Metals and Hard Materials, 1993, 12(5): 251-260.

[14] 王玉金, 宋桂明, 周 玉, 等. 合金元素及第二相对钨的影响[J]. 宇航材料工艺, 1998(6): 13-15.

WANG Yu-jin, SONG Gui-min, ZHOU Yu, et al. Effect of alloying elements and second phase on tungsten[J]. Aerospace Materials and Technology, 1998(6): 13-15.

[15] ZHANG Zhao-hui, WANG Fu-chi. Research on the deformation strengthening mechanism of a tungsten heavy alloy by hydrostatic extrusion[J]. International Journal of Refractory Metals and Hard Materials, 2001, 19(3): 177-182.

[16] LI J, ZHANGJ Y, LIU G, et al. Using the room temperature creep to strengthen nanotwinned Ni: The scaling behavior between the twin thickness and the grain size[J]. Materials Today Nano, 2020, 11: 100086.

[17] XU S, CHAVOSHI S Z, SU Y. Deformation mechanisms in nanotwinned tungsten nanopillars: Effects of coherent twin boundary spacing[J]. Physica Status Solidi (RRL)–Rapid Research Letters, 2018, 12: 1700399.

[18] WANG Yong, YU Wei-dong, WANG Fu-mei. Strand-spacing dependency on the tensile response of tri-component elastic-conductive composite yarns[J]. Textile Research Journal, 2018: 004051751876715.

[19] 周昊飞, 曲绍兴. 利用分子动力学研究梯度纳米孪晶Cu的微观变形机理[J]. 金属学报, 2014, 50(2): 226-230.

ZHOU Hao-fei, QU Shao-xing. Investgation of atomistic deformation mechanism of gradient nanotwinned copper using molecular dynamics simulation method[J]. Acta Metallurgica Sinica, 2014, 50(2): 226-230.

[20] 许天旱, 何 松. 孪晶界对α铁力学性能影响的模拟研究[J]. 航空材料学报, 2017, 37(1): 73-79.

XU Tian-han, HE Song. Simulation of effect of twin boundary on mechanical property of α-Fe[J]. Journal of Aeronautical Materials, 2017, 37(1): 73-79.

[21] 李 亨, 刘 钊, 张 真, 等. 镁合金中{1012}、{1011}两种孪晶界面的可动性比较[J]. 中国有色金属学报, 2019, 29(3): 508-516.

LI Heng, LIU Zhao, ZHANG Zen, et al. Mobility comparison of twin interfaces between {1012} and {1011} for magnesium alloy[J]. The Chinese Journal of Nonferrous Metals, 2019, 29(3): 508-516.

[22] 宋广胜, 牛嘉维, 张士宏, 等. 镁合金棒材扭转变形的孪晶机制[J]. 中国有色金属学报, 2020, 30(7): 1574-1583.

SONG Guang-sheng, NIU Jia-wei, ZHANG Shi-hong, et al. Twinning mechanism of magnesium alloy rod torsion[J]. The Chinese Journal of Nonferrous Metals, 2020, 30(7): 1574-1583.

[23] 虞 超, 杨小渝, 赵旭山, 等. 一种集成LAMMPS分子动力学软件的参数描述方法和规范[J]. 科研信息化技术与应用, 2018, 9(4): 3-14.

YU Chao, YANG Xiao-yu, ZHAO Xu-shan, et al. A parameter description method and specification for integrated LAMMPS molecular dynamics software[J]. E-science Technology and Application, 2018, 9(4):3-14.

[24] SAINATH G, CHOUDHARY B K, JAYAKUMAR T. Molecular dynamics simulation studies on the size dependent tensile deformation and fracture behaviour of body centred cubic iron nanowires[J]. Computational Materials Science, 2015, 104: 76-83.

[25] 李芳镖, 高 宁, 李奕鹏, 等. 分子动力学研究He对钨Σ3{112}对称晶界拉伸性能的影响[J]. 材料热处理学报, 2019, 40(8): 96-104.

LI Fang-biao, GAO Ning, LI Yi-peng, et al. Effect of helium on tensile properties of tungsten Σ3{112} symmetrical grain boundary studied by molecular dynamics[J]. Transactions of Materials and Heat Treatment, 2019, 40(8): 96-104.

[26] 李源才, 江五贵, 周 宇. 单晶/多晶镍复合体剪切过程分子动力学模拟[J]. 中国有色金属学报, 2020, 30(8): 1837-1845.

LI Yuan-cai, JIANG Wu-gui, ZHOU Yu. Molecular dynamics simulation on shear mechanical properties of single crystal/polycrystalline Ni composites[J]. The Chinese Journal of Nonferrous Metals, 2020, 30(8): 1837-1845.

[27] 刘晓波, 熊 震, 方 洲, 等. Al₂Cu拉伸变形的分子动力学模拟[J]. 中国有色金属学报, 2018, 28(9): 1746-1754.

LIU Xiao-bo, XIONG Zhen, FANG Zhou, et al. Molecular dynamics simulation of tensile deformation of Al₂Cu[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(9): 1746-1754.

[28] 刘 星, 时靖谊, 彭 蕾. α-Fe中氦泡阻碍位错移动硬化的分子动力学研究[J]. 原子与分子物理学报, 2018, 35(6): 1029-1036.

LIU Xing, SHI Jing-yi, PENG Lei. Molecular dynamics study of hardening induced by helium bubbles impeding edge dislocation motion in α-Fe[J]. Journal of Atomic and Molecular Physics, 2018, 35(6): 1029-1036.

[29] ZHOU X W, WADLEY H N G, JOHNSON R A, et al. Atomic scale structure of sputtered metal multilayers[J]. Acta Materialia, 2001, 49(19): 4005-4015.

[30] SHU X T, XIAO S F, DENG H Q, et al. Atomistic simulation of crack propagation in single crystal tungsten under cyclic loading[J]. Journal of Materials Research, 2017, 32(8): 1474-1483.

[31] SWOPE W C, ANDERSEN H C, BERENS P H, et al. A computer simulation method for the calculation of equilibrium constants for the formation of physical clusters of molecules: Application to small water clusters[J]. Journal of Chemical Physics, 1982, 76(1): 637-649.

[32] DING J, WANG Lu-sheng, SONG Kun, et al. Molecular dynamics simulation of crack propagation in single-crystal aluminum plate with central cracks[J]. Journal of Nanomaterials, 2017, 2017: 1-12.

[33] STUKOWSHI A. Visualization and analysis of atomistic simulation data with OVITO—The Open Visualization Tool[J]. Modelling and Simulation in Materials Science and Engineering, 2010, 18(1): 2154-2162.

[34] CHEN D, KULKARNI Y. Entropic interaction between fluctuating twin boundaries[J]. Journal of the Mechanics and Physics of Solids, 2015, 84: 59-71.

[35] CAO Yang, NI Song, LIAO Xiao-zhou, et al. Structural evolutions of metallic materials processed by severe plastic deformation[J]. Materials Science and Engineering R, 2018, 133: 1-59.

[36] HUANG Ling, LI Qing-jie, SHAN Zhi-wei, et al. A new regime for mechanical annealing and strong sample-size strengthening in body centred cubic molybdenum[J]. Nature Communications, 2011, 2: 547.

[37] GREER J R, WEINBERGER C R, CAI W. Comparing the strength of f.c.c. and b.c.c. sub-micrometer pillars: Compression experiments and dislocation dynamics simulations[J]. Materials Science and Engineering A, 2007, 493(1/2): 21-25.

Molecular dynamics simulation of effect of twin boundaries spacing on mechanical properties of nano-tungsten

XUE Ke-min, ZHANG Yong-qiang, WANG Lu-sheng, YAN Si-liang, LI Ping

(School of Materials Science and Engineering, Hefei University of Technology, Hefei 230009, China)

Abstract: In order to study the effect of twin boundaries spacing on the mechanical properties and deformation mechanism of nano-tungsten, uniaxial tensile simulation of twin tungsten with different twin boundaries spacing was carried out by molecular dynamics. The deformation failure process and microstructure evolution of nano-tungsten during tension were characterized and analyzed by using common neighbor analysis(CNA) and dislocation analysis method (DXA).The micro mechanism of the influence of twin boundaries spacing on the mechanical properties of nano tungsten was revealed. The results show that the phase transformation, the deformation of twin boundary and the phenomenon of de-twinning in the process of twin tungsten deformation will change the mode of crack propagation in twin tungsten and improve the deformation ability of twin boundary. With the decrease of twin boundaries spacing, that is, the increase of twin density, the number of deformable twin boundaries increases, resulting in the increase of fracture strain of nano-twin tungsten. Due to the existence of a special triatomic structure with high energy interaction in the twin boundaries, crystal defects are more likely to appear in the nano tungsten. The defects will form cracks quickly under the tensile load, resulting in the crystal fracture failure and seriously reducing the yield strength of the nano tungsten. Additionly, the existence of twin boundaries significantly reduces the number of geometric necessary dislocations and hinders the slip movement of dislocations, which makes it difficult for dislocations to emit and move, resulting in poor plasticity.

Key words: tungsten; nano twin boundary; twin distance; dislocation; molecular dynamics

Foundation item: Projects(51975175, 51675154) supported by the National Natural Science Foundation of China

Received date: 2020-08-24; Accepted date: 2020-12-03

Corresponding author: LI Ping; Tel: +86-551-62901368; E-mail: li_ping@hfut.edu.cn

(编辑  何学锋)

基金项目：国家自然科学基金资助项目(51975175，51675154)

收稿日期：2020-08-24；修订日期：2020-12-03

通信作者：李 萍，教授，博士；电话：0551-62901368；E-mail：li_ping@hfut.edu.cn