不同初拉力拉索对温度变化的敏感性分析
赵珧冰1,孙测世1,彭剑2,王连华1
(1. 湖南大学 土木工程学院,湖南 长沙,410082;
2. 湖南大学 机械与运载工程学院,湖南 长沙,410082)
摘要:为研究不同初始张拉力下拉索索力及模态频率对温度变化的敏感性,引入拉索热应力平衡状态,从理论上推导出考虑温差影响下的索力与正/反对称模态频率的方程,并利用数值方法求解该方程。研究结果表明:索力受降温的影响比受升温的影响更显著,而频率受升温与降温的影响程度取决于初始张拉力;初始张拉力存在临界值,且当初始张拉力大于该临界值时,升/降温对索力及频率影响的差别会逐渐减小,但是,一阶正对称模态频率除外;一般来说,温差的绝对值越大,索力与频率的变化越明显;在一定的初始张拉力范围内,温差绝对值虽小,但一阶正对称模态频率对温度的变化可能更加敏感;高阶正对称模态频率与反对称模态频率对温度变化的敏感性趋于一致。
关键词:拉索;温度变化;索力;频率;敏感性
中图分类号:U443.38 文献标志码:A 文章编号:1672-7207(2014)05-1680-06
Sensitivity analysis of different initial tension forces of suspended cable to temperature changes
ZHAO Yaobing1, SUN Ceshi1, PENG Jian2, WANG Lianhua1
(1. College of Civil Engineering, Hunan University, Changsha 410082, China;
2. College of Mechanical and Vehicle Engineering, Hunan University, Changsha 410082, China)
Abstract: In order to study the sensitivity of different tension forces of cables to temperature changes, the thermally stressed configuration of the cable was introduced and a set of equations governing the relationship between the cable tension forces and symmetric/anti-symmetric mode frequencies were derived when the temperature effect was considered, and then these equations were solved using numerical method. The results show that the sensitivity of cable tension force to cooling is slightly higher than that of warming, but as to mode frequencies, their sensitivity to cooling and warming largely depend on the initial tension forces of the suspended cable. And with the increase of the initial tension forces, the differences between cooling and warming become smaller. There are critical values of the initial tension forces, and when the initial tension force is larger than the critical one, the effects of warming/cooling on the cable tension forces and mode frequencies decrease, but except the first order symmetric mode frequency. Supposed that the absolute values of temperature change are much larger, the change of tension forces and frequencies becomes more significant. Nevertheless, to some extent of the cable initial tension force, the absolute value of temperature changes is smaller, but the sensitivity of the first order symmetric mode frequency to temperature changes may be more significant. Moreover, the temperature sensitivity of the higher order symmetric mode frequencies is more identical with that of anti-symmetric mode frequencies.
Key words: cable; temperature changes; cable tension force; frequencies; sensitivity
拉索极易受周围环境及运营条件的影响,特别是温度变化(昼夜温差、日照温差、季节温差和骤变温差等)是影响拉索振动特性的关键因素之一[1]。具体而言,温度变化会使拉索索力及振动频率发生改变,从而导致斜拉桥的振动特性发生变化[2-3]。已有研究表明:在结构健康监测中,由于温度的变化导致结构振动特性(频率、振型、振型曲率及模态柔度等)的改变,甚至比由于结构中等损伤或者是结构在正常荷载作用下结构特性的改变还要明显,因此,温度效应很可能淹没或者掩盖由于结构损伤导致的参数变化[4]。总而言之,将温度导致的结构振动特性变化从结构损伤识别过程中分离出来一直是研究的热门课题之一[5]。近些年来,考虑温度效应的影响,在分析结构的振动特性方面已有相关研究[6-9],而对于拉索,温度效应对拉索振动的影响早在1981年就被提出来[10],且近几年越来越受到研究者的重视[11-13]。已有拉索试验观测结果表明[14]:温度变化会明显改变拉索振动过程中的分岔现象。从工程实践的结果也可以看出[15-16]:温度变化对于拉索索力以及振动频率的影响是非常明显且较复杂。然而,在实际情况中,对于不同的拉索或者同一根拉索的不同阶段,其初始张拉力不尽相同,为此,本文作者从理论上推导考虑温差效应的拉索索力与频率的关系式[17],分析和阐述不同初始张拉力的拉索在考虑温差效应时索力和频率对于温度变化的敏感性。
1 运动方程
在如图1所示水平拉索模型中,点A为坐标原点,AB 轴方向为 x 坐标,与 AB 轴垂直的方向为 y 轴;L,d和H分别为拉索弦长、跨中垂度以及初始张拉 力。图1中拉索的3种线形分别为初始平衡状态、热应力平衡状态及热应力下线性自由振动状态。
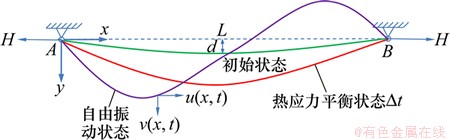
图1 拉索3种线形及其特性
Fig. 1 Three configurations of cable and its characteristics
1.1 初始平衡状态
在如图1所示的水平拉索在自重作用下,在(x, y) 点处,x和y方向的静平衡方程为
 ,
, (1)
(1)
其中:T 为沿着索长方向的初始张拉力;mg 为拉索线重力; 。
。
1.2 热应力平衡状态
假设温度发生改变,改变量为△t(△t为正表示升温,△t为负表示降温),则拉索在热应力状态下的平衡方程可以表示为
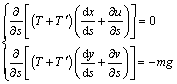 (2)
(2)
其中:u和v分别为温度变化引起的拉索x和y方向位移; 为拉索中增加的张拉力(
为拉索中增加的张拉力( )。
)。
引入温度变化△t,可以得到关于张拉力增量h的三次无量纲化方程[10]:
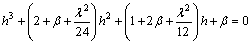 (3)
(3)
其中: ;
; ;
; ,
, 。
。
1.3 自由振动状态
线性自由振动状态下的平衡方程为:
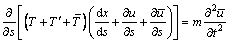 (4)
(4)
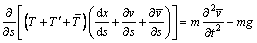 (5)
(5)
其中: 和
和 分别为拉索在x和y方向的平面运动位移;
分别为拉索在x和y方向的平面运动位移; 为由于拉索振动而增加的动拉力。
为由于拉索振动而增加的动拉力。
根据拉索振动的特点,可将其分为正对称模态与反对称模态2种情况。
(1) 反对称模态时,拉索振动频率为
 ;n=1, 2, 3, … (6)
;n=1, 2, 3, … (6)
其中: 。
。
(2) 正对称模态时,拉索频率为以下超越方程的解:
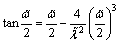 (7)
(7)
其中: 。
。
2 数值结果及分析
利用数值方法(牛顿-拉夫逊法)求解拉索频率方程(7),其中拉索物理参数为[12]:长度L=200 m,横截面面积A=7.069×10-2 m2,弹性模量E=2.0×1011 Pa,密度ρ=7.8 t/m3,拉索的热膨胀系数 =1.2×10-5 ℃,重力加速度g=9.81 m/s2。计算中,拉索初始张拉力的变化范围为[0.65×107, 5.0×107] N,则对应的Irvine参数λ2为[0.132 4, 60.041 3]。
=1.2×10-5 ℃,重力加速度g=9.81 m/s2。计算中,拉索初始张拉力的变化范围为[0.65×107, 5.0×107] N,则对应的Irvine参数λ2为[0.132 4, 60.041 3]。
为分析不同初始张拉力下(即不同Irvine参数λ2)索力及振动频率对温度的敏感程度,分别定义索力和频率的变化率为
 ;
; (8)
(8)
其中:H0和 分别表示不考虑温度变化,即当△t=0 ℃时,索力及各阶频率;H△t和
分别表示不考虑温度变化,即当△t=0 ℃时,索力及各阶频率;H△t和 分别表示温差为△t时拉索索力及其各阶频率。
分别表示温差为△t时拉索索力及其各阶频率。
图2所示为不同初始张拉力,即不同垂度的拉索在考虑温度效应时的索力变化率。从图2可以看出:温度变化对拉索索力的影响相当明显,最大幅度约为37.7%;当温差相同时,若拉索的初始张拉力不同,则索力对温度的敏感程度也是有区别的;拉索张拉力存在1个临界值(Hcr);当拉索的初始张拉力大于或者小于该临界值(Hcr)时,索力对温度变化的敏感性均会下降,且该临界值与温差相关。
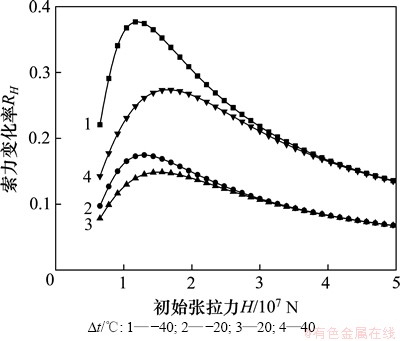
图2 初始张拉力与索力变化率的关系
Fig. 2 Relationship between initial cable tension and cable tension force variation rate
初始张拉力与索力变化率差值的关系如图3所示。从图3可见:当升温与降温程度相同(绝对值相等)时,索力受温差变化的影响程度是不对称的,且降温比升温的影响更加明显;但随着初始张拉力的不断增加,变化率的差值逐渐趋向于0。从工程的角度来说,对于初始张拉力非常大的斜拉索,绝对值相同的升温与降温过程对拉索索力的影响趋于一致。
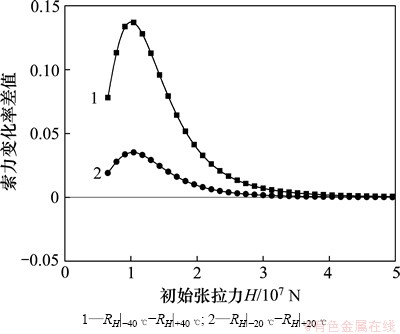
图3 初始张拉力与索力变化率差值的关系
Fig. 3 Relationship between initial cable tension and difference of cable tension force variation rate
图4~9所示为具有不同初始张拉力的拉索在考虑温度变化的影响时,前2阶反/正对称模态频率的变化情况。其中,图4和图5所示为不同初拉力的拉索的一阶反对称模态频率受温差的影响程度。比较图2和图4可知:该阶频率的变化趋势与索力的变化趋势基本一致;不同点在于当初始拉力大于一定值时(图中2根曲线的交点),该阶反对称模态频率对于升温比降温较敏感。从图5可以看出:随着初始张拉力的不断增大,绝对值相同的升温与降温过程对一阶反对称模态频率的影响仍有明显区别,相比而言,图2中并不存在该现象。
图6和图7所示为不同温度作用下一阶正对称模态频率的变化率及其差值随着初始张拉力增加的变化趋势。从图6和图7可见:总体来说,该频率受温度的影响程度与反对称模态频率相比,其幅值虽偏小,但变化非常复杂。
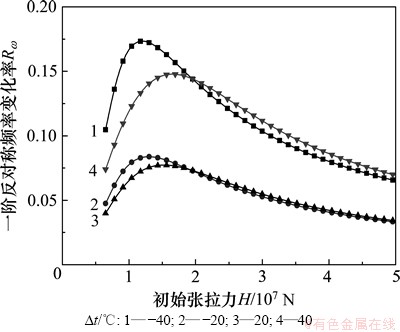
图4 初始张拉力与一阶反对称模态频率变化率的关系
Fig. 4 Relationship between initial cable tension and the first-order anti-symmetric mode frequency variation rate
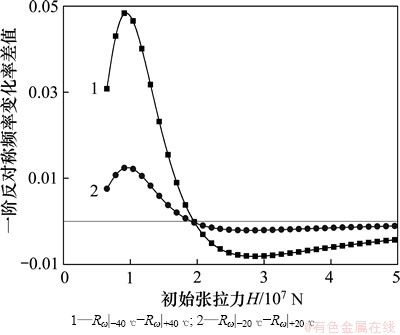
图5 初始张拉力与一阶反对称模态频率变化率差值的关系
Fig. 5 Relationship between initial cable tension and difference value of the first-order anti-symmetric mode frequency variation rate
从图6可见:随着初始张拉力的增加,该阶正对称模态频率的变化率先增大,之后减小,然后逐渐增大,最后慢慢减小;在一定范围内(图中曲线极小值附近),尽管当升温与降温的绝对值区别较大时(比如温差分别为20 ℃与40 ℃),但两者的频率变化率较接近,甚至出现当温差绝对值较小时,该阶频率的敏感程度较大的现象;在大部分范围内(极小值附近以外的范围),升温/降温的幅度越大,频率受其影响越明显。由图7可知:对于绝对值相等的升温与降温过程,频率受其影响的程度取决于拉索初始张拉力,但随着初始张拉力的不断增大,升温与降温的区别逐渐减小。
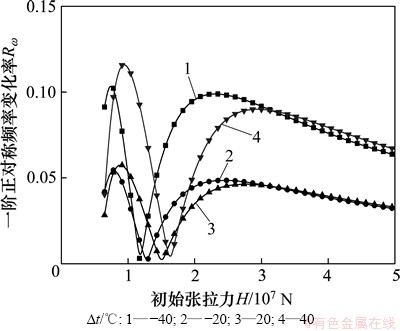
图6 初始张拉力与一阶正对称模态频率变化率的关系
Fig. 6 Relationship between initial cable tension and the first-order symmetric mode frequency variation rate
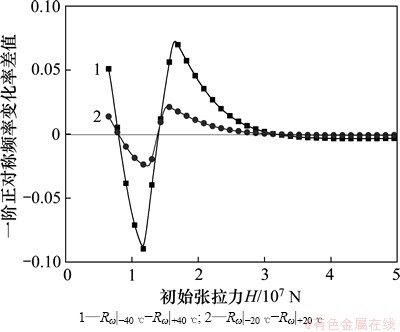
图7 初始张拉力与一阶正对称模态频率变化率差值的关系
Fig. 7 Relationship between initial cable tension and the difference value of the first-order symmetric mode frequency variation rate
图8和图9所示为不同初拉力的拉索的二阶反对称/正对称模态频率在温度影响下的变化趋势。比较图8与图4可知:一阶/二阶反对称模态频率的变化趋势基本一致;对于二阶正对称模态频率(如图9所示),其变化率的趋势与一阶正对称模态频率的变化趋势区别很大,但是,与反对称模态下的频率变化率变化趋势较接近。不同之处在于:当初始张拉力很小时(图中曲线起点附近),该阶频率变化率区别不明显。
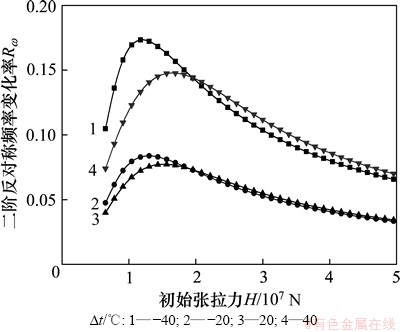
图8 初始张拉力与二阶反对称模态频率变化率的关系
Fig. 8 Relationship between initial cable tension and the second-order anti-symmetric mode frequency variation rate
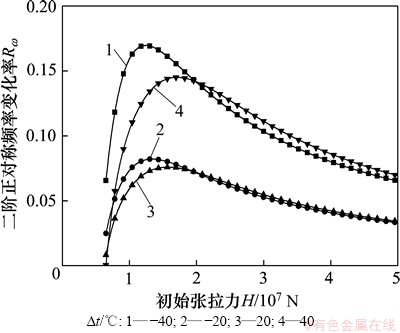
图9 初始张拉力与二阶正对称模态频率变化率的关系
Fig. 9 Relationship between initial cable tension and the second-order symmetric mode frequency variation rate
3 结论
(1) 拉索索力及其振动频率对于温度的变化均很敏感,但相比较而言,索力的敏感程度稍大;二阶及以上的正对称模态频率的变化趋势与反对称模态频率的变化趋势基本一致。
(2) 索力及频率对于升/降温的敏感程度均不对称:对于索力,在初始张拉力不大时,降温对其影响程度大于升温的影响程度,随着初始张拉力的增加,两者差别逐渐减小;但对于频率,升温与降温对频率的影响程度取决于拉索初始张拉力,即不同初拉力时,两者可能不同。
(3) 对于相同物理参数的拉索,并不是初始张拉力越大或越小,索力和频率对温度变化的敏感性越大,两者的敏感性均存在极值,且该极值与温差密切相关。
(4) 一般来说,温差绝对值越大,索力与频率的变化越明显,但是,在一定的初始张拉力范围内,尽管温差绝对值很小,但一阶正对称模态频率的变化率也可能很大。
参考文献:
[1] 邓扬, 丁幼亮, 李爱群. 环境条件影响下悬索桥模态频率变异性的定量评价[J]. 振动与冲击, 2011, 30(8): 230-236.
DENG Yang, DING Youliang, LI Aiqun. Quantitative evaluation of variability in modal frequencies of a suspension bridge under environmental conditions[J]. Journal of Vibration and Shock, 2011, 30(8): 230-236.
[2] 李顺龙, 李惠, 欧进萍, 等. 考虑温度和风速影响下的桥梁结构模态参数分析[J]. 土木工程学报, 2009, 42(4): 100-106.
LI Shunlong, LI Hui, OU Jinping, et al. Identification of modal parameters of bridges considering temperature and wind effects[J]. China Civil Engineering Journal, 2009, 42(4): 100-106.
[3] 闵志华, 孙利民, 淡丹辉. 影响斜拉桥模态参数变化的环境因素分析[J]. 振动与冲击, 2009, 28(10): 99-105.
MIN Zhihua, SUN Limin, DAN Danhui. Effect analysis of environmental factors on structural modal parameters of cable-stayed bridge[J]. Journal of Vibration and Shock, 2009, 28(10): 99-105.
[4] 李苗, 黄天立, 任伟新. 温度影响下基于主成分分析和模态柔度的结构异常检测[J]. 振动与冲击, 2011, 30(5): 83-87.
LI Miao, HUANG Tianli, REN Weixin. Structural novelty detection under temperature variation based on PCA and modal flexibility[J]. Journal of Vibration and Shock, 2011, 30(5): 83-87.
[5] Xia Y, Chen B, Weng S, et al. Temperature effect on the vibration properties of civil structures: A literature review and case studies[J]. Journal of Civil Structure Health Monitoring, 2012, 2(1): 29-46.
[6] 李世荣, 宋曦, 赵永刚. 变厚度环板在面内变温下的固有频率[J]. 工程力学, 1995, 12(1): 58-65.
LI Shirong, SONG Xi, ZHAO Yonggang. Natural frequency of the annular plates with variable thickness and subjected to a in-plane temperature rising[J]. Engineering Mechanics, 1995, 12(1): 58-65.
[7] 曲展, 陈军斌, 刘实. 井下高温对内含钻井液钻柱振动固有特性的影响分析[J]. 振动与冲击, 1998, 17(2): 75-78.
QU Zhan, CHEN Junbin, LIU Shi. Analysis of the downhole temperature affection on the drill string containing drill fluid flow[J]. Journal of Vibration and Shock, 1998, 17(2): 75-78.
[8] 杨志安, 刘鹏飞, 席晓燕. 温度场中输电线在谐扰力作用下的1/3次亚谐共振研究[J]. 工程力学, 2007, 24(8): 182-187.
YANG Zhi’an, LIU Pengfei, XI Xiaoyan. 1/3 sub-harmonic resonance of suspended cable subjected to harmonic excitation in temperature field[J]. Engineering Mechanics, 2007, 24(8): 182-187.
[9] 杨晓峰, 李晓红, 卢义玉. 岩石钻掘过程中的钻头温度分析[J]. 中南大学学报(自然科学版), 2011, 42(10): 3164-3169.
YANG Xiaofeng, LI Xiaohong, LU Yiyu. Temperature analysis of drill bit in rock drilling[J]. Journal of Central South University (Science and Technology), 2011, 42(10): 3164-3169.
[10] Irvine H M. Cable structures[M]. Cambridge, NJ: The MIT Press, 1981: 82-83.
[11] 吴晓, 杨立军, 孙晋, 等. 碳纤维材料双层索非线性自振的温度响应[J]. 西安建筑科技大学学报(自然科学版), 2008, 40(2): 155-160.
WU Xiao, YANG Lijun, SUN Jin, et al. The influence of temperature on the nonlinear free vibration of double-layer cable system with carbon fiber reinforced polymer[J]. Journal of Xi’an University of Architecture & Technology (Natural Science Edition), 2008, 40(2): 155-160.
[12] Treyssede F. Free vibrations of cables under thermal stress[J]. Journal of Sound and Vibration, 2009, 327(1/2): 1-8.
[13] Lepidi M, Gattulli V. Static and dynamic response of elastic suspended cables with thermal effects[J]. International Journal of Solids and Structures, 2012, 49(9): 1103-1116.
[14] Rega G, Alaggio R. Experimental unfolding of the nonlinear dynamics of a cable-mass suspended system around a divergence-hopf bifurcation[J]. Journal of Sound and Vibration, 2009, 322(3): 581-611.
[15] 侯俊明, 彭晓彬, 叶方才. 斜拉索索力的温度敏感性[J]. 长安大学学报(自然科学版), 2002, 22(4): 34-36.
HOU Junming, PENG Xiaobin, YE Fangcai. Temperature effect on cable’s forces controlling of cable-stayed bridge[J]. Journal of Chang’an University (Natural Science Edition), 2002, 22(4): 34-36.
[16] 蔡敏, 蔡键, 李彬, 等. 环境因素对斜拉桥斜索自振频率的影响[J]. 合肥工业大学学报(自然科学版), 1999, 22(5): 36-39.
CAI Min, CAI Jian, LI Bin, et al. Influence of the ambient conditions on the natural frequencies of cable[J]. Journal of Hefei University of Technology (Natural Science Edition), 1999, 22(5): 36-39.
[17] 赵珧冰, 孙测世, 彭剑, 等. 温度变化对拉索频率与索力的影响[J]. 应用力学学报, 2013, 30(6): 904-908.
ZHAO Yaobing, SUN Ceshi, PENG Jian, et al. Effects of temperature changes on the frequencies and tension forces of cables[J]. Chinese Journal of Applied Mechanics, 2013, 30(6): 904-908.
(编辑 陈灿华)
收稿日期:2013-05-10;修回日期:2013-07-15
基金项目:国家自然科学基金资助项目(11032004,11102063,11002030)
通信作者:王连华(1975-),男,湖南娄底人,博士,副教授,从事结构非线性动力学研究;电话:0731-88823962;E-mail: ybzhao@hnu.edu.cn