DOI: 10.11817/j.issn.1672-7207.2016.09.035

非贯通节理岩体等效强度及破坏特性

金爱兵，孙浩，孟新秋，王凯，杨振伟

(北京科技大学 土木与环境工程学院，北京，100083)

摘要：应用PFC^2D数值模拟软件，选取适当的细观力学参数，建立非贯通节理岩体试样数值模型并进行双轴试验，设置监控圆监测岩体压缩过程非贯通节理面上不同位置应力及其变化情况。以莫尔-库仑强度准则为基础，对非贯通节理的等效强度参数进行推导，提出含非贯通节理的岩体等效强度公式。建立等效岩石试样和节理岩体试样数值模型进行双轴压缩试验，对含非贯通节理岩体等效强度进行数值模拟。研究结果表明：双轴压缩过程岩桥上应力大于相同时刻节理面上的应力，且岩桥达到峰值强度时节理面并没有达到峰值强度。等效强度公式计算得到的非贯通节理岩体强度与数值模拟得到的强度比较接近，应力-应变曲线基本一致。

关键词：非贯通节理岩体；等效强度；PFC^2D；双轴试验

中图分类号：TU45          文献标志码：A         文章编号：1672-7207(2016)09-3169-08

Equivalent strength and failure behavior of intermittent jointed rock mass

JIN Aibing, SUN Hao, MENG Xinqiu, WANG Kai, YANG Zhenwei

(School of Civil and Environment Engineering, University of Science and Technology Beijing, Beijing 100083, China)

Abstract: By using the numerical simulation software PFC^2D, the appropriate micro mechanics parameters were selected, then the model of jointed rock mass specimen was established and measurement circle at different position of joint surface was set up to monitor the stress changes. Based on Mohr-coulomb strength criterion, the equivalent strength of rock mass with single intermittent joint was deduced and an equivalent conversion formula was given. Different joint penetration rate and confining pressure level were set before the model of equivalent rock and jointed rock mass specimen were established, and then the equivalent strength theory was demonstrated by biaxial tests. The results show that the stress on rock bridge is greater than the stress on joint at the same time through the whole biaxial test. The strength parameters calculated with the formula get high consistency with the parameters of numerical simulation and the stress-strain of joint rock and equivalent rock has high similarity.

Key words: intermittent jointed rock; equivalent strength; PFC^2D; biaxial test

根据发育程度及岩体强度控制程度岩体中的节理，可以分为贯通节理、遍布节理、非贯通节理(断续节理)和隐闭节理。当岩体强度和变形及破坏形式主要受断续发育的节理影响时，工程上将这样的岩体称为非贯通节理岩体^[1-2]。含有非贯通节理的岩体没有明显的贯通结构面，也不是完全连续的介质。节理化块体模型只能得到部分体现，岩桥和节理将以不同的阻抗原理共同承担荷载^[3-4]。因此，很多学者从节理面及岩桥方面对节理岩体破坏机理及力学性质作了大量的研究。如夏才初等^[5]通过非贯通人工节理的直剪试验，对剪切过程中非贯通节理岩桥力学性质弱化的力学机制进行阐述；刘远明^[6]基于岩桥力学性质弱化机制，采用带伺服系统的直剪试验仪进行试验，对非贯通节理岩体进行直剪试验，研究非贯通节理岩体的强度特性和变形特性。但室内试验通常存在耗时耗力，且不能从细观角度对岩石破坏机理进行解释的弊端。随着计算机技术的发展，数值模拟可以克服室内试验存在的缺点，逐渐成为岩石力学研究与工程计算重要而且有效的手段。基于颗粒流程序的PFC程序在建模过程中岩体由一个个细小的圆形颗粒组成，通过赋予颗粒与颗粒间的一些力学参数及黏结方式，能够很好地模拟真实岩体的力学行为，并且能从细观的角度对这些力学行为进行分析研究^[7-8]，所以得到很多学者的青睐。在节理岩体变形破坏机理方面：金爱兵等^[9]采用颗粒流数值模拟程序，建立不同节理状态的岩石试样模型，对其进行双轴试验，从岩桥长度、节理长度和倾角3个方面对断续节理影响下的岩体破裂形式和力学性质进行了数值模拟分析。刘顺桂等^[10]设计不同连通情况和法向应力的断续节理模型材料直剪试验，并采用颗粒流离散元软件PFC^2D对模型试验进行全真数值模拟，对比分析数值模拟曲线和模型试验曲线，对断续节理受剪贯通的力学机制进行研究。还有其他学者在节理岩体力学性质及变形破坏机理方面做了大量的研究，也取得了丰厚的成果^[11-15]。由这些研究成果可知：由于岩桥和贯通节理面的力学性质不同，在岩体沿非贯通节理面发生剪切破坏的过程中岩桥和贯通节理面上应力会有很大的差异。本文作者以莫尔-库仑强度准则为基础，采用PFC^2D数值模拟软对这一差异进行研究，提出含单条非贯通节理的岩体等效强度并进行验证。

1  节理岩体等效强度

1.1  贯通节理岩体等效强度

对于图1所示节理倾角为β的贯通节理岩体，在主应力σ₁和σ₃作用下，节理面上将出现正应力σ和剪应力τ。

根据库仑强度准则可得出节理面上正应力σ和剪应力τ满足式(1)：

图1  贯通节理岩体受力状态

Fig. 1  Stress state of joint rock mass

由式(1)可知：当β趋近于0或π/2时，剪应力τ趋近于0。说明节理岩体的破坏并不一定都会沿着节理面发生，只有当节理面倾角β在某一范围(β₂＜β＜β₁)时，岩体的破坏才将有可能沿着节理面发生。根据图2，由耶格尔判据^[16]可以得到β₁和β₂满足式(2)：

式中：C_j和分别为节理面内聚力和内摩擦角。

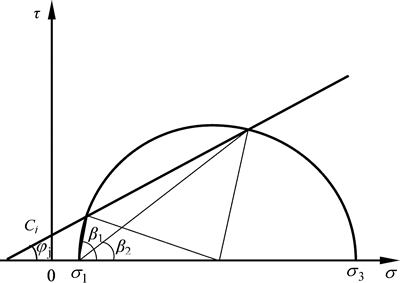
图2  节理面力学效应

Fig. 2  Mechanical effects of joint plane

综合上述分析，单条贯通节理岩体的等效强度参数选取分以下2种情况：

1) 当β＜β₂或β＞β₁时，由于此时岩体破坏贯穿节理面发生，节理岩体的等效强度近似认为是完整岩石的强度，即：φ=φ_r，C=C_r，其中，C和φ分别为节理岩体内聚力和内摩擦角；C_r和φ_r分别为岩桥的内聚力和内摩擦角。

2) 当β₂＜β＜β₁时，节理岩体的强度由节理面控制，其等效强度参数C和φ满足式(3)。

对于非贯通节理岩体，节理面由贯通部分和没有贯通的完整岩石部分(岩桥)组成，可以选择适当的折减方法将其假想成强度经过折减的贯通节理，进而可以按照上述贯通节理岩体等效强度的计算方法算出非贯通节理岩体的强度参数。目前采用的方法大多是对岩体强度参数进行简单的加权计算，即：

式中：A_j为节理贯通率；和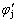分别为经过折减的贯通节理面内聚力和内摩擦角。

1.2  细观参数选取

本数值实验以某矿露天边坡砂岩室内实验数据为基础，岩体宏观力学参数如表1所示，节理剪切刚度与完整岩石剪切刚度比为0.3。采用颗粒流程序，接触模型选择平行黏结模型，建立长×宽为100 mm×50 mm的完整岩石数值模型(图3(a))。在图3(a)所示的试样模型基础上，采用JSET命令添加1条中心与岩样中心重合、倾角为60°的非贯通节理面，则建立起岩桥在中间，节理在两端的非贯通节理岩体模型(图3(b))。模型以墙体作为边界条件，1号和3号墙体伺服控制用以提供围压，2号和4号墙体指定一定速度用以对试样进行加载。

对数值模型进行计算分析前，先赋予模型一定的细观力学参数，对该细观参数条件下的试样进行数值模拟试验，得到试样的力学性质，经反复调试，当数值模拟结果与室内试验结果一致时，此时该细观参数可以应用于模拟真实岩石。

采用表2和表3中的细观力学参数建立完整砂岩模型进行单轴压缩试验，得到的岩样单轴抗压强度σ_c、弹性模量E和泊松比μ分别为11.7 MPa，14.60 GPa和0.23，与表1中所列砂岩室内试验结果十分相近。

表1  岩体室内试验力学参数

Table 1  Mechanical parameters of indoor test of rock mass

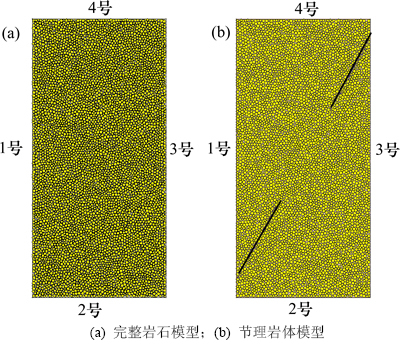
图3  岩石数值模型

Fig. 3  Numerical model of rock

根据双轴压缩试验得到的围压与最大轴向应力关系可以绘出图4。从图4可以看出：室内试验τ-σ关系曲线与PFC^2D模拟计算应力圆基本相切，近似为它的强度包络线，说明岩体数值模型的内聚力和内摩擦角与实际室内力学实验的基本相同。因此表2和表3中所列细观力学参数可以用来模拟岩体的应力-应变关系。

表2  颗粒模型细观参数

Table 2  Mesoscopic parameters of particle model

表3  平行黏结模型细观参数

Table 3  Mesoscopic parameters of parallel bond model

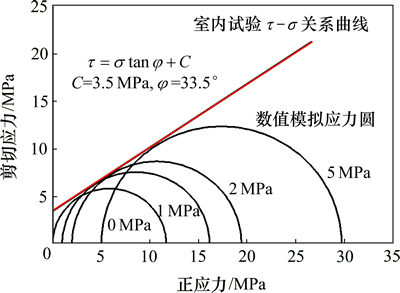
图4  细观参数调试结果

Fig. 4  Calibration result of micro mechanical parameters

同样，通过直剪实验，当数值实验得到宏观力学参数与室内试验吻合时，该细观力学参数可用。最终得到节理面细观力学参数如表4所示。

1.3  模拟实验及结果

采用以上细观参数建立非贯通节理岩体数值模型，在非贯通节理面上设置如图5所示的1~9共9个监控圆，用于记录岩体在进行双轴压缩实验过程中节理面不同位置剪应力及其变化情况。其中4~6这3个监控圆中心位于岩桥上，其余6个监控圆位于贯通部分的节理面上。

表4  节理面细观力学参数

Table 4  Mesoscopic mechanics parameters of joint plane

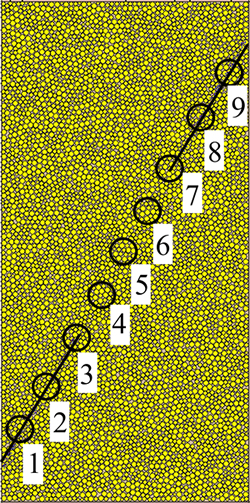
图5  监控圆

Fig. 5  Measurement circles

图6所示为不同监控圆上的剪应力情况，标号为监控圆编号。从图6可以看出：9个监控圆上剪应力分布有着明显的规律：相同时刻非贯通节理面上不同位置的颗粒所处应力状态差别很大；1) 4~6这3个监控圆上应力时刻比较接近且明显大于相同时刻其他监控圆上的应力；2号和8号监控圆，即位于2条节理面中心位置的监控圆上的应力比相同时刻其他位置的要小；1号，3号，7号和9号监控圆上应力居中。2) 4~6号曲线剪应力峰值在程序运行至30 000步附近达到；其他曲线在程序运行至33 000步附近达到。这一现象表明：岩桥在节理面被贯通破坏过程中承担较大一部分剪切破坏力，且岩桥与节理面的破坏并不同步，节理面先于岩桥达到峰值剪切强度。

图6  节理面上剪切应力分布及变化曲线

Fig. 6  Curves of shear stress distribution and change of joint surface

1.4  非贯通节理岩体等效强度

根据以上数值模拟结果，基于一定的法向应力作用下，非贯通节理平面上的抗剪强度等于该平面上节理与岩石2部分的抗剪力之和这一原则，对非贯通节理岩体等效强度参数进行修正。

即：

式中：为非贯通节理面剪切强度；k_j和k_r分别为节理面和完整岩石的剪切刚度。

整理可得：

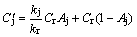
此时，根据式(7)和式(8)便可计算出等效贯通节理面的力学参数，即内摩擦角和内聚力。参照贯通节理岩体的计算方法，可以得出当节理面与最大主平面的夹角满足β₂＜β＜β₁(即，岩体沿节理面破坏)时，非贯通节理岩体的等效强度参数为

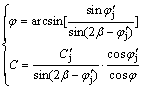
式中：和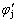分别由式(7)和(8)确定。

2  非贯通节理岩体等效强度数值模拟

围压等级设为1，2和5 MPa；通过改变岩桥和节理部分的长度可以改变贯通率，节理贯通率设为0.2，0.4和0.6。在3组围压下分别进行双轴压缩实验，得到最大轴向应力，根据莫尔强度准则进一步计算得到岩体宏观力学参数内聚力和内摩擦角。

以结构面倾角为60°的岩样为例，数值模拟计算结果及依据等效强度公式计算的结果如表5所示。

表5  内摩擦角和内聚力计算结果对比

Table 5  Comparison of calculation results for internal friction angle and cohesion

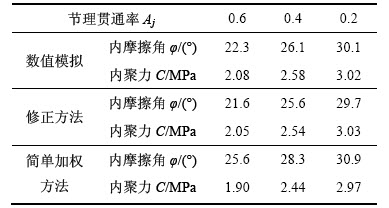
图7所示为3组节理贯通率情况下采用本文提出的改进方法计算与简单加权方法计算结果对比，在节理贯通率较小(A_j=0.2)时2种计算方法得到结果相近，区别不明显。但在贯通率较大(A_j=0.4和A_j=0.6)时，可以看出使用本文提出的修正方法计算值更接近数值模拟结果。在结构面倾角为40°和50°时，岩体同样沿结构面破坏，内聚力和内摩擦角也表现出同样的规律。

通过提出的推导公式可以计算出含有非贯通节理的岩体抗剪强度参数，即内摩擦角和内聚力；与对应节理岩体具有相同内聚力和内摩擦角的完整岩石，本文称之为等效岩石。图8所示为2 MPa围压不同节理贯通率条件下等效岩石与节理岩体双轴压缩实验应力-应变曲线。从图8可以看出：等效岩石和节理岩体的应力-应变关系曲线比较接近，峰值抗压强度相近，3组曲线节理岩体弹性模量较等效岩石的小。

图7  应力计算结果对比

Fig. 7  Comparison of calculation results for stress

图9所示为节理贯通率为0.4时的岩体分别在1，2和5 MPa围压下进行双轴压缩试验得到的应力-应变关系曲线与等效岩石的应力-应变关系曲线对比。二者具有相近的峰值强度；节理岩体的弹性模量较等效岩石的低，且随围压增高这种差距逐渐变小。

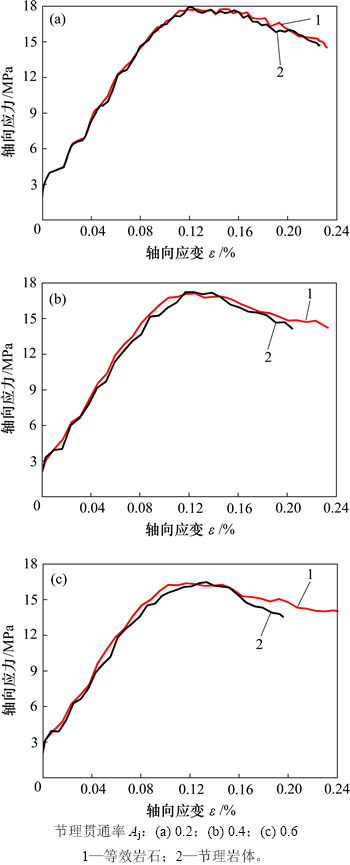
图8  围压为2 MPa时应力-应变曲线

Fig. 8  Stress-strain curves of sample under confining stress of 2 MPa

图9  不同围压等级应力-应变关系曲线

Fig. 9  Stress-strain curves of rock mass under different confining pressures

通过对比分析可知：根据非贯通节理岩体等效强度参数公式计算出的内摩擦角和内聚力与数值模拟计算得到的结果相近，误差较小。在不同围压及节理贯通率的情况下节理岩体应力-应变关系曲线与等效岩石的都比较接近，节理岩体的弹性模量较等效岩石的略小且峰后强度下降较快。总体上宏观力学性质比较接近。

3  非贯通节理面破坏特性

在上述实验的基础上，选取节理贯通率为0.6、结构面倾角为60°的岩样，在围压为2 MPa时分节理在中间和节理在两端2种情况进行压缩试验模拟，观察其内部细观裂纹的发生和发展状况。

图10(a)所示为节理面在两端的岩体模型在双轴压缩过程沿节理面破坏时内部微裂纹发展情况示意图。图10中(1)~(3)分别为程序运行到25 000，30 000和35 000步时细观裂纹的发展情况。两贯通节理面上首先出现剪切裂纹；随着试样的进一步压缩，在岩桥与贯通节理面交接地方开始出现张拉裂纹；随着程序不断运行，微裂纹不断扩展，在程序运行到30 000步左右时，整个岩样已经基本被贯通，岩体沿非贯通节理面发生破坏，形成1条非常明显的宏观裂纹；继续压缩使岩桥上出现更多的微裂纹。整个过程裂纹主要集中非贯通节理面上，岩体其他部分几乎没有裂纹的发生和发展。

图10  微裂纹发展

Fig. 10  Development of micro cracks

图11  应力应变曲线对比

Fig 11  Comparison result of stress-strain curves

图10(b)所示为节理面在中间位置的岩体模型压缩过程内部裂纹发展情况，所表现的规律与节理在两端时的相近，且通过图11可以发现：两者具有相近的应力应变关系曲线。

4  结论

1) 岩桥在节理面被贯通破坏过程中承担较大一部分剪切破坏力，且岩桥与节理面的破坏并不同步，节理面先于岩桥达到峰值剪切强度。

2) 通过对简单加权平均非贯通节理岩体抗剪强度参数进行修正，得到含单条节理的非贯通节理岩体在沿节理面发生破坏时的等效抗剪强度参数：

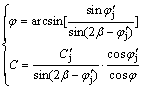
3) 修正的非贯通节理强度参数与简单加权平均法相比更接近数值模拟结果，尤其是贯通率较大时，优势更为明显。

4) 根据修正的等效岩体抗剪强度参数建立完整岩石模型，与非贯通节理岩体进行对比模拟，所获得的等效岩石应力-应变曲线与非贯通节理岩体应力-应变曲线基本一致，且具有近似的峰值强度。

5) 岩桥的破坏是非贯通节理岩体贯通破坏的关键，在岩体沿节理面破坏情况下，裂纹主要从节理与岩桥交界处发生，然后沿着岩桥不断发展，最终导致岩样破坏。

参考文献：

[1] 蔡美峰. 岩石力学与工程. 北京: 科学出版社, 2004: 84-89.

CAI Meifeng. Rock mechanics and engineering[M]. Beijing: Science Press, 2004: 84-89.

[2] 周维垣. 高等岩石力学[M]. 北京: 水利电力出版社, 1990: 53-54.

ZHOU Weiyuan. Advanced rock mechanics[M]. Beijing: Water Resources and Electric Power Press, 1990: 53-54.

[3] 刘东燕, 叶晓明, 朱凡. 断续节理岩体强度评价及承载力预测[J]. 重庆建筑大学学报, 1997, 19(2): 21-30.

LIU Dongyan, YE Xiaoming, ZHU Fan. Intermittent joint strength assessment and bearing capacity prediction[J]. Journal of Chongqing Jianzhu University, 1997, 19(2): 21-30.

[4] 陈新, 廖志红, 李德建. 节理倾角及连通率对岩体强度、变形影响的单轴压缩试验研究[J]. 岩石力学与工程学报, 2011, 30(4): 782-789.

CHEN Xin, LIAO Zhihong, LI Dejian. Experimental study of effects of joint inclination angle and connectivity rate on strength and deformation properties of rock masses under uniaxial compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(4): 782-789.

[5] 夏才初, 肖维民, 刘远明. 非贯通节理的岩桥弱化力学模型研究[J]. 岩石力学与工程学报, 2010, 29(8): 1538-1545.

XIA Caichu, XIAO Weimin, LIU Yuanming. Study of mechanical model for weakening process of discontinuous joint rock bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(8): 1538-1545.

[6] 刘远明. 基于直剪试验的非贯通节理岩体扩展贯通研究[D]. 上海: 同济大学土木工程学院, 2007: 75-103.

LIU Yuanming. Study on failure models and strength of rockmass containing discontinuous joints in direct shear[D]. Shanghai: Tongji University. School of Civil Engineering, 2007: 75-103.

[7] 吴顺川, 周喻, 高利立, 等. 等效岩体技术在岩体工程中的应用[J]. 岩石力学与工程学报, 2010, 29(7): 1435-1441.

WU Shunchuan, ZHOU Yu, GAO Lili, et al. Application of equivalent rock mass technique to rock mass engineering[J]. Chinese Journal of Rock Mechanics and Engineering, 2010, 29(7): 1435-1441.

[8] 周喻, 吴顺川, 张晓平. 岩石节理直剪试验颗粒流宏细观分析[J]. 岩石力学与工程学报, 2012, 31(6): 1245-1256.

ZHOU Yu, WU Shunchuan, ZHANG Xiaoping. Macro- and meso-analyses of rock joint direct shear test using particle flow theory[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(6): 1245-1256.

[9] 金爱兵, 李兵, 邓富根. 断续节理对岩体力学性能的影响[J]. 北京科技大学学报, 2012, 34(12), 1359-1363.

JIN Aibing, LI Bing, DENG Fugen. Effect of intermittent joints on the mechanical properties of rock mass[J]. Journal of University of Science and Technology Beijing, 2012, 34(12): 1359-1363.

[10] 刘顺桂, 刘海宁, 王思敬, 等. 断续节理直剪试验与PFC^2D数值模拟分析[J]. 岩石力学与工程学报, 2008, 27(9): 1828-1836.

LIU Shungui, LIU Haining, WANG Sijing, et al. Direct shear tests and PFC^2D numerical simulation of intermittent joints[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(9): 1828-1836.

[11] 范景伟, 何江达. 含定向闭合断续节理岩体的强度特性[J]. 岩石力学与工程学报, 1992, 11(2): 190-199.

FAN Jingwei, HE Dajiang. The strength behavior of rock masses containing oriented and closed intermittent joints[J]. Chinese Journal of Rock Mechanics and Engineering, 1992, 11(2): 190-199.

[12] WANG C, TANNANT D D, LILLY P A. Numerical analysis of the stability of heavily jointed rock slopes using PFC2D[J]. International Journal of Rock Mechanics and Mining Sciences, 2009, 40(3): 415-424.

[13] 李同录, 罗世毅. 节理岩体力学参数的选取与应用[J]. 岩石力学与工程学报, 2004, 23(13): 2182-2186.

LI Tonglu, LUO Shiyi. Determination and application of mechanical parameters for jointed rock masses[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2182-2186.

[14] 周小平, 张永兴, 王建华, 等. 断续节理岩体劈裂破坏的贯通机理研究[J]. 岩石力学与工程学报, 2005, 24(1): 8-12.

ZHOU Xiaoping, ZHANG Yongxing, WANG Jianhua, et al. Study on coalescence mechanism of splitting failure of rock masses with intermittent joints under compression[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(1): 8-12.

[15] ZHANG H Q, ZHAO Z Y, TANG C A, et al. Numerical study of shear behavior of intermittent rock joints with different geometrical parameters[J]. International Journal of Rock Mechanics & Mining Sciences, 2006, 43(5): 802-816.

[16] 赵文. 岩石力学. 长沙: 中南大学出版社, 2004: 65-66.

ZHAO Wen. Rock mechanics[M]. Changsha: Central South University Press, 2004: 65-66.

(编辑  赵俊)

收稿日期：2015-08-15；修回日期：2015-11-12

基金项目(Foundation item)：国家自然科学基金资助项目(51074014)；中央高校基本科研业务费专项资金资助项目(FRF–SD–12–002A) (Project(51074014) supported by the National Natural Science Foundation of China; Project(FRF–SD–12–002A) supported by the Fundamental Research Funds for the Central Universities)

通信作者：金爱兵，副教授，从事岩土工程灾害治理研究；E-mail: jinaibing@ustb.edu.cn