Thin-walled aluminum alloy tube NC precision bending

based on finite element simulation

GU Rui-jie(谷瑞杰), YANG He(杨 合) , ZHAN Mei(詹 梅), LI Heng(李 恒)

School of Materials Science and Engineering, Northwest Polytechnical University,

Xi’an 710072, China

Received 28 July 2006; accepted 15 September 2006

Abstract: Elongation and springback are the bottleneck problems of thin-walled aluminum alloy tube NC precision bending. So thin-walled aluminum alloy tube NC precision bending based on finite element simulation is put forward. The finite element model of thin-walled aluminum alloy tube NC bending is established based on the DYNAFORM platform. The process of thin-walled aluminum alloy tube NC precision bending is simulated with the model and the elongation and springback of tube bending can be gained. A new method of measuring the elongation of thin-walled tube NC precision bending named ‘pressure die measuring method’ is put forward and the computing equations of bending angle, bending radius, blanking length and initial bending section based on elongation and springback angle are derived. The bending angle, bending radius, blanking length and initial bending section of tube bending can be gained with these equations based on the elongation and springback angle from the simulation. The study can be used to control the quality of thin-walled aluminum alloy tube NC bending so that precision bending without redundance can be realized.

Key words: thin-walled tube; NC bending; precision forming; elongation; springback; simulation

1 Introduction

Thin-walled aluminum alloy tube bending parts have been increasingly used in many industry fields such as aviation, aerospace and automobile for their easy satisfaction in light mass and low consuming. The numerical controlled (NC) rotary-draw tube bending technology (Fig.1) not only enables the forming process high technicalization, but also can satisfy the requirements of high precision, high efficiency, digitalization and intellectualization. So the cold NC tube bending process has been developed as one of the most important thin-walled aluminum alloy tube bending technologies [1-3].

Some physics phenomena such as elongation and springback must occur in the process of thin-walled aluminum alloy tube NC bending, which will affect the precision of tube bending. The traditional process flow of tube bending is ‘blanking—tube bending—adjusting—cutting redundance’, of which the material is wasted greatly and the production efficiency is very poor. The precision forming without redundance of thin-walled aluminum alloy tube NC bending is significant to realize the automation of processing, to improve the production efficiency and to deduce the cost.

STELSON et al[4-8] has done a great deal of researches on the precision forming of tube NC bending. In document [4], by measuring the bending moment, the action center of pressure die and the friction force between mandrel and tube, the springback was predicted on line. In Refs. [5] and [6], the method of bend-rebend was used to make the first bend to eliminate trial tubes and the method of process control was developed to optimize the overall control strategy such that the overall tube error is minimized. In Ref. [7]. WANG and STELSON calculated the springback of tube bending with the springback theory of beam bending and the assumption 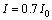 was used as the rotary inertia of bent-tube. In Ref. [8], the analysis model was improved, in which an approximate expression in trigonometric form was introduced for the displacement field and the total deformation theory was employed as a constitutive relation. The solution accurate reached 25%. STELSON has majored in the springback research of tube bending with experiment and analysis. He hasn’t studied the elongation of tube bending. His experiment researches are not comprehensive enough and his analysis researches are not accurate enough because of so many assumptions. In Refs. [9] and [10], a KBS-aided design system of tube bending processes and an automatic tooling design system have been developed respectively. But these systems are almost based on experience expresses and the reliability of design is poor. Up till now, research on tube NC precision bending based on springback and elongation is not found in any document.

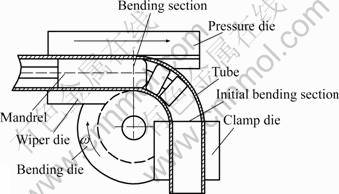
Fig.1 Sketch of tube NC bending

The finite element method can simulate the actual forming process, so that the forming process can be optimized with many virtual experiments and the precision forming process can be realized. So thin-walled aluminum alloy tube NC precision bending based on finite element simulation is put forward in the paper. The finite element model of thin-walled aluminum alloy tube NC bending is established based on the DYNAFORM platform. The process of thin-walled aluminum alloy tube NC precision bending is simulated with the model and the elongation and springback of tube bending can be gained. A new method of measuring the elongation of thin-walled tube NC precision bending named “pressure die measuring method” is put forward and the computing equations of bending angle, bending radius, blanking length and initial bending section are derived. The bending angle, bending radius, blanking length and initial bending section of tube bending can be gained with these equations based on the elongation and springback angle gained from the simulation.

  2 Elastic-plastic finite element model of thin-walled aluminum alloy tube NC bending^[11]

The elastic-plastic finite element model of thin-walled aluminum alloy tube NC bending is established based on the DYNAFORM platform (Fig.2). The whole process of thin-walled tube NC bending can be divided into two stages when it is simulated: The processes of tube bending and mandrel drawing are dealt with as the first stage, which is solved with the dynamic explicit algorithm. The process of tube springback is dealt with as the second stage, which is solved with the static implicit algorithm.

Fig.2 Elastic-plastic finite element model of thin-walled aluminum alloy tube NC bending

The characteristics of the model are as follows:

1) The elastic-plastic finite element model is used, so not only the forming process but also the springback process can be simulated.

2) The combination of dynamic explicit algorithm and static implicit algorithm is used to solve the whole process of thin-walled tube NC precision bending, with which the precision and efficiency of computing are high.

3) Because of the symmetry, half of the model is built and it is constrained with symmetry by *BOUNDARY_SPC_NODE.

4) The dies are expressed as contacting surface and rigid surface.

5) The structure of mandrel are simplified reasonably, mandrel body and mandrel heads are linked to each other through nodes with *CONSTRAINED_ JOINT_SPHERICAL.

6) The mesh of forming area is refined so that it can reflect the forming status well.

7) Fully-integrated-shell-element is used so that the simulation precision can be satisfied.

8) The processes of tube bending and mandrel drawing are dealt with as a stage, in which the bending operation and the mandrel drawing operation are realized by controlling the loading of dies.

9) The whole springback process can be divided into several steps, so the springback of every step is small and springback computing of every step can be controlled, which is useful to accelerate the convergence of spingback computing.

10) Matrix can be controlled to update at every iteration so that the convergence of spingback computing can be reached quickly.

3 Tube elongation of thin-walled aluminum alloy tube NC bending

3.1 Measurement of tube elongation of thin-walled aluminum alloy tube NC bending

The elongation of tube bending is gained from the tube length after bending subtracted by the origin tube length. But because of the tube distortion, it is difficult to measure the length of bent tube accurately. So a new method of measuring the elongation of thin-walled tube NC bending named “pressure die measuring method” is put forward. The method can be used to measure the elongation of thin-walled tube NC bending conveniently and accurately in experiment and simulation. The method is based on the following equation:

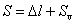                                (1)

where 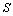  is the relative displacement of pressure die and tube,  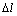the actually elongation of tube bending and  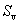the relative displacement of pressure die and tube caused by the disagreement of their velocity.

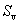 can be gained with the following equation:

                             (2)

where 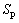  is the displacement of pressure die, which can be gained from the assistant velocity—time curve.

So 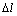 can be gained with the following equation:

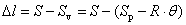               (3)

The steps of measuring the elongation of tube bending are as follows:

1) Before bending, the tube is marked with a line at the location of the back end of pressure die (Fig.3).

2) After bending, the relative displacement of pressure die and tube 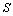 is measured (Fig.4).

3) The actual elongation of tube bending 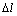 is computed with the above equations.

Fig.3 Location of back end of pressure die before bending

Fig.4 Measurement of relative displacement of pressure die and tube

3.2 Tube elongation of thin-walled aluminum alloy tube NC bending

Based on the simulation of thin-walled aluminum alloy tube NC bending, the tube elongation-bending angle curve is gained with the above elongation measuring method (Fig.5). It can be found from the figure that the tube elongation increases with the process of tube bending and the elongation changes linearly with the bending angle. When a new elongation date of certain bending angle is needed, it can be gained from the curve. Of course, it can be also gained by simulation.

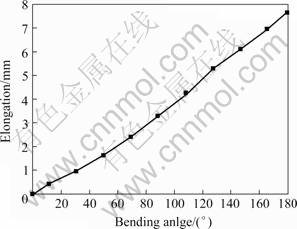
Fig.5 Elongation—bending angle curve of thin-walled aluminum alloy tube NC bending

4 Springback and its compensation of thin-walled aluminum alloy tube NC bending

4.1 Springback angle and its compensation

The springback of thin-walled aluminum alloy tube NC bending will cause the bending angle decreasing. Based on the simulation of thin-walled aluminum alloy tube NC bending, the springback angle-bending angle curve is gained (Fig.6). It can be found from the figure that the springback angle increases almost linearly with the bending angle. The curve is fitted with the linear equation 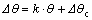  and the fitting error is very small, which means the linear correlation is fine. The springback of the curved region  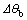is proportional to the bend angle  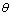(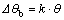). The constant part of the springback 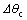is the springback of the transition region near the two ends of the curved region where the tube is not plastically deformed[5-6].

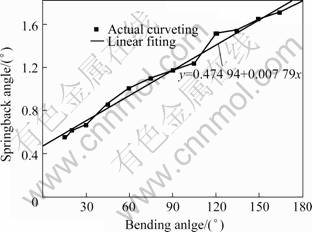
Fig.6 Springback angle—bending angle curves of thin-walled aluminum alloy tube NC bending

The springback angle should be compensated with over-bending for thin-walled aluminum alloy tube NC precision bending. The principle is to over-bending tube certain degree so that the actual forming angle after springback can satisfy the requirement. The relationship between forming angle (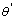) and bending angle (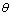) is as the following equation:

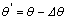                                 (4)

The springback angle 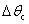 can be gained with the equation:

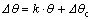                             (5)

So，the bending angle 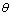 can be gained with the equation:

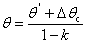                              (6)

4.2 Springback radius and its compensation

The springback of thin-walled aluminum alloy tube NC bending will cause the bending radius to increase. Because the transition region will straighten during springback, so the length of the curved region will be shortened with. So, the length of the curved region before springback and that of the curved region after springback satisfy the equation:

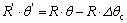.                        (7)

So the springback radius 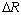 can be gained with the equation:

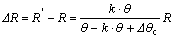                 (8)

The springback radius 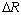 should be compensated with decreasing the bending radius  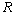for thin-walled aluminum alloy tube NC precision bending, so that the actual forming radius  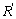after springback can satisfy the requirement. The bending radius  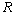can be gained with the equation:

                          (9)

5 Determination of blanking length and initial bending section of thin-walled aluminum alloy tube NC bending

5.1 Blanking length of thin-walled aluminum alloy tube NC bending

Because the transition region will straighten during springback, so the length of the straight region will be increased. The straight region increasing length of each tube end 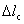 can be gained with the equation:

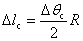                              (10)

The increasing of bending radius during springback will cause the transition section between curved region and straight region offset with  (Fig.7).

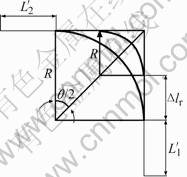
Fig.7 Transition section offset caused by increasing of bending radius

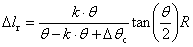                 (11)

The transition section offset caused by springback  can be gained with the equation:

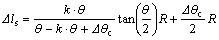         (12)

So, the blanking length of thin-walled aluminum alloy tube NC precision bending is:

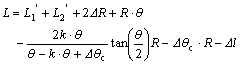      (13)

where 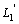  and  are the front and back straight region length of bent tube respectively.

5.2 Initial bending section of thin-walled aluminum

alloy tube NC bending

Because the transition section offset caused by springback is , so the initial bending section of thin-walled aluminum alloy tube NC bending should be put backward with . The location of initial bending section can be determined with the distance between the initial bending section and the front end of tube L₁:

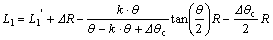 (14)

6 Conclusions

Thin-walled aluminum alloy tube NC precision bending based on finite element simulation is put forward in the paper. The elastic-plastic finite element model of thin-walled aluminum alloy tube NC bending is established based on the DYNAFORM platform. The process of thin-walled aluminum alloy tube NC bending is simulated with the model and the elongation and springback of tube bending can be gained. A new method of measuring the elongation of thin-walled tube NC precision bending named “pressure die measuring method” is put forward and the computing equations of bending angle, bending radius, blanking length and initial bending section are derived. The bending angle, bending radius, blanking length and initial bending section of tube bending can be gained with these equations based on the elongation and springback angle gained from the simulation. The study can be used to control the quality of thin-walled aluminum alloy tube NC bending so that thin-walled aluminum alloy tube NC precision bending without redundance can be realized, which is very important to improve the efficiency and reduce the cost of thin-walled aluminum alloy tube NC bending.

References

[1] YANG He, LIN Yan, SUN Zhi-chao. Review of advanced plastic processing technology and tube forming facing 21st century[A]. Symposium of 2nd China Science Association Annual Conference[C]. Beijing: Press of Science and Technology, 2000: 745-746. (in Chinese)

[2] YANG H, ZHAN M, LIU Y L. Some advanced plastic processing technologies and their numerical simulation[J]. Journal of Materials Processing Technology, 2004, 151: 63-69

[3] ZHAN M, YANG H, JIANG Z Q. A study on a 3D FE simulation method of the NC bending process of thin-walled tube[J]. Journal of Materials Processing Technology, 2002, 129: 273-276.

[4] LI H Z, FAGERSON R, STELSON K A. A Method of adaptive control of rotary-draw thin-walled tube bending with springback compensation[J]. Transactions Of NAMRI/SME, 1994, XXII: 25-28.

[5] LOU Hua-zhou, Stelson K A. Three-dimensional tube geometry control for rotary draw tube bending, part 1: bend angle and overall tube geometry control[J]. Journal of Manufacturing Science and Engineering, 2001, 123: 258-265.

[6] LOU Hua-zhou, Stelson K A. Three-dimensional tube geometry control for rotary draw tube bending, part 2: statistical tube tolerance analysis and adaptive bend correction[J]. Journal of Manufacturing Science and Engineering, 2001, 123: 266-271.

[7] WANG W C, STELSON K A. Computer aided manufacturing for three-dimensional tube bending with on-line springback compensation. Journal of engineering for industry[J]. Transactions of North American Manufacturing Institute, 1991: 70-76.

[8] PAN K, STELSON K A. On the plastic deformation of a tube during bending. Journal of engineering for industry[J]. Transactions of Namri/Sme, 1995, 117(11): 494-500.

[9] JIN Z, LUO S, DANIEL FANG X. KBS-aided design of tube bending process[J]. Engineering Applications of Artificial Intelligence, 2001, 14: 599-606.

[10] Strano M. Automatic tooling design for rotary draw bending of tubes[J]. International Journal of Advanced Manufacture Technology, 2005, 26: 733-740.

[11] GU Rui-jie, YANG He, ZHAN Mei. Springback of thin-walled tube NC precision bending and its numerical simulation[J]. Trans Nonferrous Met Soc China, 2006, 16(Special 1,Part B): 631-638.

(CHEN Ai-hua)

Foundation item: Project (50225518) supported by the National Science Foundation of China for Distinguished Young Scholars; Project (50175092; 59975076) supported by the National Natural Science Foundation of China; Project supported by the Teaching and Research Award Program for Outstanding Young Teachers in Higher Education Institutions of MOE, PRC; Project (04H53057) supported by the Aeronautical Science Foundation of China; Project (Z200518) supported by the Graduate Starting Seed Fund of Northwestern Polytechnical University; Project (20020699002) supported by the Specialized Research Fund for the Doctoral Program of Higher Education

Corresponding author: YANG He; Tel: +86-29-88495632; Fax: +86-29-88495632; E-mail: yanghe@nwpu.edu.cn