DOI： 10.11817/j.issn.1672-7207.2020.10.024
一种弯剪型软钢阻尼器的力学性能
王威，王万志，梁宇建，向照兴，韩斌
(西安建筑科技大学 土木工程学院，陕西 西安，710055)
摘要：为解决现有部分金属阻尼器平面外刚度低，易局部屈曲等问题，提出一种波形软钢阻尼器，考虑波形板放置形式，设计2个试件，并进行拟静力试验研究。基于试验试件的结构形式和尺寸，建立对应的2个有限元模型，分别采用双线性随动强化模型、非线性随动强化模型和混合强化模型进行有限元计算。在此基础上，对试件和模型宏观上的受力变形以及微观上的应变发展规律进行对比分析，进而对水平波形软钢阻尼器拓展因素进行分析。研究结果表明：这种波形软钢阻尼器具有稳定的滞回性能，水平波形软钢阻尼器的耗能性能优于竖向波形软钢阻尼器的耗能性能，但其承载力要比竖向波形软钢阻尼器的低。在混合强化模型下，波形软钢阻尼器模型的力学参数与试验结果吻合度较高，说明混合强化模型是波形软钢阻尼器比较精确的本构模型；当腹板高宽比为0.9时，阻尼器的耗能能力和承载能力最佳。
关键词：波形；软钢阻尼器；滞回性能；本构模型；高宽比
中图分类号：TU352.1；TU317.1 文献标志码：A
文章编号：1672-7207（2020）10-2925-16
Mechanical performance of a flexural shear mild steel damper
WANG Wei, WANG Wanzhi, LIANG Yujian, XIANG Zhaoxing, HAN Bin
(School of Civil Engineering, Xi′an University of Architecture and Technology, Xi′an 710055, China)
Abstract: In order to solve the problem that the existing metal damper has low out-of-plane stiffness and is vulnerable to local buckling, a corrugated mild steel damper was proposed. Taking the layout of corrugated plates as the variable parameter, two specimens were designed and two quasi-static tests were carried out. Two corresponding finite element models were established based on the structural form and size of the test specimen, and were analyzed by using bilinear follow-up strengthening model, nonlinear follow-up strengthening model and hybrid strengthening model. Then, the deformation and microscopic strain of the specimen and model were compared and analyzed, and the expansion factor analysis of the horizontal corrugated mild steel damper was carried out. The results show that the corrugated mild steel damper has stable hysteresis performance, and the energy-dissipation performance of the horizontal mild steel damper is superior to that of the vertical corrugated soft steel damper, while the bearing capacity is lower. The finite element analysis results manifest that when using hybrid strengthening model, the mechanical property of the corrugated mild steel damper model agrees well with the experimental results, indicating that the hybrid strengthening model is a more accurate constitutive model of the corrugated mild steel damper. The damper has the lowest energy dissipation and the best carrying capacity when the depth-width ratio of the web is 0.9.
Key words: corrugated; mild steel damper; hysteretic behavior; constitutive model; depth-width ratio
钢材是应用最广泛的建筑材料之一，不发生断裂之前，钢材能够表现出良好的耗能能力，因此，金属阻尼器广泛采用钢材作为原材料。近几十年来，国内外学者研究了各式各样的阻尼器，如U形钢板阻尼器[1-2]、带缝钢板阻尼器[3]、轴向拉压型阻尼器[4]、环形钢板阻尼器[5]、X形阻尼器[6-7]和三角形阻尼器[8-9]等。MAJIDJ等[10]提出了一种活塞式的金属阻尼器(PMD)，该阻尼器由一组内轴互联的空心钢板组成，研究发现PMD的滞回性能良好，并且满足规范规定的低周疲劳性能。通过有限元模拟，确定了这种阻尼器的等效刚度和屈服荷载的关系式。徐艳红等[11]根据外形特征通过理论计算，提出一种抛物线外形阻尼器，通过对4个试件进行试验研究和数值模拟，发现理论计算结果、试验研究结果和数值模拟结果较吻合，可通过几何尺寸的变化来设计出合理的阻尼器。低屈服点钢(low-yield-point steel，LYP)由于其屈服强度低，能较早进入屈服，可利用屈服后的塑性变形来消耗地震能量[12]，故常用来作为阻尼器的核心耗能构件。孙威等[13]提出一种软钢阻尼器，该阻尼器由钢棒耗能元件以阵列方式排列构成，其截面分为等截面和变截面，且截面面积是该耗能元件耗能能力的主要控制参数，通过对不同截面形状的阻尼器进行数值模拟分析，发现等截面耗能棒体的耗能能力取决于棒体的直径；变截面耗能棒体的耗能能力优于等截面棒体的耗能能力。许立言等[14]针对滞回特性、低周疲劳性能以及耗能减震能力，进行了3组采用低屈服点钢BLY160的剪切型阻尼器的拟静力试验，发现低屈服点钢材随等效塑性应变的累积有明显的循环强化现象，采用低屈服点钢的剪切型阻尼器初始刚度大，屈服位移小，变形能力强，具有良好的滞回性能和稳定的耗能特性。由于平钢板阻尼器面外刚度较小，为了增大其面外刚度，通常在腹板上增设加劲肋，这一工艺增大了阻尼器的初始变形，因此，应研发一种有大变形能力的阻尼器。本文作者通过设计一种波形软钢阻尼器，采用波形腹板来增大阻尼器的面外刚度，然后通过基本性能试验以及基于不同强化模型下的数值模拟计算，研究波形软钢阻尼器的抗震性能。
1 试验概述
1.1 试件设计
本文共设计2个波形软钢阻尼器，即水平波形软钢阻尼器(CMSD-1)和竖向波形软钢阻尼器(CMSD-2)，试件使用低屈服点钢，等级为Q160。2个试件均由中间4块波形板与上下端板焊接而成，试件加工中使翼缘和两边腹板各留1 cm的空隙以便于加载过程中充分发挥各自的变形能力，翼缘和腹板均反对称布置。试件的材料性能见表1，试件参数见表2。2个试件的具体构造如图1所示，具体尺寸见图2。
表1 试件的材料性能
Table1 Mechanical properties of specimens
表2 试件参数
Table2 Parameters of specimens
图1 试件构造示意图
Fig. 1 Construction diagrams of specimens
图2 试件尺寸示意图
Fig. 2 Size diagrams of specimens
1.2 试验加载装置
试验加载装置如图3所示。本文规定试件远离作动器的一端为东侧。为防止试件在加载过程中发生滑动，将试件的底梁用压梁和地面台座进行固定。根据以往经验，软钢阻尼器在加载过程中会有大变形，从而导致应变片脱落。本次试验中，为使数据采集顺利进行，应变片采取满贴的方式，位移计布置如图4所示。
图3 试件加载装置
Fig. 3 Test loading device
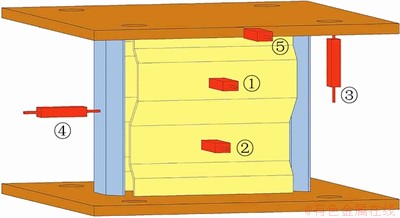
图4 位移计布置示意
Fig. 4 Displacement gauges arrangement
1.3 试验现象及分析
本次试验采用荷载-位移混合控制的加载制度[15]，定义推力为正，拉力为负。在加载初始的荷载控制阶段，第一级加载为10 kN，后续每一级的加载制度比前一级多10 kN。前5级加载，试件无任何变形，处于弹性阶段，直至加载到60 kN时，南侧腹板向外扩大，北侧腹板向内收缩；当加载到-60 kN时，南北腹板又回至原位；当加载到90 kN时，荷载-位移曲线出现明显拐点，此时认为试件开始屈服，屈服位移为2 mm，改用位移控制加载，将屈服位移定义为△y，后面每一级的加载制度比前一级大0.5△y，每一级循环3圈。当拉至-9 mm第1圈时，北侧腹板右下端的波角近乎被拉平；推至10 mm第1圈时，南北的腹板均发生小幅度的顺时针扭转；当拉至-11 mm第1圈时，试件发出清脆的响声，东侧翼缘左下角出现1条长约0.5 cm的裂缝；在推至15 mm第1圈时，南腹板的裂缝延伸至5 cm，并且内外贯通，同时北腹板左下端出现1条新的长约1 cm的裂缝；当推拉至15 mm的第3圈时，翼缘和腹板接触明显，发出较大的摩擦声；在推至16 mm第1圈时，南腹板左下角的裂缝宽度变大，且底部的波角变大；当拉至-16 mm第1圈时，在南侧腹板中下段也出现数条细微裂纹；当推至17 mm的第1圈时，承载力下降到峰值点的85%左右，此时停止加载，试件CMSD-1破坏形态和残余变形分别如图5和图6所示。
图5 试件CMSD-1破坏形态
Fig. 5 Failure model of CMSD-1
图6 试件CMSD-1残余变形
Fig. 6 Residual deformation of CMSD-1
试件CMSD-2采用同样的加载制度，在整个荷载控制阶段，出现少量焊渣掉落的现象，但试件未发生任何变形。直至加载到120 kN时，荷载-位移曲线出现拐点，认为此时试件CMSD-2进入塑性阶段，屈服位移△y等于1 mm；当拉至-1.5 mm第1圈时，南侧腹板的右下端波角被拉大，试件整体变形不明显；当推至3.5 mm的第2圈时，南腹板左下端2~6 mm处出现裂纹，并且在北侧腹板的右下端出现1条长约1.5 cm的裂缝；当拉至-4 mm第1圈时，试件CMSD-2整体向西发生倾斜，并且在北侧腹板的左下角内侧出现1条长约3 cm的裂缝；在推至4.5 mm第1圈时，南侧腹板左下角出现1条长约3 cm的裂缝；当推至5.5 mm第1圈时，北侧腹板在推至3.5 mm第2圈出现的裂缝扩展至9 cm；在推至5.5 mm第2圈时，南侧腹板的裂缝也扩展到8 cm，随着加载的不断进行，试件变形愈加明显，并且裂缝也逐渐扩大，在加载到14 mm时，试件承载力下降严重，停止加载。可以看出，试件CMSD-2在整个加载过程中经历了屈服、塑性变形、初裂和失效这4个阶段。试件破坏形态和最终残余变形分别如图7和图8所示。
图7 试件CMSD-2破坏形态
Fig. 7 Failure model of CMSD-2
图8 试件CMSD-2残余变形
Fig. 8 Residual deformation of CMSD-2
2 试验结果及分析
2.1 滞回曲线、力学特征点和等效黏滞阻尼系数计算分析
试件的滞回曲线如图9所示。可见试件CMSD-1的滞回环较饱满，面积大于试件CMSD-2的滞回环面积，出现这一现象的原因是，试件CMSD-1的腹板为水平波，翼缘主要抗弯，腹板主要抗剪，腹板和翼缘的刚度合理匹配，腹板可以充分发挥作用；而竖波腹板的刚度过大，直至加载结束，腹板只有底部有较大变形。水平和竖向波软钢阻尼器均有拉压不平衡现象，竖向波形软钢阻尼器更为明显，这是因为竖波软钢阻尼器在水平方向上会产生一种明显的拉压应力场，其次是推时产生的剪切变形使试件出现一些细小裂纹，在反向加载时只需施加较小的力便可使裂纹闭合。
图9 试验试件滞回曲线
Fig. 9 Hysteresis curves of specimens
试件延性通过位移延性系数μ来表示，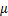
越大，表示延性越好。
(1)
式中：△d为试件的极限位移。本文采用几何作图法确定试件的屈服位移△y[15]。根据图9计算得到试件力学特征点参数如表3所示。
表3 力学特征点的荷载与位移
Table3 Load and displacement of mechanical characteristic points
用黏滞阻尼系数
[15]来评估试件耗能能力，黏滞阻尼系数越大，耗能能力越强。计算示意图如图10所示(其中△为位移，P为荷载)，计算公式为
(2)
式中：
为图10中滞回曲线所包围的面积；
为图10中三角形OAC与OBF的面积之和。
图10 等效黏滞阻尼系数计算
Fig. 10 Calculation of equivalent viscosity damping coefficient
计算出2个试件的等效黏滞阻尼系数并进行对比分析，如图11所示。从图11可见：加载初期试件CMSD-2的较大，但随着加载进行，试件CMSD-1的逐渐超过试件CMSD-2的。这说明水平波形软钢阻尼器的耗能能力强于竖向波形软钢阻尼器的耗能能力。
图11 等效黏性阻尼系数-位移曲线
Fig. 11 Equivalent viscous damping coefficient-displacement curve
2.2 应变分析
在加载过程中，由于试件变形过大，也出现了应变片脱落的现象，故这里选用输出较完好的数据，试件测点的位置与编号分别如图12和图13所示。
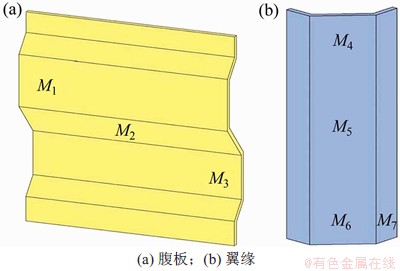
图12 试件CMSD-1所取测点示意图
Fig. 12 Diagrams of measuring points of CMSD-1
图13 试件CMSD-2所取测点示意图
Fig. 13 Diagrams of measuring points of CMSD-2
试件CMSD-1腹板和翼缘板上的σ1/σy(主应变/屈服应变)随位移变化曲线如图14所示。从图14可见：由于加载过程中，腹板变形较大，应变花和应变片松动，数据采集不够完全，所以，取推拉位移在±4 mm以内的主应变，试件CMSD-1腹板3个测点的应变发展大体趋势相同，均随着位移的增大而增大，试件CMSD-1的测点M1和M3在同一级位移下，拉压应变差距较大的原因是低屈服点钢屈服应变小，测点在位移较小的时候便进入塑性变形，从而产生残余应变，而且在推时会产生细微裂纹，此时会发生应变重分布，使得回拉时，用较小的力便能达到加载位移。在位移达到0.5 mm后，测点M1和测点M3的应变上升速度大致相同，远比测点M2的大。为方便定义，后续将纵坐标轴(σ1/σy)简化为y轴。将3个点的应变与直线y=1比较，可以看出：测点M1和M3到达屈服应变时对应的加载位移比测点M2的小，所受应力较大，首先屈服，这与试件CMSD-1在加载过程中从角部开始变形的现象相吻合。
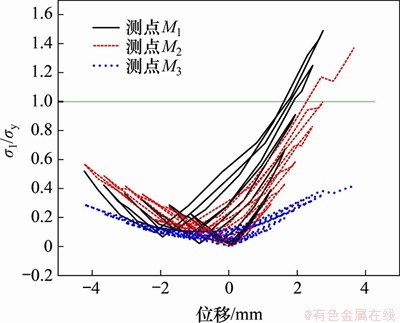
图14 试件CMSD-1腹板测点σ1/σy随位移的变化
Fig. 14 σ1/σy changes of CMSD-1 web measuring points with displacement
试件CMSD-1翼缘的σ1/σy随位移变化曲线如图15所示。相比于腹板的主应变，翼缘板的主应变较大，这也是翼缘设计成波形的原因。本文提出的波形软钢阻尼器在受力形式上是一种弯剪型阻尼器，由于腹板是水平波，其平面外刚度很小，所以，抗弯性能主要由翼缘承担。与腹板主应变相似，翼缘板的主应变也呈现“V”字形，近似关于直线△=0(位移为0 mm)对称；在4个测点中，M7最早达到屈服应变，而且其应变上升的速度远比其他3个测点的大，M6的主应变次之，这也与前文描述的翼缘左下角最先出现屈曲和裂缝这一试验现象相吻合；M4，M6和M7测点均到达了屈服应变，而测点M5在加载后期才达到屈服应变。
图15 试件CMSD-1翼缘测点σ1/σy随位移的变化
Fig. 15 σ1/σy changes of CMSD-1 flange measuring points with displacement
试件CMSD-2腹板所取测点的σ1/σy随位移变化曲线如图16所示。可见，所取3个测点的主应变均到达了屈服应变，均随着位移的增大而增大，3个测点中，测点Ⅲ主应变的数值和上升速度远比测点Ⅰ和测点Ⅱ的大，这也与试验现象即试件CMSD-2腹板最先从2个底部开始屈曲相吻合；而测点Ⅰ和测点Ⅱ在受拉方向上，主应变随位移发展规律近乎一致，而在推向上，测点Ⅰ的主应变和上升速度要比测点Ⅱ的大。相比于试件CMSD-1的所取测点的主应变随位移发展的曲线，试件CMSD-2腹板的主应变随位移发展曲线较为复杂，这是因为竖向波形钢板会产生一种水平方向的拉压效应。将3个点的主应变与直线y=1相比较，可以看出：测点Ⅰ和测点Ⅱ到达屈服应变时对应的加载位移比测点Ⅲ要大，测点Ⅲ在加载幅值较小时便屈服，其次是测点Ⅰ，最后是测点Ⅱ。
图16 试件CMSD-2腹板测点σ1/σy随位移的变化
Fig. 16 σ1/σy changes of CMSD-2 web measuring points with displacement
试件CMSD-2翼缘的主应变随位移变化曲线如图17所示。可见，腹板的主应变要大于翼缘板的主应变，到加载结束时，腹板角部的主应变能达到0.004 14，而翼缘板的最大应变只能达到0.002 68，这是因为波形腹板竖向放置，面外刚度很大，所以在试件CMSD-2中，翼缘板变形特征不大，这也与试验加载过程中，几乎都是腹板出现变形特征，而在加载快结束时，翼缘角部才出现可见的屈曲变形的现象相吻合；翼缘板上的3个测点，上下测点主应变的数值与发展趋势都很接近，而在同级位移加载时，中间测点的主应变只有上下测点的10%，3个测点的形状也接近于“V”字形，近似关于直线△=0对称；将3个测点的主应变与直线y=1比较，可以看出：只有编号Ⅳ和编号Ⅵ的主应变达到了屈服应变，编号Ⅳ的主应变到达屈服应变的速度比编号Ⅵ的略快。
图17 试件CMSD-2翼缘测点σ1/σy随位移的变化
Fig. 17 σ1/σy changes of CMSD-2 flange measuring points with displacement
3 数值模拟分析
3.1 不同强化模型的计算结果
建立与试验试件结构形式完全相同的6个模型，本文选取常见的双线性随动强化模型[16]、非线性随动强化模型[17-18]和混合强化模型[19-21]分别对6个模型进行数值模拟分析，模型具体参数见表4。
表4 模型参数
Table4 Models parameter
将波形板水平放置时的模型计算结果与试验结果进行对比，分别如图18~20所示。
图18 试件CMSD-1与模型CMSD1-BR力学性能对比
Fig. 18 Comparison of mechanical performance between CMSD-1 and CMSD1-BR
图19 试件CMSD-1与模型CMSD1-NR力学性能对比
Fig. 19 Comparison of mechanical performance between CMSD-1 and CMSD1-NR
从图18可以看出：模型CMSD1-BR的滞回曲线显著比试件CMSD-1的饱满，未出现任何捏缩现象；模型CMSD1-BR和试件CMSD-1的骨架曲线在加载初期近乎重合；模型CMSD1-BR的骨架曲线未出现下降段，在整个加载过程中单调递增，到加载中期后，骨架曲线逐渐趋于平稳，但试验试件CMSD-1的骨架曲线在加载到后期出现了下降段，并最终下降到峰值承载力的85%以下，认为达到失效并破坏。
从图19可得：模型CMSD1-NR的滞回曲线比试件CMSD-1的滞回曲线饱满；模型CMSD1-NR和试件CMSD-1的骨架曲线在加载初期也近乎重合；模型CMSD1-NR的恢复力直至加载制度的最后1级才出现略微下降；模型CMSD1-NR骨架曲线在整个加载过程中单调递增，到加载中后期，模型CMSD1-NR的恢复力上升速度下降，骨架曲线也逐渐趋于平稳，但试验试件CMSD-1的骨架曲线在加载到后期出现了下降段，并最终下降到峰值承载力的85%以下，认为达到失效并破坏。
从图20可得：模型CMSD1-CM的滞回曲线比试件CMSD-1的滞回曲线饱满，模型CMSD1-CM和试件CMSD-1的骨架曲线吻合度良好，在加载前期均呈线性递增发展趋势；在受推力时，同一位移下恢复力下降，而在受拉力时，试件CMSD-1先于模型CMSD1-CM一个加载级发生恢复力下降，试件CMSD-1和模型CMSD1-CM均经过了弹性、弹塑性、初裂和失效阶段。
将波形板竖向放置时的模型计算结果与试验结果进行对比，分别如图21~23所示。
从图21可以看出：与试件CMSD-1与模型CMSD1-BR的对比相同，模型CMSD2-BR的滞回曲线也比试件CMSD-2的饱满，模型CMSD2-BR和试件CMSD-2的骨架曲线在加载初期也近乎重合；而且模型CMSD2-BR骨架曲线也未出现下降段，在整个加载过程中单调递增，到加载中后期，恢复力上升速度下降，骨架曲线逐渐趋于平稳，试验试件CMSD-2的骨架曲线在加载到后期出现了下降段，并最终下降到峰值承载力的85%以下，认为达到失效并破坏。
从图22可以看出：模型CMSD2-NR和试件CMSD-2的滞回曲线均出现了捏拢现象，但是前者的滞回曲线较饱满；模型CMSD2-NR和试件CMSD-2的骨架曲线在加载前期均呈线性递增，到加载中后期，恢复力上升速度下降，骨架曲线逐渐趋于平稳；模型CMSD2-NR受拉时，在倒数第3级加载位移时开始出现恢复力下降现象，而试件CMSD-2在倒数第2级才出现恢复力下降。
图20 试件CMSD-1与模型CMSD1-CM力学性能对比
Fig. 20 Comparison of mechanical performance between CMSD-1 and CMSD1-CM
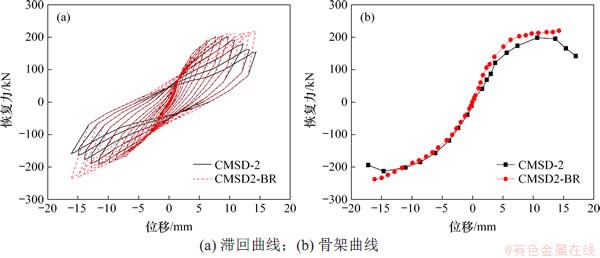
图21 试件CMSD-2与模型CMSD2-BR力学性能对比
Fig. 21 Comparison of mechanical performance between CMSD-2 and CMSD2-BR
根据图23可以看出：模型CMSD2-CM的滞回曲线与试件CMSD-2的滞回曲线吻合度良好，由于在有限元分析中，边界条件和构件间的接触等都是理想状态，所以，模型CMSD2-CM的滞回曲线较试件CMSD-2的滞回曲线饱满；模型CMSD2-CM和试件CMSD-2的骨架曲线在加载前期单调递增，到加载中后期，均出现了恢复力上升速度下降现象，模型CMSD2-CM与试件CMSD-2在同一加载位移处发生了恢复力下降的现象。
将上述3种不同强化模型分析结果的特征点参数与试验结果特征点参数整合，结果如表5所示。从表5可以看出：对于本次试验试件的结构形式，钢板本构选用双线性随动强化模型和非线性随动强化模型时，数值模拟分析结果与试验结果误差较大；当选用混合强化模型时，有限元分析结果和试验结果吻合度较高，说明混合强化模型适用于本次试验试件。
表5 不同强化模型和试验结果的相对误差
Table5 Relative error between different strengthened models and test results
图22 试件CMSD-2与模型CMSD2-NR力学性能对比
Fig. 22 Comparison of mechanical performance between CMSD-2 and CMSD2-NR
图23 试件CMSD-2与模型CMSD2-CM力学性能对比
Fig. 23 Comparison of mechanical performance between CMSD-2 and CMSD2-CM
3.2 受力变形对比分析
在选用混合强化模型的基础上，对处于不同力学状态下的试件和对应模型的受力和变形进行对比分析。现研究模型CMSD1-CM在模拟加载过程中不同状态下的应力、塑性应变，并与试验结果进行对比分析。将模型CMSD1-CM不同状态时的应力云图进行对比，如图24所示。
从图24可以看出：波形腹板首先从4个角部屈服并逐渐向中间发展，直至达到破坏状态，波形腹板4个角部的应力也远大于波形腹板中间部位的应力；在达到破坏状态时，腹板也充分发挥了变形耗能的作用。由于腹板波纹方向是水平向的，故其抗弯刚度几乎可以忽略不计，抗弯全由翼缘承担，所以，翼缘上下角部应力大于其中间部位的应力，并且其角部出现明显的局部屈曲。
图24 试件CMSD-1与模型CMSD1-CM受力和变形对比
Fig. 24 Comparison of stress and deformation between CMSD-1 and CMSD1-CM
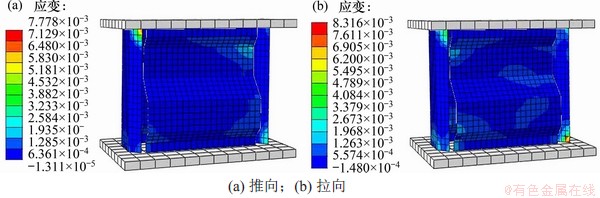
图25 模型CMSD1-CM屈服状态下的应变云图
Fig. 25 Strain cloud diagram under yield state of CMSD1-CM
模型CMSD1-CM在屈服状态下的塑性应变云图如图25所示，在图15的基础上作2条辅助线，如图26所示。图26中，
和
分别表示试件CMSD-1 在推、拉方向上的屈服位移。以M7点为例：根据试验时在试件上划分的网格，找到应变片对应于应力云图位置，在推向屈服状态时模型CMSD1-CM的M7点应变为0.001 08，而试件CMSD-1测点M7此时应变为0.001 22，相对误差只有11.5%。
图26 试件CMSD-1翼缘板推拉屈服状态应变图
Fig. 26 Strain diagram of push-pull yield state of CMSD-1 flange
模型CMSD1-CM推拉破坏状态下的应变云图如图27所示。对比图26和图27可以发现：模型CMSD1-CM推拉向应变也不平衡，拉向应变大于推向应变，而且翼缘板上下测点的应变明显大于中间测点应变，这也与试验结果相吻合；当取推向最后一级即破坏状态的加载位移时，试件CMSD-1测点M7主应变为0.003 38，而模型CMSD1-CM的主应变为0.004 07，约为测点M7的1.20倍；当取拉向最后一级加载位移时，试件CMSD-1测点M7主应变为0.004 56，模型CMSD1-CM的主应变为0.005 28，约为测点M7的1.15倍。现研究模型CMSD2-CM在模拟加载过程中不同状态下的应力、塑性应变及面外变形，并与试验结果进行对比分析。将模型CMSD2-CM不同状态时的应力云图与试验现象对比，如图28所示。
图27 模型CMSD1-CM破坏状态下的应变云图
Fig. 27 Strain cloud diagram under failure state of CMSD1-CM
图28 试件CMSD-2与模型CMSD2-CM受力和变形对比
Fig. 28 Comparison of stress and deformation between CMSD-2 and CMSD2-CM
从图28可以发现：模型CMSD2-CM在2种受力状态和残余变形下的变形特征与试验结果高度吻合；与水平波形软钢阻尼器不同，竖向波形软钢阻尼器应力从波形腹板底部逐渐向上部发展，在达到破坏状态时，腹板基本全部屈服，说明腹板也充分发挥了变形耗能的作用；翼缘板上下端的应力显著大于中间波段的应力。由于竖向波形软钢阻尼器在平面外刚度较大，所以，其变形很小，耗能性能不如波形钢板水平放置时阻尼器的耗能性能。模型CMSD2-CM在屈服状态下的塑性应变云图如图29所示。
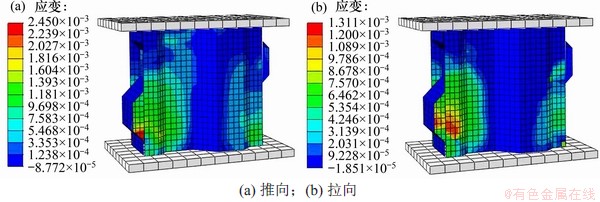
图29 模型CMSD2-CM屈服状态下的应变云图
Fig. 29 Strain cloud diagram under yield state of CMSD2-CM
与试件CMSD-1相同，通过作辅助线，观察屈服状态下测点的应变发展规律，对比图29和图16、图17可以发现：在推向时，测点Ⅰ和测点Ⅲ的应变显著大于测点Ⅱ的应变，与图29(a)的应变分布规律相吻合，而且在推向屈服位移时，3个测点均未达到屈服应变；在拉向时，图16中编号Ⅲ的主应变明显大于其余2个测点的应变，这也与图29(b)中的应变分布情况相吻合。
在推拉向的屈服位移上，翼缘板上3个测点的应变均未达到屈服应变，这与图29中翼缘板上的应变分布情况相同，在屈服位移以内时，3个测点的应变近似相等。模型CMSD2-CM破坏状态下的应变云图如图30所示。对比图30和图16、图17可以发现：模型CMSD2-CM拉向应变大于推向应变，而且翼缘板上下测点的应变明显大于中间测点应变，这与试验结果相吻合；翼缘板中间部位近乎未达到屈服应变。根据试验时对试件的网格划分，换算为网格的位置，输出模型CMSD2-CM对应于试验测点的位移应变，并与试验所得到的应变进行比较，如表6所示。从表6可以发现：试验测点所测得应变与模型CMSD2-CM输出的应变比较吻合，少数测点误差较大，这可能是网格的换算具有误差所致。
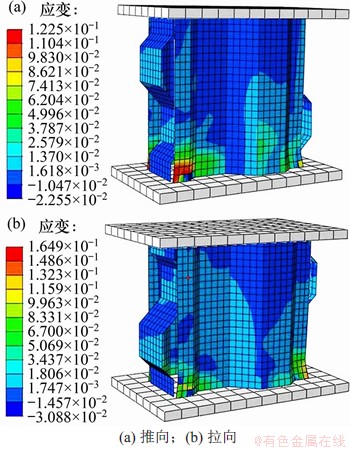
图30 模型CMSD2-CM破坏状态下的应变云图
Fig. 30 Strain cloud diagram under failure state of CMSD2-CM
3.3 拓展因素分析
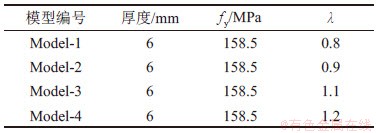
由于数值模拟分析结果与试验结果高度吻合，可见ABAQUS软件的模拟分析结果有一定的参考价值，可以拓展试验工况。本文选用耗能能力较好的水平波形软钢阻尼器作为基本试件，通过数值模拟分析腹板高宽比(λ)对其力学性能的影响。模型参数如表7所示。
将4个模型(Model-1~Model-4)的滞回曲线与模型CMSD1-CM的滞回曲线进行对比，如图31所示。
从图31可以看出：4个模型的滞回曲线与模型CMSD1-CM滞回曲线的形状相似，均呈梭形。计算出4个模型的等效黏滞阻尼系数，如图32所示。
图31 水平波形钢板阻尼器腹板不同高宽比下的滞回曲线对比
Fig. 31 Comparison of hysteretic curves of horizontal corrugated steel plate dampers under different aspect ratio
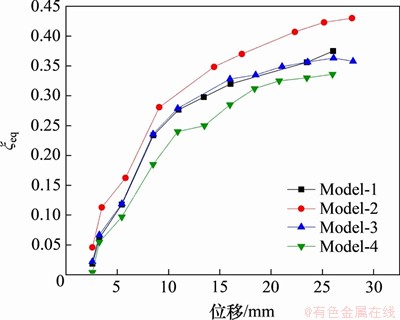
图32 等效黏滞阻尼系数-位移曲线
Fig. 32 Equivalent viscous damping coefficient-displacement curve
从图32可以看出：在整个加载阶段，模型Model-2的等效黏滞阻尼系数均比其余3个模型的大，最大可达到0.44，耗能能力最强；模型Model-4的等效黏滞阻尼系数最小，耗能效果最差；模型Model-1和模型Model-3的等效黏滞阻尼系数随位移变化的曲线几乎重合。4个模型的等效黏滞阻尼系数-位移曲线一直单调递增，在加载后期，均出现增长速率降低的特征。从以上分析得出，当阻尼器腹板高宽比为0.9时，其耗能能力最强，因此，水平波形软钢阻尼器腹板的最佳高宽比为0.9。
表6 试件CMSD-2测点应变与模型CMSD2-CM测点应变的对比
Table 6 Comparison of strain between CMSD-2 and CMSD2-CM measurement points
表7 模型参数
Table7 Parameters of the model
4 结论
1) 本文设计的波形软钢阻尼器具有安装方便，易于更换等优点，而且在力学性能上具有较好的位移延性与耗能能力。水平波形软钢阻尼器的耗能性优于竖向波形软钢阻尼器的耗能性，但其承载力比竖向波形软钢阻尼器的低。水平波形软钢阻尼器的黏滞阻尼系数、延性系数分别是竖向波形软钢阻尼器的1.17倍和1.31倍。
2) 波形软钢阻尼器适用混合强化模型。当选用混合强化模型对波形软钢阻尼器进数值模拟分析时，无论从宏观变形上还是微观的应变发展规律上，均与试验结果吻合度较高。
3) 对于水平波形软钢阻尼器，在保证其结构形式和其他几何特征参数为定量，且腹板高宽比为0.9时，阻尼器的耗能能力最优。
4) 本文提出的波形软钢阻尼器可采用人字支撑的方式放置于梁的跨中位置，主要承担水平方向的荷载。
参考文献：
[1] 杜红凯, 韩淼, 闫维明. 约束U形钢板力学性能的计算方法研究[J]. 土木工程学报, 2014, 47(S2): 158-163.
DU Hongkai, HAN Miao, YAN Weiming. Study on the calculation method of mechanical characteristics for constrained U-shaped steel plates[J]. China Civil Engineering Journal, 2014, 47(S2): 158-163.
[2] KHATIBINIA M, JALAIPOUR M, GHAREHBAGHI S. Shape optimization of U-shaped steel dampers subjected to cyclic loading using an efficient hybrid approach[J]. Engineering Structures, 2019, 197: 108874.
[3] 孔子昂, 王涛, 施唯. 带缝钢板阻尼器受力性能试验研究[J]. 土木工程学报, 2015, 48(9): 11-22.
KONG Zi'ang, WANG Tao, SHI Wei. Experimental study on mechanical properties of steel dampers with slits[J]. China Civil Engineering Journal, 2015, 48(9): 11-22.
[4] 鲁亮, 刘霞, 代桂霞. 轴向拉压型金属阻尼器抗震性能测试及其应用研究[J]. 振动与冲击, 2017, 36(16): 141-147.
LU Liang, LIU Xia, DAI Guixia. An experimental study on the mechanical properties of an axial compression-tension metallic damper and its application[J]. Journal of Vibration and Shock, 2017, 36(16): 141-147.
[5] 姜洪源, 郝德刚, 夏宇宏, 等. 多层环形钢板阻尼器隔振系统建模与仿真研究[J]. 哈尔滨工业大学学报, 2004, 36(3): 290-293.
JIANG Hongyuan, HAO Degang, XIA Yuhong, et al. Research on damper with multilayer steel plates modeling and simulation of isolation system[J]. Journal of Harbin Institute of Technology, 2004, 36(3): 290-293.
[6] 王强, 安立刚, 刘明, 等. 新型钢板阻尼器的减震性能分析[J]. 土木工程学报, 2010, 43(S1): 341-344.
WANG Qiang, AN Ligang, LIU Ming, et al. Analysis on vibration suppression of a new type of planar steel damper[J]. China Civil Engineering Journal, 2010, 43(S1): 341-344.
[7] WHITTAKER A S, BERTERO V V, THOMPSON C L, et al. Seismic testing of steel plate energy dissipation devices[J]. Earthquake Spectra, 1991, 7(4): 563-604.
[8] 李冀龙, 欧进萍. X形和三角形SMA板式阻尼器的阻尼力模型[J]. 地震工程与工程振动, 2002, 22(6): 109-114.
LI Jilong, OU Jinping. Damping force hysteresis loop model for X type and triangle SMA plate dampers[J]. Earthquake Engineering and Engineering Vibration, 2002, 22(6): 109-114.
[9] TSAI K C, CHEN Huanwei, HONG C P, et al. Design of steel triangular plate energy absorbers for seismic-resistant construction[J]. Earthquake Spectra, 1993, 9(3): 505-528.
[10] JARRAH M, KHEZRZADEH H, MOFID M, et al. Experimental and numerical evaluation of piston metallic damper(PMD)[J]. Journal of Constructional Steel Research, 2019, 154: 99-109.
[11] 徐艳红, 李爱群, 黄镇. 抛物线外形软钢阻尼器试验研究[J]. 建筑结构学报, 2011, 32(12): 202-209.
XU Yanhong, LI Aiqun, HUANG Zhen. Experimental study of mild steel dampers with parabolic shape[J]. Journal of Building Structures, 2011, 32(12): 202-209.
[12] 施刚, 高阳, 王珣, 等. 低屈服点钢低周疲劳性能研究[J]. 土木工程学报, 2019, 52(1): 20-26, 52.
SHI Gang, GAO Yang, WANG Xun, et al. Low cycle fatigue properties of low yield point steels[J]. China Civil Engineering Journal, 2019, 52(1): 20-26, 52.
[13] 孙威, 张铁山, 孟宪宏. 软钢棒体阻尼器耗能元件设计与性能分析[J]. 世界地震工程, 2015, 31(2): 196-201.
SUN Wei, ZHANG Tieshan, MENG Xianhong. Design and performance analysis of energy-dissipating element of mild steel rod damper[J]. World Earthquake Engineering, 2015, 31(2): 196-201.
[14] 许立言, 聂鑫, 樊健生, 等. 低屈服点钢剪切型阻尼器试验研究[J]. 清华大学学报(自然科学版), 2016, 56(9): 991-996.
XU Liyan, NIE Xin, FAN Jiansheng, et al. Experimental investigation of low-yield-point steel shear panel dampers[J]. Journal of Tsinghua University(Science and Technology), 2016, 56(9): 991-996.
[15] JGJ/T101—2015，建筑抗震试验规程[S].
JGJ/T101—2015，Specification for seismic test of buildings[S].
[16] 王桂萱, 孙晓艳, 赵杰. 基于不同本构模型的新型软钢阻尼器的滞回性能研究[J]. 防灾减灾工程学报, 2015, 35(3): 296-301.
WANG Guixuan, SUN Xiaoyan, ZHAO Jie. Hysteretic performance study on A new type of mild steel damper based on different constitutive models[J]. Journal of Disaster Prevention and Mitigation Engineering, 2015, 35(3): 296-301.
[17] DAN W J, ZHANG W G, LI S H, et al. An experimental investigation of large-strain tensile behavior of a metal sheet[J]. Materials & Design, 2007, 28(7): 2190-2196.
[18] KAMAYA M, KAWAKUBO M. A procedure for determining the true stress-strain curve over a large range of strains using digital image correlation and finite element analysis[J]. Mechanics of Materials, 2011, 43(5): 243-253.
[19] BARI S, HASSAN T. Anatomy of coupled constitutive models for ratcheting simulation[J]. International Journal of Plasticity, 2000, 16(3/4): 381-409.
[20] CHABOCHE J L. A review of some plasticity and viscoplasticity constitutive theories[J]. International Journal of Plasticity, 2008, 24(10): 1642-1693.
[21] BROGGIATO G B, CAMPANA F, CORTESE L. The Chaboche nonlinear kinematic hardening model: calibration methodology and validation[J]. Meccanica, 2008, 43(2): 115-124.
(编辑 伍锦花)
收稿日期： 2020 -02 -21; 修回日期： 2020 -05 -21
基金项目(Foundation item)：国家自然科学基金资助项目(51578449，51878548)；陕西省自然科学基础研究计划重点项目(2018JZ5013) (Projects(51578449, 51878548) supported by the National Natural Science Foundation of China; Project(2018JZ5013) supported by the Natural Science Basic Research Program of Shaanxi Province)
通信作者：王威，博士，教授，从事高层建筑结构抗震设计研究；E-mail：wangwgh1972@163.com
