Simulation on temperature field of TIG welding of copper without preheating

LEI Yu-cheng(雷玉成), YU Wen-xia(郁雯霞), LI Cai-hui(李彩辉), CHENG Xiao-nong(程晓农)

School of Materials Science and Engineering, Jiangsu University, Zhenjiang 212013, China

Received 26 September 2005; accepted 14 January 2006

Abstract: According to the conservation of energy principle and technology characteristics of tungsten inert gas(TIG), a model of non-steady three-dimensional temperature field for red copper’s TIG welding with a locomotive arc was established. The temperature field of welding pool was calculated with finite element software ANSYS. Indrafted the heat enthalpy conception and the surface distribution dual-ellipsoid model, the demands of welding numerical simulation was primely satisfied. Aimed at bad weldability of red copper, the TIG welding of thick-wall red copper was studied adopting Ar+N₂ without preheating. The results show that the heating effect of arc is evidently enhanced, it is viable to achieve the no preheating TIG welding of red copper. Comparing the experimental values with the calculated ones under different technological parameters, the results indicate that the model and practical course are well matched, which proves that the model is reliable and correct.

Key words: copper; TIG welding; temperature field; simulation

1 Introduction

Fusion welding of red copper easily leads to many defects, such as backing’s lack of fusion, groove’s hard of through-welding, bad surface forming. All these have relations with thermophysical performances of red copper. The heat conductivity of red copper is good, so we should choose welding methods with high heat efficiency and concentrated heat quantity. It is benifical if the heat efficiency is high and the energy is concentrated. TIG welding has prominent virtues of stable arc, concentrated energy capacity, good protection effect and flexible operation. It has already replaced traditional gas welding, carbon arc welding and manual electric-arc welding, and become one of the most widespread melting welding methods for thick-wall red copper.

The welding is a non-equilibrim, transient and quite non-uniform physicochemical metallurgy process, it is difficult to realize real-time, efficient and on-line control. To establish mathematical model of the welding pool using the science method and describe the heat transfer and liquid flow of the welding pool, not only the simulation of complex welding phenomenon can be achieved and the best technological parameter can be confirmed[1-6], but also the foundation for achieving intellectualized control of welding process can be laid. In recent years, many researches about simulation on temperature field of TIG welding the world were developed all over, and many achievements were made [7-10].

In this paper, a model of non-steady three-dimensional temperature field for TIG welding with a locomotive arc was established and the temperature field was calculated with ANSYS. Aimed at the weldability of red copper and in order to improve the welding quantity, the TIG welding of thick-wall red copper was studied adopting Ar+N₂ under non-warming- up condition.

2 Model description

2.1 Construction of control formula

Fig.1 shows the schematic diagram of TIG welding process with a locomotive arc (unfilled with welding wire). As shown in Fig.1, the arc moves along the X-axis at a certain speed u₀. The heat of the electric arc melts the base metal to form welding pool. According to the distributing of the temperature field, the welding pool is divided into two parts of the foreside and the rearward. In the foreside, the input heat wins the outer spread heat. In the rearward, the out spread heat wins the input heat, so it gets solidified.

Fig.1 Schematic diagram of TIG welding system

3-Dimensional model of the welding pool had been built under instable condition. To simplify the calculation, the liquid metal in the welding pool is unable to be pressed sticky fluid and its hydro-mechanical moving is a laminar flow[11]. The supposition that the surface of the welding pool is not deformed, has been proved by both theoretic calculation and experiment[12,13].

In the certain coordinate, the energy formula of the un-pressed fluid is

  (1)

where  ρ is the density; c_p is the specific heat of certain pressure; T is the temperature; k is the coefficient of heat transfer; u, v, w are the fluid’s corresponding velocities in x, y, z dimension of the liquid metals in the welding pool, respectively.

Both of the liquid welding pool and the solid around it are included in the data realm of Eqn.(1). So in the whole data realm, it is a problem between convection and conduction. But for the velocity of the fluid in the solid is zero, actually it is a pure heat transfer calculation in the solid realm[14]. So the result of such calculation will provide the temperature distribution in the solid and the liquid for us. They will be automatically tallied in the interface between the solid and the liquid.

The work piece is in the solid state prior to the welding. After igniting arc, the work piece absorbs the heat of the electric arc. The heat that absorbs with the work piece increases gradually, the temperature also rises gradually, the welding pool appears in the molten bath. With the extension of the welding time, the welding pool is expanding continuously. When the welding pool reaches a certain size, the total amount of heat that the welding pool absorbs just means the heat transmits into the batch and the heat spread out through the work piece surface. It will be in the stable state at this moment. And the welding pool at this moment has an invariable form, and can be regarded as the invariable temperature field which moves with the heat source centre along x-axle at the same speed as the electric arc.

As to the flowing movement that the fluid in the welding pool should satisfy the momentum equation, and its momentum equations are

Along x direction:

    (2)

Along y direction:

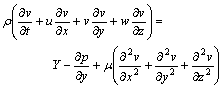    (3)

Along z direction:

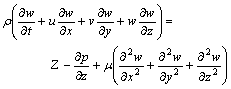    (4)

where  μ is the viscidity coefficient.

In addition, according to the law of conservation of quality in classical mechanics, the systematic quality is unchangeable. The fluid field should also satisfy an additional demand, namely the continuity equation:

                           (5)

The equations mentioned above just describe the control equations of the fluid field and the heat field of welding pool in the transient state, which are influenced by the locomotive electric arc.

2.2 Border condition

The solution area of control equations includes the welding pool and the metal around it. In the whole value range, the solid state area takes mainly solid condition heat-conduction, and the welding pool area takes mainly convection with the liquid metal at a high temperature. The welding process in this study is in the unstable state. So there will be the heat of the electric arc in the surface of the welding pool, and the losing heat of the welding border convection and radiation. Because the heat- conduction rate of copper is high, a large amount of heat will be conducted out from the heating area rapidly during welding. And because of the symmetry of the welding pool, which is in the welding speed direction, we should calculate one half of temperature field of the work piece. The border condition on the surface of the work piece is

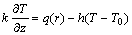                                    (6)

where  q(r) is the density of the thermal current of the electric arc, h is the equivalent coefficient of the radiation and convection heat, respectively.

2.3 Latent heat of phase transition

During TIG welding, melting and solidifying and other phase transitions of the weld metal occur in the welding pool at the same time. It will absorb or give off the latent heat while in phase transition, namely latent heat of phase transition. There is the discontinuity with temperature gradient in the phase transition interface, absorbs the latent heat while melting, and releases the latent heat while solidifying. One method of dealing with phase transition is to adopt the enthalpy method, just define the material’s enthalpy which alternates with the temperature to consider the latent heat. Its relational expression can be shown as

                                     (7)

where  ρ is the density of material, kg/m³; c is the specific heat, J/(kg·K), respectively.

2.4 Mode of heat resource

The Gauss distribution function was adopted to solve the thermal current problem of TIG welding. The longitudinal vertical thermal current was neglected when calculating the heat resource distribution by the two-dimensional heat conduction equation. So only by calculating in three-dimensions, can we actually realize the heat course of welding. The dual-ellipsoid thermal current distribution model was adopted, which was named by GOLDAK et al[15]. We can simplify the dual-ellipsoid model to the surface distribution dual ellipsoid model, for the depth of the TIG welding pool is relatively shallow. To this model, the energy density of the foreside half of the welding pool can be expressed as

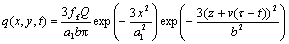(8)

where  f_f is the distribution index of the energy density of the foreside half of the welding pool by the total input thermal power; τ is the lagging factor of the electric arc at the initial moment; Q is the inputting rate of heat; x with ξ-axle at the moment, is just the distance in axle direction from the heat resource centre, and the same as z with ξ-axle, respectively.

The energy density of the rearward half of the welding pool may be pressed as

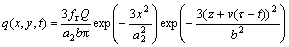(9)

where  f_r is the distribution index of the rearward half of the welding pool by the total input thermal power.

The a₁ and b of the foreside of the welding pool that are independent of the a₂ and b of the rearward, can represent different data, as shown in Fig.2, where ξ is a moveable coordinate.

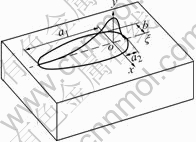
Fig.2 Schematic diagram of surface bielliptic model of heat distribution

2.5 Thermophysical performances parameter of material

Whether the thermophysical performance para- meters of material are correct affects the accuracy of computation results directly. In this paper, the model of the welding pool on TIG welding of T₃ copper plate with thickness of 10 mm was studied. Its thermophysical performance parameters are shown in Table 1.

Table 1 Thermo-physical properties of T₃ red copper

3 Formation of non-uniform grid

Three-dimensional model is utilized to analyze and calculate the heat course of the TIG welding. The calculating grid is shown in Fig.3. Because in the welding course, the temperature gradient of the welding pool which is closed to the heat resource is great, and the changes are especially great, and the farther away from the thermal resource the smaller gradient of the temperature. We can’t solve the contradiction between the computational precision and speed by adopting the uniform grid. The expanding grid in x, y direction was adopted in this paper[16]. The expanding coefficient of the gird is 1.05. But it adopts the thinner uniform grid in z direction.

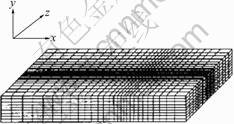
Fig.3 Schematic diagram of non-uniform grid system

4 Calculating results and discussion

Because of the strong arc light interfering during welding and the violent moving of the liquid metal in the welding pool, it is very difficult to measure the temperature field of the welding pool in experiment. So we can prove the exactness by comparing the calculating data value and experimental data value of the melting width and depth during welding. Because the electric arc power of nitrogen is triple of the electric arc power of argon under the same electric current and arc length. We can notably improve the heating effect of the electric arc of argon by mixing a certain proportion of nitrogen. So the mixed protection of argon and nitrogen is applied to the TIG welding in case of no preheating in this experiment. The welding parameters are as follows: the welding electric current is 380 A, the welding speed is 400 mm/min, the flux of Ar gas is 20 L/min, the flux of N₂ gas is 8 L/min, the diameter of the tungsten electrode is 5 mm. Fig.4(a) shows the form of welding pool’s lateral section which obeys above-mentioned parameters, and Fig.4(b) shows the form of its corresponding temperature distribution. Figs.5 and 6 show the changes of weld width and weld depth under different parameters, it is easy to find that the computation results and practical measuring results are well matched, which proves that the model is correct and rational.

4.1 Impact of welding electric current on temperature field

Fig.5 shows the effect of welding current on the heat input. It is easy to find that both the welding width and the welding depth are correspondingly increased with the increasing welding current. The welding linear energy increases correspondingly with the increasing of welding current. The heat input of all positions of the work piece will increase, thus causes the temperature of the work piece to rise up wholly, and the temperature distribution range increases correspondingly.

Fig.4 Cross section image (a) and corresponding temperature distribution (b) of TIG welded joint

Fig.5 Effect of welding current on heat input: (a) Transfor- mation of weld width under different currents; (b) Transfor- mation of weld depth under different currents

4.2 Impact of welding speed on temperature field

Fig.6 shows the effect of welding velocity on the heat input. As shown in Fig.6, both the welding width and the welding depth decrease with the increasing the welding speed. This is based on the situation that the heat inputting of the unit time does not change. The increase of the welding speed shortens the action time in each position of the electric arc and the work piece. The welding heat input decreases in each position of the work piece. Such reasons cause the melting width and the melting depth of the welding pool to decrease.

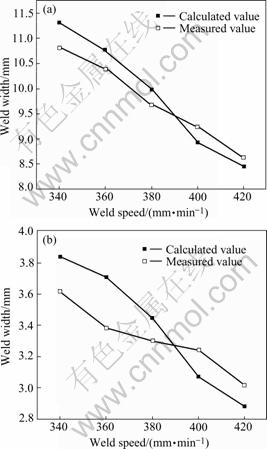
Fig.6 Effect of welding velocity on heat input: (a) Transfor- mation of weld width under different weld speeds; (b) Transfor- mation of weld depth under different weld speeds

 5 Conclusions

1) The surface distribution dual-ellipsoid model of the TIG welding that was treated by the moving electric arc was established. The heat effects of electric arc by mixing the nitrogen of certain proportion in the argon have been notably improved. The experimental results proved that it was feasible to apply the no preheating welding of red copper.

2) The temperature field of the TIG welding with different technical parameters have been calculated, and the relationship between different technical parameters and the melting width and the melting depth were established. The results indicated that the experimental value and the calculated value were well matched, just proved that the model that we set up was correct and rational.

References

[1] LIU Wei, LEI Yu-cheng. Application of neural network in aluminum keyhole plasma welding in vertical position [J]. Journal of Jiangsu University(Natural Science Edition), 2002, 23(4): 68-71.

[2] LI Qiang, QIAN Bai-nian, LI Dian-zhong. Simulation progress of heat transmission and liquid flow for welding pool [J]. Transactions of the China Welding Institution, 2002, 23(4): 91-96.

[3] LI Jing-yong, LI Biao-feng, FENG gang-xian. Effect of weld geometrical features on fatigue properties of 5A30 aluminum alloy welded joints [J]. The Chinese Journal of Nonferrous Metals, 2004, 14(11): 1895-1900.(in Chinese)

[4] GAO Jing-qiang, Wu Chuan-song, LIU Xin-feng. Extracting weld penetration information in TIG welding [J]. The Chinese Journal of Nonferrous Metals, 2004, 12(1): 20-24.(in Chinese)

[5] TSAI M C, SINDO K. Heat transfer and fluid flow in welding arcs produced by sharpened and flat electrodes [J]. Int J Heat Mass Transfer, 1990, 33(10): 2089-2098.

[6] CARMIGNANI C, MARES R, TOSELLI G. Transient finite element analysis of deep penetration laser welding process in a single butt-welded thick steel plate [J]. Computer Methods in Applied Mechanics Engineering, 1999, 179(3): 197-214.

[7] ZHANG Y M, CAO Z N, KOVACEIC R. Numerical analysis of fully penetrated weld pools in gas tungsten arc welding [J]. Journal of Mechanical Engineering Science, 1996, 210: 187-195.

[8] KIM W H, FAN H G, NA S J. Effect of various driving forces on heat and mass transfer in arc welding [J]. Numerical Heat Transfer A, 1997, 32: 633-652.

[9] FAN H G, TSAI H L, NA S J. Heat transfer and fluid flow in a partially or fully penetrated weld pool in gas tungsten arc welding [J]. International Journal of Heat and Mass Transfer, 2001, 44: 417-428.

[10] KIM W H, FAN H G, NA S J. A mathematical of gas tungsten arc welding considering the cathode and the free surface of the weld pool [J]. Metall Mater Trans B, 1997, 28B: 679-686.

[11] USHIO M, WU C S. Mathematical modeling of tree-dimensional heat and fluid flow in a moving gas metal arc weld pool [J]. Metal Mater Trans B, 1997, B28(3): 509-516.

[12] KIM S D, NA S J. Effect of weld pool deformation on weld penetration in stationary gas tungsten arc welding [J]. Weld J, 1992, 71: 179-193.

[13] LIN M L, EAGAR T W. Inflience of arc pressure on weld pool geometry [J]. Weld J, 1985, 64(6): 163-193.

[14] KO S H, CHOI S H, YOO C D. Effect of surface depression on pool convection and geometry in stationary GTAW [J]. Weld Journal, 2001(3): 39-45.

[15] GOLDAK J. A new finite element model for welding heat sources [J]. Metal Trans B, 1984, B15(6): 299-305.

[16] KROLL D R. Finite Difference Equation Calculation of Heat Transfer [M]. Parisian: Allen & Unin, 1982: 45-47.

(Edited by LONG Huai-zhong)

Foundation item: Project(2003AA305970) supported by the Natonal Hi-Tech Research Program of China

Corresponding author: LEI Yu-cheng; Tel: +86-13951282282; E-mail: yclei@ujs.edu.cn