Trans. Nonferrous Met. Soc. China 24(2014) 334-338

Damping properties of as-cast Mg-xLi-1Al alloys with different phase composition

Jing-feng WANG^1,2, Dan-dan XU^1,2, Ruo-peng LU^1,2, Fu-sheng PAN^1,2

1. National Engineering Research Center for Magnesium Alloys, Chongqing University, Chongqing 400044, China;

2. College of Materials Science and Engineering, Chongqing University, Chongqing 400044, China

Received 24 January 2013; accepted 8 May 2013

Abstract: Three kinds of different phases of Mg-xLi-1Al alloys with x=5 (full α LA51), 9 (dual-phase LA91), and 14 (rich-β LA141) were prepared by vacuum melting method. Their microstructure and damping capacities were investigated by optical microscopy, X-ray diffractometry, and dynamic mechanical analysis. The results show that the addition of Li changes the crystal structure of the alloys and causes new damping mechanisms to emerge. And the appearance of BCC structure makes the damping performance improved remarkably. The lower the elastic modulus is, the smaller the strain is and even the slower the acceleration is. The dual-phase alloy shows a better damping capacity while the temperature changes. Furthermore, all three alloys have two significant peaks: P₁ caused by the movement of dislocations on the basal planes and P₂ caused by the sliding of grain boundaries.

Key words: damping; magnesium-lithium alloys; β-Li phase; crystal structure

1 Introduction

Magnesium and magnesium alloys which are usually based on a hexagonal close-packed (HCP) crystal structure are kinds of ultralight alloys. Because of their high strength, hardness, good damping performance and corrosion resistance, they are widely used in the production of mechanical, electronic parts and the field of aviation. However, their plastic deformation ability at room temperature is not so good owing to their HCP structure [1]. The Mg-Li binary phase diagram shows that when BCC-structured lithium is added to magnesium alloy, the HCP structure will change into BCC structure [2]. Magnesium alloy which contents less than 5.7% (mass fraction) of Li has only an HCP-structured α phase of Mg solid solution [3]. With the addition of Li, the crystal structure changes into HCP-structured α phase of Mg solid solution to coexist with a BCC-structured β phase of Li solid solution. When the content of Li reaches 10.3%, only a BCC-structured β phase of Li solid solution can be found [4]. And the density of the alloys (1.738 g/cm³ for Mg and 0.534 g/cm³ for Li) can be reduced, while their processability, ductility, and superplasticity at relatively low stresses can also be improved [5]. Furthermore, low elastic modulus makes plastic deformation easier. Given the low elastic modulus of Li (4.9 GPa), Mg alloy (45 GPa elastic modulus) with Li has a better plastic deformation than others [6]. As the Mg-Li alloys possess the advantages of acceptable mechanical and electrical properties, and even a high heat dissipation and good electromagnetic shield, they have been widely used in engineering designs since the 1960s [7].

The addition of the BCC-structured β-Li phase into the Mg-Li alloys can change its damping capacities, but the mechanism of it receives less attention. As reported, the damping capacities of alloys are dependent on the strain amplitude and related to the dislocation movement in which the dislocations are weakly pinned by impure atoms on the basal planes [8]. The analysis of the influence of the BCC-structured β phase on the damping performance of Mg-Li alloys is a priority.

Al is usually added to strengthen Mg-Li alloys by either dispersion strengthening or age hardening [1]. In the present study, Mg-xLi-1Al alloys with x=5, 9, and 14 were prepared. The current work aims to study the mechanism and effect of the BCC-structured β phase of Li solid solution on the damping performance of Mg-xLi-1Al (x=5, 9, and 14) alloys that have different phase compositions. Based on the experimental results, their damping properties are discussed.

2 Experimental

The chemical compositions of the as-cast Mg-xLi-1Al alloys (mass fraction, %) with x=5.0 (LA51), χ=9.0 (LA91), and χ=14.0(LA141) used in the present study are listed in Table 1.

Table 1 Chemical composition of test alloys

The microstructure and phase information were obtained by optical microscopy (OM) and X-ray diffraction (XRD). The specimens for OM and XRD were prepared according to the standard metallographic procedure with an etching solution consisting of 35 mL alcohol + 5 mL H₂O + 5 mL picric acid + 5 mL acetic acid, for an etching time of 5 s [9], and then etched with 4% HNO₃ in alcohol for an etching time of 10 s. The information on the damping properties was obtained using a dynamic mechanical analyzer (DMA). The specimens for the tests were cut into 40 mm×5 mm from the as-cast plates. The internal friction Q^-1 values of the as-cast Mg-xLi-1Al specimens were measured by TA Q800 DMA equipment (TA Instruments) with a single cantilever at a constant heating rate of 5 °C/min. The testing temperature, frequency, and amplitude were 30 to 300 °C, 1 Hz, and 0.5-300 μm, respectively.

Fig. 1 OM images of as-cast LA51 (a), LA91 (b), and LA141 (c) alloys

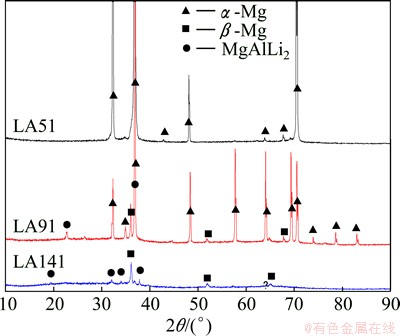
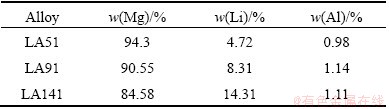
Fig. 2 XRD patterns of as-cast LA51, LA91, and LA141 alloys at room temperature

3 Results and discussion

Figure 1 shows the microstructures of the as-cast LA51, LA91, and LA141 alloys. In the specimens, the white area is the α-Mg phase, whereas the gray area is the β-Li phase. There is only white α-Mg phase observed in LA51 alloy while only gray β-Li phase in LA141 alloy. And the LA91 alloy has about equal half parts in α-Mg and β-Li phases. The area percentages occupied by α and β phases in LA91 alloy are measured using micrometrics SE software for image analysis, and the results are 40.2% in α-Mg and 59.8% in β-Li [9].

Figure 2 shows the XRD patterns of the as-cast Mg-xLi-1Al alloys. Similar to the results mentioned above, both α-Mg and β-Li phases exist in LA91, which is suggested to be the Mg-Li dual-phase alloy. Only α-Mg phase in LA51 and β-Li phase in LA141 are observed. A new MgAlLi₂ phase exists in both LA91 and LA141, indicating that with the increase in Li content, the phases of the alloys change as follows: α-Mg phase→α-Mg+β-Li phase→β-Li phase, separating the MgAlLi₂ phase as its middle compounds.

Figure 3 shows the curve of the damping properties Q^-1 versus the strain amplitudes ε for the as-cast Mg-xLi-1Al alloys measured at 1 Hz constant frequency and 35 °C temperature. The curves indicate that the damping values of the three alloys increase continuously relative to the strain amplitude, with the strain amplitude enhanced from 7.0×10^-6 to 6×10^-3. Under lower strain amplitudes, the damping growth of all the alloys is very slow. However, when the strain amplitude surpasses the critical value, the damping growth begins to accelerate rapidly.

Fig. 3 Q^-1 versus amplitude for as-cast LA51, LA91, and LA141 alloys measured by DMA at 1 Hz and 35 °C (The inset shows magnified curves of three curves of strain-independent part)

The inset in Fig. 3 shows the magnified curves of strain-independent part. The damping properties are augmented with increased Li content under lower strain amplitudes. The damping capacity of LA141, which has only a BCC-structured β-Li phase, is the highest with a damping value close to a high damping standard (Q^-1>0.01) before its critical strain amplitude (ε≈3.5×10^-3). Such phenomena may be caused by the addition of BCC-structured β-Li phase into the HCP-structured α-Mg phase, which expands the slip systems and the gaps between the crystal lattices. Hence, the alloys which have more BCC-structured β-Li phase can more easily emerge through the dislocation motion, and then enhance the damping capacity. The critical strain amplitudes of the three kinds of alloys shown in Fig. 3 also increase as the Li content increases. The situation shows that as more BCC-structured β-Li phases are added into the alloys, more crystal lattices are formed. A number of Li atoms that melt into the alloys accumulate and cause a stronger external force, which is needed when the dislocation escapes the solute atoms. The more difficult the dislocation depinning is, the higher the critical strain amplitude is.

When the strain amplitudes exceed their critical values, the damping capacities change drastically. As shown in Fig. 3, the LA51 alloys which have the lowest damping capacity previously increase sharply when the critical strain amplitude is exceeded, whereas the others show a slight change. The cause of the contrast can be explained by the influence of elastic modulus [6]. Elastic modulus is a physical quantity used to reflect the tensile or compression ability of materials. It is the ratio of the strain and the stress. Hence, given the same amount of stress, the lower the elastic modulus is, the smaller the strain is. Given the elastic modulus of Li of 4.9 GPa, which is about 1/10 of that of Mg, the strain of the alloys with BCC-structured β-Li phase as LA141 and LA91 is smaller than that of LA51 when the critical strain amplitude increases and that of LA141 is still smaller than that of LA91. The same is true for the damping capacity of LA51, which increases sharply, whereas those of the other two increase slightly when the critical strain amplitude is surpassed.

The damping capacity mechanism of the alloys is determined by their dislocation movement, which can be explained through the Granato-Lücke dislocation damping theory [10-13]. Figure 3 is plotted onto a G-L graph (Fig. 4) for further analysis. In the study of the metal damping materials, the G-L curve is usually used to determine whether the damping properties of the materials satisfy the dislocation depinning theory. ln(εQ^-1) and 1/ε are considered, hence, when the damping curve after the critical strain amplitude becomes a straight line, the damping properties of the alloy meet the G-L theory [10,14]. Figure 4 also shows that among three kinds of alloys, only LA51 fits the theory. As both of LA91 and LA141 alloys have BCC-structured β-Li phases but LA51 does not have. It can be inferred that the β-Li phase creates a new damping effect.

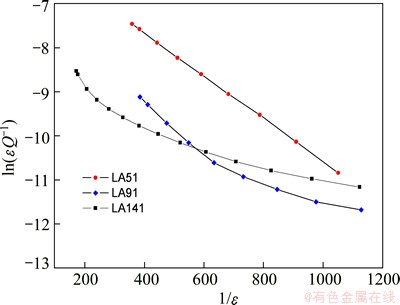
Fig. 4 G-L plot of as-cast LA51, LA91, and LA141 alloys

Figure 5 shows the heating curve of internal friction Q^-1 versus temperature in the range from 30 to 300 °C for the as-cast Mg-xLi-1Al alloys measured at constant strain amplitude of 22 μm under a heating rate of 5 °C/min and with a frequency of 1 Hz. It can be seen in Fig. 5 that the heating Q^-1 curve can be divided into two parts as the changes of damping with the temperature, which means that at a low temperature (below 50 °C) the change of damping with the temperature is inconspicuous while the damping has an increase at a high temperature. In both the two parts, alloys containing BCC-structured β-Li phase as LA91 and LA141 have higher damping value than LA51 which has only HCP-structured α-Mg phase. Also in the low temperature range, LA141 shows a best damping property and even exceeding the high damping standard (Q^-1>0.01). However, in the high temperature part, LA91 curve has a sharp increase and shows the best damping property.

Fig. 5 Q^-1 versus temperature curve for as-cast alloys LA51, LA91, LA141 at 22 μm strain amplitude, 5 °C/min heating rate and 1 Hz frequency

From the reported study [9,15,16], there usually turns up a peak at the low temperature part caused by the sliding of grain boundaries in pure Mg with 99.96% purity (mass fraction), Mg-Ni alloy with 6.2% to 22.6% of Ni, as-annealed Mg-xLi-0.5Zn alloys with x=9.5% and x=10.5%, and as-extruded Mg-11.2Li-0.95Al- 0.43Zn alloys. Because of the initial temperature in this experiment is set at 30 °C, the P₁ peak can be seen clearly in the three kinds of alloys.

The counterintuitive broad P₁ peak of LA141 in the Fig. 5 shows that there must be more than one type of damping systems. At the same time, according to the Granato-Lücke dislocation damping theory [10-13], the damping caused by dislocation movement in the low frequency range can be expressed as follows:

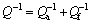                              (1)

in which,

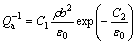                      (2)

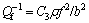                              (3)

where C₁, C₂ and C₃ are the physical constants; ρ is the dislocation density; b is the burgers vector; ε₀ and f are the vibration strain amplitude and frequency, respectively. Dislocation damping is direct proportional to the dislocation density and is related to the strain amplitude and vibration frequency. As temperature rises, the dislocation density gets small, so the contribution of the dislocation damping to the whole damping materials decreases. Therefore, there exist other damping systems after the temperature rises.

Figure 5 also reveals an internal friction peak, P₂, which is at 78 °C in LA51, 102 °C in LA91, and in 165 °C LA141, as indicated by the arrows. The P₂ peak, which is also observed in pure Mg with 99.96% purity, Mg-Ni alloy with 6.2% to 22.6% of Ni, as-annealed Mg-xLi-0.5Zn alloys with x=9.5% and x=10.5%, and as-extruded Mg-11.2Li-0.95Al- 0.43Zn alloys, was reported to be caused by the sliding of grain boundaries [16].

The LA91 curve undergoes a sharp increase after P₂. According to Fig. 2, this phenomenon is caused by the emergence of the MgAlLi₂ phase and the coexistence of HCP and BCC structures. The MgAlLi₂ phase usually exists at grain boundaries at a low temperature, hence, it always blocks slippage. When the temperature rises, the MgAlLi₂ phase dissolves into the matrix, reduces the impurities and the sliding resistance at the grain boundaries, and causes the damping capacity to rise. The phase interface of LA91 increases markedly, and is more likely to generate dislocation because of the coexistence of the HCP and BCC structures. As a result, the increase in the range of the damping capacity in LA91 is much greater than that in the single-phase LA51 and LA141. The illustration further indicates that the addition of BCC-structured β-Li phase is benefit to improve the damping property and this kind of coexistence structure makes alloys a better damping performance.

4 Conclusions

1) The LA51 alloy is rich in α-Mg, whereas LA141 alloy is rich in β-Li phase. The LA91 alloy has two phases in major status and an MgAlLi₂ phase in minor status. They are precipitated along the grain boundaries and in the grains.

2) At room temperature, the addition of BCC-structured β-Li phase into the matrix alloy can promote dislocation motion and enhance the damping capacity before reaching the critical strain amplitude of the alloy. And beyond the critical strain amplitude, the increasing speed of damping properties depends on the elastic modulus. The addition of BCC-structured β-Li phase into the matrix alloy can also change the damping effects from the G-L theory into other unknown ones.

3) All the three kinds of alloys have two peaks in the heating curve: P₁ peak caused by the movement of dislocations on the basal planes, and the P₂ peak caused by the sliding of grain boundaries. Both the curves of LA51 and LA141 undergo a slight change with the increasing temperature, whereas LA91 exhibits a sharp increase attributed to the emergence of the MgAlLi₂ phase and the coexistence of the HCP and BCC structures. The addition of BCC-structured β-Li phase makes the alloys change its damping system and get a better damping performance.

References

[1] CHANG Tien-chan, WANG Jianyih, CHU Chun-len, LEE Shyong, Mechanical properties and microstructures of various Mg-Li alloys [J]. Materials Letters, 2006, 60: 3272-3276.

[2]  Strengthening in Mg–Li matrixcomposites [J]. Composites Science and Technology, 2007, 67: 1965-1973.

[3] LI Ji-qing, QU Zhi-kun, WU Rui-zhi, ZHANG Mi-lin. Effects of Cu addition on the microstructure and hardness of Mg–5Li–3Al–2Zn alloy [J]. Materials Science and Engineering A, 2010, 527: 2780-2783.

[4] ASM Handbook, vol.3: Alloy phase diagrams [M]. Ohio: ASM Int’l, 1992.

[5] HAFERKAMP H, BOEHM R, HOLZKAMP U, JASCHIK C, KAESE V, NIEMEYER M. Alloy development, processing and applications in magnesium lithium alloys [J]. Materials Trans, 2001, 42: 1153-1331.

[6] NOBLE B, HARRIS S J, DINSDALE K. The elastic modulus of aluminium-lithium alloys [J]. Materials Science, 1982, 17: 461-468.

[7] SMITH W F. Structure and properties of engineering alloys [M]. Singapore: McGraw Hill, 1993: 557.

[8] SUGIMOTO K, NIIYA K, OKAMOTO T, KISHITAKE K. Effect of crystal orientation on amplitude-dependent damping in magnesium [J]. Trans JIM, 1975, 16: 647.

[9] WU S K, CHANG S H, CHOU T Y, TONG S. Low-frequency damping properties of dual-phase Mg–xLi–0.5 Znalloys [J]. Journal of Alloys and Compounds, 2008, 465: 210-215.

[10] WANG Jing-feng, SONG Peng-fei, GAO Shan, HUANG Xue-fei, SHI Z Z, PAN F S. The Y-doped MgZnCa alloys with ultrahigh specific strength and good corrosion resistance in simulate body fluid [J]. Materials Science Engineering A, 2011, 528(18): 5914-5920.

[11] GRANATO A, LUCKE K. Theory of mechanical damping due to dislocations [J]. Applied Physics, 1956, 27: 583-593.

[12] MAYENCOURT C, SCHALLER R. Mechanical-stress relaxation in magnesium-based composites [J]. Materials Science Engineering A, 2002, 325: 286-291.

[13] GRANATO A, LUCKE K.Application of dislocation theory to internal friction phenomena at high frequencies [J]. Applied Physics, 1956, 27: 789-805.

[14] ZHANG Zhen-yan, ZENG Xiao-qin, DING Wen-jiang. The influence of heat treatment on damping response of AZ91D magnesium alloy [J]. Materials Science Engineering A, 2005, 392: 150-155.

[15] CHANG S H, WU S K, TSAI W L, BOR H Y. Low-frequency damping properties of as-extruded Mg-11.2Li-0.95Al-0.43Zn magnesium alloys [J]. Materials Science Engineering A, 2011, 528: 6020-6025.

[16] HU Xiao-shi, ZHANG Yong-kun, ZHENG Min-yi, WU Kun. A study of damping capacities in pure Mg and Mg-Ni alloys [J]. Scripta Materialia, 2005, 52: 1141-1145.

不同相组成铸态Mg-xLi-1Al合金的阻尼性能

王敬丰^{1, 2}，徐丹丹^1,2，鲁若鹏^1,2，潘复生¹

1. 重庆大学 国家镁合金材料工程技术研究中心，重庆 400044；

2. 重庆大学 材料科学与工程学院，重庆 400044

摘  要：采用真空熔炼法制备三种不同相态的Mg-xLi-1Al三元合金，并使用光学显微镜、X射线衍射分析及动态力学分析仪研究其显微组织及阻尼性能。结果表明：由于锂含量的增加，合金的相结构发生转变且出现新的阻尼机制，其中BCC结构的出现使阻尼性能显著提高，同时弹性模量的减小也使临界应变振幅值降低。两相共存状态的合金随温度变化表现出较高的阻尼现象，并在低温与高温区均出现两个较为明显的峰值，其中低温区的P₁峰是位错阻尼峰，高温区的P2峰是晶界阻尼峰。

关键词：阻尼；镁锂合金；β-Li相；晶体结构

(Edited by Chao WANG)

Foundation item: Project (NCET-11-0554) supported by the Program for New Century Excellent Talents in University, China; Project (2011BAE22B04) supported by the National Key Technology R&D Program, China; Project (51271206) supported by the National Natural Science Foundation of China

Corresponding author: Jing-feng WANG; Tel/Fax: +86-23-65112153; E-mail: jingfengwang@163.com

DOI: 10.1016/S1003-6326(14)63065-X