Calculation of temperature distribution in adiabatic shear band based on gradient-dependent plasticity
WANG Xue-bin(王学滨)
(Department of Mechanics and Engineering Sciences, Liaoning Technical University, Fuxin 123000, China)
Abstract: A method for calculation of temperature distribution in adiabatic shear band is proposed in terms of gradient-dependent plasticity where the characteristic length describes the interactions and interplaying among microstructures. First, the increment of the plastic shear strain distribution in adiabatic shear band is obtained based on gradient-dependent plasticity. Then, the plastic work distribution is derived according to the current flow shear stress and the obtained increment of plastic shear strain distribution. In the light of the well-known assumption that 90% of plastic work is converted into the heat resulting in increase in temperature in adiabatic shear band, the increment of the temperature distribution is presented. Next, the average temperature increment in the shear band is calculated to compute the change in flow shear stress due to the thermal softening effect. After the actual flow shear stress considering the thermal softening effect is obtained according to the Johnson-Cook constitutive relation, the increment of the plastic shear strain distribution, the plastic work and the temperature in the next time step are recalculated until the total time is consumed. Summing the temperature distribution leads to rise in the total temperature distribution. The present calculated maximum temperature in adiabatic shear band in titanium agrees with the experimental observations. Moreover, the temperature profiles for different flow shear stresses are qualitatively consistent with experimental and numerical results. Effects of some related parameters on the temperature distribution are also predicted.
Key words: nonuniform temperature; adiabatic shear band; shear strain localization; gradient-dependent plasticity; plastic shear strain distribution CLC number: TG113
Document code: A
1 INTRODUCTION
It is well known that the excellent strength-to-mass ratio and fracture resistance make titanium and titanium alloys very attractive to aerospace applications. Shear localization is an important and often dominating deformation and failure mechanism for titanium and titanium alloys in dynamic loadings[1-12]. Prior to the onset of shear localization, the deformation can be approximately considered to be uniform. Once the shear localization is initiated, the intense localized shear deformation is accumulated progressively in narrow band that is called shear band or localized band. The eventual outcome of localized deformation is ductile rupture and material separation. Shear localization occurs and plays an important role in engineering applications. For example, shear bands can be observed in ballistic impact, explosive fragmentation, high speed machining, metal forming, grinding, interfacial friction, powder compaction, granular flow, and seismic event.
It is well known that intensive shear deformation is concentrated in adiabatic shear band in titanium and titanium alloys under dynamic loadings and the band thickness for Ti is approximately 10-20μm[1,3]. For Ti-6Al-4V, the measured width of the shear bands ranges from 12 to 55μm[13]. Besides, many experimental observations and numerical simulations show that there is a nonuniform temperature distribution in adiabatic shear band[13-18]. It is shown that the measured temperature distribution in adiabatic shear band is a function of time and position and a peak temperature of 440-550℃ is found in the various tests[13]. The numerical simulation shows that while most of the material in adiabatic shear band is at temperatures about 250℃, maximum temperature reaches over 850℃[14]. Measured results show that shear bands in two kinds of steels are relatively wide, that the maximum temperature rise in the band is about 450℃ and that the temperature distribution across the band is consistent with results of stability analyses[15].The local temperature in the shear band is measured[16], within the shear band region, temperatures of 600℃ have been found. The numerical results show that there is a nonuniform temperature distribution in adiabatic shear band[17]. Moreover, it is indicated that temperature distribution in the shear band has periodic patterns in both space and time[17].
Interactions and interplaying among microstructures are of very importance for Ti and Ti alloy and have been studied extensively by experiments[19-22]. For Ti and Ti alloy the texture is heterogeneous to some extent and a certain microstructure will be influenced significantly by its neighborhoods. The characteristic length in gradient-dependent plasticity, which depends on the mean grain diameter, governs the extent of long-range interaction.
According to gradient-dependent plasticity[23-25], shear localization in linear strain-softening heterogeneous material under uniform shear and static loading was investigated analytically by Wang et al[26]. Based on the same theory, analysis of localized characteristics of deformation in titanium subjected to nonuniform shear stress in the process of shear band propagation was carried out by Wang et al[27]. However, the thermal softening at high strain rates is ignored completely in previous analyses[26, 27]. Beside the shear localization of ductile metal materials, gradient-dependent plasticity has been applied into tensile localization of low-carbon steel[28, 29].
The distribution of tempreture cannot be interpreted or predicted in terms of traditional elastoplatic theory where flow stress only depends on the plastic strain rather than the plastic strain gradient. In the present paper, the nonuniformity of tempreture in adiabatic shear band in the strain-softening process is studied.
2 THEORETICAL ANALYSIS AND PROCEDURE OF CALCULATION
2.1 Mechanical model and constitutive relation
The model of shear localization that we shall consider is depicted in Fig.1. It is a specimen with a certain height that is loaded in shear stress in the horizontal direction(i.e. x-axis) and compressive
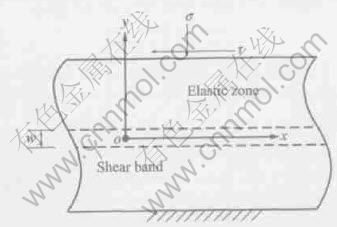
Fig.1 Shear strain localization of specimen and well-developed adiabatic shear band
constant stress σ in vertical direction. For simplicity, the lower end of the block is fixed(i.e. the horizontal and the vertical displacements of the end are zero). An important outcome of shear localization is the decrease of the load-carrying capability of the block, so it can be supposed that localization is initiated at the peak stress and that the shear deformation only occurs in the horizontal direction.
Some experimental results show that the post-peak behavior of Ti or Ti alloy under dynamic loadings exhibits approximately linear strain-softening[6,13], so the constitutive relation in strain-softening stage can be seen as a descending line whose absolute value of the slope is called dynamic shear softening modulus, see Fig.2.
Fig.2 Dynamic strain-softening constitutive relation
2.2 Analytical solution of plastic shear strain distribution
To consider the effects of strain softening and strain rate, herein the Johnson-Cook constitutive law[13, 30] that is semi-empirical in nature is adopted:
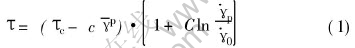
where τc is the shear strength;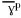 
is the average plastic shear strain; c is the static softening modulus; C is a material constants; 
p is the average shear strain rate and 0 is the average shear strain rate under quasi-static conditions.
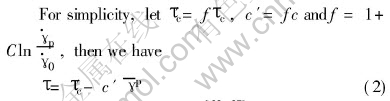
According to Wang et al[23, 27], based on gradient-dependent plasticity the plastic shear strain distribution γp(y) in adiabatic shear band and the thickness w of the band can be given as, respectively
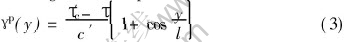
w=2πl(4)
where l is the characteristic length of material and is usually concerned with average granular diameter of heterogeneous material.
2.3 Increment of temperature distribution
According to Eq.(3), increment Δγp(y) of the plastic shear strain distribution over any time interval [t, t+Δt] can be expressed as
where Δτ=τt-τt+Δt is the increment of flow shear stress in strain-softening stage; τt and τt+Δt are the flow stresses at time t and t+Δt, respectively. For simplicity, Δτ can be considered to be a constant, thus Δγp(y) is the same for any time step.
Due to the fact that Δγp(y) depends on the coordinate y, the plastic work in adiabatic shear band is certainly nonuniform. The plastic work increment distribution ΔW(y) over the interval[t, t+Δt] can be calculated as
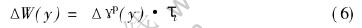
It is well known that approximately 90% plastic work is converted to heat and that the increment of temperature is dependent on the mass density ρ and the heat capacity per unit mass cp, namely
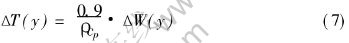
where ΔT(y) is the increment of temperature distribution in adiabatic shear band.
It should be noted that the present expression for the increment of temperature distribution is different from that for usually average temperature expressed as
The main difference is that the present formulation, i.e., Eq.(7), is applicable to any position in adiabatic shear band; however, the previous expression, namely, Eq.(8), can be used to calculate the change in average temperature.
To assess the average temperature increment ΔT in adiabatic shear band over the interval [t, t+Δt], Eq.(8) needs to be modified as
The increment Δγ[TX-*4]p can be determined according to Eq.(2) as follows:
Substitution of Eq.(10) into Eq.(9) yields
At time [t, t+Δt], the actual average temperature is
where Tt is the average temperature at time t.
Similarly, at the end of the interval, the actual average plastic shear strain is
where 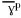is the average plastic shear strain at time t.
To obtain the decrease of flow shear stress due to heat softening effect, Johnson-Cook constitutive relation is used,
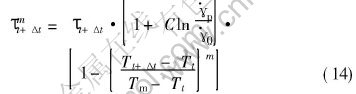
where Tm is the melting temperature of material; T0 is the initial temperature of material.
The shear stress τmt+Δt is believed to be the actual flow shear stress caused by the heat generated by plastic shear, which wakening the load-carrying capacity of the material. Substituting τmt+Δt into Eq.(6) for τt and using Eq.(7) to Eq.(14), then we can calculate the increment of the temperature distribution over the next time interval [t+Δt, t+2Δt]. Summing the temperature distribution increments in each time step leads to change in the total temperature distribution. When shear localization just occurs, t=0, Tt=T0, τ0=τc, 0=0.
2.4 Process of calculation
The schematic figure for calculation process is depicted in Fig.3.
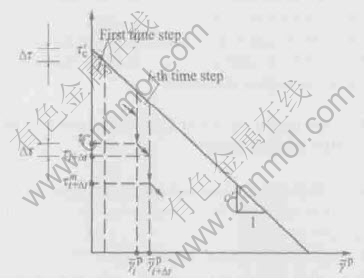
Fig.3 Calculation of flow shear stress within any time step
The main steps for calculation of temperature distribution in adiabatic shear band are outlined as follows.
Firstly, it is assumed that the total time from occurrence of shear localization to final fracture is tm. Divide tm into finite time intervals n, tm=nΔt, for example the first interval is [0, Δt] and any interval is [t, t+Δt]. For the sake of simplicity, decrease of flow shear stress Δt during the ith time step remains a constant. At the start of the first time step t=0, Tt=T0, τ0=τc and 0=0, where T0 is the initial temperature of material.
Secondly, gradient-dependent plasticity is adopted to compute the increment of the plastic shear strain distribution in adiabatic shear band according to Δτ. The flow shear stress τt at time t is called the old flow shear stress that is needed to calculate the nonuniform plastic work in the next step.
Thirdly, the old flow shear stress is multiplied by the obtained plastic shear strain distribution increment to calculate the change in the nonuniform plastic work. According to the well-known assumption that 90% plastic work is converted into heat, the increment of the temperature distribution in adiabatic shear band is proposed.
Next, Integrating the temperature distribution leads to the change in the average temperature. Using Johnson-Cook constitutive relation, a new flow shear stress due to thermal softening is presented. The old flow shear stress in the third step is replaced by the present new flow shear stress. Recalculate the plastic work distribution, the temperature distribution and the average temperature over the following interval. Continue the procedure above until the average plastic shear strain at failure is achieved.
Once the total time tm is consumed, summing the increments of temperature distribution in each interval results in the total increase of temperature in adiabatic shear band.
3 EXAMPLES AND DISCUSSION
According to Ref.[13], the dynamic shear strength, the mess density, the melting temperature and the heat capacity per unit mass for Ti-6Al-4V are τ′c=fτc, ρ=4428kJ/m3, Tm=1923K, and cp=564J/(kg·K), respectively. The experimentally obtained shear band thickness in Ti-6Al-4V is about 12-55μm[13], so we let the thickness of shear band w=35μm. Using Eq.(4), the characteristic length describing the extent of heterogeneity for Ti-6Al-4V is about l=5.57μm. The initial temperature is T0=293K and softening modulus c′=111.6MPa=cf is selected to describe the brittleness of Ti-6Al-4V. In addition, for simplicity, we set m=1.
The temperature distributions for different average plastic shear strains in adiabatic shear band in Ti-6Al-4V are shown in Fig.4. It is found that the temperature distribution is highly nonuniform. As expected, temperature approaches to its maximum at the center of the band and decreases to zero at the two external edges. Temperature profiles become steeper when the average plastic shear strain is increased. In a word, the amount of heat generation is the highest at the sites of the highest plastic shear strain.
When the flow shear stress is decreased to 400MPa corresponding to the average plastic shear strain of 1.8, from the peak stress, the calculated peak temperature 760K(=487℃) in the middle of the band falls into the experimentally measured range of 450-550℃[13]. The shaded region in Fig.4 denotes the temperature range measured by an array of infrared detectors[13]. Therefore, the present prediction for the maximum temperature in adiabatic shear band is in agreement with experimental measurements.
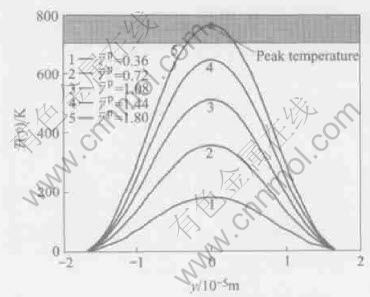
Fig.4 Temperature distributions in adiabatic shear band for different average plastic shear strains
Fig.5 depicts the increments of the nonuniform temperature in adiabatic shear band for different average plastic shear strains. It can be found that for the lower average plastic shear strain the temperature distribution grows more quickly than
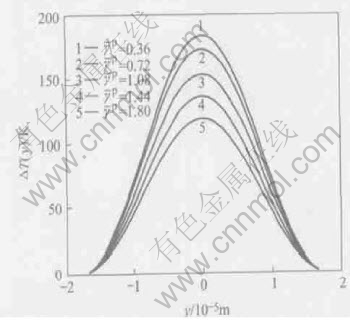
Fig.5 Increments of temperature distribution in adiabatic shear band for different average plastic shear strains
that for the higher average plastic shear strain. This is due to the fact that the plastic work becomes low as the average plastic shear strain increases.
Effects of the dynamic softening modulus c′ and the parameter 0.9(ρcp)-1 on the temperature profiles are shown in Figs.6 and 7. In Fig.6, we take τ′c=750MPa, ρ=4428kg/m3, Tm=1923K, cp=564J/(kg·K), w=35μm, T0=293K, γp=0.36, and m=1. In Fig.7, we let τ′c=750MPa, Tm=1923K, w=35μm, T0=293K, γp=0.36, m=1, and c′=111.6MPa.
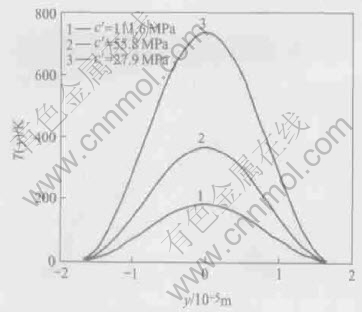
Fig.6 Temperature distributions in adiabatic shear band for different dynamic shear softening modulus
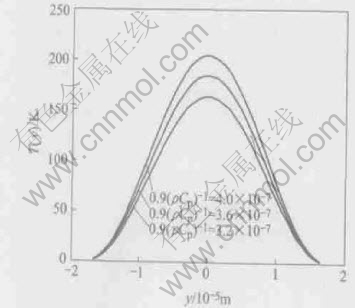
Fig.7 Temperature distributions in adiabatic shear band for different densities of mass multiplied by heat capacities per unit mass
It is found that the lower the softening modulus is, the higher the nonuniform temperature is; the temperature is increased as ρcp is decreased. Low heat capacity makes Ti-6Al-4V prone to increase of temperature in shear band, so that Ti-6Al-4V shows a great propensity for adiabatic shear band formation.
The present theoretical results for nonuniform temperature distributions qualitatively agree with previous numerical and experimental results showing that the temperature is a function of position and time[11,13].
4 CONCLUSIONS
1) It is necessary to generalize or modify the traditional elastoplastic theory to investigate the characteristics of temperature distribution in adiabatic shear band, which can be observed in many experimental tests.
2) Gradient-dependent plasticity is unitized to calculate the increment of plastic strain distribution, the increment of plastic work and the increment of temperature distribution within any time step. Consequence of the increase of the average temperature in adiabatic shear band is the decrease of the load-carrying capacity, which is computed according to the Johnson-Cook constitutive relation.
3) Present calculations of the temperature distribution in adiabatic shear band show that the maximum temperature is reached at the center of the band, while at the two edges of the band there is not any temperature change. The value of the present peak temperature in adiabatic shear band in Ti-6Al-4V is consistent with experimental observations. Moreover, the obtained highly nonuniform temperature profiles agree with existing experimental measurements and numerical predictions.
4) It should be noted that the present analysis is particularly applicable to the high strain rate tests, for heat diffusion is completely neglected.
REFERENCES
[1]Nesterenko V F, Meyers M A, Wright T W. Self-organization in the initiation of adiabatic shear bands [J]. Acta Mater, 1998, 46(1): 327-340.
[2]Xu Y B, Zhong W L, Chen Y J. Shear localization and recrystallization in dynamic deformation of 8089 Al-Li alloy [J]. Materials Science and Engineering A, 2001, A299(1-2): 287-295.
[3]Xue Q, Meyers M A, Nesterenko V F. Self-organization of shear bands in titanium and Ti-6Al-4V alloy [J]. Acta Materialia, 2002, 50(3): 575-596.
[4]YU Jin-qiang, ZHOU Hui-hua, SHEN Le-tian. Thermo-plastic shear bands induced during dynamic loading in Ti-55 alloys [J]. Acta Metallurgica Sinica, 1999, 35(4): 379-383. (in Chinese)
[5]LIU Wen-sheng, HUANG Bai-yun, HE Yue-hui. The room-temperature fracture mechanics of a fully-lamellar TiAl alloy [J]. J Cent South Univ Technol, 1997, 28(2): 152-155.(in Chinese)
[6]LI Qiang, XU Yong-bo, SHEN Le-tian. Dynamic mechanical properties and damage characteristics of titanium alloy (Ti-17) [J]. Acta Metallurgica Sinica, 1999, 35(5): 491-494. (in Chinese)
[7]YANG Yang, CHENG Xin-lin, LI Zheng-hua. Effects of Metallurgical factors on the forming of adiabatic shear band [J]. Rare Metal and Materials and Engineering, 2003, 32(4): 261-263.(in Chinese)
[8]YANG Yang, WANG Zhao-ming, ZHANG Shao-rui. Some metallurgical behaviours of adiabatic shear band on Ti side in the Ti/mild steel explosive cladding interface [J]. Rare Metal and Materials and Engineering, 1997, 26(4): 13-17. (in Chinese)
[9]Tamizifar M, Omidvar H, Salehi S M T. Effect of processing parameters on shear bands in non-isothermal hot forging of Ti-6Al-4V [J]. Materials Science and Technology, 2002, 18(1): 21-29.
[10]YANG Yang, CHENG Xin-lin. Current status and trends in researchers on adiabatic shearing [J]. The Chinese Journal of Nonferrous Metals, 2002, 12(3): 401-408. (in Chinese)
[11]Bai Y, Bodd B. Adiabatic Shear Localization [M]. Oxford: Pergamon Press, 1992.
[12]Shawki T G, Clifton R J. Shear band formation in thermal viscoplastic materials [J]. Mechanics of Materials, 1989, 8(1): 13-43.
[13]Liao S C, Duffy J. Adiabatic shear bands in a Ti-6Al-4V titanium alloy [J]. J Mech Phys Solids, 1998, 46(11): 2201-2231.
[14]Roessig K M, Mason J J. Adiabatic shear localization in the dynamic punch test, part Ⅱ: numerical simulations [J]. International Journal of Plasticity, 1999, 15(3): 263-283.
[15]Hartley K A, Duffy J, Hawley R H. Measurement of the temperature profile during shear band formation in steels deforming at high strain rates [J]. Journal of the Mechanics and Physics of Solids, 1987, 35(3): 283-301.
[16]Duffy J, Chi Y C. On the measurement of local strain and temperature during the formation of adiabatic shear bands [J]. Materials Science and Engineering A, 1992, 157(2): 195-210.
[17]LI Shao-fan, LIU Wing-Kam, QIAN Dong, et al. Dynamic shear band propagation and micro-structure of adiabatic shear band [J]. Comput Methods Appl Mech Engrg, 2001, 191(1-2): 73-92.
[18]Wang Y M, Batra R C. Effect of kinematic hardening on the initiation and growth of shear bands in plane strain deformations of thermoviscoplastic solid [J]. Acta Mechanica, 1994, 102(1-4): 217-233.
[19]WANG Jian-hua, YI Dan-qing, WANG Bin. Microstructure and properties of 2618-Ti heat resistant aluminum alloy [J]. Trans Nonferrous Met Soc China, 2003, 13(3): 590-594.
[20]SHANG Jun-ling, LI Bang-sheng, GUO Jing-jie. Microstructure evolution during preparation of in-situ TiB reinforced titanium matrix composites [J]. Trans Nonferrous Met Soc China, 2003,1 3(2): 315-319.
[21]WANG Hao, FU Zheng-yi, GU Ping. Mechanical properties and microstructure of TiB2 ceramic influenced by ZrB2 additive [J]. Trans Nonferrous Met Soc China, 2002,12(5): 904-908.
[22]SUN Feng, LIN Dong-liang. Microstructure evolution in a large-grained TiAl alloy [J]. Trans Nonferrous Met Soc China, 2002, 12(4): 615-620.
[23]WANG Xue-bin, YANG Xiao-bin, ZHANG Zhi-hui, et al. Dynamic analysis of fault rockburst based on gradient-dependent plasticity and energy criterion [J]. Journal of University of Science and Technology Beijing, 2004, 11(1): 5-9.
[24]WANG Xue-bin, DAI Shu-hong, HAI Long, et al. Quantitative calculation of dissipated energy of fault rock burst based on gradient-dependent plasticity [J]. Journal of University of Science and Technology Beijing, 2004, 11(3): 197-201.
[25]WANG Xue-bin, PAN Yi-shan. Effect of relative stress on post-peak uniaxial compression fracture energy of concrete [J]. Journal of Wuhan University of Technology-Materials Science Edition, 2003,18(4): 89-92.
[26]WANG Xue-bin, DAI Shu-hong, HAI Long, et al. Analysis of localized shear deformation of ductile metal based on gradient-dependent plasticity [J]. Trans Nonferrous Met Soc China, 2003, 13(6): 1348-1353.
[27]WANG Xue-bin, YANG Mei, YU Hai-jun, et al. localized shear deformation during shear band propagation in titanium considering interactions among microstructures [J]. Trans Nonferrous Met Soc China, 2004,14(2): 335-339.
[28]WANG Xue-bin, YANG Mei, PAN Yi-shan. Analysis of necking under condition of uniaxial tension of low-carbon steel specimen based on gradient-dependent plasticity [J]. Journal of Plasticity Engineering, 2002, 9(3): 55-57. (in Chinese)
[29]WANG Xue-bin, YANG Mei, PAN Yi-shan. Analysis of size effect in uniaxial tension for low-carbon steel specimen considering strain gradient effect [J]. Journal of Mechanical Strength, 2003, 25(4): 463-465. (In Chinese)
[30]Johnson G R. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures [J]. Engineering Fracture Mechanics, 1985, 21(1): 31-48.
(Edited by PENG Chao-qun)
Foundation item: Project(50309004) supported by the National Natural Science Foundation of China
Received date: 2004-02-01; Accepted date: 2004-06-25
Correspondence: WANG Xue-bin, PhD; Tel: +86-418-3351351; E-mail: wxbbb@263.net
