DOI: 10.11817/j.issn.1672-7207.2016.03.005
2Cr12NiMo1W1V超临界钢高温流变应力模型及热加工图
王梦寒,陈明亮,王瑞,王根田
(重庆大学 材料科学与工程学院,重庆,400030)
摘要:为研究2Cr12NiMo1W1V超临界马氏体不锈钢的高温变形行为,对其进行热压缩试验,得到其在变形温度为1 123~1 373 K,应变速率为0.005~5 s-1的真应力-真应变曲线,对流变应力特征进行研究,分析其高温变形的物理本质。采用Zener-Hollomon参数法构建动态材料模型(DMM),以热压缩试验为基础,建立不同应变下的热加工图。根据变形稳定阶段的热加工图确定该马氏体不锈钢热变形的失稳区和安全区。研究结果表明:采用该合金的高温塑性变形本构模型所得预测值与实验值拟合程度高,表明该合金在热变形过程中的流变应力可用构建的双曲正弦本构模型来描述;热加工图受变形量影响较大,当变形较小时,安全区随着应变增加而发生迁移,变形进入稳定阶段后,安全区保持恒定;在低温高应变区(温度为1 200~1 280 K,应变速率为1~5 s-1)以及高温低应变区(温度为1 320~1 400 K,应变速率为0.1~0.3 s-1)这2个区域为变形安全区,适合2Cr12NiMo1W1V超临界马氏体不锈钢进行热加工。
关键词:超临界马氏体不锈钢;本构模型;热加工图
中图分类号:TG146.2 文献标志码:A 文章编号:1672-7207(2016)03-0741-08
High temperature flow stress model and hot processing map for 2Cr12NiMo1W1V supercritical steel
WANG Menghan, CHEN Mingliang, WANG Rui, WANG Gentian
(College of Materials Science and Engineering, Chongqing University, Chongqing 400030, China)
Abstract: In order to study the high temperature deformation behavior of 2Cr12NiMo1W1V supercritical martensitic stainless steel, the true stress-strain curves from thermal compression test was studied to get the intrinsic properties at the temperature of 1 123-1 373 K, and the strain rate of 0.005-5 s-1. The constitutive model of the steel at elevated temperature was obtained by introducing Zener-Hollomon parameter, and the good agreement between the predicted and experimented values confirm that flow stress in the thermal deformation can be described by the hyperbolic sine constitutive equation. The processing maps in the case of different true strains based on dynamic material model and the experiment were analyzed. The results show that the hot processing maps are greatly influenced by strain, and the safety zone migrates with the increase of strain when the deformation is small, and keeps constant when the deformation is steady. The instability and safety zones of thermal deformation can also be recognized by the maps in stable stage, and the region of low temperature and high strain rate (temperature of 1 200-1 280 K, strain rate of 1-5 s-1), and region of high temperature and low strain rate (temperature of 1 320-1 400 K, strain rate of 0.1-0.5 s-1) are the safty zones, which are suitable for deformation of 2Cr12NiMo1W1V supercritical martensitic stainless steel.
Key words: supercritical martensitic stainless steel; constitutive model; hot processing map
为了减少环境污染,提高火电汽轮机的热效率,研发高效、低耗、节能的超临界、超超临界汽轮机发电机组成为火电行业发展的重要趋势[1]。由于超临界与超超临界机组零件的工作环境恶劣,因此,要求使用高温性能更好的材料[2]。2Cr12NiMo1W1V超临界马氏体不锈钢是在12% Cr系马氏体不锈钢的基础上加入Ni,Mo,V和W等合金元素冶炼而成[3],不仅具有Cr12型马氏体不锈钢抗氧化、抗腐蚀性能,而且具有组元弥散带来的热强化、热稳定性能以及较好的综合力学性能,是在300 MW汽轮机组中广泛使用的超临界钢,主要用于制造汽轮机动叶片、缸体、转子等零件,对于超临界汽轮机的发展具有重要作用[4-5]。目前,国内对于2Cr12NiMo1W1V超临界马氏体不锈钢的研究主要集中在冶炼和热处理方面。罗通伟等[6]对2Cr12NiMo1W1V等12%Cr型叶片钢热轧生产工艺进行了研究,提出了控制钢中δ-铁素体的措施;DEGUCHI等[7-8]对超临界马氏体不锈钢的锻后热处理工艺进行了改进。目前,关于2Cr12NiMo1W1V超临界马氏体不锈钢成形性能的相关研究鲜有报道,由于技术保密,国外相关的研究报道也较少。为了明晰该材料的高温变形行为,本文作者对2Cr12NiMo1W1V超临界马氏体不锈钢进行热压缩试验,通过建立材料的双曲正弦本构模型及基于动态材料模型(DMM)的热加工图,研究温度、应变速率等参数对该不锈钢材料高温塑性变形的影响,以便为2Cr12NiMo1W1V钢塑性成形的有限元模拟和热加工工艺的制定提供必要的实验数据和理论参考。
1 材料及实验方法
热模拟压缩试样采用热轧淬火态2Cr12NiMo1W1V马氏体不锈钢,试样切割成直径×高为8 mm×12 mm的圆柱体,并打磨光滑,在Gleeble-1500热模拟试验机上进行单向等温压缩实验。试样压缩前以10 K/s的加热速率加热到1 523 K,保温3 min,得到均匀的奥氏体组织;然后以5 K/s速率降温至变形温度,保温10 s以消除试样内部的温度梯度,减少变形误差。随后,试样在不同温度下以不同的应变速率进行等温压缩变形。单向热压缩实验的变形温度分别为1 123,1 173,1 273和1 373 K,应变速率分别为0.005,0.05,0.5和5 s-1,最大真应变为0.7。为了减小摩擦对应力状态的影响,得到准确的实验结果,在试样两端涂覆润滑剂并加贴了钽片。
2 实验结果与分析
2.1 热变形流变曲线
对热压实验结果进行处理后,获得如图1所示的2Cr12NiMo1W1V钢在不同应变率条件下的真应力-真应变曲线。由图1可知:2Cr12NiMo1W1V钢热压缩变形时,流变应力变化趋势基本一致;在变形初期,流变应力随着应变的增大而迅速增大。这是因为该阶段外加应力使位错密度增大,并发生了交割缠结,位错滑移受到阻碍;而变形程度较低时,晶内储存能较小,只发生了少量的动态回复,加工硬化作用远大于软化作用;随着变形量增加,流变应力增大速度减小,逐渐趋于稳定。这是由于位错密度继续增大,位错的滑移和攀移逐渐发生,在变形激活能作用下,动态回复尤其是动态再结晶的作用也加强,加工硬化与动态回复、动态再结晶软化逐渐达到动态平衡,进入稳态变形阶段,此时真应力-真应变曲线趋于平直。
2Cr12NiMo1W1V钢流变应力还受温度和应变速率的影响。当应变速率一定时,随着温度升高,真应力降低。这是由于温度升高,金属原子热振动的振幅增大,原子间的相互作用减弱,原子的扩散速度加快,位错滑移阻力减小,且新的滑移系不断产生,使动态再结晶能够快速进行,更快地抵消加工硬化。变形温度越高,合金的动态软化能力越强,流变应力增加越慢,流变应力峰值越小。当温度一定时,随着应变速率的增加,真应力增加。这是由于随着变形速率的增加,变形时间减少,位错密度在短时间内急剧增加,而再结晶来不及充分进行,动态软化作用弱于硬化作用,流变应力不断升高。2Cr12NiMo1W1V超临界马氏体不锈钢流变应力峰值随应变速率增大而增大,是一种正应变速率敏感材料。当应变速率较高时,合金在短时间内产生大量的变形能,当变形达到一定程度时,热量累积引发绝热效应,压缩变形发生失稳,使得流变应力曲线出现震荡特征,如图1(d)所示。此外,当应变速率为5 s-1时,流变应力曲线还出现锯齿状特性。这是因为在高应变速率下,合金的变形快,位错的急剧增大导致合金发生不连续动态再结晶,动态再结晶引起的软化与再结晶晶粒的变形引起的硬化交替进行,流变曲线出现周期性类似锯齿状的流变特征。
2.2 流变应力本构模型
金属和合金的热加工变形是一个受热激活能控制的过程,其流变行为可用流变应力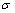 、应变速率
、应变速率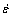 和变形温度T三者之间的相互关系可用SELLARS等提出的包含变形激活能和温度T的双曲正弦形式的修正Arrhenius关系来描述[9-10]:
和变形温度T三者之间的相互关系可用SELLARS等提出的包含变形激活能和温度T的双曲正弦形式的修正Arrhenius关系来描述[9-10]:
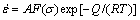 (1)
(1)
在不同的应力水平,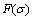 有3种不同的表现形式:
有3种不同的表现形式:
低应力水平(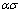 <0.8)时,
<0.8)时,
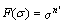 (2)
(2)
高应力水平(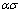 >1.2)时,
>1.2)时,
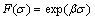 (3)
(3)
在所有应力水平下,
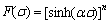 (4)
(4)
其中:A,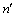 ,n,
,n,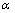 和
和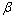 为与温度无关的常数,且
为与温度无关的常数,且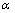 ,
,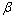 和应力指数n之间满足
和应力指数n之间满足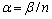 ;
;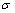 为流变曲线峰值应力(MPa);R为摩尔气体常数(8.314 J/(mol·K));T为变形温度(K);Q为变形激活能(kJ/mol),反映了材料热变形的难易程度。分别将式(2)~(4)代入式(1)并取对数,得到:
为流变曲线峰值应力(MPa);R为摩尔气体常数(8.314 J/(mol·K));T为变形温度(K);Q为变形激活能(kJ/mol),反映了材料热变形的难易程度。分别将式(2)~(4)代入式(1)并取对数,得到:
 (5)
(5)
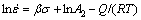 (6)
(6)
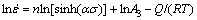 (7)
(7)
由式(5)和式(6)可知:当温度一定时, 分别与
分别与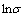 和
和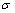 呈线性关系,而
呈线性关系,而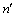 和
和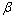 为曲线
为曲线 -
-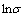 和
和 -
-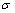 的斜率。根据2Cr12NiMo1W1V钢热压缩实验结果,绘制出
的斜率。根据2Cr12NiMo1W1V钢热压缩实验结果,绘制出 -
-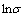 的
的 -
-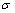 关系图(见图2(a)和图2(b)),并采用最小二乘法进行线性回归,求出各条直线的斜率。式(5)适用于低应力水平,因此,在图2(a)中,取1 273 K和1 373 K时2条直线斜率的倒数平均值求出
关系图(见图2(a)和图2(b)),并采用最小二乘法进行线性回归,求出各条直线的斜率。式(5)适用于低应力水平,因此,在图2(a)中,取1 273 K和1 373 K时2条直线斜率的倒数平均值求出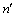 为7.087 7。式(6)适用于高应力水平,因此,在图2(b)中取1 123 K和1 173 K时的2条直线斜率的倒数平均值求出
为7.087 7。式(6)适用于高应力水平,因此,在图2(b)中取1 123 K和1 173 K时的2条直线斜率的倒数平均值求出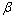 为0.061 6。根据公式
为0.061 6。根据公式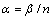 求得
求得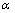 为0.008 7 MPa-1,将求得的
为0.008 7 MPa-1,将求得的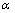 代入式(7),绘制出
代入式(7),绘制出 -
-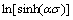 关系图(图2(c)),取直线斜率倒数的平均值求得n为6.008 8。当应变速率一定时,
关系图(图2(c)),取直线斜率倒数的平均值求得n为6.008 8。当应变速率一定时,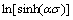 与
与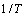 呈线性关系,绘制
呈线性关系,绘制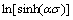 -
- 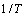 关系图(见图2(d)),求得A为7.458 210 21 s-1,应变激活能为589.871 kJ/mol。
关系图(见图2(d)),求得A为7.458 210 21 s-1,应变激活能为589.871 kJ/mol。
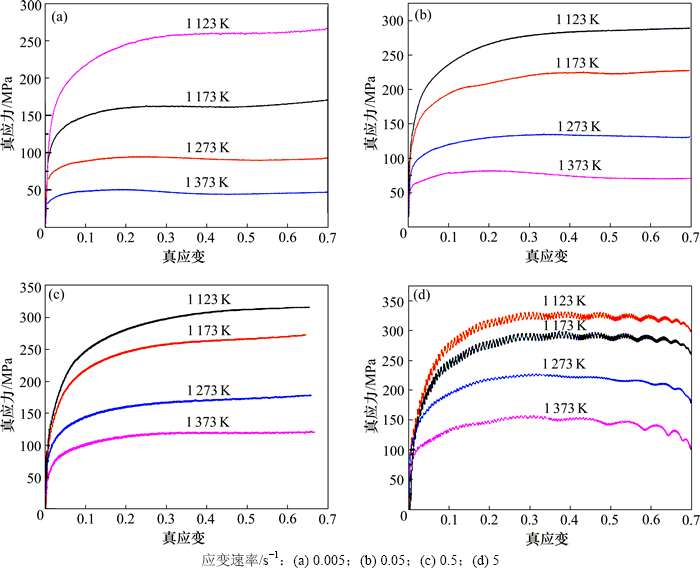
图1 热压缩变形条件的真应力-真应变曲线
Fig. 1 True stress-strain curves of hot compression
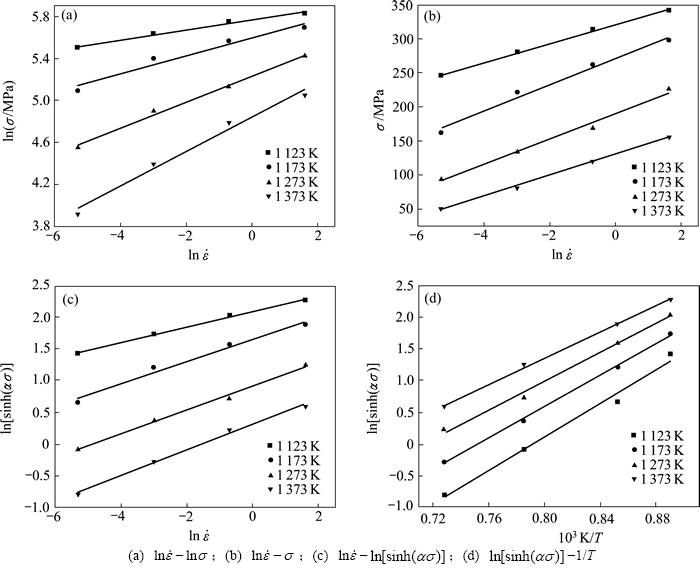
图2 2Cr12NiMo1W1V钢的流变应力与应变速率、变形温度之间的关系
Fig. 2 Relationships among strain rate,flow stress and deformation temperature of 2Cr12NiMo1W1V steel
金属和合金热加工变形时,应变速率受到热激活控制,为了综合描述变形温度和应变速率对合金流变行为的影响,Zener等[11]提出了温度补偿的变形速率因子Z:
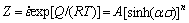 (8)
(8)
对式(8)两边取对数得
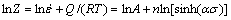 (9)
(9)
根据式(9)可求得对应的 ,进而可作出
,进而可作出 -
-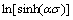 的关系,见图3。经线性回归发现
的关系,见图3。经线性回归发现 与
与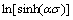 的线性相关系数为0.987,表明2Cr12NiMo1W1V钢热压缩变形时的流变应力与变形温度与应变速率之间可用Arrhenius关系描述。根据双曲正弦函数的定义和式(8)可将流变应力表达成
的线性相关系数为0.987,表明2Cr12NiMo1W1V钢热压缩变形时的流变应力与变形温度与应变速率之间可用Arrhenius关系描述。根据双曲正弦函数的定义和式(8)可将流变应力表达成
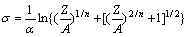 (10)
(10)
将求得的A,n,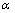 和Q代入式(1),(8)和(10)得2Cr12NiMo1W1V钢的热变形流变应力方程:
和Q代入式(1),(8)和(10)得2Cr12NiMo1W1V钢的热变形流变应力方程:
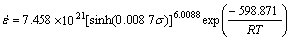 (11)
(11)
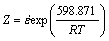 (12)
(12)
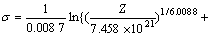
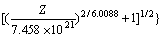 (13)
(13)
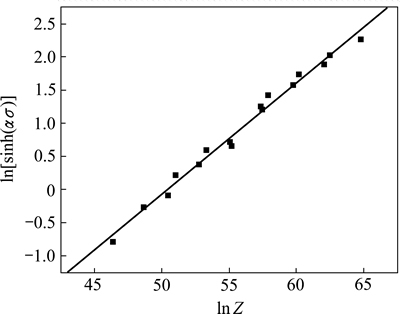
图3 流变应力与参数ln Z之间的关系
Fig. 3 Relationship between flow stress and ln Z
为验证推导的热变形本构模型的精确度,根据式(12)和式(13)计算出不同变形条件下的峰值应力,并与实验结果进行对比,如图4所示。从图4可以看出:峰值应力预测值与实验值很接近,最大相对误差为9.15%,最小相对误差为0.22%,平均相对误差约为5.00%。实验测得的峰值应力与由流变应力本构模型计算的峰值应力非常接近,可为2Cr12NiMo1W1V钢热成形加工工艺的制定提供理论依据。
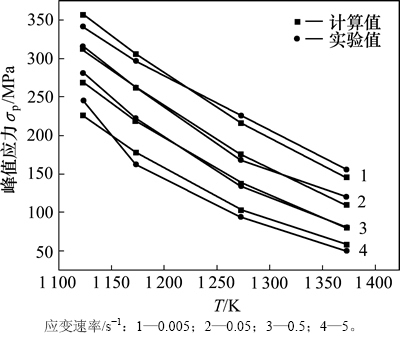
图4 预测峰值应力与实验值对比
Fig. 4 Comparison of predicted peak stress and experimented peak stress
3 热加工图构建及分析
PRASAD等[12]根据大塑性变形连续介质力学、物理模型和不可逆热力学理论,建立了基于动态材料模型(dynamic materials model, DMM)的热加工图,可用于分析材料在不同变形温度和应变速率条件下的高温变形机制,获得塑性加工的“失稳区”和“安全区”,达到控制组织演变、避免缺陷产生和优化工艺参数的目的。
根据动态材料理论,热加工变形是一个能量耗散过程,外界输入的能量P消耗在2方面:一是用于材料的塑性变形,用G表示;二是用于材料显微组织转变,用J表示。总能量P可表示为[13]
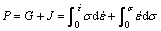 (14)
(14)
在指定温度和应变速率条件下,J和G的变化率可用应变速率敏感性指数m表示:
 (15)
(15)
对于非线性耗散,可用能量耗散因子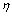 反映材料的能量耗散特征。
反映材料的能量耗散特征。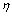 随温度和应变速率的变化构成了能量耗散图,表示材料微观表征组织演变时功率的耗散。
随温度和应变速率的变化构成了能量耗散图,表示材料微观表征组织演变时功率的耗散。
 (16)
(16)
根据不可逆热力学极值原理,可采用量纲一失稳参数 (式(17))来表示塑性变形时的连续失稳判据,
(式(17))来表示塑性变形时的连续失稳判据, 随温度、应变速率的变化就构成了失稳图。当
随温度、应变速率的变化就构成了失稳图。当 <0时,为非稳态流动,变形处于失稳状态。将不同温度、应变速率下的能量耗散图与失稳图进行叠加可得到材料的热加工图[14]。
<0时,为非稳态流动,变形处于失稳状态。将不同温度、应变速率下的能量耗散图与失稳图进行叠加可得到材料的热加工图[14]。
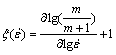 (17)
(17)
将2Cr12NiMo1W1V钢在特定变形量、不同变形条件下的真应力-真应变进行拟合,得到 关于
关于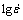 的3次项拟合函数,代入式(15)可求得该变形量下的应变速率敏感性指数m。m的波动反映了塑性变形内部组织转变过程的变化。图5所示为不同应变下,应变速率敏感性指数m随温度、应变速率变化的响应特征曲面。从图5可见:虽然2Cr12NiMo1W1V钢的压缩变形是一个复杂的动态转变过程,但还是可以发现m对温度、应变速率的响应存在一些明显的共性规律;m随着温度的升高、应变速率的降低而增大。这是因为温度越高,非基面滑移的临界应力越低,应变速率越低,非基面滑移时间越长,使得非基面滑移成为主要变形机制,引起微观组织转变耗散热量增加,导致m增加。此外,应变对m也有较大影响。随着压缩应变的增大,在滑移带上会出现另一种变形机制机制即孪生。变形孪晶的大量出现,引起m增加[15]。m反映了塑性变形内部组织转变耗散热量的变化,但确定塑性变形的“失稳区”、“安全区”还需结合能量耗散图和流变失稳图进一步分析。
的3次项拟合函数,代入式(15)可求得该变形量下的应变速率敏感性指数m。m的波动反映了塑性变形内部组织转变过程的变化。图5所示为不同应变下,应变速率敏感性指数m随温度、应变速率变化的响应特征曲面。从图5可见:虽然2Cr12NiMo1W1V钢的压缩变形是一个复杂的动态转变过程,但还是可以发现m对温度、应变速率的响应存在一些明显的共性规律;m随着温度的升高、应变速率的降低而增大。这是因为温度越高,非基面滑移的临界应力越低,应变速率越低,非基面滑移时间越长,使得非基面滑移成为主要变形机制,引起微观组织转变耗散热量增加,导致m增加。此外,应变对m也有较大影响。随着压缩应变的增大,在滑移带上会出现另一种变形机制机制即孪生。变形孪晶的大量出现,引起m增加[15]。m反映了塑性变形内部组织转变耗散热量的变化,但确定塑性变形的“失稳区”、“安全区”还需结合能量耗散图和流变失稳图进一步分析。

图5 不同应变下,应变速率敏感系数m对温度及应变速率的响应曲面
Fig. 5 Response surfaces of strain rate sensitivity m on temperature and strain at different strains
根据拟合的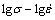 的3次拟合函数,以及式(16)和式(17)计算可分别得能量耗散因子
的3次拟合函数,以及式(16)和式(17)计算可分别得能量耗散因子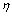 、失稳因子
、失稳因子 ,绘制不同温度和应变速率下的能量耗散图和流变失稳图,并进行叠加,得到热变形加工图。图6所示为应变为0.2,0.3,0.4和0.5时的热加工图,图中等值线的数字表示能量耗散因子
,绘制不同温度和应变速率下的能量耗散图和流变失稳图,并进行叠加,得到热变形加工图。图6所示为应变为0.2,0.3,0.4和0.5时的热加工图,图中等值线的数字表示能量耗散因子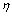 ,阴影区为流变失稳区。比较图6中4个应变量下的加工图可发现:加工图各个区域能量耗散因子
,阴影区为流变失稳区。比较图6中4个应变量下的加工图可发现:加工图各个区域能量耗散因子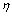 有明显变化;随着变形温度的升高和应变速率的降低,合金的耗散因子
有明显变化;随着变形温度的升高和应变速率的降低,合金的耗散因子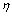 不断增大,而随着应变量的变化,
不断增大,而随着应变量的变化,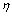 变化幅度不大;当应变较低时,低应变速率失稳区范围较大;随着应变增加,低应变速率失稳区向低温方向收缩,开始出现高温失稳区,并向高应变速率方向迁移;当应变达到0.3时,2Cr12NiMo1W1V钢的热加工图基本保持恒定,“失稳区”和“安全区”不再随应变发生显著变化。这是由于应变达到0.3后,材料热变形进入稳态阶段,这与图1反映的材料流变行为一致。
变化幅度不大;当应变较低时,低应变速率失稳区范围较大;随着应变增加,低应变速率失稳区向低温方向收缩,开始出现高温失稳区,并向高应变速率方向迁移;当应变达到0.3时,2Cr12NiMo1W1V钢的热加工图基本保持恒定,“失稳区”和“安全区”不再随应变发生显著变化。这是由于应变达到0.3后,材料热变形进入稳态阶段,这与图1反映的材料流变行为一致。
以应变为0.5时的热加工图进行分析,结果如图6(d)所示。2Cr12NiMo1W1V钢在该条件下压缩变形时,存在着图中阴影所示的2个流变失稳区。Ⅰ区是温度为1 100~1 270 K、应变速率为0.005~0.3 s-1时的低温低应变速率区域。这是由于在低应变速率下,变形时间较长,合金倾向于发生再结晶,使得在原始晶界出现了大量不均匀弥散分布的新生再结晶晶粒;同时,再结晶是一个热激活过程,当温度较低时,晶内储存能较低,不足以驱使合金发生完全再结晶。因此,晶界在运动过程中受到新生再结晶晶粒的阻碍,导致不均匀变形,从而出现流变失稳。Ⅱ区是温度为1 300~ 1 400 K、应变速率为1~5 s-1时的高温高应变速率区域。一方面,由于温度较高时,合金的晶内激活能较高,晶界和相界容易发生滑动,在晶界和相界面处形成大量位错,造成应力集中,合金发生不连续的动态再结晶;另一方面,由于应变速率较高时,变形时间短,在变形过程中产生的热量难以散出,容易出现绝热剪切效应,形成绝热剪切带,使得该合金在绝热剪切带处出现流变失稳现象。2Cr12NiMo1W1V钢压缩变形达到稳定时的变形安全区可分为2部分:一是低温高应变速率区域Ⅲ,温度为1 200~1 280 K,应变速率为1~5 s-1,由于应变速率较高,合金变形快,合金变形来不及发生再结晶或只有少量的再结晶形核,该区域以动态回复为主;另一区域为高温低应变速率区域Ⅳ,温度为1 320~1 400 K,应变速率为0.1~0.3 s-1,该区域合金的功率耗散因子均大于0.3,最大值可达0.39,一般认为功率耗散因子越大,能量耗散越低,合金的内在加工性能越好[16]。Ⅳ区域温度较高,原子的热振动扩大,原子扩散速率增加,位错运动变得容易,晶界迁移能力提高,而应变速率较低使得合金有充足的时间进行动态再结晶和形核长大,在该区域塑性变形得到均匀细小的再结晶组织,所以,2Cr12NiMo1W1V钢在Ⅲ和Ⅳ区条件下进行塑性变形最适宜。
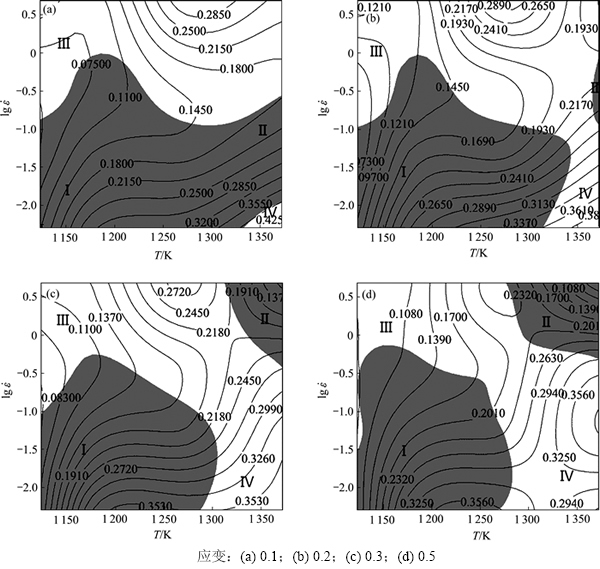
图6 不同应变2Cr12NiMo1W1V钢热加工图
Fig. 6 Hot processing map for 2Cr12NiMo1 W1V steel at different strains
4 结论
1) 2Cr12NiMo1W1V超临界马氏体不锈钢的流变应力在热压缩变形初期,随应变的增加而迅速增大,随后真应力并不随着应变的增大而发生明显的变化,呈现稳态流变特征。温度和应变速率对流变应力影响较大。在变形速率一定时,流变应力随温度的升高而降低;在一定温度下,随着应变速率的增加,流变应力增大,为正应变速率敏感材料。
2) 2Cr12NiMo1W1V超临界马氏体不锈钢稳态应力可用含参数Z修正的双曲正弦模型描述,预测值与实验值拟合程度较高,表明该模型可较好地表征材料的流变行为。流变应力本构方程为
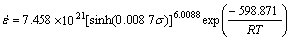
其中,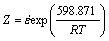 。
。
3) 2Cr12NiMo1W1V超临界马氏体不锈钢变形“失稳区”和“安全区”在稳态流变之前随着应变增大而发生迁移,达到稳态变形后基本保持不变。2Cr12NiMo1W1V钢热变形存在2个最佳工艺参数区间,分别为低温高应变区(温度为1 200~1 280 K,应变速率为1~5 s-1)和高温低应变区(温度为1 320~1 400 K,应变速率为0.1~0.3 s-1)。
参考文献:
[1] MASUYAMA F. History of power plants and progress in heat resistant steels[J]. ISIJ International, 2001, 41: 612-625.
[2] 范华, 杨功显. 超临界与超超临界汽轮机组用材[J]. 东方电气评论, 2005, 19(2): 90-97.
FAN Hua, YANG Gongxian. Materials used for supercritical and ultra supercritical steam turbine unit[J]. Dongfang Electric Review, 2005, 19(2): 90-97.
[3] 燕际军. 本钢超临界、超超临界叶片钢的研发[D]. 沈阳: 东北大学材料与冶金学院, 2009: 1-50.
YAN Jijun. Research and development of supercritical, ultra supercritical steel blade in benxi steel[D]. Shenyang: North Eastern University. College of Material and Metallurgy, 2009: 1-50.
[4] 沈邱农, 陈文辉. 超超临界汽轮机的技术特点[J]. 动力工程, 2002, 22(2): 1659-1663.
SHEN Qiunong, CHEN Wenhui. Technical features of ultra-super critical steam turbine[J]. Power Engineering, 2002, 22(2): 1659-1663.
[5] LU Zhiqiang, JU Fengming. Research on material for ultra-super critical steam turbine unit[J]. Challenges of Power Engineering and Environment, 2007, 5: 270-274.
[6] 罗通伟, 陈晋阳. 12%Cr型叶片钢热轧大型材生产工艺初探[J]. 特钢技术, 2004, 9(2): 1-9.
LUO Tongwei, CHEN Jinyang. A study on production of hot rolled 12%Cr turbine bar[J]. Special Steel Technology, 2004, 9(2): 1-9.
[7] DEGUCHI S, OGAWA M, et al. Development of super-and sub-critical water annealing processes[J]. Power Technology, 2013, 249: 163-167.
[8] 奚晓峰. 2Cr12NiMo1W1V异型锻件退火工艺改进[J]. 特钢技术, 2010, 16(3): 15-17.
XI Xiaofeng. Improvement on annealing processing of 2Cr12NiMo1W1Vspecial shaped forging[J]. Special Steel Technology, 2010, 16(3): 15-17.
[9] SELLARS C M, MCTEGART W J. On the mechanism of hot deformation[J]. Acta Metallurgica, 1966, 14(9): 1136-1138.
[10] URCOLA J J, SELLARS C M. A model for mechanical equation of state under continuously changing conditions of deformation[J]. Acta Metallurgica, 1987, 35(11): 2659-2669.
[11] ZENER C, HOLLOMON H. Effect of strain-rate upon plastic flow of steel[J]. Journal of Applied Physical, 1944, 15(1): 22-27.
[12] PRASAD Y V R T, GEGAL H L, DORAIVELU S M, et al. Modeling of dynamic material behavior in hot deformation: Forging of Ti-6264[J]. Metallurgical and Materials Transactions A, 1984, 15(10): 1883-1892.
[13] PADMAVARDHANI D, PRASAD Y V R T. Effect of zinc content on the processing map for hot working of brass[J]. Materials Science and Engineering A, 1992, 157(1): 43-51.
[14] WANG Zhenhua, FU Wangtang, et al. Study on deformation characteristics of 12%Cr ultra-super-critical rotor steel using processing maps and Zener-hollomon parameter[J]. Materials Characterization, 2010, 61(1): 25-30.
[15] JORGE A, AMBROSIO J A C. Material strain rate sensitivity[M]. Crashworthiness, Vienna: Springer, 2001: 33-47.
[16] 韦莉莉, 潘清林, 周坚, 等. Al-Zn-Mg-Cu-Zr合金加工图的构建及失稳分析[J]. 中南大学学报(自然科学版), 2013, 44(5): 1798-1804.
WEI Lili, PAN Qinglin, ZHOU Jian, et al. Processing maps and flow instability analysis of Al-Zn-Mg-Cu-Zr alloy[J]. Journal of Central South University (Science and Technology), 2013, 44(5): 1798-1804.
(编辑 陈灿华)
收稿日期:2015-01-10;修回日期:2015-03-20
基金项目(Foundation item):科技部重大专项(2012ZX04010-081) (Project(2012ZX04010-081) supported by the Major Project of the Ministry of Science and Technology)
通信作者:王梦寒,博士(后),副教授,硕士生导师,从事金属塑性成形工艺及模具CAD/CAE/CAM技术研究;E-mail: wmh9792@163.com