DOI: 10.11817/j.issn.1672-7207.2020.03.005
工程机械用Q1100钢的热变形应变补偿本构方程
李红英1,赵菲1,刘丹2,张青学2,倪川皓3
(1. 中南大学 材料科学与工程学院, 湖南 长沙, 410083;
2. 湖南华菱湘潭钢铁有限公司, 湖南 湘潭, 411101;
3. 中联重科股份有限公司, 湖南 长沙, 410013)
摘要:采用Gleeble-3800热模拟试验机研究工程机械用Q1100钢在变形温度为850~1 200 ℃、应变速率为0.01~10.00 s-1条件下的热变形行为,建立恒定应变与应变补偿的Arrhenius本构方程。研究结果表明:随着变形温度升高、应变速率减小,Q1100钢的流变应力降低,真应力-真应变曲线发生由动态回复型到动态再结晶型的转变;随应变增加,参数α和n先减小后趋于平缓,Q和lnA先减小后增大,其六次多项式拟合效果较好,相关系数R均在0.98以上;流变应力预测值与实验值的相关系数为0.992 66,绝对误差在15 MPa内的数据点有92.13%,平均相对误差为5.25%,验证了模型的准确性。
关键词:工程机械用Q1100钢;热压缩变形;本构方程;误差分析
中图分类号:TG142.1 文献标志码:A
文章编号:1672-7207(2020)03-0608-11
Thermal deformation strain compensation constitutive equation for Q1100 steel for construction machinery
LI Hongying1, ZHAO Fei1, LIU Dan2, ZHANG Qingxue2, NI Chuanhao3
(1. School of Materials Science and Engineering, Central South University, Changsha 410083, China;
2. Xiangtan Iron & Steel Co., Ltd of Hunan Valin, Xiangtan 411101, China;
3. Zoomlion Heavy Industry Science & Technology Co., Ltd., Changsha 410013, China)
Abstract: The hot deformation behavior of Q1100 steel for construction machinery at deformation temperature of 850-1 200 ℃ and strain rate of 0.01-10.00 s-1 was studied by Gleeble-3800 thermal simulator. Arrhenius constitutive equation of constant strain and strain compensation was established. The results show that the flow stress of Q1100 steel decreases with the increase of deformation temperature and the decrease of strain rate, and the flow stress curve changes from dynamic recovery to dynamic recrystallization. The parameters α and n decrease first with the increase of strain and then tend to be gentle. Q and lnA decrease firstly and then increase with the increase of strain, and the sixth-order polynomial fitting effect is good, and the correlation coefficient R is above 0.98. The error analysis shows that the correlation coefficient between the predicted value of the strain stress and the experimental value is 0.992 66, the data point with absolute error within 15 MPa is 92.13%, and the average relative error is 5.25%, which verifies the accuracy of the model.
Key words: Q1100 steel for construction machinery; hot compression deformation; constitutive equation; error analysis
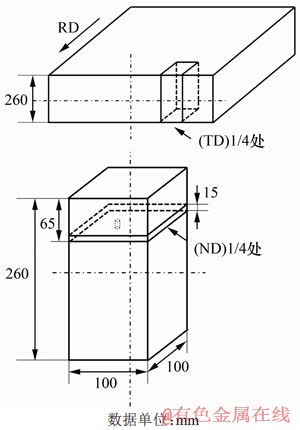
图1 铸坯取样示意图
Fig. 1 Schematic diagram of slab sampling
随着工程机械不断向大型化、轻量化方向发展,对高强、高品质工程机械用钢的需求量持续增长。目前,国内工程机械用屈服强度690 MPa及以下级别高强钢以国产为主[1],而屈服强度960 MPa及以上级别钢主要依靠进口[2-3],国产该级别钢在产品质量、规格和供给能力方面都存在突出问题[4],严重制约了国内工程机械行业的发展。为实现技术突破,国内对屈服强度960 MPa以上级别的钢进行了较广泛的研究,但主要集中在热处理和焊接方面[5-10],关于热变形的研究较少,且多围绕探索控轧控冷工艺。孙浩源等[11]通过实验室模拟轧制,发现1 080 ℃开轧+940~900 ℃精轧两阶段控轧及直接淬火+250 ℃/1.5 h低温回火后的钢板具有最佳的强韧性配比;段争涛等[12]研究表明:与常规热机械控制工艺(TMCP)相比,采用高温轧制+超快冷工艺生产的8 mm厚钢板,组织明显细小,力学性能优异,轧机负荷较低;陈晓潇等[13]研究了2种成分、4种轧制工艺对低合金高强钢组织性能的影响,最终获得具有良好塑性和焊接性的低成本结构钢。常规的实验方法虽然能够直接得到实验钢的工艺-组织-性能对应关系,但由于实验工作量较大,可探索工艺数量及范围十分有限。通过热模拟实验研究Q1100钢的热变形行为,可减少实验用料及工作量,扩大工艺研究范围,且可获取流变应力与变形工艺之间的定量关系,实现对工业生产的精确指导。很多学者对钢铁的热变形行为进行了研究,如CHEN等[14]建立了超临界转子钢在900~1 200 ℃,0.001~0.100 s-1范围内峰值条件下的流变应力本构方程;陈学文等[15]考虑了应变对15CrMoR钢流变行为的影响,建立了800~1 150 ℃,0.002~5.000 s-1范围内应变补偿的热变形本构方程,并取得了较好的预测结果,但是,目前对Q1100钢的本构方程的研究较少。本文作者以国内自主生产的Q1100钢锭为原料,通过热压缩模拟实验,研究Q1100钢在不同变形温度、应变速率下的热变形行为,建立了恒定应变及应变补偿的本构方程,并分析预测值与测试值的误差,验证模型准确性。
1 实验
实验材料为工厂生产的Q1100铸坯钢,其化学成分如表1所示。
表1 实验Q1100钢的化学成分(质量分数)
Table 1 Chemical composition of experimental Q1100 steel %

在厚度为260 mm的铸钢坯上沿横向(TD)和法向(ND)1/4处取样(如图1所示)。利用线切割加工成直径×长度为10 mm×15 mm的试样,采用Gleeble-3800热模拟实验机进行恒温、恒应变速率的单道次热压缩实验。实验前,在试样两端贴上带有高温润滑剂的云母片以减小摩擦对变形的影响,在试样中间焊上2根热电偶丝实时记录实验温度的变化,通过设备夹头固定试样,设置计算机控制系统的实验参数,完成整个压缩过程。
图2所示为热压缩试验的工艺示意图,试验先以10 ℃/s的速度升温至1 200 ℃,保温180 s完成奥氏体化,再以10 ℃/s的速度降温至变形温度,等温60 s后进行单向热压缩,变形完成后立即水淬。参考工厂热轧工艺参数取值范围,制定变形工艺如下:变形温度为850,900,950,1 000,1 050, 1 100,1 150,1 200 ℃,应变速率为0.01,0.10,1.00,5.00和10.00 s-1,变形量为65%。
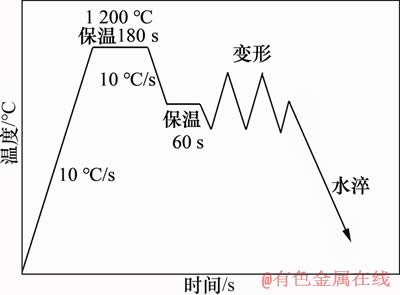
图2 Q1100钢的热变形工艺
Fig. 2 Hot deformation process of Q1100 steel
2 结果与讨论
2.1 真应力-真应变曲线
通过不同变形温度和应变速率的热压缩实验,得到Q1100钢的真应力-真应变曲线,如图3所示。从图3可以看出:在相同应变速率下,流变应力随变形温度升高而降低,在相同变形温度下,流变应力随应变速率升高而升高,说明Q1100钢具有负温度敏感性及正应变速率敏感性。温度升高会提高金属原子的扩散速度,促进热激活,使加工硬化增殖的位错加快发生交滑移或攀移,部分位错消失或重新排列,动态软化作用增加,流变应力降低。应变速率增大,材料变形时间大幅缩短,位错增殖速率增加,材料在短时间内来不及通过位错的交滑移或攀移进行充分的动态软化,流变应力增加[16]。
当应变速率为1.00 s-1时,变形温度低于1 100 ℃的流变应力曲线呈动态回复型,随着应变增加,应力达到峰值后趋于平缓或持续上升,这是由于较低温度下动态回复引起的软化作用较小,不能完全抵消加工硬化引起的应力上升;而变形温度1 100 ℃及以上的流变应力曲线呈动态再结晶型,随着应变增加,应力达到峰值后先下降后趋于平缓,这是由于较高温度下动态再结晶的软化作用会强于加工硬化[17]。当变形温度为1 050 ℃时,应变速率高于0.10 s-1的流变应力曲线呈动态回复型,应变增加,应力达到峰值后进入稳态流变阶段;而应变速率为0.10 s-1及以下的流变应力曲线呈动态再结晶型。
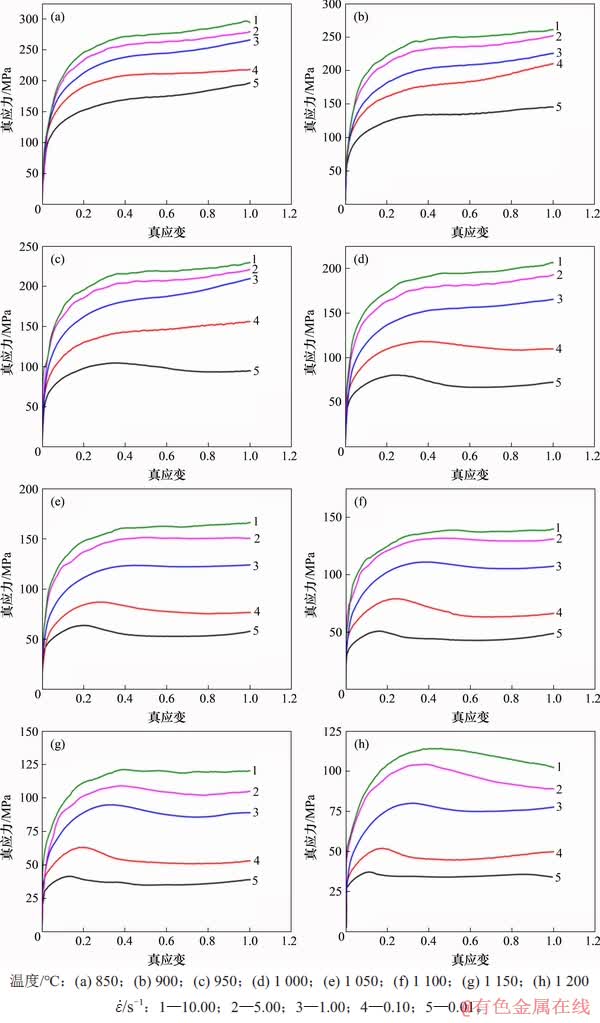
图3 Q1100钢的真应力-真应变曲线
Fig. 3 True stress-true strain curves of Q1100 steel
综上可知,随着变形温度升高、应变速率降低,流变应力曲线出现从动态回复型到动态再结晶型的转变,这是由于较高的变形温度与较低的应变速率为材料提供了足够的能量和时间发生再结晶[18]。
2.2 恒定应变下的本构方程
流变应力是热变形过程中的重要参量,流变应力、变形温度和应变速率之间的关系可用Sellars和Tegart提出的双曲正弦修正的Arrhenius方程[19-21]表示:
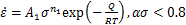 (1)
(1)
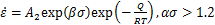 (2)
(2)
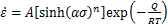 ,所有
,所有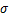 (3)
(3)
式中:A1,A2,A,n1,β,α,n均为与材料有关的常数,且α=β/n1;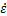 为应变速率,s-1;
为应变速率,s-1;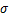 为流变应力,MPa;R为气体常数,R=8.314 J/(mol·K);T为变形温度,K;Q为热变形激活能,J/mol。
为流变应力,MPa;R为气体常数,R=8.314 J/(mol·K);T为变形温度,K;Q为热变形激活能,J/mol。
通常使用幂函数方程(1)描述低应力水平的热变形流变应力行为,使用指数函数方程(2)描述高应力水平的热变形流变应力行为,使用双曲正弦函数方程(3)描述不同应力水平的变形过程。
变形温度与应变速率的关系用温度补偿的应变速率因子Z参数[22-24]表示:
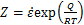 (4)
(4)
将式(4)代入式(3),则流变应力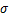 可表达为Z的函数:
可表达为Z的函数:
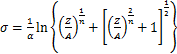 (5)
(5)
对式(1)~(3)两边分别取对数可得:
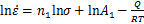 (6)
(6)
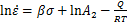 (7)
(7)
 (8)
(8)
可见:Arrhenius本构方程未涉及到应变,而流变应力与应变有关,利用不同应变下的流变应力计算得到的Arrhenius本构方程将有所不同。以恒定应变0.3为例,将对应流变应力代入式(6)~(8)中,对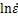 -
-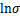 ,
,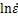 -
-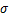 散点进行线性拟合,结果如图4(a)和(b)所示,求得n1=8.673 67,β=0.072 85,则α=β /n1=0.008 40,对
散点进行线性拟合,结果如图4(a)和(b)所示,求得n1=8.673 67,β=0.072 85,则α=β /n1=0.008 40,对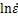 -
-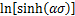 散点进行线性拟合,结果如图4(c)所示,求得n=6.139 48。
散点进行线性拟合,结果如图4(c)所示,求得n=6.139 48。
对方程(8)进行变换可得:
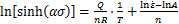 (9)
(9)
同样选取应变为0.3时的流变应力计算Q1100钢的热变形激活能Q与材料常数lnA。将不同变形温度、应变速率的流变应力代入式(8),通过对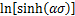 -
-  散点进行线性拟合,结果如图4(d)所示,求得Q=404.125 83 kJ/mol,lnA=35.571 88。研究[25-26]表明:相近成分钢的热变形激活能分别为395.18 kJ/mol和411.92 kJ/mol,可见:计算得到的Q1100钢热变形激活能与文献报道相差不大,大于Fe在γ-Fe中的自扩散激活能270 kJ/mol[27]。
散点进行线性拟合,结果如图4(d)所示,求得Q=404.125 83 kJ/mol,lnA=35.571 88。研究[25-26]表明:相近成分钢的热变形激活能分别为395.18 kJ/mol和411.92 kJ/mol,可见:计算得到的Q1100钢热变形激活能与文献报道相差不大,大于Fe在γ-Fe中的自扩散激活能270 kJ/mol[27]。
将计算得到的 ,n,Q,A代入式(3),得到应变为0.3时的热变形本构方程:
,n,Q,A代入式(3),得到应变为0.3时的热变形本构方程:
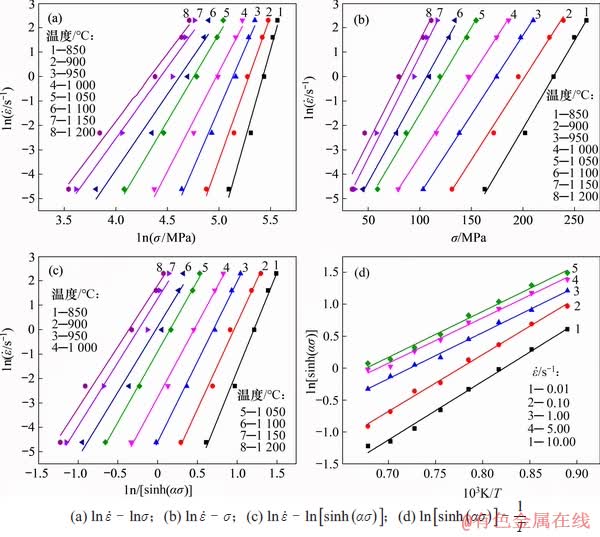
图4 恒定应变0.3时不同变量之间的拟合曲线
Fig. 4 Fitting curves between different variables at constant strain of 0.3
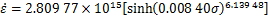
 (10)
(10)
将计算得到的Q代入式(4)可得:
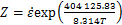 (11)
(11)
将各参数代入式(5),则应变为0.3时Q1100钢应力方程可以用Z函数表示为
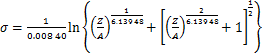 (12)
(12)
2.3 考虑应变补偿的本构方程
恒定应变下,Arrhenius本构方程反映流变应力与变形条件之间的关系,未考虑热变形过程中应变对流变应力的影响,无法预测Q1100钢在不同应变下的流变应力,因此需对其进行应变补偿[28-29]。采用上述计算方法分别求出应变为0.05~1.00范围内共20个条件下的材料常数α,n,lnA和热变形激活能Q,计算结果如表2所示。从表2可以看出:应变对材料常数α,n,lnA及热变形激活能Q的影响很大,α和n随应变的增加先减小后趋于稳定,lnA和Q随应变的增加先减小后增大。为更精确地描述这些参数与应变之间的关系,利用表2中的数据绘制α-ε,n-ε,Q-ε及lnA-ε散点图并进行六次多项式拟合,拟合结果如图5所示,得到α(ε),n(ε),Q(ε)和lnA(ε)的函数表达式:
表2 不同应变下的Arrhenius本构方程参数
Table 2 Arrhenius constitutive equation parameters under different strains
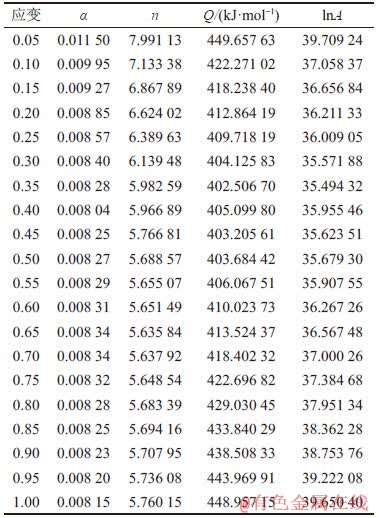
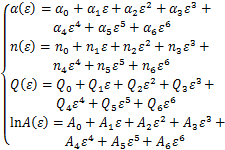 (13)
(13)

图5 材料常数α,n,Q,lnA与应变ε的拟合曲线
Fig. 5 Fitting curves of material parameters α, n, Q, lnA and strain ε
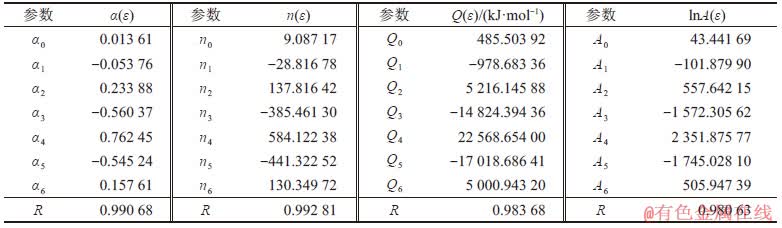
表3所示为拟合曲线函数表达式的各项系数及拟合结果的线性相关系数R。从表3可以看出:各参数拟合的相关系数R均在0.98以上,表明六次多项式的拟合效果较好。
将式(13)代入式(3),并结合表3的六次多项式系数,可得到Q1100钢在变形温度为850~1 200 ℃,应变速率为0.01~10.00 s-1的变形条件下考虑应变补偿的Arrhenius本构方程:
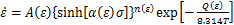 (14)
(14)
将计算得到的Q(ε)表达式代入式(4)可得:
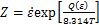 (15)
(15)
将各参数表达式代入式(5),则Q1100钢考虑应变补偿的应力方程可用Z函数表示:
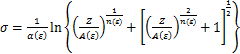 (16)
(16)
表3 各材料常数的多项式拟合系数及线性相关系数R
Table 3 Polynomial fitting coefficient and correlation coefficient R of each material parameters
2.4 本构方程的验证及误差分析
采用建立的Arrhenius本构方程预测实验条件下不同应变对应的流变应力,并与实验值进行对比,结果如图6所示。
由图6可知:本构方程预测的流变应力趋势与实验值基本保持一致,说明建立的本构方程对预测Q1100钢在变形温度为850~1 200 ℃,应变速率为0.01~10.00 s-1的变形条件下的流变应力具有一定的可靠性。但是,由图6(h)可以看出:当变形温度为1 200 ℃时,应变速率为5.00 s-1和10.00 s-1的流变应力预测误差较大,可能是由于求解本构方程参数Q时未考虑应变速率对Q的影响,但实际上,应变速率越高,材料越难变形,其热变形激活能越大,以平均值Q代入计算会使计算值偏低。
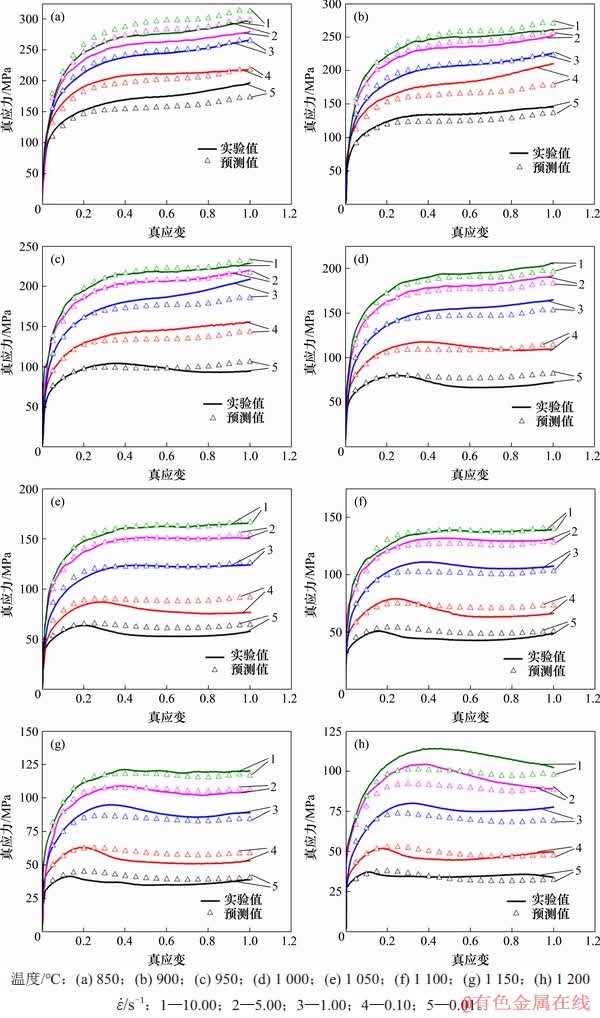
图6 Arrhenius本构方程预测值与实验值对比
Fig. 6 Comparison of predicted values of Arrhenius constitutive equation and experimental values
为进一步描述上述本构方程的精确度,对方程预测值与实验值进行误差分析[30],采用相关系数R分析预测值与实验值之间的线性强弱,计算表达式如式(17)所示。
 (17)
(17)
式中: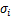 为实验值;
为实验值;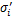 为预测值;
为预测值; 和
和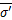 分别为
分别为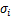 和
和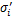 的平均值;N为数据个数。
的平均值;N为数据个数。
绝对误差Ea可以反映预测值与实验值之间的偏差水平:
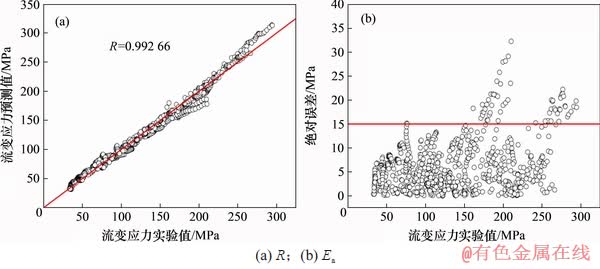
图7 Arrhenius本构方程预测值与实验值的误差计算
Fig. 7 Error calculation of predicted values of Arrhenius constitutive equation and experimental values
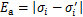 (18)
(18)
采用平均相对误差EAR逐项计算预测值与实验值整体的相对误差,计算表达式如式(19)所示。
 (19)
(19)
以实验条件下不同应变对应的流变应力预测值与实验值为数据样本,进行误差计算,计算结果如图7与表4所示。
表4 Arrhenius本构方程预测值与实验值的平均相对误差
Table 4 Average relative error between predicted values of Arrhenius constitutive equation and experimental values%
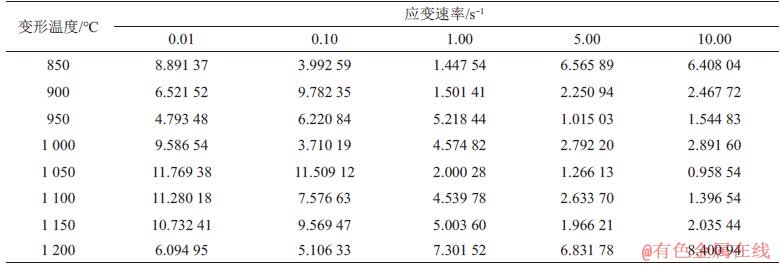
从图7可以看出:利用上述方程预测的流变应力与实验值相差不大,绝对误差在0~15 MPa范围的数据点约占92.13%;从表4可以看出,90%平均相对误差都小于10%,计算得到所有数据的平均相对误差为5.25%,说明采用应变补偿的Arrhenius本构模型预测Q1100钢的流变应力具有较高的准确性。
3 结论
1) 变形温度升高、应变速率减小,Q1100钢的流变应力降低,真应力-真应变曲线出现从动态回复型到动态再结晶型的转变。
2) 当应变为0.3时,Q1100钢的热变形激活能为404.125 83 kJ/mol,其Arrhenius本构方程为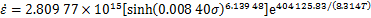 。
。
3) Q1100钢的Arrhenius本构方程参数α,N,Q,lnA与应变ε有关,α和n随应变的增加先减小后趋于平缓,Q和lnA随应变的增加先减小后增大,其六次多项式拟合效果较好,相关系数R均在0.98以上。
4) 应变补偿Arrhenius本构方程具有较高准确性,流变应力预测值与实验值的相关系数R为0.992 66;绝对误差大多在15 MPa以内,占比92.13%;平均相对误差为5.25%,误差较小,可为实际生产提供参考。
参考文献:
[1] SHI Gang, ZHU Xi, BAN Huiyong. Material properties and partial factors for resistance of high-strength steels in China[J]. Journal of Constructional Steel Research, 2016, 121: 65-79.
[2] 陈付红, 丁伟, 黄维, 等. 国外先进公司工程机械用高强钢发展现状[J]. 上海金属, 2015, 37(1): 47-51.
CHEN Fuhong, DING Wei, HUANG Wei, et al. Development status of foreign high strength steel for engineering machinery[J]. Shanghai Metals, 2015, 37(1): 47-51.
[3] AFKHAMI S, BJORK T, LARKIOLA J. Weldability of cold-formed high strength and ultra-high strength steels[J]. Journal of Constructional Steel Research, 2019, 158: 86–98.
[4] 郑瑞, 李飞. 高强度工程机械用钢板应用现状和发展前景[J]. 冶金信息导刊, 2010, 47(2): 34-38.
ZHENG Rui, LI Fei. Application status and prospect of high strength steel plates for construction machine[J]. Metallurgical Information Review, 2010, 47(2): 34-38.
[5] YUN Yang, CAI Qingwu, XIE Baosheng, et al. Effect of tempering temperature on strain hardening exponent and flow stress curve of 1000 MPa grade steel for construction machinery[J]. Journal of Iron and Steel Research International, 2017, 24(9): 950-956.
[6] 张宠元. 回火对Q960高强钢析出物和应变硬化行为的影响[J]. 金属热处理, 2018, 43(12): 186-191.
ZHANG Chongyuan. Effect of tempering on precipitates and strain hardening behavior of Q960 steel[J]. Heat Treatment of Metals, 2018, 43(12): 186-191.
[7] 闫强军, 温长飞, 姜在伟, 等. 淬火工艺对Q1100超高强度工程机械用钢组织与性能的影响[J]. 上海金属, 2018, 40(6): 39-44.
YAN Qiangjun, WEN Changfei, JIANG Zaiwei, et al. Effect of quenching process on microstructure and properties of Q1100 ultra-high strength engineering machinery steel[J]. Shanghai Metals, 2018, 40(6): 39-44.
[8] 温长飞, 邓想涛, 王昭东, 等. 超高强钢Q1100的SH-CCT曲线及粗晶热影响区组织和性能[J]. 东北大学学报(自然科学版), 2017, 38(6): 809-813.
WEN Changfei, DENG Xiangtao, WANG Zhaodong, et al. SH-CCT diagram, microstructure and properties of coarse grain heat-affected zone in Q1100 ultra-high strength steel[J]. Journal of Northeastern University(Natural Science), 2017, 38(6): 809-813.
[9] TONG Lewei, NIU Lichao, JING Shuang, et al. Low temperature impact toughness of high strength structural steel[J]. Thin-Walled Structures, 2018, 132: 410-420.
[10] 王青春, 张文金, 陈佳, 等. 基于焊接热模拟的工程机械用高强钢热影响区组织和力学性能研究[J]. 热加工工艺, 2017, 46(3): 204-207.
WANG Qingchun, ZHANG Wenjin, CHEN Jia, et al. Study on microstructure and mechanical properties of HAZ of high strength steel for engineering machinery based on welding thermal simulation[J]. Hot Working Technology, 2017, 46(3): 204-207.
[11] 孙浩源, 唐广波, 李胜利, 等. 控轧控冷工艺对低合金超高强度工程机械用钢组织和性能的影响[J]. 热加工工艺, 2013, 42(13): 27-30.
SUN Haoyuan, TANG Guangbo, LI Shengli, et al. Effect of controlled rolling and controlled cooling processes on microstructure and properties of low alloyed ultra-high strength steel for engineering machinery[J]. Hot Working Technology, 2013, 42(13): 27-30.
[12] 段争涛, 裴新华, 卞皓. 高温轧制+超快冷工艺在工程机械用钢生产中的应用[J]. 热加工工艺, 2015, 44(5): 163-165.
DUAN Zhengtao, PEI Xinhua, BIAN Hao. Application of high temperature rolling and ultra fast cooling process in engineering machinery steel[J]. Hot Working Technology, 2015, 44(5): 163-165.
[13] 陈晓潇, 唐广波, 李激光, 等. 低合金高强钢试制及轧制工艺对组织和性能的影响研究[J]. 热加工工艺, 2013, 42(9): 30-34.
CHEN Xiaoxiao, TANG Guangbo, LI Jiguang, et al. Trial-production of high strength low alloy steel and effect of rolling process on microstructure and mechanical properties[J]. Hot Working Technology, 2013, 42(9): 30-34.
[14] CHEN Fei, WANG He, ZHU Huajia, et al. High-temperature deformation mechanisms and physical-based constitutive modeling of ultra-supercritical rotor steel[J]. Journal of Manufacturing Processes, 2019, 38: 223-234.
[15] 陈学文, 陈天安, 朱美玲, 等. 45Cr4NiMoV合金钢热变形的本构模型[J]. 金属热处理, 2015, 40(2): 152-155.
CHEN Xuewen, CHEN Tian'an, ZHU Meiling, et al. Constitutive model of 45Cr4NiMoV steel for hot forming process[J]. Heat Treatment of Metals, 2015, 40(2): 152-155.
[16] 蔺永诚, 陈明松, 钟掘. 42CrMo钢的热压缩流变应力行为[J]. 中南大学学报(自然科学版), 2008, 39(3): 549-553.
LIN Yongcheng, CHEN Mingsong, ZHONG Jue. Flow stress behaviors of 42CrMo steel during hot compression[J]. Journal of Central South University(Science and Technology), 2008, 39(3): 549-553.
[17] LIN Yongcheng, LUO Shuncun, JIANG Xingyou, et al. Hot deformation behavior of a Sr-modified Al-Si-Mg alloy: Constitutive model and processing maps[J]. Transactions of Nonferrous Metals Society of China, 2018, 28(4): 592-603.
[18] 蔺永诚, 陈明松, 钟掘. 42CrMo钢形变奥氏体的静态再结晶[J]. 中南大学学报(自然科学版), 2009, 40(2): 411-416.
LIN Yongcheng, CHEN Mingsong, ZHONG Jue. Static recrystallization behaviors of deformed 42CrMo steel[J]. Journal of Central South University(Science and Technology), 2009, 40(2): 411-416.
[19] LI Hongying, WEI Dongdong, HU Jidong, et al. Constitutive modeling for hot deformation behavior of T24 ferritic steel[J]. Computational Materials Science, 2012, 53(1): 425-430.
[20] 易幼平, 杨积慧, 蔺永诚. 7050铝合金热压缩变形的流变应力本构方程[J]. 材料工程, 2007, 35(4): 20-22, 26.
YI Youping, YANG Jihui, LIN Yongcheng. Flow stress constitutive equation of 7050 aluminum alloy during hot compression[J]. Journal of Materials Engineering, 2007, 35(4): 20-22, 26.
[21] 文智, 易丹青, 王斌, 等. Al-6Mg-0.4Mn-0.2Sc铝合金的高温变形行为及热加工图[J]. 中南大学学报(自然科学版), 2013, 44(3): 914-920.
WEN Zhi, YI Danqing, WANG Bin, et al. Hot deformation and processing maps of Al-6Mg-0.4Mn-0.2Sc aluminum alloy[J]. Journal of Central South University(Science and Technology), 2013, 44(3): 914-920.
[22] ZENER C, HOLLOMON J H. Effect of strain rate upon plastic flow of steel[J]. Journal of Applied Physics, 1944, 15(1): 22-32.
[23] MEDINA S F, HERNANDEZ C A. General expression of the Zener-Hollomon parameter as a function of the chemical composition of low alloy and microalloyed steels[J]. Acta Materialia, 1996, 44(1): 137-148.
[24] 覃银江, 潘清林, 何运斌, 等. ZK60镁合金高温流变本构模型[J]. 中南大学学报(自然科学版), 2010, 41(5): 1774-1781.
QIN Yinjiang, PAN Qinglin, HE Yunbin, et al. Constitutive modeling for elevated temperature flow behavior of ZK60 magnesium alloy[J]. Journal of Central South University(Science and Technology), 2010, 41(5): 1774-1781.
[25] 任书杰, 罗飞, 田野, 等. A100超高强度钢的流变应力曲线修正与唯象本构关系[J]. 材料工程, 2019, 47(6): 144-151.
REN Shujie, LUO Fei, TIAN Ye, et al. Flow stress curve correction and phenomenological constitutive relationship of A100 ultra-high strength steel[J]. Journal of Materials Engineering, 2019, 47(6): 144-151.
[26] 章晓婷, 黄亮, 李建军, 等. 300 M高强钢高温流变行为及本构方程[J]. 中南大学学报(自然科学版), 2017, 48(6): 1439-1447.
ZHANG Xiaoting, HUANG Liang, LI Jianjun, et al. Flow behaviors and constitutive model of 300M high strength steel at elevated temperature[J]. Journal of Central South University(Science and Technology), 2017, 48(6): 1439-1447.
[27] 郑子樵. 材料科学基础[M]. 2版. 长沙: 中南大学出版社, 2013: 314-315.
ZHENG Ziqiao. Fundamental of materials science[M]. 2nd ed. Changsha: Central South University Press, 2013: 314-315.
[28] REZAEI ASHTIANI H R, PARSA M H, BISADI H. Constitutive equations for elevated temperature flow behavior of commercial purity aluminum[J]. Materials Science and Engineering: A, 2012, 545: 61-67.
[29] ZHANG Ming, LIU Guoquan, WANG Hao, et al. Modeling of thermal deformation behavior near γ' solvus in a Ni-based powder metallurgy superalloy[J]. Computational Materials Science, 2019, 156: 241-245.
[30] 戴青松, 刘栩, 付平, 等. 5083铝合金高温变形行为及加工图[J]. 中南大学学报(自然科学版), 2017, 48(8): 1988-1994.
DAI Qingsong, LIU Xu, FU Ping, et al. High-temperature deformation behavior and processing map of 5083 aluminum alloy[J]. Journal of Central South University(Science and Technology), 2017, 48(8): 1988-1994.
(编辑 赵俊)
收稿日期: 2019 -07 -26; 修回日期: 2019 -10 -10
基金项目(Foundation item):湖南省省级科技计划项目(2018XK2301) (Project(2018XK2301) supported by the Science and Technology Program of Hunan Province)
通信作者:李红英,教授,从事钢铁材料研究;E-mail: lhying@csu. edu. cn