DOI: 10.11817/j.ysxb.1004.0609.2020-35737
尾砂胶结充填料浆剪切触变实验及其基于量纲分析的触变性预测模型
张友志1,甘德清1,陈 勋2,薛振林1,任伟成1
(1. 华北理工大学 矿业工程学院,唐山 063210;
2. 北京科技大学 土木与资源工程学院,北京 100083)
摘 要:采用桨式流变仪研究了不同质量浓度、灰砂比充填料浆在剪切条件下的触变行为,借助量纲齐次性原理,推导并提出了基于量纲分析的触变性预测模型。结果表明:浓度不同的料浆在触变形态上有差异,高浓度料浆剪切应力的波动性更强;触变性与质量浓度和灰砂比均呈非线性正相关,且水泥比尾砂更能引发触变;剪切过程中,表观黏度先急速下降,然后维持平稳,最后急剧上升,但结束瞬间的最终值小于初始值;质量浓度为64%的料浆剪切应力在剪切速率转折点前呈不规则“U”字型,其他组剪切应力基本以剪切速率转折点为中心左右对称。设计实验对预测模型进行验证,结果显示平均误差率为6.2%,且适应性良好。
关键词:充填料浆;剪切;触变行为;量纲;预测模型
文章编号:1004-0609(2020)-04-0951-09 中图分类号:TD853 文献标志码:A
充填料浆是由尾砂、水泥等固体颗粒与水组成的分散体系[1-3]。流动会引起分散体系可逆和不可逆的结构变化,从流变学的角度表现为表观黏度跟随流动做适应性变化,如果这些变化是可逆的且时间依赖的,那么这种效应被称为触变性[4]。当前,采用桨式流变仪来测量浆体的触变性是最为常见的手段[5],它包括连续地两个阶段:上行阶段,剪切速率由0增加至峰值;下行阶段,剪切速率由峰值降低至0。将瞬态数据绘制成剪切应力与剪切速率的关系时,由于剪切应力落后于剪切速率,因此,瞬态数据关系图中将表现出触变环[6]。触变环的面积被认为是触变性的相对定量表征,已经被广大学者所认可[7]。
根据材料、测试条件的不同,触变环的形态可能会有差异,比如样品的物理化学性质、剪切历史、实验中的最大剪切速率等[8]。图1所示为3种触变环常见的形态:一般地,高均质性浆体在剪切速率均匀增加的条件下,触变环的形态常接近于图1(a)中的形状;图1(b)的情况代表剪切启动后,初始结构的破坏主导了应力在时间上的演变,导致应力在初期产生超调的现象;当在相对较低的剪切速率下引起结构的形成与破坏时,触变环可能会表现为图1(c)中的形状。除此3种之外,触变环的形状也会因测试对象材料的种类与性质呈现其他形态。
由流动引起的微观结构与流变特性的变化相当复杂,至今仍然没有被完全理解,因此,学者对触变性所做的解释与研究也是从各个角度出发的。QIAN等[9]从流变性能的角度展开研究,认为触变性的存在是浆体的动态屈服应力与静态屈服应力不一致引起的,并提出了有效剪切速率的概念,阐述了扭矩在初始剪切时间段内下降的机理。而ROUSSEL等[10]从颗粒之间的关系出发,认为引起水泥基料浆触变性的原因有两个:一是早期水化反应生成的水合物;二是颗粒絮凝成团作用产生的结构性絮团。在此基础上,LOWKE等[11]认为浆体中固液之间的相互作用及水化反应都会阻碍颗粒之间的分离,而触变性的大小与这种相互作用及水化反应的剧烈程度呈正相关,并针对性地提出了能够定性描述触变性的数学模型。杨柳华等[7]也认为全尾砂颗粒以三维网状结构弥散与空间,料浆的触变性与屈服应力和料浆稳定性有关。但是,上述研究均是尝试解释触变性的本质,较少涉及触变性的影响因素及外在表现,而且,LOWKE等[11]提出的模型缺乏定量分析的功能。为此,本文以室内流变实验为基础,结合量纲分析理论,研究充填料浆触变性的影响因素及外在表现,并尝试提出定量描述触变性的预测模型,阐述触变性的一般机理。
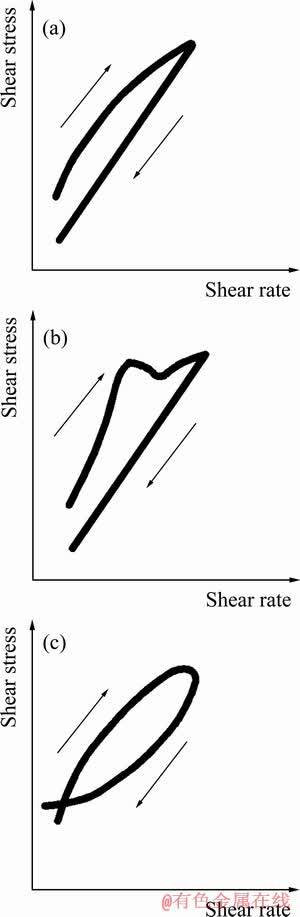
图1 常见触变环形态
Fig. 1 Common thixotropic ring morphology
1 实验
1.1 实验材料与设备
尾砂选用某矿分级尾砂,经实验室测试,尾砂密度为2.62 t/m2,经过NKTG100-D型激光粒度仪测试,尾砂粒级组成结果如图2所示。由图2可知,粒径<74 μm的尾砂占到90%以上,中值粒径约为15 μm。水泥采用的是P.O 32.5普通硅酸盐水泥,中值粒径约为9μm。实验用水为城市自来水。触变性测试采用美国赛默飞HAAKE Viscotester iQ流变仪,转子型号为FL22,测试设备见图3。
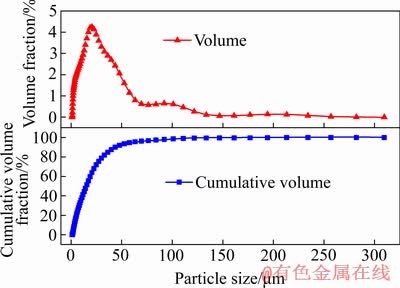
图2 尾砂粒级分析
Fig. 2 Grain size analysis of tailings
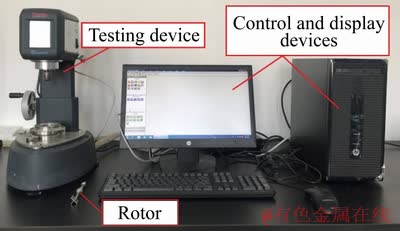
图3 触变性测试设备
Fig. 3 Thixotropy test equipment
1.2 实验方案
经过前期探索实验,在保证料浆流动性的前提下,针对质量浓度为60%、62%、64%,灰砂比为1:4、1:6、1:8的料浆设计两因素三水平全面实验,共计9组,实验方案见表1。
剪切实验中,采用控制剪切速率(CR)的方法,剪切速率先从0经过200 s的时间均匀上升至100 s-1,然后在200 s内由100 s-1均匀降低至0,每组实验过程共计400 s,其剪切速率与时间关系如图4所示。
表1 充填料浆剪切触变实验方案
Table 1 Experimental scheme of shear thixotropy of filling slurry
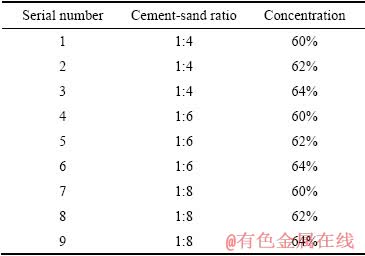
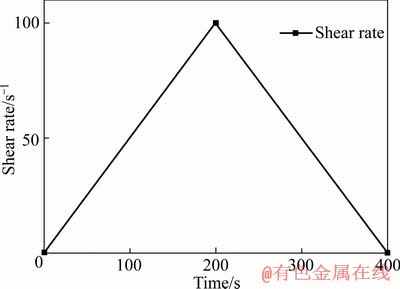
图4 浆料的剪切速率与时间关系
Fig. 4 Relationship between shear rate and time of slurry
2 结果与讨论
2.1 触变形态分析
实验结束后,运用Origin绘制剪切应力-剪切速率关系曲线图,并计算触变环封闭区域面积,用Athix表示,其中,上行曲线与下行曲线出现多于两个交点时,计算各部分封闭区域面积并求和,计算结果见 图5。从图5(a)和(b)中可看出,料浆质量浓度为60%和62%时,六组触变环形态与图1(a)较符合。由于这两个浓度相对较低,固体颗粒含量相对少,水作为载体能充分发挥协同作用,剪切时颗粒之间的絮凝成团行为相对较弱,均质性始终维持在较好的水平,导致上行曲线与下行曲线为简单上升与下降,一般不超过两个交点。由图5(c)可看出,质量浓度为64%的3组料浆触变环形态与图1中任意一种情况都不完全符合,剪切初期会发生类似图1(b)中的应力超调现象;原因是随着浓度的增加,固体颗粒占比增加。此时超细颗粒和水同时承担载体作用,颗粒间的絮凝成团行为相对较强,均质性下降,剪切致使结构破坏以后,表现出剪切应力波动较大的现象,但在此实验条件下,此时的剪切速率并不低,因此,后续未能出现图1(c)中的现象,导致上行曲线与下行曲线会出现多于两个交点,触变环形态独自呈一类。
2.2 浓度、灰砂比对触变性的影响
不同质量浓度与不同灰砂比对Athix值的影响见 图6。由图6(a)可看出,在任一确定灰砂比的条件下,Athix值均会随着质量浓度的升高而增大,且随着浆体中固体质量分数的升高;这种Athix值的增大呈非线性趋势,表现为质量浓度由62%增至64%时,Athix值的增幅比质量浓度由60%增至62%的增幅高;这种梯度增长是因为随着固体含量的持续升高,料浆呈现更明显的非牛顿流体特性,同时流动性有所降低,剪切造成的结构改变不能及时自愈造成的。另外,从图6(a)中还可看出,灰砂比为1:4时,这种梯度增长性明显强于灰砂比为1:6与1:8时的情况,说明在固体含量一定的条件下,水泥比尾砂更容易引起料浆絮团结构的改变。由图6(b)可见,在任一确定质量浓度的情况下,Athix值同样会随着水泥掺量的增加而增大,且呈现跟图6(a)中相似的非线性趋势;但灰砂比改变的仅是水泥的掺量,并不改变料浆中总固体质量分数的大小。因此,这种Athix值的增加并非由“量”的改变而产生的,而是因为水泥在料浆中是以超细颗粒和水化反应的“双重身份”对料浆的絮团结构产生了影响,从而降低了结构自愈性,增大了Athix值。
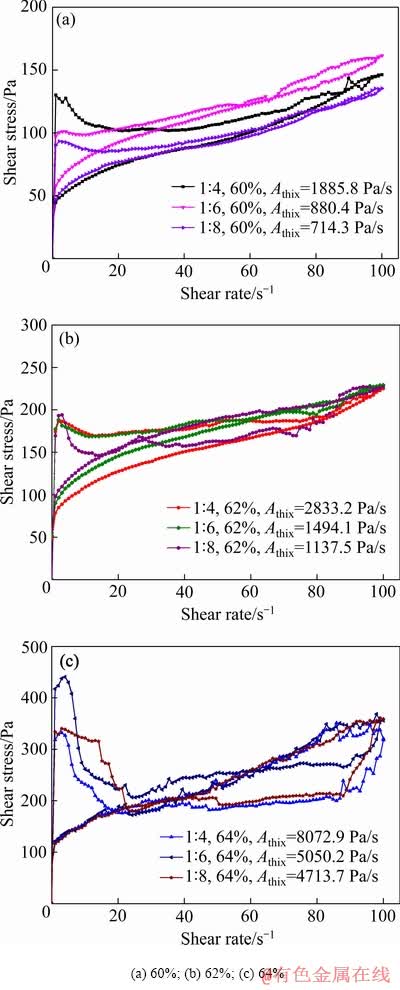
图5 各组实验触变环形态及Athix值(以质量浓度区分)
Fig. 5 Thixotropic ring morphology and Athix values (Distinguished by concentration)
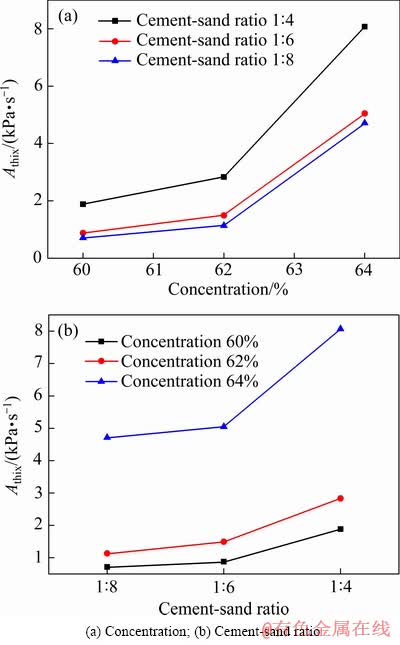
图6 质量浓度、灰砂比对Athix值的影响
Fig. 6 Effects of concentration and cement-sand ratio on Athix values
2.3 表观黏度的表现
触变的本质是表观黏度跟随剪切不断做适应性变化如图7所示。由图7可看出,9组料浆表观黏度在时间上的变化具有相似性,基本可以概括为以下3个阶段:第一,下降阶段,在较短时间内,从较高的初始值迅速降低至较低值,这是因为在料浆制备的搅拌过程中,会有一定的絮凝成团行为发生,但这种絮团的结构是不稳定的,在剪切发生后迅速发生破坏,引发表观黏度急剧下降,即所谓的剪切变稀;第二,稳定阶段,较长时间稳定在该较低的值上,这段时间占据总剪切时间的75%左右,由于该阶段内絮团结构的破坏与再生达到平衡,所以表观黏度的值较为稳定;第三,上升阶段,表观黏度迅速升高,升高后的值比稳定阶段高,但回不到初始值水平。这是因为随着剪切速率的降低,絮团结构的再生速率大于破坏速率,所以引起表观黏度的上升;但由于再生时间内始终伴随着或大或小的结构破坏行为,因此,在剪切结束瞬间,黏度不能立即恢复到初始值水平。
图8所示为黏度初始值与最终值之间的差值,其中,表观黏度降低最多的是灰砂比1:6、质量浓度64%的料浆,降幅达到71%;最少的是灰砂比1:6、质量浓度60%的料浆,降幅为40.1%。这与Athix值的大小规律(最大组为灰砂比1:4、质量浓度64%的料浆,最小组为灰砂比1:8、质量浓度60%的料浆)并不一致,其原因是触变环面积的实质是剪切速率与剪切应力乘积的积分差,因此虽然表观黏度的适应性变化是触变性的流变表现,但视表观黏度的变化等同于触变性是不客观的。
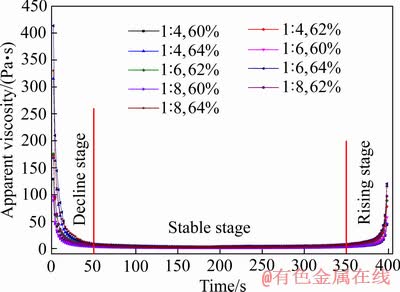
图7 表观黏度-时间关系
Fig. 7 Relationship between apparent viscosity and time
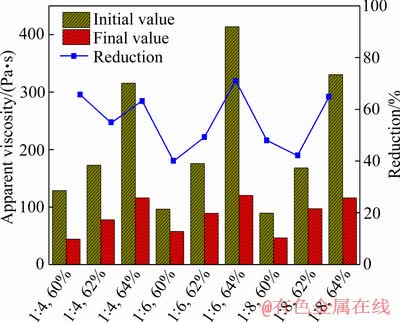
图8 表观黏度初始值与最终值对比
Fig. 8 Comparison between initial value and final value of apparent viscosity
2.4 剪切应力的表现
每组实验过程为400 s,在200 s处为剪切速率由上升变为下降的转折点。图9所示为9组料浆剪切过程中剪切应力随时间的变化曲线。
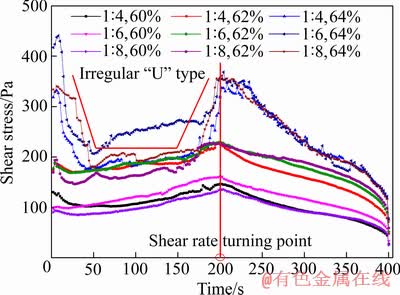
图9 剪切应力与时间关系
Fig. 9 Relationship between shear stress and time
由图9可见,质量浓度为60%和62%时,应力与时间的曲线基本以剪切速率转折点为中心,呈左右对称,且左右两部分分别呈单调增和单调减的趋势;其原因如前所述,剪切对象均质性较好,导致应力波动较小。而质量浓度为64%的三组,应力均明显表现出先上升后下降的现象,并在接下来一段较长时间表现平稳,在剪切速率转折点前又迎来上升,呈现不规则“U”字型;但在转折点后,会平稳下降,跟其他两个浓度一样,在实验结束后,收敛于一个较低值。这种“U”字型的前半段,是由于静态屈服应力和动态屈服应力不一致导致的;在CR的前提下,当剪切发生时,意味着原有的结构遭到破坏,料浆开始流动,此时的应力值便是静态屈服应力,随着剪切速率的增加,结构的破坏与再生达到平衡;该时的应力值是动态屈服应力,由此也可得出,静态屈服应力大于动态屈服应力。“U”字型的后半段是由于在转折点之前平衡早已达成,但剪切速率一再增加,转子的扭矩必然增加,根据牛顿第三定律可得,应力必然增加,从而呈现了完整的不规则“U”字型。
3 预测模型及评价
3.1 量纲齐次性原理
一个物理过程能用正确反映其客观规律的数学方程表述时,方程中每一项的量纲应该是和谐的、一致的;如果将方程中各项的量纲均用基本量纲的幂的形式来表示,那么,各项的基本量纲必须齐次[12-13]。
3.2 推导过程
结合国内外学者的研究结果[14-19],考虑剪切时浆体微观结构和流变性能的变化,可得出在触变性实验中,触变性Athix与以下5个因素有关:动态屈服应力、塑性黏度、密度、固体颗粒的中值粒径、最大剪切速率。则触变性Athix便可写成上述5个因素的函数,即
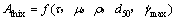 (1)
(1)
式中: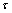 为动态屈服应力;
为动态屈服应力;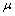 为塑性黏度;
为塑性黏度;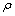 为密度;d50为固体颗粒的中值粒径;
为密度;d50为固体颗粒的中值粒径;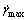 为最大剪切速率。
为最大剪切速率。
上述公式中涉及到6个物理量的量纲分别为
 (2)
(2)
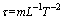 (3)
(3)
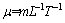 (4)
(4)
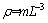 (5)
(5)
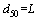 (6)
(6)
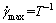 (7)
(7)
选用m(质量)、L(长度)、T(时间)为基本量纲,从上述6个物理量中选取分别包含m、L、T这3个基本量纲的密度、中值粒径、最大剪切速率作为基本物理量,经验证,该3个基本物理量的三阶行列式不为0,即相互独立,那么根据π定理,Athix、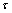 、
、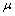 便可写成由3个基本物理量的指数乘积形式表示的无量纲量,即
便可写成由3个基本物理量的指数乘积形式表示的无量纲量,即
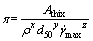 (8)
(8)
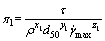 (9)
(9)
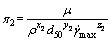 (10)
(10)
将式(2)、(5)、(6)、(7)代入式(8),得
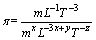 (11)
(11)
根据量纲齐次性原理,π是无量纲量,即
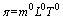 (12)
(12)
联立式(11)、(12)可得
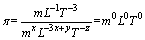 (13)
(13)
即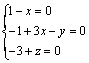 ,经计算得到
,经计算得到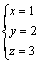 ,确定了x、y、z的值后,就可以写出π的具体表达式,为
,确定了x、y、z的值后,就可以写出π的具体表达式,为
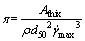 (14)
(14)
同理可求得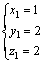 ,
, ,那么π1、π2的表达式分别为
,那么π1、π2的表达式分别为
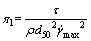 (15)
(15)
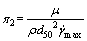 (16)
(16)
则式(1)可改成
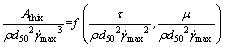 (17)
(17)
将式(17)变形为
 (18)
(18)
令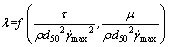 ,那么式(18)变为
,那么式(18)变为
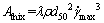 (19)
(19)
定义λ为触变系数,由该料浆的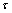 、
、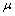 、
、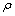 、d50、
、d50、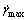 共同决定,此时,通过实验即可确定λ的变化规律,从而导出该料浆的触变性预测模型。
共同决定,此时,通过实验即可确定λ的变化规律,从而导出该料浆的触变性预测模型。
3.3 适用性评价
将剪切实验中各相关数据带入式(19),求解各组相对应的λ。实验中各组相关数据及λ计算结果见表2。
对λ进行5个影响因素的回归分析,回归方程见式(20),复相关系数为0.9904,P值为0.004,在检验标准0.05以下,说明相关性极好。
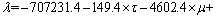
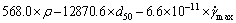 (20)
(20)
从式中各因素的系数可以看出,对触变系数λ影响最大的因素为中值粒径d50,但是相关性为负相关,即中值粒径越大,触变系数λ就越小。而由式(19)中λ的定义可知,λ与Athix值呈正相关,综上可得出结论,中值粒径越大,触变环的面积越小。同理可判断出对Athix值的影响水平排序,在中值粒径之后,由大到小依次为:塑性黏度,负相关;其次为料浆密度,正相关;再次为动态屈服应力,负相关;最后为最大剪切速率,负相关。
针对某一固定料浆而言,其动态屈服应力、塑性黏度、密度、中值粒径均为其固有属性,仅有最大剪切速率为随工况而改变的变量,只要确定一个最大剪切速率,即可通过预测模型计算料浆的触变性。
为验证预测模型的适用性,选取质量浓度与灰砂比两两各不相同的3组实验,分别为:灰砂比1:4、浓度60%,灰砂比1:6、浓度62%,灰砂比1:8、浓度64%。设计最大剪切应力为110 s-1的实验,实验结束后运用Origin计算Athix值,同时运用式(19)、(20)计算Athix值,将该值与Origin计算值做对比,结果见图10。
表2 剪切实验各组相关数据
Table 2 Relevant data in shear experiments

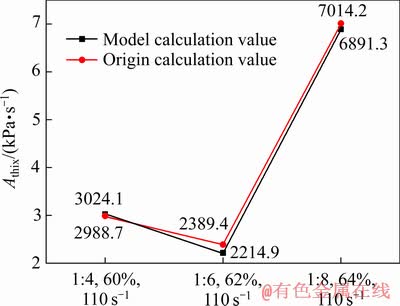
图10 模型与Origin计算值对比
Fig. 10 Comparison values of calculation between prediction model and Origin
由图10可知,3组验证性实验的误差分别为4.6%、7.9%、6.1%,平均误差率为6.2%,说明该模型的适用性良好,可以在已知料浆固有属性的前提下,针对不同工况预测料浆的触变能力,在工程应用当中是十分有益的,具有一定的推广意义。
4 结论
1) 剪切触变实验中,60%、62%质量浓度料浆触变环形态,与现有常见均质性浆体触变环形态比较接近,而质量浓度为64%料浆剪切应力的波动范围,比60%、62%浓度料浆的波动范围大,上行曲线与下行曲线会出现多于两个交点,造成其触变环形态与其他实验组不同,单独呈一类。
2) 充填料浆的触变性与质量浓度和灰砂比均呈正相关,且具有梯度增长型非线性特点,相同固体质量分数的条件下,水泥比尾砂对触变性的影响水平更高。
3) 表观黏度会在剪切过程中表现出3个阶段:下降阶段,稳定阶段和上升阶段。其中,下降阶段与上升阶段发生较为迅速,而稳定阶段维持时间较长,占据总剪切时间的75%左右,剪切结束瞬间的表观黏度低于初始表观黏度,且组与组之间黏度降低幅度的规律与触变环面积的大小规律并不一致。
4) 质量浓度为60%、62%的料浆,剪切应力基本以剪切速率转折点为中心左右对称,左右两侧分别为较为规整的单调增与单调减;质量浓度为64%的料浆剪会在转折点前呈现出不规则的“U”字型。
5) 基于量纲齐次性原理推导了触变性预测模型,经实验检验,平均误差率为6.2%,适用性良好,具有一定的推广意义。
REFERENCES
[1] TAN Yuan-qiang, CAO Guo-dong, ZHANG Hao, WANG Jia-qian, DENG Rong, XIAO Xiang-wu, WU Bin-xing. Study on the thixotropy of the fresh concrete using DEM[J]. Procedia Engineering, 2015, 102: 1944-1950.
[2] LANDROU G, BRUMAUD C, PLOTZE M L, WINNEFELD F, HABERT G. A fresh look at dense clay paste: Deflocculation and thixotropy mechanisms[J]. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 2018, 539: 252-260.
[3] 颜丙恒, 李翠平, 吴爱祥, 王少勇, 侯贺子. 膏体料浆管道输送中粗颗粒迁移的影响因素分析[J]. 中国有色金属学报, 2018, 28(10): 2143-2153.
YAN Bing-heng, LI Cui-ping, WU Ai-xiang, WANG Shao-yong, HOU He-zi. Analysis on influence factors of coarse particles migration in pipeline transportation of paste slurry[J]. The Chinese Journal of Nonferrous Metals, 2018, 28(10): 2143-2153.
[4] RINALDI V A, CLARIA Jr J J. Time dependent stress–strain behavior of bentonite slurries; effect of thixotropy[J]. Powder Technology, 2016, 291: 311-321.
[5] SANTOS F N, DE SOUSA S R G, BOMBARD A J F, VIEIRA S L. Rheological study of cement paste with metakaolin and/or limestone filler using mixture design of Experiments[J]. Construction and Building Materials, 2017, 143: 92-103.
[6] MA Si-wei, QIAN Ye, KAWASHIMA S. Experimental and modeling study on the non-linear structural build-up of fresh cement pastes incorporating viscosity modifying admixtures[J]. Cement and Concrete Research, 2018, 108: 1-9.
[7] 杨柳华, 王洪江, 吴爱祥, 邢 鹏, 高维鸿. 全尾砂膏体搅拌剪切过程的触变性[J]. 工程科学学报, 2016, 38(10): 1343-1349.
YANG Liu-hua, WANG Hong-jiang, WU Ai-xiang, XING Peng, GAO Wei-hong. Thixotropy of unclassified pastes in the process of stirring and shearing[J]. Chinese Journal of Engineering, 2016, 38(10): 1343-1349.
[8] MEWIS J, WAGNER N J. Thixotropy[J]. Advances in Colloid and Interface Science, 2009, 147: 214-227.
[9] QIAN Y, KAWASHIMA S. Distinguishing dynamic and static yield stress of fresh cement mortars through thixotropy[J]. Cement and Concrete Composites, 2018, 86: 288-296.
[10] ROUSSEL N, OVARLEZ G, GARRAULT S, BRUMAUD C. The origins of thixotropy of fresh cement pastes[J]. Cement and Concrete Research, 2012, 42(1): 148-157.
[11] LOWKE D. Thixotropy of SCC—A model describing the effect of particle packing and superplasticizer adsorption on thixotropic structural build-up of the mortar phase based on interparticle interactions[J]. Cement and Concrete Research, 2018, 104: 94-104.
[12] 谢振华. 工程流体力学[M]. 第4版. 北京: 冶金工业出版社, 2013: 201-205.
XIE Zhen-hua. Engineering fluid mechanics[M]. 4th ed. Beijing: Metallurgical Industry Press, 2013: 201-205.
[13] 李雨成, 刘天奇, 周西华. 基于量纲分析理论的煤尘爆炸能量预测模型[J]. 爆炸与冲击, 2017, 37(3): 566-570.
LI Yu-cheng, LIU Tian-qi, ZHOU Xi-hua. An energy prediction model for coal dust explosion based on dimensional analysis[J]. Explosion and Shock Waves, 2017, 37(3): 566-570.
[14] PEREZ-JIMENEZ F E, BOTELLA R, MIRO R. Differentiating between damage and thixotropy in asphalt binder’s fatigue tests[J]. Construction and Building Materials, 2012, 31: 212-219.
[15] ASSAAD J J, ISSA C A. Preliminary study on interfacial bond strength due to successive casting lifts of self-consolidating concrete—Effect of thixotropy[J]. Construction and Building Materials, 2016, 126: 351-360.
[16] 刘晓辉, 吴爱祥, 王洪江, 焦华喆, 刘斯忠, 王少勇. 全尾膏体触变特性实验研究[J]. 武汉理工大学学报(交通科学与工程版), 2014, 38(3): 539-543.
LIU Xiao-hui, WU Ai-xiang, WANG Hong-jiang, JIAO Hua-zhe, LIU Si-zhong, WANG Shao-yong. Experimental studies on the thixotropic characteristics of unclassified-tailings paste slurry[J]. Journal of Wuhan University of Technology(Transportation Science & Engineering), 2014, 38(3): 539-543.
[17] 霍海峰, 齐 麟, 雷华阳, 于 鸽. 天津软黏土触变性的思考与试验研究[J]. 岩石力学与工程学报, 2016, 35(3): 631-637.
HUO Hai-feng, QI Lin, LEI Hua-yang, YU Ge. Analysis and experimental study on thixotropy of Tianjin soft clay[J]. Chinese Journal of Rock Mechanics and Engineering, 2016, 35(3): 631-637.
[18] 吴爱祥, 程海勇, 王贻明, 王洪江, 刘晓辉, 李公成. 考虑管壁滑移效应膏体管道的输送阻力特性[J]. 中国有色金属学报, 2016, 26(1): 180-187.
WU Ai-xiang, CHENG Hai-yong, WANG Yi-ming, WANG Hong-jiang, LIU Xiao-hui, LI Gong-cheng. Transport resistance characteristic of paste pipeline considering effect of wall slip[J]. The Chinese Journal of Nonferrous Metals, 2016, 26(1): 180-187.
[19] 王文孟, 郭少春, 崔自治. 可溶盐对黄土触变性的作用效应研究[J]. 岩土力学, 2014, 35(12): 3385-3388, 3395.
WANG Wen-meng, GUO Shao-chun, CUI Zi-zhi. Study of effect of soluble salt on loess thixotropy[J]. Rock and Soil Mechanics, 2014, 35(12): 3385-3388, 3395.
Experiment of shear thixotropy of cemented tailings filling slurry and its prediction model based on dimensional analysis
ZHANG You-zhi1, GAN De-qing1, CHEN Xun2, XUE Zhen-lin1, REN Wei-cheng1
(1. College of Mining Engineering, North China University of Science and Technology, Tangshan 063210, China;
2.School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China)
Abstract: The thixotropic behavior of filling slurry with different concentration and cement-sand ratio was studied by paddle rheometer. The thixotropy prediction model based on dimensional analysis was proposed. The results show that the thixotropic morphologies of slurry with different concentration are different, and the shear stress of slurry with high concentration is more fluctuating. The thixotropy is positively correlated with concentration and cement-sand ratio, and the cement can induce thixotropy more than tailings. During the shear process, the apparent viscosity first decreases rapidly, then maintains stable, and finally rises sharply, but the final value is less than the initial value. The shear stress of the slurry with mass concentration of 64% presents an irregular “U” shape before the turning point while the other groups, however, are basically symmetric around the turning point. The experiments are designed to verify the prediction model, and the results show that the average error rate is 6.2%, with good adaptability.
Key words: filling slurry; shear; thixotropic behavior; dimensional; prediction model
Foundation item: Project(51774137) supported by the National Natural Science Foundation of China; Projects (E2016209220, E2019209326) supported by the Natural Science Foundation of Hebei Province, China
Received date: 2019-04-04; Accepted date: 2019-07-02
Corresponding author: GAN De-qing; Tel: +86-315-8805400; E-mail: gdqheut@163.com
(编辑 李艳红)
基金项目:国家自然科学基金资助项目(51774137);河北省自然科学基金资助项目(E2016209220, E2019209326)
收稿日期:2019-04-04;修订日期:2019-07-02
通信作者:甘德清,教授,博士;电话:0315-8805400;E-mail:gdqheut@163.com