基于3DFR算法的爆破块度图像处理研究及其应用

赵国彦¹，戴兵¹，马驰¹，张雷²，王珊¹

(1. 中南大学 资源与安全工程学院，湖南 长沙，410083；

2. 广西大学 计算机与电子信息学院，广西 南宁，530004)

摘要：考虑地下矿山拍照时的低对比度、噪声的干扰及灰度的不确定性等因素的特殊条件，提出适合地下矿山大块率测定的3DFR算法图像处理技术：首先，根据概率论确定三维直方图中目标与背景的区域；然后，通过模糊熵求极大值原理选取三维阈值，进而对图像进行处理；选取9组关于爆破块度的照片进行分割处理，并与OTSU法和传统方法进行分割结果对比评价。为了进一步考察3DFR算法图像处理技术的准确性，与现场实际测量结果进行对比和相关性分析。研究结果表明：3DFR算法图像处理结果与现场实际测量结果较吻合，相关性系数达到0.955，为地下矿山爆破大块率安全、准确、高效的测定提供了一条途径，并可用于地下矿山爆破参数优化。

关键词：爆破块度；3DFR算法；图像分割；最佳阈值

中图分类号：TD315           文献标志码：A         文章编号：1672-7207(2013)05-2002-06

Research and application on blasting fragmentation image processing based on 3DFR algorithm

ZHAO Guoyan¹, DAI Bing¹, MA Chi¹, ZHANG Lei², WANG Shan¹

(1. School of Resources and Safety Engineering, Central South University, Changsha 410083, China;

2. School of Computer, Electronics and Information, Guangxi University, Nanning 530004, China)

Abstract: Considering the problems of the low contrast, noise interference and gray uncertainty appears when taking pictures of the underground mine, the processing technology of 3DFR algorithm was put forward to suit the rock fragment rate in the underground mine. The procedures were as follows: Firstly, the target and setting in three-dimensional histogram were determined according to the probability theory. Then, according to the fuzzy entropy and the maximum principle, three-dimensional threshold was selected, and the images were disposed. Nice groups of blasting fragment photos were selected for analysis by OTSU method, traditional method and 3DFR method. Comparison and correlation analysis between the analysis results and the measured results were deduced to study the veracity of the processing technology of 3DFR algorithm. The results show that the correlation coefficient between the analysis results and the measured results is 0.955, which provides a way for safe, accurate and efficient determination of the blasting fragment rate of the underground mine and provides guidance for optimization of blasting parameters of the underground mine.

Key words: blasting fragmentation; 3DFR algorithm; image segmentation; optimal threshold

随着社会的发展，现代矿山为了增大产量，基本上都采用中深孔爆破。而爆破后的大块率则是评价爆破效果的最主要指标，也是爆破参数优化的重要参考依据。目前，人们对爆破大块率的测定技术进行了大量研究。评价爆破大块有以下几种方法：筛选法、大块计数法、现场直接法及照相法^[1]。由于采用前3种方法非常费时、耗力且存在较大的安全隐患，因此，照相法应用得比较普遍。照相法主要采用图像处理技术，图像处理是指将图像信号转换成数字信号并利用计算机对其进行处理的过程^[2-5]。国内外学者对此进行了广泛研究，提出了很多算法，如Otsu^[6]的动态门限法。该法利用图像的灰度直方图，以目标和背景之间的方差最大为目标，动态地确定图像的分割门限值。Pun^[7]采用信息论中熵的概念进行图像分割的阈值选取，提出了基于信息熵的阈值分割方法。1982年Johannsen等^[8]提出了一种利用信息测度来度量图像分割中的目标信息和背景信息的相关程度并要求其最小的方法来选取阈值。Kaput等^[9]在1985年提出了最大熵阈值法。该熵阈值法采用系统内部均匀性假设，且利用图像灰度概率信息，因而在医学、军事等方面应用较广。由于在地下矿山条件下照相受噪声等因素干扰严重，使得许多情况下目标岩块和背景的分布相互重叠不可区分，采用熵阈值法不能获得满意的分割效果，因此，有必要针对地下金属矿山爆破岩块图像分割提出一种新的分割方法。本文作者从医学细胞识别方面借鉴基于模糊划分熵的阈值分割方法^[10-12]，提出结合模糊理论和概率论的新方法即3DFR算法，它根据模糊熵求极大值原理选取三维阈值，进而对图像进行处理。

1  算法原理的描述

1.1  三维直方图的建立

设图像的尺寸为m×n，图像像素点的灰度变化范围为0到L-1，则像素点(x, y)的邻域均值灰度为^[10]

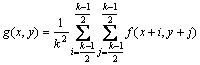        (1)

其中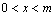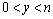：, ；k为象元点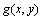的正方形邻域窗口的宽度。对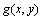于，由于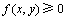，故下列等式成立：

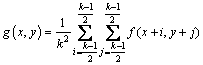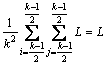＜              (2)

即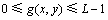。因此，邻域平均灰度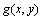与图像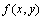具有同样的灰度变化范围。

同理，定义像素点(x, y)的邻域灰度中值为

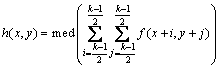       (3)

其中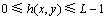：，邻域中值灰度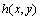)也与图像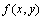)具有同灰度变化范围；“med”表示取中值。

对于任意1幅图像，可以用矩阵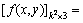 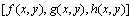表示：

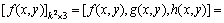
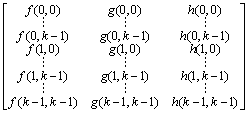   (4)

对于1幅m×n的灰度图像，采用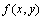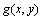，和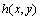的向量表示式定义它的三维直方图的3个坐标，该三维直方图定义在L×L×L的正方体区域，其3个坐标分别表示图像像素点的灰度、邻域均值灰度、邻域中值灰度。直方图中的任意1点定义为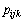,它表示向量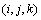出现的频率。

如图1所示为图像的三维直方图。其中：图1(a)所示给出了三维直方图的定义域，通过阈值(a，b，c)，可以分割成图1(b)的8个立方体区域。显然，三维直方图中存在着与目标O和背景B相对应的2类区域。它们有不同的概率分布，利用三维直方图的任意阈值(a, b, c)对图像进行分割，目标和背景2类区域内发生的概率分别为：

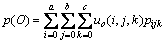         (5)

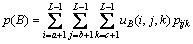        (6)

1.2  最大模糊熵的分割

假设图像由目标域O和背景域B组成，目标的隶属度函数用Z函数^[13]表示。O和B的隶属函数分别为：

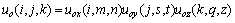     (7)

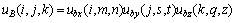     (8)

式中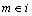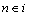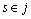：，；，，为任意点，且满足，， 。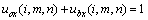

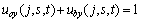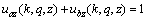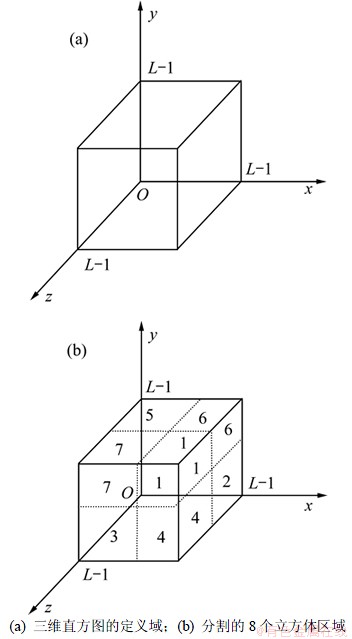
图1  图像的三维直方图

Fig.1  Three-dimensional histograms of image

基于此，推导出三维直方图的最大模糊熵表达式为

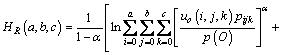
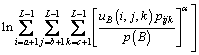      (9)

当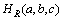取得最大值时所对应的阈值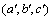即为最佳阈值，目标和背景分离得最好，此时图像的分割效果最佳。因此，阈值选择即为寻找最佳参数对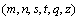使得式(9)取得最大：

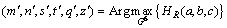。利用求得的最佳阈值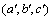对图像进行分割。

2  实例分析

用沙坝矿某实验采场中深孔爆破后对爆堆的各个面进行数码拍照，以获得爆破矿石的原始图像，见图2。拍照时应注意：首先，要保证光线充足，拍摄区域不能留下黑暗区；其次，要确定照相的区域大小，并尽量保证每个地方的投影比例相同；相机应与拍摄面保持垂直。完成现场照相后，对图像进行预处理，用photoshop7.0软件对照片进行格式转换并确定照片尺寸，再根据前面的分析对处理后的照片基于3DFR算法对图像进行分割。照片大小为100×90，利用前面的公式并结合Matlab编程计算出最佳阈值为(91, 115, 141)。当a在0~1之间时的图像分割效果比较理想^[14]，因此，这里选择a=0.5来处理照片。经3DFR方法处理后的矿石图像见图3。为了增加对比性，在此选用OTSU算法和传统算法的图像处理方法对照片进行分割处理，如图4和图5所示。

2.1 分割结果评价分析

由于图像信息较复杂，因此，在此选用实验优度法^[15-16]来进行评价，主要考虑要参数区域的内部均匀性U_M、区域对比度G_C、形状测度S_M和模糊度D。具体评价模型如下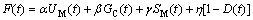^[10]：

   (10)

其中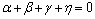：。F(t)越大，说明分割的质量越好。在实验中选择3次爆破图片，并选用3DFR和OTSU算法与传统算法的图像处理方法对其进行处理和评价。各参量值及评价结果如表1和图6所示。

图2  原始图像

Fig.2  Original image

图3  3DFR方法处理后图像

Fig.3  Image processed by 3DFR method

图4  OTSU方法处理后图像

Fig.4  Image processed by OTSU method

图5  传统方法处理后图像

Fig.5  Image processed by traditional method

从表1可以看出：区域均匀性参数对图像分割影响不明显，而评价结果受对比度和模糊度的影响较明显。结合图6可知：3DFR的分割性能较优越，评价结果指标较高；OTSU方法能将图片中较大部分目标分割出来，但不能区分小部分目标和背景像素，因而评价结果较低；而传统方法只能分割对比度较高且目标较大的图像，丢失了绝大部分像素，所以，误差较大。经综合考虑，3DFR方法能较准确地反映真实爆破块度。

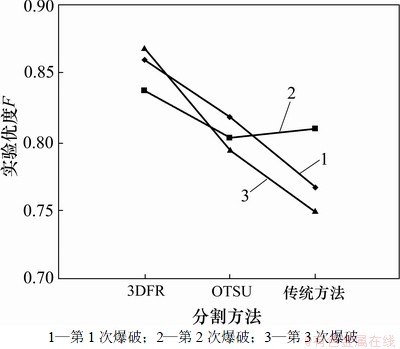
图6  3种分割方法对应的评价结果

Fig.6  Corresponding results of evaluation using three segmentation methods

2.2  试验结果分析

对于采用3DFR方法处理后的图像，获取其几何特征。爆破后岩块的几何特征包括面积、周长、宽度、高度等。在此，采用基于几何特征的图像识别方法^[17]来获得岩块的几何特征量，如表2所示。

通过现场标准岩块图像的比例换算，定义面积大于180 000像素的岩块就判定为大块。由表2可知：大块总面积(面积大于180 000像素的岩块相加得到的大块总的面积)为1 817 950像素，测量区域面积(所有块度面积之我)为13 996 800像素。于是，得到测量区域的大块率为12.98%，而现场测量的大块率为13.34%。将9次爆破后的照片采用以上分析方法进行处理分析与现场测量的数据结果进行比较，结果见表3。

表1  各参量值及评价结果

Table 1  Value of various parameters and results of evaluation

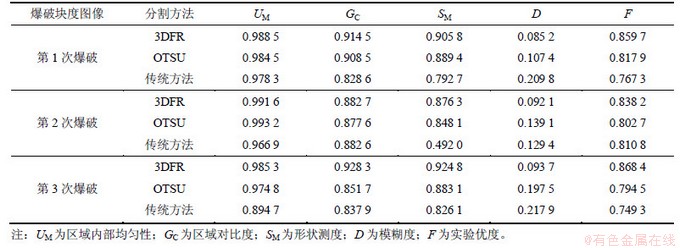
表2  岩块几何特征

Table 2  Geometry characteristic of rock block     像素

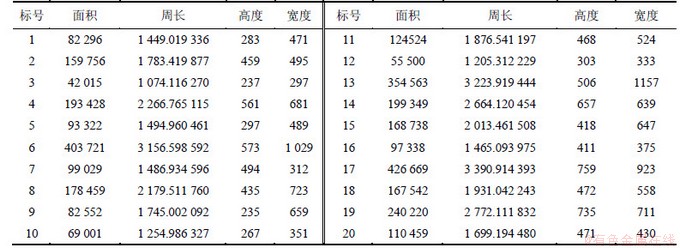
表3  图像测量与实际测量爆破大块率对比

Table 3  Image measurement and actual measurement results comparison      %

图7所示为实际测量和图像处理在9次爆破试验中得出的爆破大块率变化的对比曲线，图中曲线点对应值为实验平均值。由实际测量曲线和图像处理曲线对爆破大块率y与实验次数x进行相关分析，分别可得如下关系式：

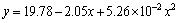        (11)

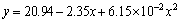        (12)

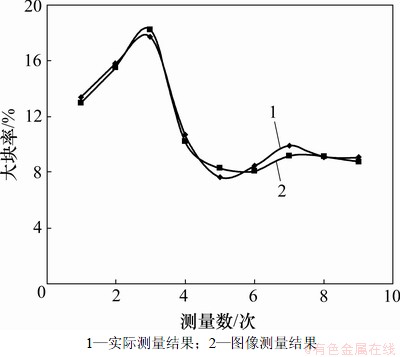
图7  2种方法对比曲线

Fig.7  Curves of comparison between two methods

对以上2个函数进行相关性分析，得出这2个函数的相关性系数为0.955，说明这2个函数有较高的相关程度，同时说明现场实际测量结果能够较好地验证基于3DFR算法的图像处理方法的结果，从而验证了本文方法的可行性和实用价值。

3  结论

(1) 提出了3DFR算法。该算法利用图像象元的灰度分布信息和邻域空间相关信息，包括邻域灰度中值信息和邻域灰度均值信息。借助图像的概率划分，给出算法表达式，从而可以得到最佳图像分割的阈值。

(2) 3DFR的分割性能较优越，评价结果指标较高。对处理后岩块的几何特征进行提取，以此来判定岩块是否属于大块。通过与现场实际测量结果进行对比和相关性分析，得到2个函数的相关性系数为0.955，表明采用该算法能够得到准确的分割结果，且具有较强的鲁棒性。

(3) 本算法对分析地下矿山大爆破后进行拍照时的低对比度、噪声的干扰及灰度的不确定性等方面具有一定的可行性和应用价值。由于此方法用于测量大块时具有安全、高效、低成本等优点，因此，可望成为测量爆破大块率的主要方法。

参考文献：

[1] 璩世杰. 平面照相法测定爆堆矿岩块度的原理及可靠性分析[J]. 爆破, 1991, 8(4): 52-55.

QU Shijie. Plane photography method for the determination of blasting pile ore block of the principle and reliability analysis[J]. Blasting, 1991, 8(4): 52-55.

[2] 张艳玲, 刘桂雄, 曹东, 等. 数字形态学在的基本算法及在图像预处理中的应用[J]. 科学技术与工程, 2007, 7(3): 356-360.

ZHANG Yanling, LIU Guixiong, CAO Dong. Basic operators of mathematical morphology and application in image preprocessing[J]. Science Technology and Engineering, 2007, 7(3): 356-360.

[3] 刘延保, 曹树刚, 刘玉成, 等. 应用支持向量机处理岩土材料的细观图像[J]. 重庆大学学报, 2008, 31(7): 720-725.

LIU Yanbao, CAO Shugang, LIU Yucheng. Application of a support vector machine to meso-structural image analysis of geomaterials[J]. Journal of Chongqing University, 2008, 31(7): 720-725.

[4] 曾万梅, 吴庆宪, 姜长生. 一种新的目标图像自适应阈值分割算法[J]. 电光与控制, 2009, 16(5): 27-30.

ZENG Wanmei, WU Qingxian, JIANG Changsheng. A new adaptive threshold method for target image segmentation[J]. Electronics Optics & Control, 2009, 16(5): 27-30.

[5] 雷博, 范九伦. 灰度图像的二维交叉熵阈值分割法[J]. 光子学报, 2009, 38(6): 1572-1577.

LEI Bo, FAN Jiulun. Two-dimensional cross-entropy thresholding segmentation method for gray-level images[J]. Acta Photonica Sinica, 2009, 38(6): 1572-1577.

[6] Otsu N. A threshold selection method from gray-level histogram[J]. IEEE Tram on System Man Cybernetics, 1979, 9(1): 62-66.

[7] Pun T. A new method for gray-level picture thresholding using the entropy of the histogram[J]. Signal Processing, 1980, 2(3): 223-237.

[8] Johannsen G, Bille J. A threshold selection method using information measures[J]. Proceedings of ICPR, 1982, 2(1): 140-142.

[9] Kaput J N, Sahoo P K A K C Wong. A new method for gray level picture thresholding using the entropy of histogram[J]. Computer Vision, Graphics and Image Processing, 1985, 29(3): 273-285.

[10] 刘锁兰. 基于模糊理论得图像分割区域法研究[D]. 南京: 南京理工大学计算机科学与技术学院, 2008: 26-37.

LIU Suolan. Study about methods based on fuzzy theory and region[D]. Nanjing: Nanjing University of Science and Technology. School of computer science and technology, 2008: 26-37.

[11] LU Jian, YE Zhongxing, ZOU Yuru, et al. An enhanced fractal image denoising algorithm[J]. Chaos, Solitons & Fractals, 2008, 38(4): 1054-1064.

[12] 景晓军, 李剑峰, 刘郁林. 一种基于三维最大类间方差的图像分割算法[J]. 电子学报, 2003, 31(9): 1281-1285.

JING Xiaojun, LI Jianfeng, LIU Yulin. Image segmentation based on 3-D maximum between-cluster variance[J]. Acta Electronica Sinica, 2003, 31(9): 1281-1285.

[13] Wang S T. Note on the equivalence relationship between Renyi- entropy based and Tsallis-entropy based image thresholding[J]. Pattern Recognition Letters, 2005, 26(14): 2309-2312.

[14] Sahoo P, Wilkins C, Yeager J. Threshold selection using Renyi’S entropy[J]. Pattern Recognition, 1997, 30(1): 71-84.

[15] 侯格贤, 毕笃彦. 图像分割质量评价方法研究[J]. 中国图像图形学报, 2000, 5(1): 39-43.

HOU Gexian, BI Duyan. Researches on evaluation methods for image segmentation[J]. Journal of Image and Graphics, 2000, 5(1): 39-43.

[16] 刘蔚琴, 凌捷. 敏感图像信息识别模型研究[J]. 计算机应用与软件, 2008, 25(6): 56-58.

LIU Weiqin, LING Jie. On sensitive image recognition model[J]. Computer Applications and Software, 2008, 25(6): 56-58.

[17] 陆玉亭. 基于图像分析的ABO血型识别方法研究[D]. 南京: 南京理工大学计算科学与技术学院, 2009: 44-47.

LU Yuting. Research about identification method based on the image analysis of ABO blood group[D]. Nanjing: Nanjing University of Science and Technology. School of Computer Science and Technology, 2009: 44-47.

(编辑  陈灿华)

收稿日期：2012-05-05；修回日期：2012-07-02

基金项目：国家重点基础研究发展规划(“973”计划)项目(2007CB209402)；国家重点实验室开放基金资助项目(SKLGDUEK0906)

通信作者：赵国彦(1963-)，男，湖南沅江人，博士，教授，从事采矿工程、矿山安全和岩石力学与工程的教学与研究工作；电话：13507311842；E-mail: 312929122@qq.com