J. Cent. South Univ. Technol. (2011) 18: 1235-1239

DOI: 10.1007/s11771-011-0827-y

Calculation of all-time apparent resistivity of large loop transient electromagnetic method with very fast simulated annealing

LI Jian-hui(李建慧), ZHU Zi-qiang(朱自强), FENG De-shan(冯德山),

XIAO Jian-ping(肖建平), PENG Ling-xing(彭凌星)

School of Earth Sciences and Info-physics, Central South University, Changsha 410083, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: In large loop transient electromagnetic method (TEM), the late time apparent resistivity formula cannot truly reflect the geoelectric model, thus it needs to define the all-time apparent resistivity with the position information of measuring point. Utilizing very fast simulated annealing (VFSA) to fit the theoretical electromagnetic force (EMF) and measured EMF could obtain the all-time apparent resistivity of the measuring points in rectangular transmitting loop. The selective cope of initial model of VFSA could be confirmed by taking the late time apparent resistivity of transient electromagnetic method as the prior information. For verifying the correctness, the all-time apparent resistivities of the geoelectric models were calculated by VFSA and dichotomy, respectively. The results indicate that the relative differences of apparent resistivities calculated by these two methods are within 3%. The change of measuring point position has little influence on the tracing pattern of all-time apparent resistivity. The first branch of the curve of all-time apparent resistivity is close to the resistivity of the first layer medium and the last branch is close to the resistivity of the last layer medium, which proves the correctness of the arithmetics proposed.

Key words: very fast simulated annealing (VFSA); large loop transient electromagnetic method; rectangular loop; all-time apparent resistivity

1 Introduction

The large loop transient electromagnetic method (TEM) mainly adopts rectangular loop as the transmitting source and considers the electromagnetic field in one-third of the area of the center of the loop as the uniform field. Therefore, one-time transmitting loop is usually deployed in the outdoors and multi-point measuring is conducted in one-third of the area of the center of the loop [1]. In fact, one-third of the area of the center of the rectangular loop is not a uniform field and the electromagnetic field varies with the positions of measuring points. As late-time apparent resistivity formula has no relations with the positions of measuring points, it is unable to calculate the apparent resistivity correctly. Thus, it needs to define the all-time apparent resistivity with the position information of measuring point.

In 1998, JIANG [1] calculated the all-time apparent resistivity with the least square method according to the electromagnetic field (EMF) expression stimulated by the rectangular loop in the homogeneous half-space surface deduced by Raiche. In 2005, XIONG [2] utilized the inverse spline interpolation for the calculation of all-time resistivity for the larger-loop transient electro- magnetic method, which laid the foundation for building the initial model in the automatic reversal development of transient electromagnetic method. In 2007, LI et al [3] considered the EMF generated by the arbitrary shape loop source as the sum of the vertical magnetic fields stimulated by many horizontal electric dipole sources, and then utilized the fitting method to get all-time apparent resistivity. In 2008, WANG [4] proposed that the transient response curve had translation and expansion features along with the underground electrical conductivity, the side length of transmitting loop and observation time, and came up with the all-time apparent resistivity translation algorithm. In 2009, ZHANG et al [5] utilized dichotomy to calculate the all-time apparent resistivity. They firstly computed the earliest all-time apparent resistivity and took this as the basis for computing the apparent resistivity at next moment, and then got the all-time apparent resistivity of all moments.

As the formulation of electromagnetic field stimulated by the rectangular loop is complicated, it is hard to utilize analysis method to deduce the explicit formulation [6-11] between the apparent resistivity and the transient electromagnetic field. Thus, it needs to use numerical method to compute the apparent resistivity of the measuring points in the rectangular loop. Based on the formulation of EMF excited by rectangular loop in any point of the earth surface, it is able to obtain all-time apparent resistivity by utilizing theoretical EMF and measured EMF. In this work, very fast simulated annealing (VFSA) that could obtain the global optimal solution is chosen as the fitting algorithm and TEM late time apparent resistivity is used to confirm the scope of the initial model.

Simulated annealing stems from statistical thermal physics. It stimulates the process that objects gradually cool down and reach the crystalline state under molten condition. In 1983, KIRKPATRICK et al used simulated annealing to solve global optimization problem. The simulated annealing has the following advantages: it does not need to compute Jacobian matrix, its computed results have little dependence on the initial model and it could get out of local extremum points to gain the globally optimal solution [12-14].

2 Very fast simulated annealing (VFSA)

The classical simulated annealing has low efficiency. Many scholars have modified the classical simulated annealing, among which the most typical ones are heat bath simulated annealing (HBSA) and VFSA. In this work, VFSA is adopted [15-18].

2.1 Simulated annealing criterion

It is supposed that the number of argument is X, noted as M={m_i|1≤i≤X}. The k-th iterative model is M^k and the objective function is Φ(M^k); and then the new model M^k+1 is randomly generated and the objective function is Φ(M^k+1). The following method is used to judge whether the new model M^k+1 is accepted:

ΔΦ=Φ(M^k+1)-Φ(M^k)                                                    (1)

P(ΔΦ)=exp(-ΔΦ/T)                                                     (2)

where T represents the temperature and is the controlling parameter. If ΔΦ≤0, it indicates that the objective function reduces and the new model is accepted unconditionally. If ΔΦ>0, it needs to compute P(ΔΦ) at first, and if 0R, the new model is accepted; conversely, the new model is not accepted and the model M^k+1 is generated.

As seen from Eqs.(1) and (2), the simulated annealing can both accept the new model in which the objective function reduces and the new model in which the objective function increases according to Eq.(2). When the temperature is high, the new model in which objective function increases is easy to be accepted, and it has the opportunity to jump out of local minimum and find out global minimum.

2.2 Generating new model and annealing strategy

The new model M^k+1 is adopted, which depends on temperature and is based on Cauchy distribution. For every parameter  it can be deduced that

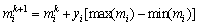              (3)

where max(m_i) and min(m_i) are the pre-confirmed upper limit and lower limit of the parameter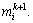  

The scope of y_i is between -1 and 1, which can be confirmed as

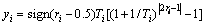                         (4)

where sign(?) is signum function and r_i is a random number between 0 and 1.

Different parameters could use different annealing strategies and different initial temperatures. T^k is determined by

                                                  (5)

where 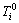 and  are the initial temperature and k-th temperature of m_i; c_i is a constant number and is set up by itself.

3 Forward formula and objective function

3.1 Forward formula

In the electromagnetic method, the apparent resistivity is deduced based on the electromagnetic field on the surface of homogeneous half-space medium. In large loop TEM, the vertical component expression formula [9] of impulse response of magnetic field stimulated by the rectangular transmitting loop paved on homogeneous half-space surface on the measuring point of earth surface at t moment is

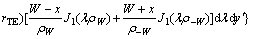    (6)

Equation (6) is derived from the rectangular coordinate system, of which, z axis is vertically downward and the origin of coordinate is in the center of rectangular loop. (x, y) indicates the measuring point coordinate; (x′, y′) indicates the small vertical magnetic dipole coordinate. L and W indicate the half-length and half-width of rectangular loop. ρ_L=[(x′-x)²+(L-y)²]^1/2, ρ_-L=[(x′-x)²+(-L-y)²]^1/2, ρ_W=[(W-x)²+(y′-y)²]^1/2, and ρ_-W=[(-W-x)²+(y′-y)²]^1/2. I is the transmitting current; 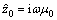 is the impedance analyzer in air; μ₀ indicates the permeability in air. r_TE is the reflection coefficient and the expression formula is

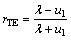                                                             (7)

There are under quasi-static condition. σ₁ and μ₁ indicate the conductivity and permeability of homogeneous half-space medium, respectively. λ is the wave number and ω is the angular frequency of electromagnetic wave. K_j is the coefficient of Gaver-Stehfest transform. In Eq.(6), -iω is replaced with j?ln2/t [19-20]; J₁ is the first-order Bessel function and uses Hankel transform to solve [21].

From Eq.(6), as the impulse response of magnetic field on the homogeneous half-space surface has complicated implicit function relations with conductivity, it is difficult to use analytic method to calculate the inverse function reflected by resistivity and impulse response of magnetic field. Thus, it has to use numerical approximation method to define apparent resistivity.

3.2 Objective function

In this work, VFSA is utilized to fit actually measured EMF and theoretical EMF (converted from impulse response of magnetic field) to compute the all-time apparent resistivity of rectangular transmitting loop of large loop TEM.

The objective function Ф(t, x, y) is

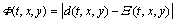                                 (8)

where d(t, x, y) and Ξ(t, x, y) indicate the actually measured EMF and theoretical EMF of point (x, y) at moment t, respectively.

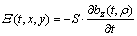                                             (9)

In Eq.(9), S indicates the equivalent area of receiver coil;  indicates the impulse response of magnetic field stimulated by rectangular transmitting loop paved on homogeneous half-space surface with resistivity of ρ in measuring point (x, y) at moment t.

4 Numerical calculations

Firstly, the EMF is stimulated by rectangular loop in the known surface of geoelectric model, and then VFSA is used to compute the all-time apparent resistivity of this geoelectric model.

4.1 Verification of algorithm

The correctness of the algorithm in this work is compared with the all-time apparent resistivity of the known geoelectric model calculated by WENG with dichotomy. The resistivities in layers of geoelectric model used by WENG are ρ₁=100 Ω?m, ρ₂=10 Ω?m and ρ₃=500 Ω?m, and the thicknesses of layers are h₁=400 m and h₂=50 m. The length and the width of transmitting loop is 600 m and 200 m and the positions of measuring points are (-260, -20) and (20, -20), respectively. It is noted that WENG places the origin of coordinate in the lower left of rectangular loop, while the authors of this article place the origin of coordinate in the geometric centre of rectangular loop. The parameters of VFSA are T₀=0.1, c=1 and X=1. The terminal condition is that the objective function is less than 1×10^-3. The scope of the initial model is confirmed in accordance with late time apparent resistivity. The initial value is 0.2-1.2 times of late time apparent resistivity.

Figure 1 shows the all-time apparent resistivities calculated with VFSA and WENG’s algorithm, respectively. From this figure, the plots of all-time apparent resistivities calculated by these two methods are very close, and the relative difference is less than 3%. For the two measuring points, the all-time apparent resistivity of the above two algorithms reflects the real situation of geoelectric model. The all-time apparent resistivity does not vary with the positions of measuring points. The first branch (early period) of all-time apparent resistivity is close to the first layer resistivity, and the end branch (late period) enlarges gradually and gets close to the third layer resistivity, which proves the correctness of the VFSA algorithm.

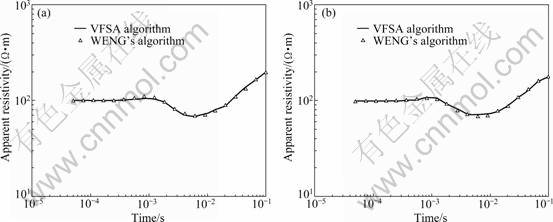
Fig.1 All-time apparent resistivities calculated utilizing VFSA and WENG’s algorithm: (a) Measuring point (20, -20); (b) Measuring point (260, -20)

With VFSA as a global optimization method, the all-time apparent resistivities obtained are global optimal solutions. However, the solutions calculated by dichotomy, which is a local optimization algorithm, may be local minima or maybe do not exist.

4.2 Three-layer geoelectric models

On the premise of verifying the correctness of algorithm of this work, the all-time apparent resistivities of some geoelectric models are calculated. The parameters are set as follows. The length and width of transmitting loop are 600 m and 400 m, respectively; the observing time series are 5 Hz time series of V8 multifunctional electrical prospecting apparatus; the origin of coordinate (0, 0) is in the center of rectangular loop; the positions of measuring points are (0, 0), (90, 60) and (180, 120). The parameters of three-layer geoelectric models are listed in Table 1. The VFSA parameters, terminal condition and scope selecting method of initial model are the same as the verification of algorithm.

Figure 2 shows the all-time apparent resistivities of three-layer geoelectric models calculated by VFSA. It can be seen that, every all-time apparent resistivity curve truly reflects the corresponding geoelectric model. The first branch of the curve (early period) gets close to the first layer resistivity, and the end branch of the curve (late period) gradually approaches to the third layer resistivity. As the algorithmic method of all-time apparent resistivity consists of the position information of measuring point, the tracing pattern is not affected by the position of measuring point. For the same model, the apparent resistivity of every measuring point slightly differs at some moments and the deviation is within 5%, which is caused by the terminal condition of VFSA. The current terminal condition is less than 1×10^-3 and it needs 5 min to calculate the all-time apparent resistivity at one moment. If the terminal condition is changed to be less than 1×10^-4 or smaller, it needs longer time to calculate.

Table 1 Parameters of three-layer geoelectric models

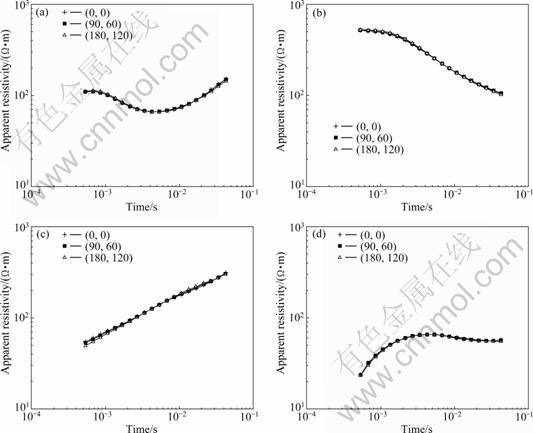
Fig.2 All-time apparent resistivities computed by VFSA: (a) Model 1; (b) Model 2; (c) Model 3; (d) Model 4

5 Conclusions

1) The all-time apparent resistivity of the measuring points in the rectangular transmitting loop of large loop TEM is obtained by utilizing VFSA to combine theoretical EMF and measured EMF. This algorithm consists of the position information of measuring point, thus the all-time apparent resistivity is not affected by the positions of measuring points and can truly reflect the geoelectric models, which provides technical guarantee for expanding the measuring area of the central area in the large loop and improving the outdoor work efficiency.

2) When utilizing the global optimizing VFSA to calculate the all-time apparent resistivity, it needs to conduct forward calculations repeatedly, so as to lower the computational efficiency. In order to achieve high efficient apparent resistivity, it must improve the forward calculation efficiency of the transient electromagnetic method.

References

[1] JIANG Bang-yuan. Applied near zone magnetic source transient electromagnetic exploration [M]. Beijing: Geological Press, 1998. (in Chinese)

[2] XIONG Bin. Inverse spline interpolation for the calculation of all-time resistivity for the larger-loop transient electromagnetic method [J]. Journal of Jilin University: Earth Science Edition, 2005, 35(4): 515-519. (in Chinese)

[3] LI Jian-ping, LI Tong-lin, ZHAO Xue-feng, LIANG Tai-mu. Study on the TEM all-time apparent resistivity of arbitrary shape loop source over the layered medium [J]. Progress in Geophysics, 2007, 22(6): 1777-1780. (in Chinese)

[4] WANG Hua-jun. Time domain transient electromagnetic all time apparent resistivity translation algorithm [J]. Chinese J Geophys, 2008, 51(6): 1936-1942. (in Chinese)

[5] ZHANG Cheng-fan, WENG Ai-hua, SUN Shi-dong, DONG Rui-chun. Computation of whole-time apparent resistivity of large rectangular loop [J]. Journal of Jilin University: Earth Science Edition, 2009, 39(4): 755-758. (in Chinese)

[6] WENG Ai-hua, LIU Yun-he, CHEN Yu-lin, DONG Rui-chun, LIAO Xiang-dong, JIA Ding-yu. Computation of transient electromagnetic field from a rectangular loop over stratified earths [J]. Chinese J Geophys, 2010, 53(3): 646-650.

[7] XI Zhen-zhu, LIU Jian, LONG Xia, HOU Hai-tao. Three-component measurement in transient electromagnetic method [J]. Journal of Central South University: Science and Technology, 2010, 41(1): 272-276. (in Chinese)

[8] FU Chang-min, DI Qing-yun, WANG Miao-yue. Calculate electromagnetic fields in stratified medium with layer-matrix [J]. Chinese J Geophys, 2010, 53(1): 177-188. (in Chinese)

[9] LI Jian-hui, LIU Shu-cai, ZHU Zi-qiang, LU Guang-yin, ZHAO Xiao-bo, ZHAO Shuang-qiu. Relationship between electromagnetic field and magnetic field’s symmetric excited by rectangular loop [J]. Journal of Central South University: Science and Technology, 2010, 41(2): 638-642. (in Chinese)

[10] NEWMAN G A, COMMER M. New advances in three dimensional transient electromagnetic inversion [J]. Geophys J Int, 2005, 160: 5-32.

[11] TANG Jing-tian, WANG Fei-yan, REN Zheng-yong, GUO Rong-wen. 3-D direct current resistivity forward modeling by adaptive multigrid finite element method [J]. Journal of Central South University of Technology, 2010, 17: 587-592.

[12] KAIKKONEN P, SHARMA S P. A comparison of performances of linearized and global nonlinear 2-D inversions of VLF and VLF-R electromagnetic data [J]. Geophysics, 2001, 66(3): 462–475.

[13] RYDEN N, PARK C B. Fast simulated annealing inversion of surface waves on pavement using phase-velocity spectra [J]. Geophysics, 2006, 71(4): R49-R58.

[14] MA X Q. Simultaneous inversion of prestack seismic data for rock properties using simulated annealing [J]. Geophysics, 2002, 67(6): 1877-1885.

[15] MISRAL S, SACCHI M D. Global optimization with model-space preconditioning application to AVO inversion [J]. Geophysics, 2008, 73(5): R71-R82.

[16] ROY L, SEN M K, DONALD D B, STOFFA P L, RICHTER T G. Inversion and uncertainty estimation of gravity data using simulated annealing: An application over Lake Vostok, East Antarctica [J]. Geophysics, 2005, 70(1): J1-J12.

[17] DAFFLON B, IRVING J, HOLLIGER K. Simulated-annealing- based conditional simulation for the local-scale characterization of heterogeneous aquifers [J]. Journal of Applied Geophysics, 2009, 68: 60-70.

[18] YIN C C, HODGES G. Simulated annealing for airborne EM inversion [J]. Geophysics, 2007, 72(4): F189-F195.

[19] KNIGHT J H, RAICHE A P. Transient electromagnetic calculations using the Gaver-Stehfest inverse laplace transform method [J]. Geophysics, 1982, 47(1): 47-50.

[20] EVERETT M E. Transient electromagnetic response of a loop source over a rough geological medium [J]. Geophys J Int, 2009, 177: 421-429.

[21] GUPTASARMA D, SINGH B. New digital linear filters for Hankel J₀ and J₁ transforms [J]. Geophysical Prospecting, 1997, 45: 745-762.

(Edited by YANG Bing)

Foundation item: Projects(40804027, 41074085) supported by the National Natural Science Foundation of China; Project(09JJ3048) supported by the Natural Science Foundation of Hunan Province, China; Project(200805331082) supported by the Research Fund for the Doctoral Program of Higher Education, China

Received date: 2010-07-07; Accepted date: 2010-08-31

Corresponding author: FENG De-shan, Associate Professor, PhD; Tel: +86-13618474853; E-mail: fengdeshan@126.com