A hybrid specific index-related process monitoring strategy based on a novel two-step information extraction method
来源期刊:中南大学学报(英文版)2018年第12期
论文作者:侍洪波 赵博 宋冰 谭帅
文章页码:2896 - 2909
Key words:specific index; hybrid monitoring strategy; two-step information extraction; subspace
Abstract: A two-step information extraction method is presented to capture the specific index-related information more accurately. In the first step, the overall process variables are separated into two sets based on Pearson correlation coefficient. One is process variables strongly related to the specific index and the other is process variables weakly related to the specific index. Through performing principal component analysis (PCA) on the two sets, the directions of latent variables have changed. In other words, the correlation between latent variables in the set with strong correlation and the specific index may become weaker. Meanwhile, the correlation between latent variables in the set with weak correlation and the specific index may be enhanced. In the second step, the two sets are further divided into a subset strongly related to the specific index and a subset weakly related to the specific index from the perspective of latent variables using Pearson correlation coefficient, respectively. Two subsets strongly related to the specific index form a new subspace related to the specific index. Then, a hybrid monitoring strategy based on predicted specific index using partial least squares (PLS) and T2 statistics-based method is proposed for specific index-related process monitoring using comprehensive information. Predicted specific index reflects real-time information for the specific index. T2 statistics are used to monitor specific index-related information. Finally, the proposed method is applied to Tennessee Eastman (TE). The results indicate the effectiveness of the proposed method.
Cite this article as: ZHAO Bo, SONG Bing, TAN Shuai, SHI Hong-bo. A hybrid specific index-related process monitoring strategy based on a novel two-step information extraction method [J]. Journal of Central South University, 2018, 25(12): 2896–2909. DOI: https://doi.org/10.1007/s11771-018-3961-y.

J. Cent. South Univ. (2018) 25: 2896-2909
DOI: https://doi.org/10.1007/s11771-018-3961-y

ZHAO Bo(赵博), SONG Bing(宋冰), TAN Shuai(谭帅), SHI Hong-bo(侍洪波)
Key Laboratory of Advanced Control and Optimization for Chemical Processes of Ministry of Education, East China University of Science and Technology, Shanghai 200237, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: A two-step information extraction method is presented to capture the specific index-related information more accurately. In the first step, the overall process variables are separated into two sets based on Pearson correlation coefficient. One is process variables strongly related to the specific index and the other is process variables weakly related to the specific index. Through performing principal component analysis (PCA) on the two sets, the directions of latent variables have changed. In other words, the correlation between latent variables in the set with strong correlation and the specific index may become weaker. Meanwhile, the correlation between latent variables in the set with weak correlation and the specific index may be enhanced. In the second step, the two sets are further divided into a subset strongly related to the specific index and a subset weakly related to the specific index from the perspective of latent variables using Pearson correlation coefficient, respectively. Two subsets strongly related to the specific index form a new subspace related to the specific index. Then, a hybrid monitoring strategy based on predicted specific index using partial least squares (PLS) and T2 statistics-based method is proposed for specific index-related process monitoring using comprehensive information. Predicted specific index reflects real-time information for the specific index. T2 statistics are used to monitor specific index-related information. Finally, the proposed method is applied to Tennessee Eastman (TE). The results indicate the effectiveness of the proposed method.
Key words: specific index; hybrid monitoring strategy; two-step information extraction; subspace
Cite this article as: ZHAO Bo, SONG Bing, TAN Shuai, SHI Hong-bo. A hybrid specific index-related process monitoring strategy based on a novel two-step information extraction method [J]. Journal of Central South University, 2018, 25(12): 2896–2909. DOI: https://doi.org/10.1007/s11771-018-3961-y.
1 Introduction
With the progress of science and technology, the scale of modern industrial process is becoming more and more complicated [1]. Production safety is the most basic requirement of modern industrial processes. On the basis of ensuring the safety of production, improving product quality is a necessary way to increase economic efficiency. Process monitoring ensures production safety and product quality, so much effort has been devoted to researching on process monitoring method [2–5]. Distributed control system (DCS) is widely used to gather massive process data. Pattern recognition and data mining create the conditions for data analysis. Therefore, the data-driven process monitoring methods have yielded remarkable achievements [6–8].
The specific index is the most concerned index in the process, such as product quality, economic costs and so on. As the research progresses, some scholars have found that not all faults affect specific index. Traditional process monitoring methods like principal component analysis (PCA) cannot distinguish whether a fault affects specific index, which leads to unnecessary downtime and maintenance. Therefore, specific index-related process monitoring methods should aim to classify the faults more targeted [9–13]. The essential difference between them is whether they are supervised methods. At present, it is still a challenge to distinguish between the specific index-related information and the specific index-unrelated information.
Up to now, specific index-related process monitoring methods are divided into three categories: direct decomposition methods, linear regression-based methods, and PLS-based methods [14, 15]. The direct decomposition methods perform a singular value decomposition (SVD) on the cross-covariance matrix between process variables and the specific index. The linear regression-based methods mainly include least squares (LS) regression-based method and principal component regression (PCR)-based method. LS regression-based method predicts the specific index not only according to the cross-covariance between process variables and the specific index but also the covariance of the specific index [16]. Similar to LS regression-based method [12], the PCR-based method was presented for specific index-related process monitoring by DING et al [17]. The PLS-based methods consist of original PLS-based method and some improved PLS-based methods [18–20]. One step of the three categories of methods is to obtain specific index-related subspaces and specific index-unrelated subspaces.
With the advancement of the research, scholars found that there are still some defects. On the one hand, the specific index-related subspace contains useless ingredients, which are orthogonal to the specific index. On the other hand, the specific index-unrelated subspace still contains some information related to the specific index. For example, the principal component space of PLS reflects the change relate to the specific index, but it contains some information unrelated to the specific index. Residuals may still be very large, since PLS do not extract principal components in the order of variances. In order to overcome the shortcomings of PLS, the improved PLS methods were presented. The total PLS (TPLS) is the further decomposition of PLS, considering the information unrelated to the specific index in principal component space and the important change information in residual space [19, 21, 22]. Concurrent PLS (CPLS) attempts to break down subspaces more accurately and detailedly [20, 23]. Five latent structures, i.e., process subspace unrelated to the specific index, specific index subspace unrelated to process, process-specific index covariation subspace, potentially process- related subspace, and potentially specific index- related subspace, are built by CPLS. Although the decomposition of TPLS and CPLS is accurately and detailedly, a large number of subspaces lead to explanation difficulty and monitor cumbersomely. As the research promotes, some scholars are not satisfied with only focusing on post-processing technology. A process monitoring strategy based on multispace T-PLS (MsT-PLS) was developed [24]. The process variables can be separated according to their different types, sources or operation units. Then, the TPLS is performed on each variable subspace. Thereafter, a linearity evaluation and variable subset partition based hierarchical process modeling and monitoring method was proposed [25]. Linear subsets and nonlinear subset are identified based on the iterative evaluation of variable correlations. In the lower level, PCA explores linear correlations encapsulated in each linear subset and KPCA as upper level model captures process nonlinearity. Inspired by this, the method proposed in this paper divides the process variables into two subspaces according to the quality-related degree, aiming at a clearer separation of process variables.
The soft sensing-based method picks out the easy-to-measure variables to represent the key variables that are difficult to measure or are temporarily unable to measure [26]. It only focuses on predicted specific index. When a fault occurs on process variables, the specific index is not affected by the fault immediately. Predicted specific index still does not exceed the control limit at the beginning of the fault duration. As well-known, the feedback mechanism is present in the realistic industrial process to guarantee stability of running state after a fault occurring. It may cause some process variables to stabilize at a new steady-state value. Sometimes, the traditional T2 statistics-based method still warns when the fault is adjusted by feedback. In summary, the soft sensing-based method and the traditional T2 statistics-based method have their own shortcomings. Therefore, a hybrid specific index-related process monitoring strategy is necessary to present.
In this paper, a hybrid specific index-related process monitoring strategy based on a novel two-step information extraction method (T-SIEM) is proposed. Firstly, perform the two-step information extraction method on process variables to feature the specific index-related information. In the first step, overall process variables are separated into two sets based on Pearson correlation coefficient, where the two sets comprise the process variables strongly and weakly related to the specific index, respectively. Performing PCA on the two sets, the directions of latent variables are different from the directions of process variables. In other words, the correlation between latent variables in the set with strong correlation and the specific index may weaken. The correlation between latent variables in the set with weak correlation and the specific index may strengthen. In the second step, the two sets are further divided into a subset strongly related to the specific index and a subset weakly related to the specific index from the perspective of latent variables using Pearson correlation coefficient, respectively. Two subsets strongly related to specific index form a new subspace related to the specific index. Different from the soft sensing- based method and the traditional T2 statistics-based method, a novel hybrid monitoring strategy is presented in this paper. The prediction model of the specific index based on PLS and T2 statistics using extracted information are established, respectively. By comparing and analyzing, a more accurate, more detailed monitoring result is captured than the soft sensing-based method and the traditional T2 statistics-based method. The contributions of this paper are listed as follows: 1) A novel two-step information extraction method is proposed to extract the information related to the specific index. 2) A hybrid monitoring strategy is presented to capture monitoring results more accurately and detailedly.
The structure of this paper is designed as follows. Section 2 introduces PCA and PLS briefly. A hybrid specific index-related process monitoring strategy using a novel two-step information extraction method is presented in Section 3. In Section 4, the proposed method is applied to TE chemical process. The article is concluded in Section 5.
2 Preliminaries
2.1 Principal component analysis (PCA)
PCA is one of the most basic projection models in multivariate statistical analysis methods [27–29]. Construct a measurement data matrix  where m is the number of sensors, and every sensor has n independent samples. Every column in X represents a measurement variable, and every row in X represents a measurement sample. After mean- centering and variance-scaling, the covariance matrix of X is given as:
where m is the number of sensors, and every sensor has n independent samples. Every column in X represents a measurement variable, and every row in X represents a measurement sample. After mean- centering and variance-scaling, the covariance matrix of X is given as:
 (1)
(1)
Performing a SVD on the covariance matrix S gives:
 (2)
(2)
where is the singular values sorted in descending order. S is the singular vectors corresponding to the singular values. The process variables X is decomposed by PCA as:
is the singular values sorted in descending order. S is the singular vectors corresponding to the singular values. The process variables X is decomposed by PCA as:
 (3)
(3)
where  is the projection matrix,
is the projection matrix,  is the score matrix.
is the score matrix.
2.2 Partial least squares (PLS) regression methods
PLS is an effective soft-sensing modeling method. Process variables 
 and the specific index
and the specific index are related by PLS via the score matrix T. The score matrix T has a reduced dimension, but it captures most related information between process variables X and the specific index Y. Based on a common notation, X and Y can be decomposed by PLS as:
are related by PLS via the score matrix T. The score matrix T has a reduced dimension, but it captures most related information between process variables X and the specific index Y. Based on a common notation, X and Y can be decomposed by PLS as:
 (4)
(4)
where 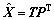 and
and 
 is the score matrix,
is the score matrix, is the loading matrix of X,
is the loading matrix of X,  is the he loading matrix of Y, A is the number of principle component based on PLS, E and F are the modeling errors of X and Y, respectively.
is the he loading matrix of Y, A is the number of principle component based on PLS, E and F are the modeling errors of X and Y, respectively.  is given from X:
is given from X:
 (5)
(5)
where ri is given from weight vectors:
 (6)
(6)
where wi is the ith weight vector. The score matrix T is calculated as:
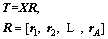 (7)
(7)
the relationship of P, R and W is formulated as:
 (8)
(8)
The X can be decomposed with supervision by Y using PLS as:
 (9)
(9)
3 Framework of novel monitoring strategy
3.1 Novel two-step information extraction method (T-SIEM)
3.1.1 First step: information extraction from process variables
The process variables 
 and the specific index
and the specific index  are captured offline, where n is the number of samples, and m is the number of process variables. Perform mean- centering and variance-scaling on X and Y. The correlation between two variables can be measured with many statistical values. The most common correlation coefficient is Pearson correlation coefficient, which reflects the degree of correlation between two variables. The mathematical expression of the Pearson correlation coefficient is described as:
are captured offline, where n is the number of samples, and m is the number of process variables. Perform mean- centering and variance-scaling on X and Y. The correlation between two variables can be measured with many statistical values. The most common correlation coefficient is Pearson correlation coefficient, which reflects the degree of correlation between two variables. The mathematical expression of the Pearson correlation coefficient is described as:


 (10)
(10)
where r is Pearson correlation coefficient, Xi and Yi are the measured values of X and Y,  and
and  are the average values of X and Y, σX and σY are the standard deviation of X and Y, and n is the number of samples. The values of r are between [–1, 1]. The greater the absolute value of r is, the stronger the correlation between two variables.
are the average values of X and Y, σX and σY are the standard deviation of X and Y, and n is the number of samples. The values of r are between [–1, 1]. The greater the absolute value of r is, the stronger the correlation between two variables.
The correlation between each process variable xi (i=1, 2, …, m) and the specific index Y is given according to Eq. (10):
 (11)
(11)
The absolute values of ri are sorted in descending order. The correlation between X and Y is formulated as:
 (12)
(12)
The accumulating correlation coefficient contribution method is presented to capture process variables strongly and weakly related to specific index. It is described as:
 (13)
(13)
As a consequence, the correlation between X and Y is divided as:
 (14)
(14)
where rs consists of A large absolute values of ri, rw consists of m–A the small absolute values of ri. The process variables X are separated as:
 (15)
(15)
where  is the process variables strongly related to the specific index corresponding to rs.
is the process variables strongly related to the specific index corresponding to rs.  is the process variables weakly related to the specific index corresponding to rw.
is the process variables weakly related to the specific index corresponding to rw.
In the first step, process variables are roughly separated into two subsets: Xs and Xw. Xs is strongly related to the specific index, Xw is weakly related to the specific index. However, Xs still contains some information orthogonal to the specific index and Xw consists of some information related to the specific index.
3.1.2 Second step: information extraction from latent variables
In the first step, process variables X are divided into Xs and Xw. Then, performing PCA on Xs and Xw, latent variables are given as:
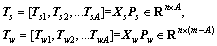 (16)
(16)
where Ps and Pw are the projection matrixes of Xs and Xw, respectively. The principal components extracted by PCA can well summarize the information in process variables, but often lack the ability to explain the specific index. In other words, after the PCA-based projection, some of the latent variables in Xs become weakly related to the specific index, and some of the latent variables in Xw become strongly related to the specific index. The theory is proved from the mathematical viewpoint as follows.
Process variables and the specific index are given as:
 (17)
(17)
where n is the number of samples, and m is the number of process variables. For easy calculation, perform mean-centering and variance-scaling on X and Y. The correlation between xi (i=1, 2, …, m) and Y is given as:
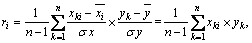
 (18)
(18)
Latent variables are calculated based on PCA as:

 (19)
(19)
where i=1, 2, …, m. The correlation between Ti (i=1, 2, …, m) and Y is given as:
i=1, 2, …, m. The correlation between Ti (i=1, 2, …, m) and Y is given as:

 (20)
(20)
Bring Eq. (18) into Eq. (20):
 i=1, 2, …, m (21)
i=1, 2, …, m (21)
As can be seen from Eq. (21), Ri is a linear combination of ri. Large ri may get small Ri, similarly, small ri may obtain large Ri. In other words, although process variables in Xs are strongly related to Y, some latent variables may weakly related to Y. Similarly, process variables in Xw are weakly related to Y, some latent variables may strongly related to Y. In summary, it is necessary to further extract specific index-related information in the second step.
In the Xs-subset, the correlation between each latent variable Tsi (i=1, 2, …, A) and the specific index Y is calculated according to Eq. (21):
 i=1, 2, …, A (22)
i=1, 2, …, A (22)
The absolute values of Rsi are sorted in descending order. The correlation between Tsi and Y is formulated as:
 (23)
(23)
Latent variables are divided into strongly and weakly related to the specific index via the accumulating correlation coefficient contribution method. It is described as:
 (24)
(24)
As a result, the correlation between Ts and Y is divided as:
 (25)
(25)
where Rss consists of As large absolute values in Rs, Rsw consists of A–As the small absolute values in Rs. The latent variables Ts are separated as:
 (26)
(26)
where  is the process variables strongly related to the specific index corresponding to Rss.
is the process variables strongly related to the specific index corresponding to Rss.  is the process variables weakly related to the specific index corresponding to Rsw.
is the process variables weakly related to the specific index corresponding to Rsw.
In the Xw-subset, the correlation between each latent variable Twi (i=1, 2, …, m–A ) and the specific index Y is calculated according to Eq. (21):

i=1, 2, …, m–A (27)
The absolute values of Rwi are sorted in descending order. The correlation between Twi and Y is formulated as:
 (28)
(28)
Latent variables are divided into strongly and weakly related to the specific index via the accumulating correlation coefficient contribution method. It is described as:
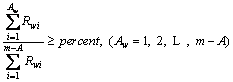 (29)
(29)
As a result, the correlation between Tw and Y is divided as:
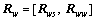 (30)
(30)
where Rws consists of Aw large absolute values in Rw, Rsw consists of m–A–Aw small absolute values in Rw. The latent variables Tw are separated as:
 (31)
(31)
where  is latent variables strongly related to the specific index corresponding to Rws.
is latent variables strongly related to the specific index corresponding to Rws.  is latent variables weakly related to the specific index corresponding to Rww.
is latent variables weakly related to the specific index corresponding to Rww.
Construct two subspaces: Trel and Tunrel.
 (32)
(32)
where Trel is a subspace related to the specific index Y, and Tunrel is a subspace unrelated to the specific index Y.
3.2 Hybrid specific index-related process monitoring strategy
3.2.1 Prediction model based on PLS
Trel and Y are related by PLS.
 (33)
(33)
where is the score matrix,
is the score matrix,  is the loading matrix of X,
is the loading matrix of X,  is the loading matrix of Y, k is the number of principle component based on PLS, E and F are the modeling residual errors of X and Y, respectively.
is the loading matrix of Y, k is the number of principle component based on PLS, E and F are the modeling residual errors of X and Y, respectively.
The predicted values of Y are calculated according to Eqs. (4)–(9):
 (34)
(34)
The upper control limit and lower control limit are estimated by kernel density estimation.
3.2.2 T2 statistics-based monitoring method
T2 statistics in Trel-subspace can be given as:
 (35)
(35)
where 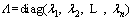 is the variance of Trel. The control limit is estimated via Eq. (36).
is the variance of Trel. The control limit is estimated via Eq. (36).
 (36)
(36)
3.2.3 Decision logic
The prediction model only focuses on predicted specific index. When a fault occurs on process variables, specific index is not affected by the fault immediately. Predicted specific index is still not exceed the control limit at the beginning of the fault duration. Based on a common notation, the feedback mechanism is present in the realistic industrial process to guarantee stability of running state after a fault occurring. It may cause some process variables to smooth at a new steady-state value. The T2 statistics-based method still warns when the fault is adjusted by feedback, sometimes.
In order to make above two types of methods complementary, a hybrid monitoring strategy is presented. The decision logic is as follows:

Eventually, the novel specific index-related process monitoring strategy using a novel two-step information extraction method can be concluded in Figure 1.
3.3 Discussion about hybrid monitoring strategy using two-step information extraction method
Two-step information extraction method captures related information very well. It divides process variables into two sets strongly and weakly related to the specific index in the first step, which makes some information unrelated to specific index remove from the source. In the second step, the specific index-related information is further captured via selecting the latent variables, which removes some unrelated information further and compensates some related information. As a consequence, the information extracted by two-step information extraction method consists of more related information than other methods.
The hybrid monitoring strategy is integrated by a prediction model based on PLS and T2 statistics-based monitoring method. At the beginning of a fault occurring on process variables, the impact of the fault does not immediately affect the specific index. As a result, the predicted specific index will not exceed the control limit within a certain period of time. At this point, T2 statistics-based monitoring method will warn in a timely manner. With the occurrence of the fault, the fault may be adjusted by feedback, which may cause some process variables smooth at a new stead-state value. Sometimes, the T2 statistics-based method still warns when the fault is adjusted by feedback. At this point, predicted specific index fall back to the control limits. The hybrid monitoring strategy provides a more reasonable monitoring result under the simple analysis of the operators.
4 Case studies
4.1 Description of TE
TE is a simulation of a realistic industrial process. The whole process consists of five operating units: reactor, condenser, liquid separator, recycle compressor, and a product stripper [30, 31]. The chemical reactions in TE process are as follows:
 (37)
(37)
where A, C, D and E are reactants, G and H are products, B is inert gas, and F is a by-product.
As a complex chemical process, a total of 53 variables are available, where there are 41 measurement variables and 11 manipulated variables [32–35]. The measurement variables consist of 22 continuous variables and 19 component variables [36, 37]. In addition, 21 faults are designed for process monitoring, where the reasons of 15 faults are known.
4.2 Benchmark simulation
The effectiveness of the hybrid specific index-related process monitoring strategy using two-step information extraction method was demonstrated on the TE process in this section. 22 continuous variables of measurement variables (XMEAS(1-22)) and 11 manipulated variables (XMV(1-11)) were combined into 33 process variables. The composition G (XMEAS(35)) in stream 9 was taken as specific index. The training data set consisted of 960 samples. Every testing data set included 160 normal samples and 800 fault samples. Faults 1, 2, 5, 6, 7, 8, 12, 13 are specific index-related faults and faults 3, 4, 9, 10, 11, 14, 15 are specific index-unrelated faults [36]. In addition, specific index-related faults are further divided into faults with feedback adjustment (faults 1, 5, 7) and faults without feedback adjustment (faults 2, 6, 8, 12, 13).
In order to verify that the correlation based on two-step information extraction method is stronger than the one based on selecting latent variables directly, the angles between specific index-related subspace and the specific index were calculated, respectively. The result shows that the angle of the proposed method is 11.16° lower than the one of selecting the latent variables directly. It is observed that the proposed method capture stronger correlation in specific index-related subspace than the method selecting the latent variables directly.

Figure 1 Framework of a novel monitoring strategy
4.3 Results and analysis
The monitoring results for TE based on PLS-based method, TPLS-based method and hybrid monitoring strategy method are listed in Table 1.
The results show that the hybrid monitoring strategy achieves the best monitoring performance for most faults. Monitoring performance is analyzed in detail according to the classification of faults.
Table 1 Detection rates of PLS-based method, TPLS-based method and hybrid monitoring strategy method

4.3.1 Specific index-related faults with feedback adjustment
Based on a common notation, faults 1, 5, 7 are the specific index-related faults with feedback adjustment. Fault 1 is a step fault that occurs at the 161st sampling point. At about the 450th sampling point, the specific index is adjusted to the normal range by feedback. Taking fault 1 as an example, perform PLS-based method, TPLS-based method and hybrid monitoring strategy method on the TE process for comparison purpose. The results of PLS-based method and TPLS-based method for fault 1 are shown in Figure 2. The specific index affected by fault 1 and the results of the hybrid monitoring strategy are demonstrated in Figure 3.
In Figures 2 and 3, it is observed that the fault occurs at the 161st sampling point and ends at about 450th sampling point. In the early stages of the fault, PLS and TPLS can timely alarm. As the fault is adjusted to the normal state by feedback, PLS and TPLS still issue an alarm and do not return to normal. For hybrid monitoring strategy, the specific index is not immediately affected by the fault, so predicted specific index will not exceed the control limit at the beginning of the fault. However, the method based on T2 statistic immediately responds in the early fault. In this case, it means that a specific index-related fault may occur soon. Operators should be guarded as early as possible. When the fault is adjusted to the normal state by feedback, predicted specific index changes from fault to normal. However, the feedback adjustment may cause some process variables to smooth at a new steady-state value, which makes the method based on T2 statistic still issue an alarm. In this case, it means that the fault is adjusted to the normal by feedback, but the system runs in a non-optimal state. In Figure 4, the specific index and some process variables strongly related to the specific index are listed to illustrate the above situation, the monitoring results are consistent with the actual situation.

Figure 2 Results of PLS-based method and TPLS-based method for fault 1
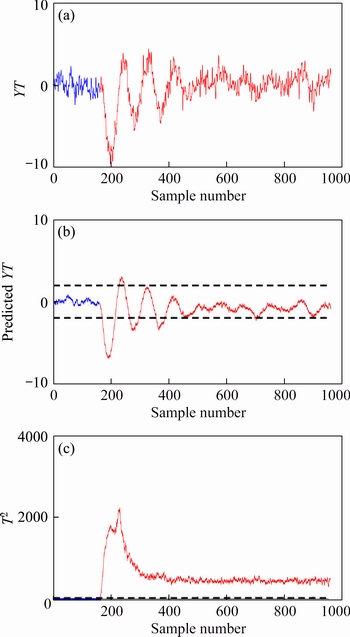
Figure 3 Results of hybrid monitoring strategy method for fault 1
4.3.2 Specific index-related faults without feedback adjustment
This type of faults will always exist once they occur, without adjusting themselves to the normal state, such as fault 8. Fault 8 is an increase in the variability of some process variables occurring at the 161st sampling point. Perform PLS-based method, TPLS-based method and hybrid monitoring strategy method on the TE process for comparison purpose. The results of PLS-based method and TPLS-based method for fault 8 are shown in Figure 5. The specific index affected by fault 8 and the results of the hybrid monitoring strategy are demonstrated in Figure 6.

Figure 4 Specific index and some process variables under fault 1 conditions
In Figures 5 and 6, the fault starts at the 161st sampling, causing specific index to intensify. PLS can get very good monitoring results in T2-space. TPLS obtain not very good monitoring results in both and Or-subspace. For hybrid monitoring strategy, predicted specific index can well follow the change of the real specific index, and the detection rate of T2 statistic-based method gets up to about 97.875%. It is worth mentioning that process monitoring based on predicted specific index needs to be observed over a period of time.
and Or-subspace. For hybrid monitoring strategy, predicted specific index can well follow the change of the real specific index, and the detection rate of T2 statistic-based method gets up to about 97.875%. It is worth mentioning that process monitoring based on predicted specific index needs to be observed over a period of time.

Figure 5 Results of PLS-based method and TPLS-based method for fault 8

Figure 6 Results of hybrid monitoring strategy method for fault 8
4.3.3 Specific index-unrelated faults
The occurrence of such faults does not cause changes in specific index, like fault 11. Fault 11 is an increase in the variability of some process variables occurring at the 161st sampling point. Perform PLS-based method, TPLS-based method and hybrid monitoring strategy method on the TE process for comparison purpose. The results of PLS-based method and TPLS-based method for fault 11 are shown in Figure 7. The specific index affected by fault 11 and the results of the hybrid monitoring strategy are demonstrated in Figure 8.

Figure 7 Results of PLS-based method and TPLS-based method for fault 11
In Figures 7 and 8, it is observed that the fault unrelated to specific index. PLS still has a high fault detection rate in T2-space. TPLS has a high fault detection rate in Qr-space, although the fault detection rate in  -space is low. For hybrid monitoring strategy, predicted specific index and T2 statistic-based method do not exceed the control limit. It has the best monitoring performance.
-space is low. For hybrid monitoring strategy, predicted specific index and T2 statistic-based method do not exceed the control limit. It has the best monitoring performance.
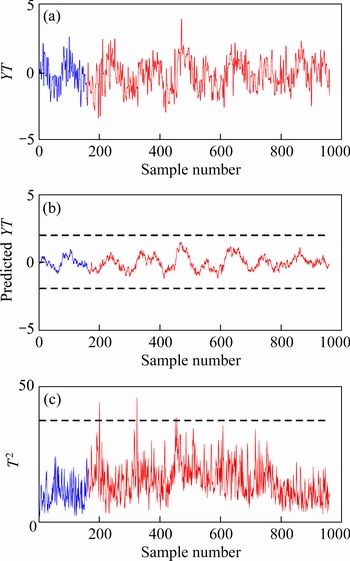
Figure 8 Results of hybrid monitoring strategy method for fault 11
Obviously, two-step information extraction method removes most information unrelated to specific index.
In summary, the novel hybrid process monitoring strategy using two-step information extraction method has the best monitoring performance and the clearest explanation for specific index-related faults with or without feedback adjustment, and specific index-unrelated faults. Two-step information extraction method removes most information unrelated to specific index, which provide support for the hybrid monitoring strategy. The hybrid monitoring strategy provides a more comprehensive and clearer explanation for process monitoring.
5 Conclusions
In this paper, a novel hybrid process monitoring strategy using two-step information extraction method is presented for specific index-related process monitoring. Firstly, the two-step information extraction method is performed on process variables to feature specific index-related information. In the first step, overall process variables are separated into two sets based on Pearson correlation coefficient, where the two sets comprise the process variables strongly and weakly related to the specific index, respectively. Through performing PCA on the two sets, the directions of latent variables are different from the directions of process variables. In the second step, performing PCA on the two sets, the two sets are further divided into a subset strongly related to specific index and a subset weakly related to specific index from the perspective of latent variables using Pearson correlation coefficient, respectively. Two subsets strongly related to the specific index form a new subspace related to the specific index. In addition, this paper presents a novel hybrid monitoring strategy. The prediction model of specific index based on PLS and T2 statistics using extracted information are established, respectively. By comparing and analyzing, a more accurate, and more detailed monitoring result is captured than the soft sensing-based method and the traditional T2 statistics-based method. Two-step information extraction method captures most related information, which provides support for the hybrid monitoring strategy. The hybrid monitoring strategy provides a more comprehensive and clearer explanation for process monitoring. Finally, the superior process monitoring performance of the proposed method is verified by TE process.
References
[1] SONG Bing, TAN Shuai, SHI Hong-bo. Key principal components with recursive local outlier factor for multimode chemical process monitoring [J]. Journal of Process Control, 2016, 47: 136–149.
[2] MOUSAVI H, SHAHBAZIAN M, JAZAYERI-RAD H, NEKOUNAM A. Reconstruction based approach to sensor fault diagnosis using auto-associative neural networks [J]. Journal of Central south University, 2014, 21: 2273–2281.
[3] WANG Fu-li, TAN Shuai, PENG Jun, CHANG Yu-qing. Process monitoring based on mode identification for multi-mode process with transitions [J]. Chemometrics & Intelligent Laboratory Systems, 2012, 110: 144–155.
[4] WANG Bei, YAN Xue-feng, JIANG Qing-chao. Independent component analysis model utilizing de-mixing information for improved non-Gaussian process monitoring [J]. Computers & Industrial Engineering, 2016, 94: 188–200.
[5] LV Zhao-min, YAN Xue-feng. Hierarchical support vector data description for batch process monitoring [J]. Industrial & Engineering Chemistry Research, 2016, 55: 9205–9214.
[6] AJAMI A, DANESHVAR M. Independent component analysis approach for fault diagnosis of condenser system in thermal power plant [J]. Journal of Central south University, 2014, 21: 242–251.
[7] ZHAO Chun-hui, GAO Fu-rong. A sparse dissimilarity analysis algorithm for incipient fault isolation with no priori fault information [J]. Control Engineering Practice, 2017, 65: 70–82.
[8] SONG Bing, MA Yu-xin, SHI Hong-bo. Multimode process monitoring using improved dynamic neighborhood preserving embedding [J]. Chemometrics & Intelligent Laboratory Systems, 2014, 135: 17–30.
[9] LI Gang, LIU Bao-sheng, QIN S J, ZHOU Dong-hua. Quality relevant data-driven modeling and monitoring of multivariate dynamic processes: The dynamic T-PLS approach [J]. IEEE Transactions on Neural Networks, 2011, 22: 2262–2271.
[10] QIN S J, ZHANG Ying-wei. Quality-relevant and process-relevant fault monitoring with concurrent projection to latent structures [J]. AIChE Journal, 2013, 59: 496–504.
[11] JIA Qi-long, ZHANG Ying-wei. Quality-related fault detection approach based on dynamic kernel partial least squares [J]. Chemical Engineering Research & Design, 2016, 106: 242–252.
[12] JIAO Jian-fang, YU Han, WANG Guang. A quality-related fault detection approach based on dynamic least squares for process monitoring [J]. IEEE Transactions on Industrial Electronics, 2016, 63: 2625–2632.
[13] GE Zhi-qiang, CHEN Xin-ru. Supervised linear dynamic system model for quality related fault detection in dynamic processes [J]. Journal of Process Control, 2016, 44: 224–235.
[14] ZHANG Kai, HAO Hai-yang, CHEN Zhi-wen, DING S X, DING E L. Comparison study of multivariate statistics based key performance indicator monitoring approaches [J]. IFAC Proceedings Volumes, 2014, 47(3): 10628–10633.
[15] ZHANG Kai, HAO Hai-yang, CHEN Zhi-wen, DING S X, PENG Kai-xiang. A comparison and evaluation of key performance indicator-based multivariate statistics process monitoring approaches [J]. Journal of Process Control, 2015, 33: 112–126.
[16] QIN S J. Recursive PLS algorithms for adaptive data modeling [J]. Computers & Chemical Engineering, 1998, 22: 503–514.
[17] DING S X, YIN Shen, PENG Kai-xiang, SHEN Bo. A novel scheme for key performance indicator prediction and diagnosis with application to an industrial hot strip mill [J]. IEEE Transactions on Industrial Informatics, 2013, 9: 2239–2247.
[18] PENG Kai-xiang, ZHANG Kai, YOU Bo, DONG Jie. Quality-related prediction and monitoring of multi-mode processes using multiple PLS with application to an industrial hot strip mill [J]. Neurocomputing, 2015, 168: 1093–1103.
[19] DONG Jie, ZHANG Kai, Huang Ya, PENG Kai-xiang. Adaptive total PLS based quality-relevant process monitoring with application to the Tennessee Eastman process [J]. Neurocomputing, 2015, 154: 77–85.
[20] LIU Qiang, QIN S J, CHAI Tian-you. Quality-relevant monitoring and diagnosis with dynamic concurrent projection to latent structures [J]. IFAC Proceedings Volumes, 2014, 47(3): 2740–2745.
[21] ZHOU Dong-hua, LI Gang, QIN S J. Total projection to latent structures for process monitoring [J]. AIChE Journal, 2010, 56: 168–178.
[22] LI Gang, LIU Bao-sheng, QIN S J, ZHOU Dong-hua. Quality relevant data-driven modeling and monitoring of multivariate dynamic processes: the dynamic T-PLS approach [J]. IEEE Transactions on Neural Networks, 2011, 22: 2262–2271.
[23] ZHANG Ying-wei, SUN Rong-rong, FAN Yun-peng. Fault diagnosis of nonlinear process based on KCPLS reconstruction [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 140: 49–60.
[24] ZHAO Chun-hui, SUN You-xian. Multispace total projection to latent structures and its application to online process monitoring [J]. IEEE Transactions on Control Systems Technology, 2014, 22: 868–883.
[25] LI Wen-qing, ZHAO Chun-hui. Linearity evaluation and variable subset partition based hierarchical monitoring strategy for processes with hybrid variable correlations [J]. IEEE Transactions on Industrial Electronics, 2018, 3: 2683–2691.
[26] JU Hao, YIN Shen, GAO Hui-jun. KAYNAK O. A data-based KPI prediction approach for wastewater treatment processes [C]// International Conference on Man and Machine Interfacing. IEEE, 2015: 1–6.
[27] LV Zhao-min, YAN Xue-feng, JIANG Qing-chao. Batch process monitoring based on multiple-phase online sorting principal component analysis [J]. ISA Transactions, 2016, 64: 342–352.
[28] WANG Xiao-gang, HUANG Li-wei, ZHANG Ying-wei. Modeling and monitoring of nonlinear multi-mode processes based on similarity measure-KPCA [J]. Journal of Central South University, 2017, 24: 665–674.
[29] TONG Chu-dong, LAN Ting, SHI Xu-hua. Fault detection and diagnosis of dynamic processes using weighted dynamic decentralized PCA approach [J]. Chemometrics & Intelligent Laboratory Systems, 2017, 161: 34–42.
[30] DOWNS J J, VOGEL E F. A plant-wide industrial process control problem [J] Computers & Chemical Engineering, 1993, 17: 245–255.
[31] MCAVOY T J, YE N. Base control for the Tennessee Eastman problem [J]. Computers & Chemical Engineering, 1994, 18(5): 383–413.
[32] WANG Fan, ZHU Hong-lin, TAN Shuai, SHI Hong-bo. Orthogonal nonnegative matrix factorization based local hidden Markov model for multimode process monitoring [J]. Chinese Journal of Chemical Engineering, 2016, 24: 856–860.
[33] SONG Bing, TAN Shuai, SHI Hong-bo. Process monitoring via enhanced neighborhood preserving embedding [J]. Control Engineering Practice, 2016, 50: 48–56.
[34] ZHAO Chun-hui, GAO Fu-rong. A nested-loop Fisher discriminant analysis algorithm [J]. Chemometrics and Intelligent Laboratory Systems, 2015, 146: 396–406.
[35] SONG Bing, SHI Hong-bo. Temporal-spatial global locality projections for multimode process monitoring [J]. IEEE Access, 2018, 6: 2169–3536.
[36] ZHAO Fu-zhou, SONG Bing, SHI Hong-bo. Multi-mode process monitoring based on a novel weighted local standardization strategy and support vector data description [J]. Journal of Central south University, 2016, 23: 2896–2905.
[37] ZHAO Chun-hui, WANG Wei, QIN Yan, GAO Fu-rong. Comprehensive subspace decomposition with analysis of between-mode relative changes for multimode process monitoring [J]. Industrial & Engineering Chemistry Research, 2015, 54: 3154–3166.
[38] WANG Guang, YIN Shen. Quality-related fault detection approach based on orthogonal signal correction and modified PLS [J]. IEEE Transactions on Industrial Informatics, 2015, 11(2): 398–405.
(Edited by HE Yun-bin)
中文导读
基于一种新的两步信息提取方法的混合过程监测策略研究
摘要:提出一个两步信息提取方法用于更精确地捕获性能指标相关的信息。在第一步中,根据皮尔森相关系数,所有的过程变量被分成两个集合。其中一个由与特定指标强相关的过程变量组成,另一个集合由特定指标弱相关过程变量组成。随后,在两个集合中执行PCA分解,潜变量的方向不同于原始的过程变量。也就是说,原本强相关变量集合中的潜变量与特定指标的相关性可能会变弱。然而,弱相关变量集合中的潜变量与特定指标的相关性可能会变强。因此,在第二步中,根据皮尔森相关系数,两个集合被进一步从潜变量的角度分解为四个子集。得到的两个与特定指标强相关的子集构成与特定指标相关的子空间。接着,一种基于T2统计量和预测的特定指标的混合监控策略被提出用于特定指标相关的过程监测。最后,提出的方法被应用于TE过程,结果显示了所提方法的有效性。
关键词:特定指标;混合监控策略;两步信息提取;子空间
Foundation item: Projects(61374140, 61673173) supported by the National Natural Science Foundation of China;Projects(222201717006, 222201714031) supported by the Fundamental Research Funds for the Central Universities, China
Received date: 2017-08-19; Accepted date: 2018-03-30
Corresponding author: SHI Hong-bo, PhD, Professor; Tel: +86-21-64252189; E-mail: hbshi@ecust.edu.cn; ORCID: 0000-0001-9400- 1415

