Trans. Nonferrous Met. Soc. China 22(2012) 447-455

Thermodynamic model for equilibrium solubility of gibbsite in concentrated NaOH solutions

LI Xiao-bin, YAN Li, ZHOU Qiu-sheng, LIU Gui-hua, PENG Zhi-hong

School of Metallurgical Science and Engineering, Central South University, Changsha 410083, China

Received 4 March 2011; accepted 12 June 2011

Abstract: The thermodynamic properties of the most important NaOH-NaAl(OH)₄-H₂O system in Bayer process for alumina production were investigated. A theoretical model for calculating the equilibrium constant of gibbsite dissolved in sodium hydroxide solution was proposed. New Pitzer model parameters and mixing parameters for the system NaOH-NaAl(OH)₄-H₂O were yielded and tested in the temperature range of 298.15-373.15 K. The results show that the proposed model for calculating the equilibrium constant of gibbsite dissolution is applicable and accurate. The obtained Pitzer model parameters of β⁽⁰⁾(NaAl(OH)₄), β⁽¹⁾(NaAl(OH)₄), C^Φ(NaAl(OH)₄) for NaAl(OH)₄, the binary mixing parameter of θ(OH^-Al(OH)₄^-) for Al(OH)₄^- with OH^-, and the ternary mixing parameter of ψ(Na⁺OH^-Al(OH)₄^-) for Al(OH)₄^- with OH^- and Na⁺ are temperature-dependent. The prediction of the equilibrium solubility of gibbsite dissolved in sodium hydroxide solution was feasible in the temperature range of 298.15-373.15 K.

Key words: Pitzer model; sodium aluminate solution; gibbsite; equilibrium constant; equilibrium solubility

1 Introduction

The solubility isotherm of the Na₂O-Al₂O₃-H₂O system at different temperatures is the research foundation of the Bayer alumina production and phase equilibrium, which plays an important role in the industry of alumina production. The essence of the Bayer process is that alumina hydrates dissolve and precipitate alternately in the Na₂O-Al₂O₃-H₂O system under different conditions. Unfortunately, notably conflicting objectives between product quality and yield in precipitation require a solution. The focus of this study, therefore, is on the equilibrium solubility of gibbsite in the concentrated NaOH solutions, which will facilitate the research and development of new technologies for reducing energy consumption and alumina production cost.

Quantitative knowledge on the solubility of gibbsite dissolved in Bayer liquors is essential for phase equilibria and thermodynamic properties of hydrated alumina in concentrated NaOH solution. The solubilities of alumina hydrates dissolved in sodium hydroxide solution were reported by RUSSELL et al [1], APPS and NEIL [2], IKKATAI and OKADA [3], POKROVSKII and HELGESON [4]. However, many researchers attempted to develop the thermodynamic model of the NaOH-NaAl(OH)₄-H₂O system to conveniently obtain series of solubility data, since the experimental data are limited and hard to collect in the literatures. The model studies can be divided into two categories. 1) The thermodynamic models based on the physico-chemical properties of the NaOH-NaAl(OH)₄-H₂O system. ZHOU et al [5] measured the osmotic coefficients at 313.2 K for the NaOH-NaAl(OH)₄-H₂O system with the total alkali molality from 0.05 to 12 mol/kg and α_k from 1.64 to 5.53, and obtained Pitzer model parameters by regressing the data. K?NIGSBERGER et al [6] measured the isopiestic of mixed electrolyte solutions involving sodium hydroxide and other components of Bayer liquors at 323.15 K and 373.15 K following Zdanovskii’s rule, and established a predictive thermodynamic model based on Pitzer’s equations. CAIANI et al [7] measured the apparent molar heat capacities of aqueous alkaline solutions of aluminum ion in excess NaOH at temperatures between 323.15 and 523.15 K in the total molality range of 0.3-1.7 mol/kg, and also developed the parameters of the Pitzer ionic interaction model. MAGALH?ES et al [8] measured the specific heat capacities of aqueous NaOH/NaAl(OH)₄ solutions at total stoichiometric ionic strengths of up to 6 mol/kg at 298.15 K and verified the accuracy and adaptability of Pitzer model. 2) Thermodynamic models developed on the solubility data of gibbsite dissolved in NaOH solutions. WESOLOWSKI [9] gave a set of approximate values of pure electrolyte Pitzer model parameters for NaAl(OH)₄(aq) in the temperature range of 273.15-373.15 K , as well as the mixing parameters for Al(OH)₄^- with OH^- and OH^- + Na⁺, by modeling the solubility of gibbsite with the Pitzer ion interaction treatment. LI et al [10,11] introduced the apparent dielectric constant of sodium aluminate solution, and then established a calculation model of activity coefficients according to Debye-Hückel theory.

Despite of the wealth of experimental data for the NaOH-Al₂O₃-H₂O system, few direct studies of the equilibrium constant are available. Consensus has not been reached completely on the values of equilibrium constant, and there is no theoretical model to accurately describe the equilibrium constant. Moreover, the equilibrium constants calculated from solubility data are not exactly equal to the true ones. For example, the calculated equilibrium constant values by WESOLOWSKI [9] agreed well with most of the experimental values of RUSSELL et al [1], but they were obviously greater than those of IKKATAI and OKADA [3]. POKROVSKII and HELGESON [4] modeled all of the previous experimental work and calculated the values of equilibrium constant, which is equivalent to the calculated mean value by ZHOU et al [5]. In this work, the objective was to develop a thermodynamic model to predict the behavior of gibbsite in highly aqueous sodium hydroxide electrolytes solutions, and to provide a theoretical basis of developing new techniques for industrial alumina production. Under these considerations, we attempt to 1) develop a thermodynamic model to describe the equilibrium constant of gibbsite dissolved in NaOH solutions, 2) determine Pitzer model parameters and mixing parameters for the NaOH-NaAl(OH)₄-H₂O system, and 3) assess the applicability of the model proposed.

2 General research thinking

It is known that the Bayer process can be considered an industrial scale recrystallization of gibbsite in the presence of various organic (e.g., oxalate, succinate, acetate) and inorganic (e.g., carbonate, chloride, sulphate) impurities. The composition and structure of aluminate complexes in Bayer liquors have been investigated intensively over the past 120 years. The majority of published works reach the agreement that the pure Bayer liquors consist only of three components [12]: H₂O, NaOH and dissolved Al(III). Several aluminate species, such as Al(OH)₄^-, AlO₂^-, AlO(OH)₂^-, Al(OH)₄^-·2H₂O, Al(OH)₅^2-, Al(OH)₆^3-, Al(OH)₄^-OH^-, Al₂O(OH)₆^2-, [Al(OH)₄]₆^6- and NaAl(OH)₄ have been postulated in the literatures. According to the previous studies [13-15], it is generally agreed that the tetrahedral aluminate ion Al(OH)₄^- is the predominant species in sodium aluminate solution of moderate concentration of 2-4 mol/kg below 373.15 K. Therefore, on the basis of the possible equilibrium among the various species, the actually existing species are Na⁺, Al(OH)₄^-, OH^- and H₂O in an infinitely dilute sodium aluminate solution [5]. The dissolving reaction of gibbsite and sodium hydroxide solutions can be expressed as follows:

The equilibrium constant, K, is

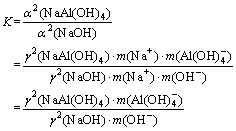        (1)

where

                    (2)

              (3)

                 (4)

Substitution of Eqs. (2-4) into Eq. (1) yields

                      (5)

Equation (5) is a concise expression that combines the equilibrium constant with the molality of NaAl(OH)₄ and NaOH. Logarithmic transformation of Eq. (5) and rearrangement yields

                       (6)

Nowdays, Pitzer and the improved equations are the most widely used models of aqueous electrolytes and the results of Pitzer theory in studying thermodynamic properties are satisfying. According to the ion-interaction approach developed by Pitzer and coworkers [16], the activity coefficient of the NaOH-NaAl(OH)₄-H₂O system is given by:

             (7)

As shown in Eq. (7), there is a mathematical relationship between the values of m and y on the assumption that other items are fixed values. If the Pitzer model parameters, mixing parameters for the system NaOH-NaAl(OH)₄-H₂O and the equilibrium constant for the dissolving reaction are known, we can calculate the value of y for an appointed value of m at various temperatures with the assistance of computer. Consequently, precise knowledge of the equilibrium constant, Pitzer model parameters and mixing parameters for the system NaOH-NaAl(OH)₄-H₂O are essential for prediction of the equilibrium solubility of Al(OH)₃ in concentrated NaOH solutions.

3 Calculation of equilibrium constant of gibbsite dissolved in sodium hydroxide solution

The usual ways [17-19] are to develop an empirical equation to calculate a large number of systematic data covering a wide range of temperatures, since the measured data of equilibrium solubility are limited and difficult to collect. In our early study [11], an empirical equation for calculating equilibrium constant of gibbsite dissolved in sodium hydroxide solution has been proposed. It should be noted that our earlier paper had some mistakes and lacked theoretical basis to some extent. So it is necessary to develop an applicable and efficient model for calculating the equilibrium constant of gibbsite dissolution. The following extended Debye- Hückel equation reported by HELGESON et al [20] is taken as the object of this study:

where

                         (9)

                        (10)

According to Eq. (1) and Eq. (8), the following equation for the NaOH-NaAl(OH)₄-H₂O system is derived:

          (11)

where ?(NaOH)=3.31 ?, ?(NaAl(OH)₄)=3.595 ?; I=[m(Na⁺)+m(Al(OH)₄^-)+m(OH^-)]/2=m(Na⁺); A_γ and B_γ can be obtained through Eq. (9) and Eq. (10). As shown in Eq. (11), providing the influence of pressure is neglected, the term of lg K can be expressed as a function of temperature, so can the term of [b_γ(NaAl(OH)₄)-b_γ(NaOH)]. Thus, the right part of   Eq. (11) can be expressed as a function of temperature (T) and ionic strength (I).

According to the general temperature-dependent equations employed by PABALAN and PITZER [21], and SIMONSON et al [22], the Pitzer model parameters (β⁽⁰⁾, β⁽¹⁾, β⁽²⁾, C^Φ) for NaOH and NaAl(OH)₄ in mixed aqueous electrolytes are applied to the following algorithm:

               (12)

Accordingly, the equations of activity coefficient for NaOH and NaAl(OH)₄ transform into the temperature- dependent expressions. Then, substitution of Eq. (12) into Eq. (1) and rearrangement yield

(13)

Substitution of Eq. (13) into Eq. (11) yields

  (14)

Equations (13) and (14) are temperature-dependent. As the molalities of Al(OH)₄^- and OH^- are fixed values in the NaOH-NaAl(OH)₄-H₂O system for a specific temperature, the item of lg[m(Al(OH)₄^-)/m(OH^-)] in  Eq. (13) is a constant. Furthermore, the second item in the right term of Eq. (14) can also be expressed as a constant. Equations (13) and (14) are then transformed into Eq. (15) and Eq. (16), respectively

              (15)

                (16)

As shown in Eq. (15) and Eq. (16), the equilibrium constant and the modified parameter b_γ are expressed by the temperature-dependent equations. Substitution of  Eq. (15) and Eq. (16) into Eq. (11) and rearrangement yield the final equation:

                 (17)

Equation (17) is a fitting equation corresponding to equilibrium solubility data of gibbsite, where T is absolute temperature (K), and p_i is a fixed value which is obtained by linear regressing. The fitting model has definite theoretical basis which was tested and verified by literature [11]. Furthermore, the new model obtained is better than the previous one due to its brief and improved characteristics. The fixed values of parameters corresponding to Eq. (17) are obtained and listed in Table 1

Table 1 Fixed values of parameters of p₁ to p₈ in Eq. (17)

by linear regressing the selected solubility data in the temperature range of 298.15-373.15 K [1, 9].

Then, the expression of the equilibrium constant of gibbsite dissolved in sodium hydroxide solution in the temperature range of 298.15-373.15 K is given as follows according to Eq. (15) and Table 1.

                    (18)

The values of equilibrium constant were calculated at various temperatures according to Eq. (18), as shown in Fig. 1. And the comparison between the calculated values of lg K and references data was made, as shown in Fig. 2.

It is known that the equilibrium constant is mainly influenced by temperature. The trends of equilibrium constant in Fig. 1 show that the equilibrium solubility of gibbsite increases with the increase of temperature in  the system NaOH-NaAl(OH)₄-H₂O, indicating that temperature adjustment is an effective measure to enrich the caustic solution with a maximum of alumina in digestion and to subsequently drive out a maximum of alumina from the solution in precipitation. Figure 2 presents the calculated and reported data of equilibrium constant of gibbsite dissolved in sodium hydroxide solution. The comparison shows that the calculated values agree well with most of the values of WESOLOWSKI [9] and CHANG [23], indicating that the fitting model is suitable and accurate to predict the equilibrium constant of the dissolving reaction of gibbsite. Details of value assignment can be found in the original paper [11].

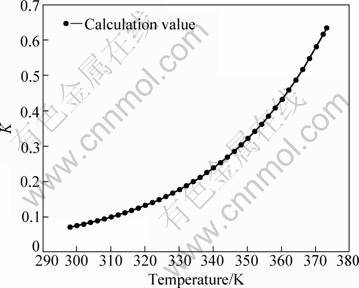
Fig. 1 Equilibrium constant of gibbsite dissolved in sodium hydroxide solution

Fig. 2 Comparison between calculated and reported data for equilibrium constant of gibbsite dissolved in sodium hydroxide solution

4 Development of Pitzer model parameters and mixing parameters for NaOH- NaAl(OH)₄-H₂O system

Many researchers have proposed different methods to calculate the temperature-dependent Pitzer model parameters for the system NaOH-NaAl(OH)₄-H₂O since 1970s. The binary and ternary mixing parameters are also required by the ion-interaction model for calculation of the mixing electrolytes. In the regression analysis, the values of β⁽²⁾(NaOH) and β⁽²⁾(NaAl(OH)₄) are taken to be zero as Refs. [9,21]. It was shown that the items of Pitzer model parameters of NaOH are the opposite number of that of Pitzer model parameters of NaAl(OH)₄ in Eq. (7). Therefore, the items of β⁽⁰⁾(NaOH), β⁽¹⁾(NaOH) and C^Φ(NaOH) must be ascertained in order to regress the items of β⁽⁰⁾(NaAl(OH)₄), β⁽¹⁾(NaAl(OH)₄) and C^Φ(NaAl(OH)₄). Furthermore, the values of the binary mixing parameter of θ(OH^-Al(OH)₄^-) and ternary mixing parameter of ψ(Na⁺OH^-Al(OH)₄^-), which are usually taken as fixed values by researchers [9], are limited and applied to only low concentrations. Precisely, the mixing parameters are taken as the object of regression to testify the influence of the ion-interaction. In the following calculation, Pitzer model parameters for NaOH reported by PABALAN and PITZER [21], as shown in Table 2, are first adopted in this study.

When the Pitzer model parameters for NaOH and the equilibrium constant for the dissolving reaction are known, the Pitzer model parameters for NaAl(OH)₄ and the mixing parameters can be regressed by solving    Eq. (7). The results are listed in Table 3.

As shown in Table 3, the Pitzer model parameters for NaAl(OH)₄, β⁽⁰⁾(NaAl(OH)₄), β⁽¹⁾(NaAl(OH)₄) and C^Φ(NaAl(OH)₄), are temperature-dependent, which was proved by CAIANI et al [7]. The mixing parameters of θ(OH^-Al(OH)₄^-) and ψ(Na⁺OH^-Al(OH)₄^-) are also temperature-dependent, as shown in columns 6 and 7 in Table 3. This is different from that reported by WESOLOWSKI [9] where the values of mixing parameters of θ(OH^-Al(OH)₄^-) and ψ(Na⁺OH^-Al(OH)₄^-) were regarded as a constant of 0.014 and -0.0048 in the temperature range of 273.15-373.15 K, respectively. As the ion-interaction is of electrostatic force with the characteristic of temperature-dependence, the temperature-dependent binary and ternary mixing parameters obtained are reasonable. The results were tested in Ref. [24] which determined the temperature- dependent ψ_ijk functions based on the solubility data and the previously determined values for θ_ij at 298.15 K.

Table 2 Pitzer model parameters for NaOH at different temperatures

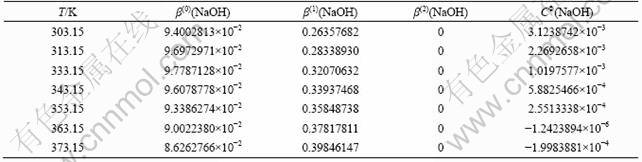
Table 3 Pitzer model parameters for NaAl(OH)₄ and mixing parameters at different temperatures

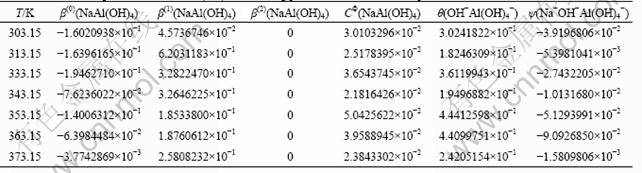
When the Pitzer model parameters for NaOH and NaAl(OH)₄, the binary mixing parameter and ternary mixing parameter are known, all the items of Eq. (7) can be obtained except m and y. Therefore, y can be calculated by solving Eq. (7) with the given value of m by iterative method. The calculated equilibrium solubilities of the NaOH-NaAl(OH)₄-H₂O system at various temperatures are plotted in Fig. 3. Furthermore, the solubility curves can be obtained by Lagrange interpolation method at other temperatures.

As shown in Fig. 3, the molality of NaAl(OH)₄ increases rapidly with increasing the temperature and alkali concentration in Bayer liquors. The value of m(NaAl(OH)₄) at higher temperature is greater than that at lower temperature, and the extent of increase in m(NaAl(OH)₄) is more obvious at higher temperatures.

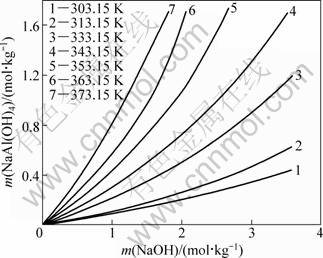
Fig. 3 Equilibrium solubility for NaOH-NaAl(OH)₄-H₂O system at different temperatures

5 Assessment of model applicability

The equilibrium solubilities for gibbsite dissolution were predicted in a relatively wide range of caustic soda concentrations of 0-6 mol/kg at different temperatures in order to testify the precision of the new Pitzer model parameters and mixing parameters. The predicted data were compared with the reported experimental ones [1, 9], as shown in Fig. 4.

Figure 4 shows that good agreement reaches at different temperatures, indicating that the developed model is suitable and accurate to predict the equilibrium solubility of gibbsite dissolved in sodium hydroxide solution. Furthermore, it is necessary to make a comparison between the predicted data of this work and the reported data of references which were not used for developing the Pitzer model parameters and mixing parameters. Combined with the data in Table 2 and Table 3, the Pitzer model parameters for NaOH and NaAl(OH)₄ and the mixing parameters were calculated at 323.15 K by Lagrange interpolation techniques (shown in Tables 4 and 5). Thus, the corresponding equilibrium solubilities of gibbsite dissolution can be obtained at 323.15 K by iterative method with the help of computer, as shown in Table 6.

Table 4 Pitzer model parameters for NaOH at 323.15 K

Table 5 Pitzer model parameters for NaAl(OH)₄ and mixing parameters at 323.15 K

Table 6 Comparison of calculated gibbsite solubility data according to several activity coefficient models over a range of molality of total alkali at 323.15 K

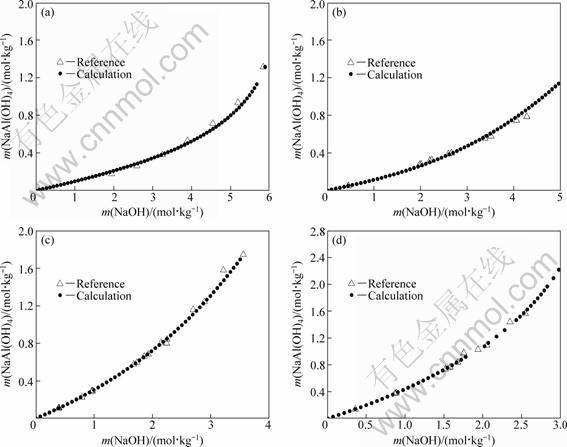
Fig. 4 Comparison between model-predicted and reported solubility of gibbsite at different temperatures: (a) 303.15 K; (b) 313.15 K; (c) 343.15 K; (d) 353.15 K

As shown in Table 6, the equilibrium solubility is also well predicted for the gibbsite dissolved in caustic soda solution at 323.15 K, confirming the reliability and applicability of the model proposed in this study. The method employed in this work provides a theoretical basis to study the behavior of components in sodium aluminate solution and may be extended to the similar systems of uni-univalent electrolytes.

6 Conclusions

1) The equilibrium constant of gibbsite dissolved in sodium hydroxide solution in the temperature range of 298.15-373.15 K can be obtained by the equation:    lg K=-161.1495+4629.7868/T+26.6959ln T-0.0256T.

2) The obtained Pitzer model parameters of β⁽⁰⁾(NaAl(OH)₄), β⁽¹⁾(NaAl(OH)₄) and C^Φ(NaAl(OH)₄) for NaAl(OH)₄, the binary mixing parameter of θ(OH^-Al(OH)₄^-) and the ternary mixing parameter of ψ(Na⁺OH^-Al(OH)₄^-) are all temperature-dependent.

3) New parameters allow the calculation of equilibrium solubility of gibbsite in concentrated NaOH solutions in the temperature range of 298.15-373.15K.

List of symbols

α(NaAl(OH)₄)—Activity of NaAl(OH)₄;

α(NaOH)—Activity of NaOH;

γ(NaAl(OH)₄)—Activity coefficient of NaAl(OH)₄;

γ(NaOH)—Activity coefficient of NaOH;

m(Na⁺)—Molality of Na⁺, mol/kg;

m(Al(OH)₄^-)—Molality of Al(OH)₄^-, mol/kg;

m(OH^-)—Molality of OH^-, mol/kg;

y—Solute mass fraction of NaAl(OH)₄, %;

θ(OH^-Al(OH)₄^-)—Binary mixing parameter for Al(OH)₄^- with OH^-;

ψ(Na⁺OH^-Al(OH)₄^-)—Ternary mixing parameter for Al(OH)₄^- with OH^- and Na⁺;

α₁, α₂—Universal parameters, (kg/mol)^1/2, where α₁=2 (kg/mol)^1/2 and α₂=8 (kg/mol)^1/2;

b_γ—Extended-term parameter;

Z₊—Charge of cation;

Z^_—Charge of anion;

?—Ionic size parameter of electrolyte, ?;

I—Ionic strength, mol/kg;

A_γ—Debye-Hückel solvent parameter, (kg/mol)^1/2;

B_γ—Debye-Hückel solvent parameter, kg^1/2/(mol^1/2·cm);

T—Absolute temperature, K;

ε—Dielectric constant of H₂O;

ρ—Density of H₂O, g/cm³;

A_i—Constant;

C_i—Constant;

p_i—Constant;

β⁽⁰⁾(NaOH), β⁽¹⁾(NaOH), β⁽²⁾(NaOH), C^Φ(NaOH)—Pitzer model parameters for NaOH;

β⁽⁰⁾(NaAl(OH)₄), β⁽¹⁾(NaAl(OH)₄), β⁽²⁾(NaAl(OH)₄), C^Φ(NaAl(OH)₄)—Pitzer model parameters for NaAl(OH)₄.

References

[1] RUSSELL A S, EDWARDS J D, TAYLOR C S. Solubility and density of hydrated aluminas in NaOH solutions [J]. Journal of Metals, 1955, 7: 1123-1128.

[2] APPS J A, NEIL J M. Chemical modeling of aqueous solutions II [M]. Washington D.C.: American Chemical Society, 1990: 414-428.

[3] IKKATAI T, OKADA N. Extractive metallurgy of aluminum [M]. New York: Interscience, 1963: 159-173.

[4] POKROVSKII V A, HELGESON H G. Thermodynamic properties of aqueous species and the solubilities of minerals at high pressures and temperatures: The system Al₂O₃-H₂O-NaCl [J]. American Journal of Science, 1995, 295: 1255-1342.

[5] ZHOU Jun, CHEN Qi-yuan, LI Jie, YIN Zhou-lan, ZHOU Xia, ZHANG Ping-min. Isopiestic measurement of the osmotic and activity coefficients for the NaOH-NaAl(OH)₄-H₂O system at 313.2 K [J]. Geochimica et Cosmochimica Acta, 2003, 67(18): 3459-3472.

[6] K?NIGSBERGER E, K?NIGSBERGER L C, HEFTER G, MAY P M. Zdanovskii’s rule and isopiestic measurements applied to synthetic Bayer liquors [J]. Journal of Solution Chemistry, 2007, 36(11-12): 1619-1634.

[7] CAIANI P, CONTI G, GIANNI P, MATTEOLI E. Apparent molar heat capacity and relative enthalpy of aqueous sodium hydroxoaluminate between 323 and 523 K [J]. Journal of Solution Chemistry, 1989, 18(5): 447-461.

[8] MAGALH?ES M C F, K?NIGSBERGER E, MAY P M, HEFTER G. Heat capacities of concentrated aqueous alkaline aluminate solutions at 25 °C [J]. Journal of Chemical and Engineering Data, 2002, 47(4): 960-963.

[9] WESOLOWSKI D J. Aluminum speciation and equilibria in aqueous solution (I): The solubility of gibbsite in the system Na-K-Cl-OH-Al(OH)₄ from 0 to 100 °C [J]. Geochimica et Cosmochimica Acta, 1992, 56(3): 1065-1091.

[10] LI Xiao-bin, LU Wei-jun, LIU Gui-hua, PENG Zhi-hong, ZHOU Qiu-sheng, MENG Yun, REN Wan-neng. Activity coefficient calculation model for NaOH-NaAl(OH)₄-H₂O system [J]. Transactions of Nonferrous Metals Society of China, 2005, 15(4): 908-912.

[11] LI Xiao-bin, LU Wei-jun, FENG Gang-tao, LIU Gui-hua, PENG Zhi-hong, ZHOU Qiu-sheng, MENG Yun. The applicability of Debye-Hücklel model in NaAl(OH)₄-NaOH-H₂O system [J]. The Chinese Journal of Process Engineering, 2005, 5(5): 525-528. (in Chinese)

[12] SIPOS P. The structure of Al (III) in strongly alkaline aluminate solutions—A review [J]. Journal of Molecular Liquids, 2009, 146(1-2): 1-14.

[13] LI Xiao-bin, WANG Dan-qin, LIANG Shuang, LIU Gui-hua, PENG Zhi-hong, ZHOU Qiu-sheng. Relationship between electric conductivity and ion structure of sodium aluminate solution [J]. Chemical Journal of Chinese Universities, 2010, 31(8): 1651-1655. (in Chinese)

[14] SOAR T J, COUNTER J A, GERSON A R. A static light and X-ray scattering study of supersaturated caustic aluminate liquors [J]. Langmuir, 2000, 16(11): 4784-4791.

[15] LI Xiao-bin, WANG Dan-qin, ZHOU Qiu-sheng, LIU Gui-hua, PENG Zhi-hong. Concentration variation of aluminate ions during the seeded precipitation process of gibbsite from sodium aluminate solution [J]. Hydrometallurgy, 2011, 106(1-2): 93-98.

[16] PITZER K S. Activity coefficients in electrolyte solutions [M]. Boca Raton: CRC Press, 1991: 75-153.

[17] LEE Liang-sun, SUN Shiao-lun, LIN Cheng-long. Predictions of thermodynamic properties of aqueous single-electrolyte solutions with the two-ionic-parameter activity coefficient model [J]. Fluid Phase Equilibrium, 2008, 264(1-2): 45-54.

[18] GE Xin-lei, WANG Xi-dong, ZHANG Mei, SEETHARAMAN Seshadri. A new three-particle-interaction model to predict the thermodynamic properties of different electrolytes [J]. The Journal of Chemical Thermodynamics, 2007, 39(4): 602-612.

[19] MAY P M. Improved thermodynamic calculations for concentrated mixed electrolyte systems including ion pairing (or the absence of it) [J]. Marine Chemistry, 2006, 99(1-4): 62-69.

[20] HELGESON H C, KIRKHAM D H, FLOWERS G C. Theoretical prediction of the thermodynamic behavior of aqueous electrolytes at high pressures and temperatures (IV): Calculation of activity coefficients, osmotic coefficients, and apparent molal and standard and relative partial molal properties to 600 ℃ and 5 kb [J]. American Journal of Science, 1981, 281(10): 1249-1516.

[21] PABALAN R T, PITZER K S. Thermodynamics of NaOH(aq) in hydrothermal solutions [J]. Geochimica et Cosmochimica Acta, 1987, 51(4): 829-837.

[22] SIMONSON J M, MESMER R E, ROGERS P S Z. The enthalpy of dilution and apparent molar heat capacity of NaOH(aq) to 523 K and 40 MPa [J]. Journal of Chemical Thermodynamics, 1989, 21(6): 561-584.

[23] CHANG B T. Determination of thermodynamic properties of gibbsite from its solubility data in NaOH solutions [J]. Bulletin of the Chemical Society of Japan, 1981, 54: 1960-1963.

[24] PABALAN R T, PITZER K S. Heat capacity and other thermodynamic properties of Na₂SO₄(aq) in hydrothermal solutions and the solubilities of sodium sulfate minerals in the system Na-Cl-SO₄-OH-H₂O to 300 °C [J]. Geochimica et Cosmochimica Acta, 1988, 52(10): 2393-2404..

三水铝石在氢氧化钠溶液中的平衡溶解度热力学模型

李小斌，阎 丽，周秋生，刘桂华，彭志宏

中南大学 冶金科学与工程学院，长沙 410083

摘  要：针对拜耳法生产氧化铝过程中最为重要的NaAl(OH)₄-NaOH-H₂O体系，构建三水铝石溶解于氢氧化钠溶液的反应平衡常数的理论模型，并得出电解质NaAl(OH)₄ 新的Pitzer模型参数和NaOH-NaAl(OH)₄-H₂O体系的热力学混合参数(温度范围298.15~373.15 K)。将所得模型和参数对NaAl(OH)₄-NaOH-H₂O体系进行适用性分析。结果表明：将该理论模型用来计算三水铝石溶解反应的平衡常数是适用且准确的；电解质NaAl(OH)₄的Pitzer模型参数β⁽⁰⁾(NaAl(OH)₄)、β⁽¹⁾(NaAl(OH)₄)和C^Φ(NaAl(OH)₄)，Al(OH)₄^-与OH^-的二离子相互作用参数θ(OH^-Al(OH)₄^-)，以及Al(OH)₄^-与 OH^-和Na⁺的三离子相互作用参数ψ(Na⁺OH^-Al(OH)₄^-)均与温度相关；当温度在298.15~373.15 K时，预测三水铝石溶解于氢氧化钠溶液的平衡溶解度是可行的。

关键词：Pitzer模型；铝酸钠溶液；三水铝石；平衡常数；平衡溶解度

(Edited by YUAN Sai-qian)

Foundation item: Project (2005CB6237) supported by the National Basic Research Program of China

Corresponding author: ZHOU Qiu-sheng; Tel: +86-731-88830453; E-mail: qszhou@csu.edu.cn

DOI: 10.1016/S1003-6326(11)61197-7