Crushing analysis and multiobjective crashworthiness optimization of bitubular polygonal tubes with internal walls
来源期刊:中南大学学报(英文版)2016年第11期
论文作者:高广军 李健 邹翔 关维元
文章页码:3040 - 3050
Key words:crashworthiness optimization; thin-walled structure; energy absorption; response surface method; finite element analysis
Abstract: In order to reduce casualties and property losses in a collision accident, thin-walled structure has been extensively used as energy absorber in crashworthiness design of train. With the help of energy absorber, collision kinetic energy can be controllably dissipated by the plastic deformation of structures. A new kind of multi-cell thin-walled structure called as bitubular polygonal tubes with internal walls (BPTIW) was constructed. The crashworthiness characteristics of BPTIWs were investigated by LS-DYNA. It can be found that the BPTIW with 12 sides has the most excellent crashworthiness characteristics. Therefore, based on response surface method (RSM) and multiobjective particle optimization (MOPSO) algorithm, the BPTIW with 12 sides was selected to optimize the dimensions of cross-sectional configuration under different constraints of energy absorption (EA) and crushing peak force (CPF). The results show that the optimal designs of BPTIW12 under different constraints present excellent crashworthiness characteristics and can be used in the practical engineering.
J. Cent. South Univ. (2016) 23: 3040-3050
DOI: 10.1007/s11771-016-3367-7
LI Jian(李健), GAO Guang-jun(高广军), ZOU Xiang(邹翔), GUAN Wei-yuan(关维元)
Key Laboratory of Traffic Safety on Track of Ministry of Education (School of Traffic & Transportation Engineering, Central South University), Changsha 410075, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: In order to reduce casualties and property losses in a collision accident, thin-walled structure has been extensively used as energy absorber in crashworthiness design of train. With the help of energy absorber, collision kinetic energy can be controllably dissipated by the plastic deformation of structures. A new kind of multi-cell thin-walled structure called as bitubular polygonal tubes with internal walls (BPTIW) was constructed. The crashworthiness characteristics of BPTIWs were investigated by LS-DYNA. It can be found that the BPTIW with 12 sides has the most excellent crashworthiness characteristics. Therefore, based on response surface method (RSM) and multiobjective particle optimization (MOPSO) algorithm, the BPTIW with 12 sides was selected to optimize the dimensions of cross-sectional configuration under different constraints of energy absorption (EA) and crushing peak force (CPF). The results show that the optimal designs of BPTIW12 under different constraints present excellent crashworthiness characteristics and can be used in the practical engineering.
Key words: crashworthiness optimization; thin-walled structure; energy absorption; response surface method; finite element analysis
1 Introduction
For the safety protection of occupants during a train collision accident, the collision energy needed to be dissipated in a stable and orderly way. The common method is to install specific energy absorption structure in the end of railway vehicle. The thin-walled mental structures, for its high strength-weight ratio, low cost and high energy absorption efficiency, are widely used in the crashworthiness design of railway vehicle [1]. The crashworthiness characteristics of thin-walled mental structures draw more and more attentions [2-3].
The thin-walled mental structure mainly dissipates collision energy by plastic deformation. Therefore, compared with single circular or square tube, the multi-cell columns have the higher energy absorption efficiency and better deformation stability. Besides, the state-of-the-art extrusion process makes the fabricating of complex multi-cell tubes feasible. Hence, some considerable study has been conducted on the energy absorption of multi-cell tubes in recently years. For example, based on the super folding element theory, ZHANG et al [4] derived a theoretical solution for the mean crushing force of multi-cell sections, which was validated by finite element simulation. ALAVI NIA and PARSAPOUR [5] investigated the crashworthiness of single cell and multi-cell tubes, and showed that adding partitions at corners did help to improve the crash behaviors, they also revised Zhang’s formula to inclusion of unequal cells square tubes. NAJAFI and RAIS- ROHANI [6] studied the crushing performance of thin-walled aluminum tubes with different multi-cell, multi-corner configurations under axial quasi-static loading condition. SHARIFI et al [7] investigated the energy absorption of bitubal circular tube, which consisted of two AL-6063-O tubes with unequal diameters placed coaxially, it was found that the maximum crushing load and the absorbed energy in the bitubal energy absorbers were approximately equal to the summation of that of each tube independently. QIU et al [8] studied the crash behaviors of different multi-cell hexagonal cross-sectional columns under axial and oblique loads, and complex proportional assessment was used to select the best possible sectional configuration under multiple loading angles, then multiobjective particle optimization algorithm was employed to optimize the dimensions of such a cross-sectional configuration.
From the abovementioned study, it is known that the multi-cell structure has good energy absorption characteristics. Hence, this work puts forward a new multi-cell structure: bitubular polygonal tube with internal walls (BPTIW), which consists of the inner polygonal tube, the outer polygonal tube and the internal walls connected the inner tube and the outer tube at the corner. Compared with traditional multi-cell square tube, it can produce more folds under axial loading, which will lead to a better energy absorption. In order to get the best configuration under different constraints, their crashworthy characteristics are evaluated by finite element simulation firstly. Then, different crashworthiness indicators are introduced to select the best possible sectional configuration. Subsequently, a high-order response surface model is constructed to precisely establish the relationship between the objective functions of the energy absorption as well as crushing peak force and the geometrical design variables of the selected configuration. Finally, based on the high-order response surface model, the designs with different optimization criterions are achieved by multiobjective particle optimization (MOPSO) algorithm.
2 Crashworthiness indicators
In order to evaluate the crashworthiness of the energy absorption structure, it is essential to define the crashworthiness indicator. Typically, energy absorption (EA), specific energy absorption (SEA), crash load efficiency (CLE) and energy absorption of per unit area (EAUA) are commonly used as indicators. The EA of a structure can be calculated by
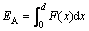 (1)
(1)
where F(x) denotes the instantaneous crushing force in the axial direction; d denotes the crushing displacement. In this work, the value that the crushing force begins to rapidly increase is adopted.
Specific energy absorption (SEA) is widely used to estimate the energy absorption efficiency of structures with different materials and weights, and it can be calculated by
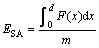 (2)
(2)
where m is the mass of the structure.
Crash load efficiency (CLE) is another important crashworthiness indicator, it is defined as a ratio of the mean crushing force (MCF) to crushing peak force (CPF), which can be calculated by
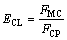 (3)
(3)
where FCP denotes the maximum crushing force during the crushing of the energy absorption structure; FMC is the mean crushing force, which can be calculated by
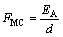 (4)
(4)
In order to evaluate the space utilization efficiency of the structure, energy absorption of per unit area (EAUA) is introduced, it is defined as a ratio of the energy absorption (EA) to cross section area (CSA), which can be calculated by
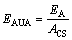 (5)
(5)
where ACS is the cross section area of the energy absorption.
3 Finite element modeling
3.1 Geometrical description
The structure investigated is bitubular polygonal tubes with internal walls subjected to axial impact loading. For simplicity, they are named as BPTIW (abbreviate of bitubular polygonal tubes with internal walls). A typical geometry of BPTIW is shown in Fig. 1, which consists of the inner polygonal tube, the outer polygonal tube and the internal walls connected the inner tube and the outer tube at the corner, and the circumcircle diameter (DC) of the inner tube is half to that of the outer tube. All the cross-sectional configurations of BPTIWs with the same length of 500 mm and the same thickness of 2 mm to be analyzed here are shown in Fig. 2. These tubes have different side numbers and are assigned different circumcircle diameters to keep the tubes with the same mass. At the same time, a typical multi-cell square tube is used to validate the accuracy of finite element model. All the tubes are crushed from the top ends of the tubes by a rigid wall at a constant velocity, the crushing velocity is set to 1 m/s to reduce the effect of inertial effect on the deformation of the tubes, the bottom ends of the tubes are fully attached to the fixed rigid ground, the corresponding schematic of the computational model is shown in Fig. 3.
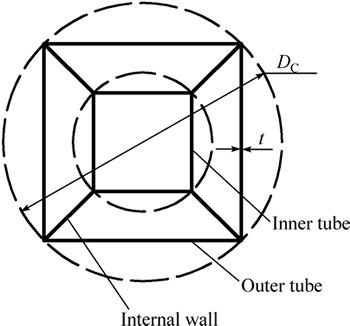
Fig. 1 Typical geometry of BPTIW
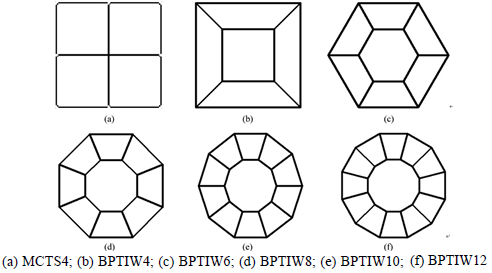
Fig. 2 Cross-sectional configurations of MCTS4 and BPTIWs:
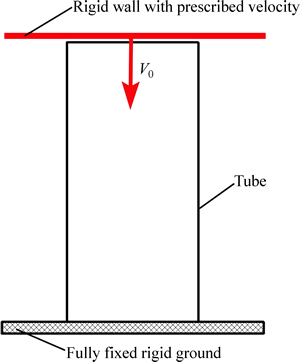
Fig. 3 Schematic of computational model
3.2 Material properties
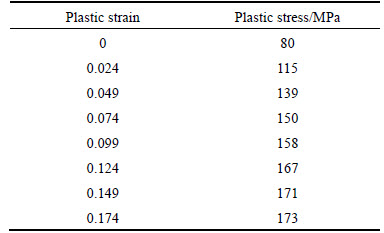
The material of BPTIWs is aluminum alloy AA6060-T4 with mechanical properties of density ρ=2700 kg/m3, elastic elastic modulus E=68.2 GPa, Poisson ratio v is 0.3, initial yield stress σy=80 MPa, ultimate stress σu=173 MPa [9]. The constitutive model of aluminum alloy AA6060-T4 is based on an elastic-plastic material model with von Mises’s yield criterion. In this material constitutive model, the plastic hardening of the material is defined by several pieces lines, and the corresponding pairs of the plastic strain and plastic stress are given in Table 1. Since the aluminum alloy is insensitive to strain rate [10], the strain rate effect in the finite element model is neglected.
Table 1 Strain hardening data for AA6060 T4 [9]
3.3 Finite element models
The finite element models are established by explicit nonlinear finite element code LS-DYNA. The tube is modeled by Belytschko-Tsay four-node shell elements with five integration points through the thickness and one point in the element plane.
For the finite element simulation analysis is based on the grid discretization of the structure, the grid has great effect on the result of simulation. In order to find the optimum mesh size for the numerical simulation, a mesh convergence analysis is performed. The energy absorption of MCTS4 under axial impact loading predicted by different element sizes and the relative errors with respect to the result of 3.5 mm×3.5 mm are listed in Table 2. It can be seen from Table 2 that convergent solution is achieved when the element size is smaller than 4.0 mm×4.0 mm. Similar results are obtained for other crashworthiness indicators. Hence, the element size of 4.0 mm×4.0 mm is sufficient accuracy and it is adopted in the finite element model.
Table 2 Energy absorption of MCTS4 predicted by different element sizes

The explicit nonlinear finite element code LS-DYNA is well suited to simulate post-buckling problems where complex contact interactions occur within a structure as it collapses [11]. The rigid wall is achieved by the RIGID_WALL_GEOMETRIC_FLAT_ MOTION card in LS-DYNA. An automatic sing-surface contact is adopted to account for the self-contact of the tube during deformation, and the contact between the tube and the rigid wall is achieved by automatic node-to-surface contact, the static and dynamic friction coefficient is set to be 0.3 and 0.2, respectively.
4 Numerical results and discussion
4.1 Validation of finite element model
In order to validate the finite element model, the numerical results of the MCTS4 under axial loading will be compared with the theoretical results developed by ZHANG et al [4]. Based on their work, the expression for predicting the mean crushing force of empty multi-cell square tube under quasi static loading can be written as
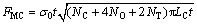 (6)
(6)
where σ0 is the yield stress; t is the thickness of the tube; NC, NO and NT denote the number of corner, crisscross and T-shape in the cross-section of the multi-cell square tube, respectively; LC is the total length of the wall of the cross-section. An enhancing coefficient was proposed by LANGSETH and HOPPERSTAD [12] to account for the inertia and strain rate effects of the tube under dynamic loading, and it is in the range of 1.3-1.6 for AA6064 T4 tubes under the crushing velocity of 8-20 m/s without trigger. However, the crushing velocity in this work is 1 m/s, so the enhancing coefficient is not considered. The results of finite element simulation by LS-DYNA and theoretical analysis are shown in Fig. 4.
It can be seen from Fig. 4 that the MCTS4 presents a stable and orderly deformation mode. An initial peak force appears at the beginning of the crushing of the structure. Subsequently, with the stable formation of fold, the crushing force fluctuates at a certain degree until the structure is fully compacted. The mean force obtained by LS-DYNA is in good agreement with that obtained by theoretical analysis, when the crushing displacement is 350 mm, the mean force obtained through simulation is 55.73 kN and the result derived through Eq. (6) is 56.79 kN, the relative error is 1.87%, which shows that the result of finite element model established above is credible.
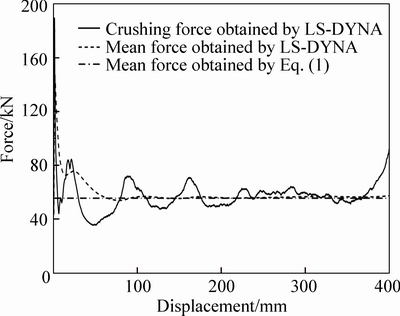
Fig. 4 Crushing force-displacement curve of MCTS4
4.2 Deformation process and force-displacement curves of BPTIWs
As an energy absorption structure, stable and orderly deformation process is an important evaluation index of structure crashworthiness. Figure 5 displays the deformation process of different BPTIWs under constant axial impact load. It is found that each BPTIW presents progressive collapse mode and the number of folds increases with the increasing edges of polygon. Figure 6 depicts the corresponding force-displacement curves of BPTIWs, all the curves have the same change process and trend. Firstly, the curves present a significant initial crushing peak force, which is caused by the inertial effect and initial deformation. After that, with the progressive collapse of the structure, the crushing forces decrease rapidly and fluctuate at a certain degree. Finally, the crushing forces increase rapidly with the compaction of the structure. Meanwhile, with the increasing edges of polygon, the curves have more fluctuations and their periods of folding are shorter, which is corresponding to the fact that their folding lengths are shorter and the folding numbers are more as shown in Fig. 5. Furthermore, it is apparent that the force increases significantly with the increasing edges of polygon, which shows that the more edges of BPTIW has the higher energy absorption ability with the same mass, its energy absorption efficiency is higher.

Fig. 5 Deformation process of BPTIWs:
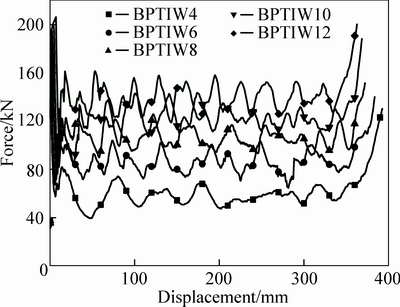
Fig. 6 Force-displacement curves of BPTIWs
4.3 Crashworthiness comparison of BPTIWs
In the present study, a range of BPTIWs with the same wall thickness and mass, but different in configurations is investigated by LS_DYNA. The crashworthiness characteristics of these structures are compared to get the best configuration. The crashworthiness indicators, FCP, EA, EAUA and FCL are shown in Table 3. From Table 3, it is clear that the BPTIW12 has the highest FCP. Furthermore, for the wall thickness and mass are the same, it also indicates that the FCP is affected by the configuration of the structure. At the same time, it can also be found that the BPTIW12 has the highest EA, whose energy absorption is 46.69 kJ, when compared with BPTIW4, it increases by 115.16%, which means that a more compact structure has better energy absorption efficiency. As for the EAUAs, that of BPTIW12 is 2535.96 kJ/mm2, which is also the highest. For the same wall thickness and mass, the compact structure has the smaller cross sectional area, whereas, the compact structure also has a higher energy absorption ability, so the BPTIW12 in EAUA is obvious superior to other structures. Finally, the FCL of BPTIW12 is also the highest, which reaches 0.67, its value is very high in the crushing energy absorption of thin-walled structure.
Table 3 Crashworthiness indicators of MCTS4 and BPTIWs
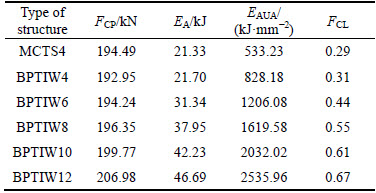
Above all, the BPTIW12 has better crashworthiness indicators in EA, EAUA and FCL than other BPTIWs, it can be used as an excellent energy absorber in crashworthiness design of structure. In the following section, the BPTIW12 will be optimized under different optimization objectives to seek for the best parameters of wall thickness t and circumcircle diameter DC.
5 Multi-objective optimization of BPTIW
5.1 Description of optimization problem
As an energy absorber, it is expected to absorb as many energies as possible, so EA is identified as an objective function and expects to be maximized. Meanwhile, FCP usually lead to a high deceleration and thus causes severe injury to the occupants [13], thus the FCP is set to be as another objective function and expects to be minimized in the optimization problem. Furthermore, the optimization objective and corresponding constraint condition may be different in practice, hence the single-objective and multi-objective optimization of the structure will be studied in detail.
5.1.1 Single-objective optimization
In practical engineering applications, it always shows the problem that the FCP is less than a certain value and expects to maximize the EA, or the EA is greater than a certain value and expects to minimize the FCP. They can be expressed as Eq. (7) and Eq. (8), respectively.
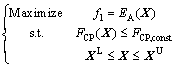 (7)
(7)
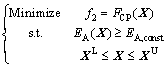 (8)
(8)
where FCP,const and EA,const are given as the constraints of crushing peak force and energy absorption, respectively; XL and XU are the lower and upper bounds of the design variable vector X, respectively.
5.1.2 Multi-objective optimization
For multi-objective optimization problem, in order to make the different optimization target to be comparable, its values will be normalized. At the same time, the importance of each optimization target is evaluated by weight, the common weighting methods are linear weighted average method and geometrical average method, based on the above weighting methods, the corresponding optimization problem can be expressed as Eq. (9) and Eq. (10), respectively.
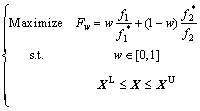 (9)
(9)
where 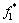 and
and 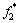 are the given normalizing values of EA and FCP, respectively; w is the weight factor, which is used to evaluate the importance of each objective.
are the given normalizing values of EA and FCP, respectively; w is the weight factor, which is used to evaluate the importance of each objective.
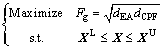 (10)
(10)
where Fg is the overall efficiency coefficient; dEA and dCPF are the efficiency coefficient of EA and FCP, respectively. The calculation of dEA and dCPF can be expressed as Eq. (11) and Eq. (12) .
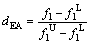 (11)
(11)
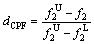 (12)
(12)
where fL and fU are the lower and upper bounds of the objective function in the design space, respectively. At the same time, higher efficiency coefficient means better optimization result. When the overall efficiency coefficient Fg reaches 1, it means that the corresponding objective function achieves the optimal solution; whereas Fg is 0, which indicates that it is the worst solution.
5.2 Design of experiment
Design of experiment (DoE) provides a means to select the sampling points in the design space. There are many different experimental design methods available, such as full factorial design, Latin hypercube, and central composite design or D-optimal design [14-17]. The full factorial design method is used to sample the design points in this work for the advantage of its uniformity [18]. In this work, as shown in Table 4, 25 design samples are generated by the full factorial design method.
5.3 Metamodel establishment
In the crashworthiness optimization of thin-walled structure, it is difficult to establish the analytical formation between the objective function and design variable, so the metamodel, such as response surface method (RSM), is extensively used, which has been proved particularly effective[19-20]. In this study, RSM is used to predict the response of EA and FCP on the wall thickness t and circumcircle diameter DC of the thin- walled structure.
Table 4 Sampling design points and crashworthiness indicators of BPTIW12

Response surface method (RSM) is a method to describe the function relation between response variable and input variable, and it can be expressed by
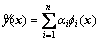 (13)
(13)
where x denotes the design variable; 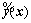 denotes the approximation function of the real response;
denotes the approximation function of the real response; 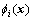 denotes the basis function; αi denotes the corresponding coefficient of
denotes the basis function; αi denotes the corresponding coefficient of 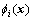 . Usually, polynomial functions are used as the basic function for simplify. The accuracy of RSM depends on the order of polynomial function and the number of sampling points.
. Usually, polynomial functions are used as the basic function for simplify. The accuracy of RSM depends on the order of polynomial function and the number of sampling points.
In order to get the coefficient of basis function αi, the finite element analyses on sampling points are needed. Then we can get the response vector y(x), the error between approximation function 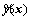 and response y(x) can defined in Eq. (14).
and response y(x) can defined in Eq. (14).
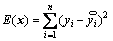 (14)
(14)
In order to minimize the error E(x), the least square method is applied to Eq. (14), and then the coefficient α can be calculated by Eq. (15).
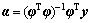 (15)
(15)
where the matrixes φ and y can be calculated by Eq. (16) and Eq. (17), respectively.
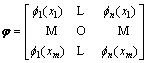 (16)
(16)
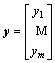 (17)
(17)
By substituting Eq. (15) to Eq. (13), the RS model is fully determined, which establishes the relationship between response function and design variable.
5.4 Accuracy evaluation of metamodel
The numerical errors of the RS model can be caused by the selection of basic function, number of sampling points and the least square [21]. Therefore, in order to evaluate the accuracy of metamodel, several evaluation criterions, including the relative error (ER), the root mean square error (ERMSE), the max absolute error (EMAX), the R square values, are introduced. They can be calculated as follows:
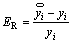 (18)
(18)
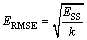 (19)
(19)
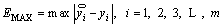 (20)
(20)
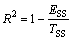 (21)
(21)
where k is the number of sampling points; ESS and TSS are the sum of squared errors and the total sum of squares, respectively. They can be calculated by Eq. (22) and Eq. (23).
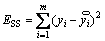 (22)
(22)
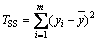 (23)
(23)
where 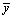 is the mean of yi.
is the mean of yi.
At the same time, the above evaluation parameters may not be completely independent on each other, and the smaller the values of ER, ERMSE and EMAX are or the larger the value of R2 is, the more accurate the metamodel is. Besides, the parameter ERMSE is used to evaluate the overall accuracy of the metamodel and the parameter of EMAX is used to evaluate the local accuracy of the metamodel.
5.5 Optimization algorithm
In order to solve the optimization problem in this work, a suitable optimization algorithm is needed. Compared with the optimization algorithms such as nondominated sorting genetic algorithms (NSGA) [22], Pareto archived evolution strategy (PAES) [23], the multiobjective particle swarm optimization (MOPSO) has drawn considerable attention recently due to its relatively fast convergence and well-distributed Pareto front. The MOPSO algorithm is proposed by COELLO et al [24] and it has been successfully used to solve the crashworthiness optimization of thin-walled structure such as functionally graded foam-filled structures [25] and the sheet metal forming problems [26]. In this work, the MOPSO is utilized to obtain the Pareto front of the two conflicting objectives of EA and FCP. Actually, the Pareto front is a set of the non-dominated optimal solutions and the engineers can make their own decisions according to the actual demand.
6 Results and discussion
6.1 Error analysis of metamodel
In order to establish the metamodel of optimization problems, 25 design points are sampled in the design space by the full factorial design method and the corresponding objective values are shown in Table 5. According to the methodology mentioned in Section 5.3, the RS models with orders ranging from 1 to 4 for EA and FCP are established. By using Eqs. (18)-(21), the accuracy of RS models with different orders are listed in Table 5. It is apparent that the quartic polynomial function has the best accuracy for EA and FCP, and its maximum relative errors of EA and FCP are 0.9954% and 0.2154%, respectively, which is complete acceptable in engineering application. Therefore, the quartic polynomial functions are used in the following optimization design process, and the RS models of EA and FCP can be written as Eq. (24) and Eq. (25).
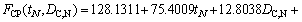
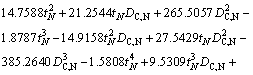
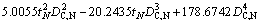 (24)
(24)
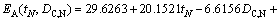
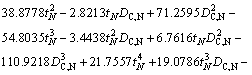
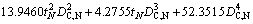 (25)
(25)
where tN and DC,N are the normalized wall thickness and the normalized circumcircle diameter, respectively. tN= (t-1.6)/(2.4-1.6) and DC,N= (DC-120)/(200-120).
6.2 Optimization result
In practical engineering application, the optimization of energy absorber is always based on all kinds of design requirements. Hence, the single objective optimization and multiobjective optimization of energy absorber are carried out in this work.
6.2.1 Single objective optimization
With the explicit formulation FCP (tN, DC,N) of and EA (tN, DC,N), the constrained single objective optimization problems can be defined as Eq. (26) and Eq. (27), respectively.
Table 5 Accuracy of different polynomial RS models

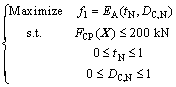 (26)
(26)
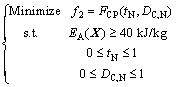 (27)
(27)
By using the constrained single objective particle swarm optimization approach, the optimal results of Eq. (26) and Eq. (27) are shown in Table 6 and Table 7, respectively. From the optimization results, it can be seen that the circumcircle diameter DC=60 mm is an optimum for EA design and FCP design, which shows that the compact structure with progressive deformation process has the higher energy absorption efficiency. However, the optimal wall thickness varies from different design problems. At the same time, in order to validate the optimal result, a finite element simulation is carried out to obtain the values of EA and FCP of the optimal structure, the results are also listed in Table 6 and Table 7, and the relative errors are all less that 1%, which shows that the metamodels of EA and FCP are sufficient accurate and the optimization results are credible. With the constraint of maximizing EA and minimizing FCP, we can also get the Pareto fronts of FCP and EA by multiobjective particle swarm optimization, as shown in Fig. 7. It is apparent that the optimal results of single objective optimization are also the points of Pareto fronts with the corresponding constraint.
6.2.2 Multi-objective optimization
Although the single objective is commonly used in practice, we can’t evaluate the interaction of these criteria, hence the multi-objective optimization is extraordinary necessary. In this work, the multiobjective optimizations of maximizing EA and minimizing FCP by using the linear weighted average and geometrical average methods are carried out.
The multi-objective optimization by using linear weighted average can be defined as Eq. (28).
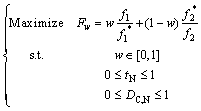 (28)
(28)
where 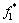 and
and 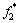 are the given normalizing values of EA and FCP, respectively; w is the weight factor. In this work, the weight factor is set to be 0.5, which means that EA and FCP are the same importance. The optimization results are shown in Table 8, which is also be validated by finite element analysis.
are the given normalizing values of EA and FCP, respectively; w is the weight factor. In this work, the weight factor is set to be 0.5, which means that EA and FCP are the same importance. The optimization results are shown in Table 8, which is also be validated by finite element analysis.
Similarly, the multi-objective optimization by using geometrical average method can be defined as Eq. (29).
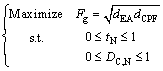 (29)
(29)
where dEA and dCPF can be calculated by Eq. (11) and Eq. (12), respectively.
By maximizing the efficiency cost function Fg, we can get the optimization results, as shown in Table 9. The values of relative efficiency coefficients (dEA and dCPF) and the overall cost function Fg indicate the extent that each objective function approaches its corresponding ideal value. The larger the values of dEA, dCPF and Fg, the better the designs. From the optimization results, we can know that the overall cost function Fg is 0.5785, the relative efficiency coefficients dEA and dCPF are 0.5735 and 0.5836, respectively.
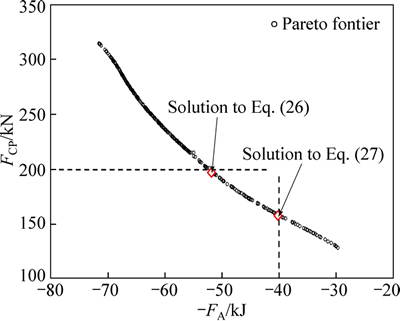
Fig. 7 Pareto fronts of FCP and EA for BPTIW12
Table 6 Optimization results of maximizing EA with FCP constraint (FCP≤200 kN)

Table 7 Optimization results of minimizing FCP with EA constraint (EA≥40 kJ)

Table 8 Multi-objective optimization results by using weight average method

Table 9 Multi-objective optimization results by using efficiency coefficient method

Compared the optimization results by using efficiency coefficient method to that by using weight average method, it is founded that the circumcirlce diameter is the same, but the wall thickness is different, and the values of EA and FCP of optimization results by using efficiency coefficient method are greater than that of optimization results by using weight average method, they are also different to that of single objective optimization. Therefore, as for the same structure, different optimization objectives will obtain different optimization results, the confirmation of optimization objective in practice depends on the actual demand.
7 Conclusions
1) The crash behaviors of BPTIWs with different edges are analyzed by finite element simulation. The results of simulation show that all structures presented stable and orderly deformation process, several crashworthiness indicators, including crushing peak force (FCP), energy absorption (EA), crash load efficiency (FCL) and energy absorption of per unit area (EAUA), are introduced to evaluate the crashworthiness characteristics of BPTIWs. It is found that BPTIW12 has the highest EA, FCL and EAUA, hence it is selected to be optimized.
2) By selecting EA and FCP as the objective variables, circumcircle diameter and wall thickness as the design variables and establishing different orders response surface models the fitting precision increases with the increasing of order, the relative errors of fourth order response surface models of EA and FCP are less than 1%. Therefore, it is selected as the final metamodel.
3) Based on multiobjective particle optimization (MOPSO) algorithm, the optimization problems with different optimization objectives are achieved. It is found that the optimal results of single objective optimization are just the points of Pareto fronts with the corresponding constraint.
4) All optimal solutions were validated by finite element simulation, which also shows that the fourth order response surface models are enough accurate.
References
[1] MARSOLEK J, REIMERDES H G. Energy absorption of metallic cylindrical shells with induced non-axisymmetric folding patterns [J]. International Journal of Impact Engineering, 2004, 30(8/9): 1209-1223.
[2] XIE Su-chao, ZHOU Hui, LIANG Xi-feng, REN Xing. Contrastive analysis and crashworthiness optimization of two composite thin-walled structures [J]. Journal of Central South University, 2014, 21(11): 4386-4394.
[3] DONG Hai-peng, GAO Guang-jun, XIE Su-chao, LI Jian. Collision performance of bitubular tubes with diaphragms [J]. Journal of Central South University, 2015, 22(9): 3657-3665.
[4] ZHANG Xiong, CHENG Geng-dong, ZHANG Hui. Theoretical prediction and numerical simulation of multi-cell square thin-walled structures [J]. Thin-Walled Structures, 2006, 44(11): 1185-1191.
[5] ALAVI NIA A, PARSAPOUR M. An investigation on the energy absorption characteristics of multi-cell square tubes [J]. Thin-Walled Structures, 2013, 68: 26-34.
[6] NAJAFI A, RAIS-ROHANI M. Mechanics of axial plastic collapse in multi-cell, multi-corner crush tubes [J]. Thin-Walled Structures, 2011, 49: 1-12.
[7] SHARIFI S, SHAKERI M, EBRAHIMI FAKHARI H, BODAGHI M. Experimental investigation of bitubal circular energy absorbers under quasi-static axial load [J]. Thin-Walled Structures, 2015, 89: 43-53.
[8] QIU Na, GAO Yun-kai, FANG Jian-guang, FENG Zhao-xuan, SUN Guang-yong, LI Qing. Crashworthiness analysis and design of multi-cell hexagonal columns under multiple loading cases [J]. Finite Elements in Analysis and Design, 2015, 104: 89-101.
[9] SANTOSA S P, WIERZBICKI T, HANSSEN A G, LANGSETH M. Experimental and numerical studies of foam-filled sections [J]. International Journal of Impact Engineering, 2000, 24(5): 509-534.
[10] ZHANG Zong-hua, LIU Shu-tian, TANG Zhi-liang. Comparisons of honeycomb sandwich and foam-filled cylindrical columns [J]. Thin-Walled Structures, 2011, 49(9): 1071-1079.
[11] HALLQUIST J O. LS-DYNA theory manual [M]. California: Livermore Software Technology Corporation, 2006.
[12] LANGSETH M, HOPPERSTAD O S. Static and dynamic axial crushing of square thin-walled aluminium extrusions [J]. International Journal of Impact Engineering, 1996, 18(7/8): 949-968.
[13] LIAO Xing-tao, LI Qing, YANG Xu-jing, LI Wei, ZHANG Wei-gang. A two-stage multi-objective optimization of vehicle crashworthiness under frontal impact [J]. International Journal of Crashworthiness, 2008, 13(3): 279-288.
[14] YANG R J, WANG N, THO C H, BOBINEAU J P. Metamodeling development for vehicle frontal impact simulation [J]. Journal of Mechanical Design, 2005, 127(5): 1014-1020.
[15] WANG G G, SHAN S. Review of metamodeling techniques in support of engineering design optimization [J]. Journal of Mechanical Design, 2007, 129(4): 370-380.
[16] FANG H, RAIS-ROHANI M, LIU Z, HORSTEMEYER M F. A comparative study of metamodeling methods for multiobjective crashworthiness optimization [J]. Computers & Structures, 2005, 83(25/26): 2121-2136.
[17] SONG Xue-guan, SUN Guang-yong, LI Guang-yao, GAO Wei-zhao, LI Qing. Crashworthiness optimization design of foam-filled tapered thin-walled structures using multiple surrogate models [J]. Structural and Multidisciplinary Optimization, 2013, 47(2): 221-231.
[18] HOU Shu-juan, LI Qing, LONG Shu-yao, YANG Xu-jing, LI Wei. Crashworthiness design for foam filled thin-wall structures [J]. Materials & Design, 2009, 30(6): 2024-2032.
[19] YIN Hai-feng, WEN Gui-lin, HOU Shu-juan, CHEN Kai. Crushing analysis and multiobjective crashworthiness optimization of honeycomb-filled single and bitubular polygonal tubes [J]. Materials & Design, 2011, 32(8/9): 4449-4460.
[20] HOU Shu-juan, HAN Xu, SUN Guang-yong, LONG Shu-yao, LI Wei, YANG Xu-jing, LI Qing. Multiobjective optimization for tapered circular tubes [J]. Thin-Walled Structures, 2011, 49(7): 855-863.
[21] HOU Shu-juan, LI Qing, LONG Shu-yao, YANG Xu-jing, WEI Li. Multiobjective optimization of multi-cell sections for the crashworthiness design [J]. International Journal of Impact Engineering, 2008, 35: 1355-1367.
[22] LIAO Xing-tao, LI Qing, YANG Xu-jing, ZHANG Wei-gang, LI Wei. Multiobjective optimization for crash safety design of vehicles using stepwise regression model [J]. Structural and Multidisciplinary Optimization, 2008, 35(6): 561-569.
[23] LIU D S, TAN K C, GOH C K, HO W K. A multiobjective memetic algorithm based on particle swarm optimization [J]. IEEE Transactions on Syetems Man and Cybernetics Part B- Cybernetics, 2007, 37(1): 42-50.
[24] COELLO C A C, PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization [J]. IEEE Transactions on Evolutionary Computation, 2004, 8(3): 256-279.
[25] YIN Han-feng, WEN Gui-lin, WU Xin, QING Qi-xiang, HOU Shu-juan. Crashworthiness design of functionally graded foam-filled multi-cell thin-walled structures [J]. Thin-Walled Structures, 2014, 85: 142-155.
[26] SUN Guang-yong, LI Gguang-yao, GONG Zhi-hui, HE Guan-qiang, LI Qing. Radial basis functional model for multiobjective sheet metal forming optimization [J]. Engineering Optimization, 2011, 43: 1351-1366.
(Edited by DENG Lü-xiang)
Foundation item: Project(CX2016B047) supported by Hunan Provincial Innovation Foundation For Postgraduate, China; Projects(U1334208, 51405516, 51275532) supported by the National Natural Science Foundation of China; Project(2016YFB1200403) supported by the National Key Research and Development Proguam of China
Received date: 2015-12-25; Accepted date: 2016-06-30
Corresponding author: GAO Guang-jun, Professor, PhD; Tel: +86-731-82655294; E mail: gjgao@csu.edu.cn

