J. Cent. South Univ. (2016) 23: 2075-2082
DOI: 10.1007/s11771-016-3263-1
Effect of wind fluctuating on self-starting aerodynamics characteristics of VAWT
ZHU Jian-yang(朱建阳), JIANG Lin(蒋林), ZHAO Hui(赵慧)
School of Machinery and Automation, Wuhan University of Science and Technology, Wuhan 430070, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The present work deals with an investigation of the self-starting aerodynamic characteristics of VAWT under fluctuating wind. In contrast to the previous studies, the rotational speed of the turbine is not fixed, the rotation of the turbine is determined by the dynamic interaction between the fluctuating wind and turbine. A weak coupling method is developed to simulate the dynamic interaction between the fluctuating wind and passive rotation turbine, and the results show that if the fluctuating wind with appropriate fluctuation amplitude and frequency, the self-starting aerodynamic characteristics of VAWT will be enhanced. It is also found that compared with the fluctuation amplitude, the fluctuation frequency of the variation in wind velocity is shown to have a minor effect on the performance of the turbine. The analysis will provide straightforward physical insight into the self-starting aerodynamic characteristics of VAWT under fluctuating wind.
Key words: fluctuating wind; vertical axis wind turbine (VAWT); self-starting performance; weak coupling method; fluctuation amplitude and frequency
1 Introduction
The vertical axis wind turbine (VAWT) has attracted a lot of attentions in recent years because it offers the potential for low-carbon power generation, also for it is considered to possess better aerodynamic characteristics than the horizontal axis wind turbine under the urban environment where the wind is characterized by frequent and often rapid changes in direction and speed [1-6]. Therefore, a good understanding on the effect of wind fluctuating on the aerodynamic characteristics of the blade is very important for designing a VAWT that operates efficiently under urban environment.
MCINTOSH et al [7] conducted a theoretical study (based on multiple stream tube model) to optimize the energy output of VAWT under fluctuating wind conditions. It was shown that a significant increase in energy production can be realized when the tip speed ratio of the turbine is larger than the steady state optimum value.
SCHEURICH and BROWN [8] employed vorticity transport model to investigate the aerodynamic performance and wake dynamics of VAWT in unsteady wind conditions. Different fluctuation amplitudes and frequencies were investigated for three different kinds VAWT: one with a straight-bladed configuration, one with a curved-bladed configuration and another with a helically twisted configuration. The results revealed that the associated power loss is observed when the amplitude of the oscillations in wind speed is high, whereas the frequency of the variation in wind speed is shown to have a minor effect for all practical urban wind conditions.
DANAO et al [9] experimentally tested a wind tunnel scale VAWT with unsteady wind conditions. The results indicated that the unsteady free stream causes a drop in performance of the laboratory scale VAWT. However, only two fluctuation amplitudes of wind (7% and 12% fluctuations) were considered in their study, which is different from the wind conditions of the urban environment. Later, in their another CFD simulations study [10], the effect of different fluctuation amplitudes and frequencies on the performance of VAWT were analyzed. It was found that the unsteady free stream can improve the performance of the VAWT when the mean tip speed ratio is just above the ratio of the steady performance maximum, the amplitude of fluctuation is small, and the frequency of fluctuation is high.
WEKESA et al [11] conducted a numerical study to investigate the aerodynamic performance and physics of flow of the VAWT operating with a fluctuating free-stream. A simple sine wave profile of the free-stream fluctuations was created, and the effects of fluctuation frequency and amplitude on the performance of VAWT were analyzed. The results indicated that the higher frequencies and smaller amplitudes of fluctuation marginally improve the performance of the VAWT.
In summary, many studies have been carried out to study the effect of fluctuating wind on the aerodynamic characteristics of the VAWT, and considerable understands have been achieved; however, most of the aforementioned studies consider the aerodynamic characteristics of the VAWT with constant rotational speed, and the dynamic interaction between the fluid and the turbine rotation which is important for the self-starting aerodynamics characteristics of the VAWT was not analyzed. In this work, we consider a VAWT under fluctuating wind, in contrast to the aforementioned studies in the literature; The present work does not fixed the rotational speed of the turbine, the rotational of the turbine is determined by the dynamic interaction between the fluid and turbine; Therefore, the self-starting aerodynamics characteristics of VAWT with fluctuating wind is investigated. To this end, a weak coupling numerical model is developed to simulate the interaction between the fluid and the passive rotation turbine, and the analysis results of this work will provide useful information for the design of operating efficiently VAWT.
2 Physical model of VAWT and its parameter definitions
Two-dimensional three-blade straight-type VAWT is employed to study the self-starting aerodynamic characteristics of VAWT with fluctuating wind. The schematic of the rotation of the turbine is shown in Fig. 1, where the section blade of the turbine is simplified as NACA0018; ω is the turbine passive rotation speed; R is the rotation radius; Ur is the resultant velocity approaching to the blade section; α is the angle of attack of the blade; θ is the azimuth angle; Ft and Fn are the tangential and normal force, respectively; FL and FD are the lift and drag force. Based on the on the geometry from Fig. 1, the angle of attack α can be defined as
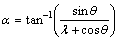 (1)
(1)
where λ is the tip speed ratio which is defined as
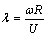 (2)
(2)
where U is defined as
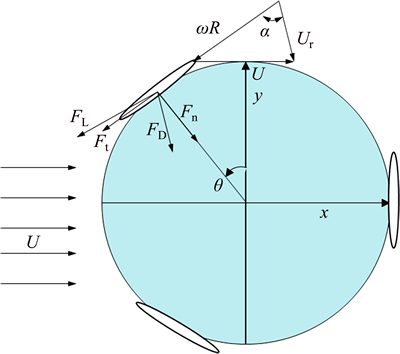
Fig. 1 Schematic of rotation of turbine
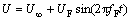 (3)
(3)
where U∞ is steady free stream velocity; UF and fF are the fluctuation amplitude and frequency of the wind, respectively.
The Ft and Fn can be defined as
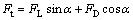 (4)
(4)
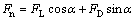 (5)
(5)
The power of the turbine at an arbitrary angular velocity ω is defined as
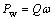 (6)
(6)
where Q is the aerodynamic torque of the turbine, Q= FtR.
While the power coefficient is calculated by
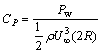 (7)
(7)
where ρ is the fluid density.
By adopting the notation used by MCINTOSH [12], an expression for the number of turbine revolutions per fluctuation can be derived as
 (8)
(8)
where ωS is the turbine passive rotation speed under steady free stream velocity.
Therefore, the mean passive rotation velocity, tip speed ratio and power coefficient of the turbine under fluctuating wind can be calculated by
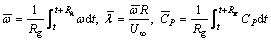 (9)
(9)
Note that when the turbine finishes self-starting process, the positive energy is the energy absorbed by the turbine from wind, and the negative energy is the energy dissipated by the viscous damping force; therefore, only the positive part is considered, and the negative part is fixed at zero.
Besides above parameters, there are another two relative nondimensional parameters which are important for determining the aerodynamics characteristics of VAWT, named Reynolds number Re and solidity σ. The definition of them is described as
 (10)
(10)
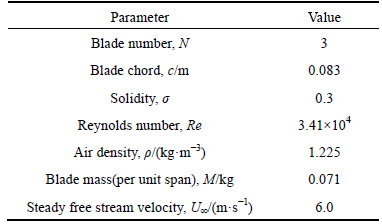
where ν is the fluid kinematic viscosity; N is the number of the turbines; c is the chord of the blade. The key parameters of the turbine are summarized in Table 1.
Table 1 Key parameters of turbine
3 Numerical method for solving interaction between VAWT and fluid
3.1 Solution method
Based on the urban environment of the turbine working in, it is assumed that the flow around the turbine is incompressible and turbulence. In order to simulate the flow around the turbine, RNG k-ε turbulence model which is suggested for VAWT simulation by HOWELL et al [13] and also ALMOHAMMADI et al [14] are employed. The governing equations of the flow around the turbine are solved using the Fluent 6.3 which is based on the finite-volume method. The first-order upwind algorithm is employed for space discretization and first-order implicit algorithm for time discretization. Meanwhile, the coupling between the pressure and the velocity is achieved by means of the SIMPLEC algorithm.
Based on the Newton’s second law, the passive rotation of the turbine is determined by
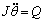 (11)
(11)
where J is the inertia moment of the turbine.
To solve the governing Eq. (11), the finite difference method is employed, where a central difference scheme is applied to discrete the passive rotation angle in Eq. (11), and the equation then becomes:
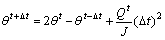 (12)
(12)
where Δt is the iteration time step, and the superscript t+Δt, t and t-Δt indicate a value at the corresponding time step; Qt is the aerodynamic torque at the current moment which can be obtained after the flow field is solved.
A weak coupling method is employed to solve the interaction of fluid and turbine. In this method, at each time step the fluid field is solved first using the solver fluent where the aerodynamic torque on the turbine can be obtained, and then the passive rotation of the turbine under the torque is determined using the finite difference solver which is embedded in fluent using the user defined function (UDF). In the next time step, the fluid flow is solved for the turbine with an updated position and a new aerodynamic torque is obtained. The dynamic mesh technique is used in updating the turbine’s position at each time step. The fluid flow and the turbine’s rotation are solved alternatively. In such a way the fluid flow and the turbine’s rotation are coupled so that the fluid-turbine interaction is taken into account properly. The details of the coupling process are described in Fig. 2.
3.2 Grid generation and boundary conditions
A hybrid (triangular grid and quadrilateral grid) mesh system is employed where a C type computational domain (shown in Fig. 3(a)) containing a outer domain, a middle domain and inner rotation domain is used. To effectively capture the flow field around the turbine, ten rows of boundary layer are used to encompass the entire blades in the rotating domain (shown in Fig. 3(b)) which rotates according to the turbine, and triangular cells are used in the middle domain where remeshing takes place at each time step, the outer domain is keeping stationary for the whole simulation process.
No-slip wall boundary condition is applied on the surface of the blade. The fluctuating wind from left to right is applied to the left computational domain and the boundary condition is given by
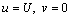 (13)
(13)
The pressure outlet is applied to the right computational domain and the boundary condition is given by
p=P (14)
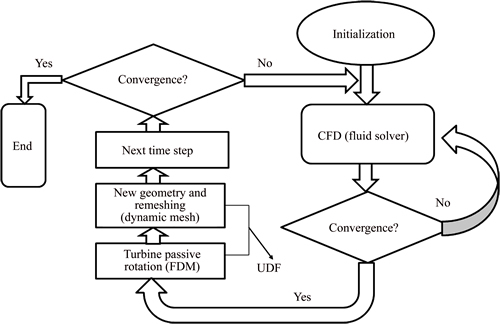
Fig. 2 Schematic of fluid-turbine interaction process
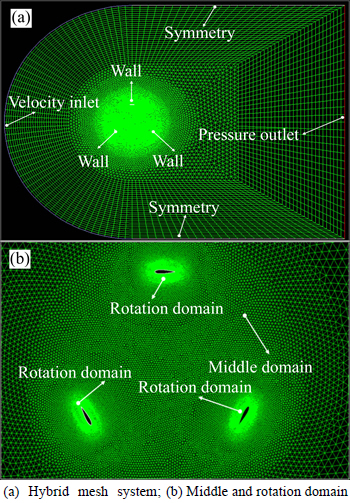
Fig. 3 Mesh system of VAWT:
where P is the fluctuating wind pressure.
The symmetry is applied to the top and bottom computational domain and the boundary condition is given by
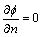 (15)
(15)
where f is the generalized variable, f=[u, v, p, k, ε]; n is the normal direction.
3.3 Method validation
A typically case which was experimental studied by HILL et al [15] and also numerical studied by UNTAROIU et al [16] is employed to test the reliability of the present numerical method for simulating the passive rotation of three bladed straight type VAWT. The simulation parameters are: c=0.083 m, σ=0.664, J= 0.03 kg·m2, U∞=6.0 m/s, UF=0. The resulting passive rotation velocity is plotted against time as shown in Fig. 4, where the result by HILL et al [15] and UNTAROIU et al [16] are also presented, and a nondimensional time t′ which is defined by t′=t/tp (tp is the time when steady rotation velocity ω was established) is employed for comparing. It is seen from the figure that there is magnitude difference betweennumerical results and the experiment data before the self-starting finished. The difference can be due to the combined effects of finite blade length and spokes drag, as described by CASTELLI et al [17]. However, the present numerical result could be able to capture the steady passive rotation velocity correctly. Moreover, the variation of steady passive rotation velocity of the present results is closer to the experiment data than the numerical result by UNTAROIU et al [16] which indicates that the present two-dimensional simulation can grasp the main features of the flow when the turbine finished self-starting.

Fig. 4 Time varies of angular velocity of self-start VAWT under steady wind
4 Results and discussion
In order to study the aerodynamic characteristics of the self-starting VAWT under fluctuating wind, the influence of fluctuation amplitudes and frequencies on the energy coefficient and also flow structure is examined. Three different fluctuation amplitudes are considered, UF=0.01U∞, 0.10U∞ and 0.50U∞, for each of them, and the fluctuation frequency varies the value of 0.5 Hz, 1.0 Hz, 2.0 Hz, 4.0 Hz and 8.0 Hz.
Figure 5 presents the steady cyclical passive rotation established times and mean energy coefficients of the VAWT under different fluctuation amplitudes and frequencies. Three interesting phenomenon can be observed in this figure. First, the disorganized steady cyclical passive rotation established times of the variation of the fluctuation frequency are observed for the turbine under low fluctuation amplitude (UF=0.01U∞); however, for the turbine under moderate and high fluctuation amplitudes, the steady cyclical passive rotation established times increase with the fluctuation frequency increasing. Second, the mean energy coefficients increase with the fluctuation amplitude increasing, whereas the frequency of the variation in wind velocity is shown to have a minor effect for all the considered fluctuating wind in this work. Third, when the wind with appropriate fluctuation amplitudes and frequencies(i.e. UF=0.10U∞ and 0.50U∞, fF<2 Hz), the turbine under fluctuating wind has smaller steady cyclical passive rotation established time and also larger mean energy coefficient, which indicates that appropriate fluctuation amplitude and frequency wind can enhance the self-starting aerodynamic characteristics of the VAWT, and this may be the reason why the VAWT possesses better aerodynamic characteristics than the horizontal axis wind turbine under the urban environment.
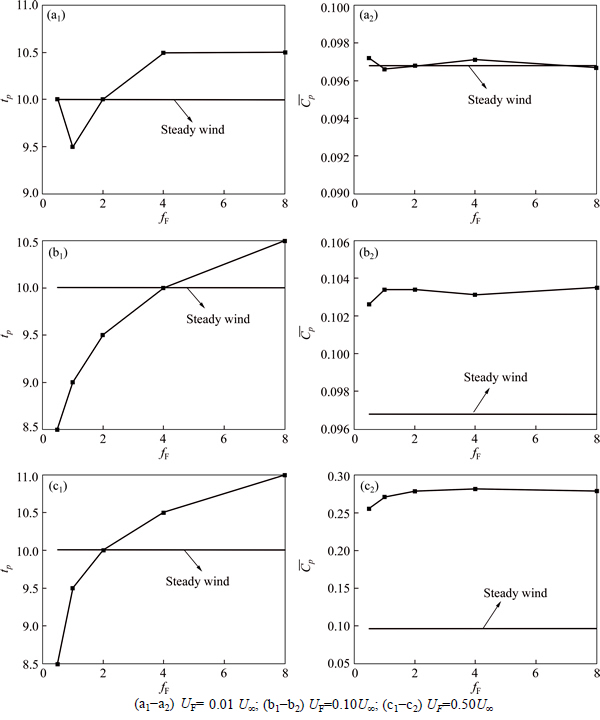
Fig. 5 Mean tip speed ratio and energy coefficient of VAWT with different fluctuation amplitudes and frequencies:
To analyze the mechanism of how the fluctuating wind affects the self-starting aerodynamic characteristics of VAWT, two specific fluctuating winds with UF=0.50U∞, fF=0.5 Hz and UF=0.0, fF=0.0 Hz are studied in details. Note that the fluctuating wind with UF=0.0, fF=0.0 Hz represents steady wind. Figure 6 plots the time history of passive rotation velocity and energy coefficient of the VAWT under these two considered wind conditions. Obviously in Fig. 6 that when the turbine finishs the self-starting, the cyclical passive rotation velocity variation of the time is observed under fluctuating wind, meanwhile the velocity magnitude of the turbine is larger than that under the steady wind almost during the whole self-starting processing. It is also found in the figure that the maximum energy coefficient of the turbine under fluctuating wind has larger amplitude than the turbine under steady wind; however, the coefficient variation of the time is smoother for the turbine under steady wind.
Figure 7 plots the vortices contours of the two case considered above. Two typically time t=2.0 s and 15.0 s are considered. It is seen from Fig. 7(a) that the clear separation vortex can be observed for the turbine both under fluctuating wind and steady wind; however, the intensity of the vortex of the turbine under fluctuating wind has stronger strength than that under steady wind,which is the reason why the turbine under fluctuating wind has larger passive rotation velocity during the self-starting process, as shown in Fig. 6(a). It is seen from Fig. 7(b) that nearly no separation vortex can be observed for the turbine both under fluctuating wind and steady wind; however, the intensity of the vortex of the turbine under fluctuating wind has stronger strength than the turbine under steady wind. It is also found in Fig. 7(b) that the attached vortex of the turbine under fluctuating wind is closer to the blade surface, which indicates that the turbine under fluctuating wind has better delay stall mechanism. According to the study on the bird flight by LIANG and DONG [18] and also WARRICK [19], the delay stall is the reason why the birds produce larger aerodynamic force(the Reynolds number Re of the bird flight is similar to the VAWT considered in this work), which indicates that the unsteady working mechanic of VAWT is similar to the birds flight. This conclusion is consist with the opinion proposed by WORASINCHAI et al [20].
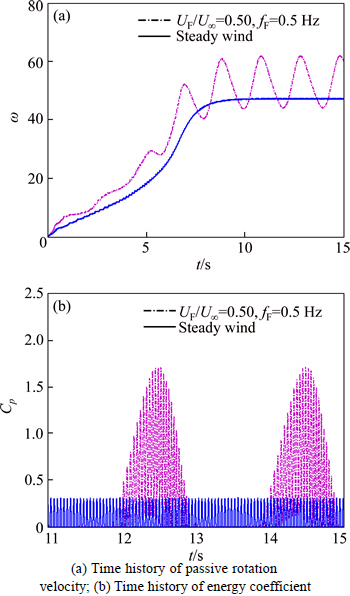
Fig. 6 Time history of passive rotation velocity and energy coefficient of VAWT under fluctuating wind with UF=0.50U∞, fF=0.5 Hz and steady wind:
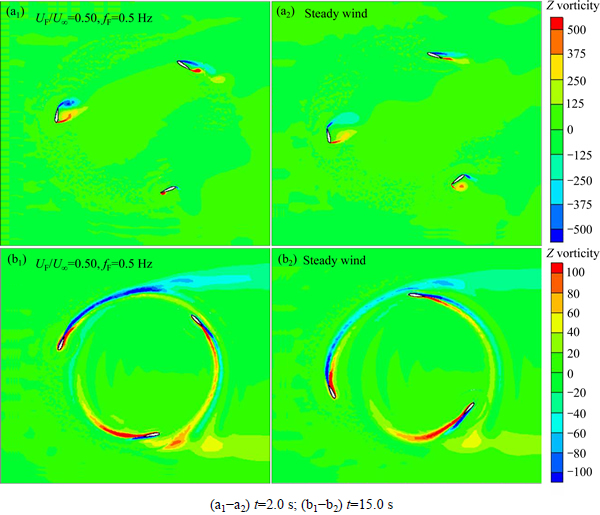
Fig. 7 Vortices contours of VAWT under fluctuating wind with UF=0.50U∞, fF=0.5 Hz and steady wind at t=2.0 s and 15.0 s:
5 Conclusions
A numerical experiment is carried out to investigate the self-starting aerodynamic characteristics of VAWT under fluctuating wind, where the incompressible Navier-Stokes (N-S) equation coupled with passive rotation of the VAWT is solved. The flow field and energy coefficient of the turbine are analyzed for different fluctuation amplitudes and frequencies, and the results show that the fluctuating wind influences the self-starting aerodynamic characteristics of the VAWT greatly. Compared with the fluctuation amplitude, the fluctuation frequency of the variation in wind velocity is shown to have a minor effect on the self-starting aerodynamic characteristics of the turbine. It is also found that when the fluctuating wind with appropriate fluctuation amplitude and frequency (UF=0.10U∞ and 0.50U∞, fF<2 Hz), the turbine will have a smaller steady cyclical passive rotation established time and larger mean energy coefficient. In addition, the stronger vortex and better delay stall mechanism is observed around the turbine under appropriate fluctuation amplitude and frequency wind, therefore, leading to the turbine possessing better self-starting aerodynamic characteristics.
References
[1] MERTENS S, van KUIK G, van BUSSEL G. Performance of an H-Darrieus in the skewed flow on a roof [J]. Journal of Solar Energy Engineering, 2003, 125: 433-440.
[2] MERTENS S. The energy yield of roof mounted wind turbines [J]. Wind Engineering, 2003, 27(6): 507-517.
[3] BALDUZZI F, BIANCHINI A, CARNEVLE E A, FERRARI L, MAGNANI S. Feasibility analysis of a Darrieus vertical-axis wind turbine installation in the rooftop of a building [J]. Applied Energy, 2012, 97: 921-929.
[4] MALAEL I, DUMITRESCU H, CARDOS V. Numerical simulation of vertical axis wind turbine at low speed ratios [J]. Global Journal of Researches in Engineering: I Numerical Methods, 2014, 14(1): 9-20.
[5] BATISTA N C, MELICIO R, MATIAS J C O, CATALAO J P S. Self-start performance evaluation in Darrieus-type vertical axis wind turbines: Methodology and computational tool applied to symmetrical airfoils [C]// ICREPQ’11. Gran Canaria, Spain: ICREPQ, 2011: 1-6.
[6] XU Zhang. Analysis and optimization of a novel wind turbine [D]. UK: University of Hertfordshire, 2013.
[7] MCINTOSH S C, BABINSKY H, BERTENYI T. Optimizing the energy output of vertical axis wind turbines for fluctuating wind conditions [C]// 45th AIAA Aerospace Sciences Meeting And Exhibit. Reno, Nevada, USA: AIAA, 2007: 1007-44.
[8] SCHEURICH F, BROWN R E. Modelling the aerodynamics of vertical-axis wind turbines in unsteady wind conditions [J]. Wind Energy, 2013, 16: 91-107.
[9] DANAO L A, EBOIBI O, HOWELL R. An experimental investigation into the influence of unsteady wind on the performance of a vertical axis wind turbine [J]. Applied Energy, 2013, 107: 403-411.
[10] DANAO L A, EDWARD J, EBOIBI O, HOWELL R. A numerical investigation into the influence of unsteady wind on the performance and aerodynamics of a vertical axis wind turbine [J]. Applied Energy, 2014, 116: 111-124.
[11] WEKESA D W, WANG C, WEI Y J, M.DANAO L A. Influence of operating conditions on unsteady wind performance of vertical axis wind turbines operating within a fluctuating free-stream: A numerical study [J]. Journal of Wind Engineering and Industrial Aerodynamics, 2014, 135: 76-89.
[12] MCINTOSH S. Wind energy for the built environment [D]. Cambridge, UK: University of Cambridge, 2009.
[13] HOWELL R, QIN N, EDWARDS J, DURRANI N. Wind tunnel and numerical study of a small vertical axis wind turbine [J]. Renewable Energy, 2010, 35: 412-422.
[14] ALMOHAMMADI K M, INGHAM D B, MA L, POURKASHAN M. Computational fluid dynamics (CFD) mesh independency techniques for a straight blade vertical axis wind turbine [J]. Energy, 2013, 58: 483-493.
[15] HILL N, DOMINY R, INGRAM G, DOMINY J. Darrieus turbines: The physics of self-starting [J]. Proceedings of the Institution of Mechanical Engineers, Part A: Journal of Power and Energy, 2009, 223: 21-29.
[16] UNTAROIU A, WOOD H G, ALLAIRE P E, RIBANDO R J. Investigation of self-starting capability of vertical axis wind turbines using a computational fluid dynamics approach [J]. Journal of Solar Energy Engineering, 2011, 13: 041010.
[17] CASTELLI M R, ENGLARO A, BENINI E. The Darrieus wind turbine: Proposal for a new performance prediction model based on CFD [J]. Energy, 2011, 36: 4919-4934.
[18] LIANG Zong-xian, DONG Hai-bo. Computational analysis of hovering hummingbird flight [C]// 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition. Florida: Orlando, 2011: 1-8.
[19] WARRICK R D, TOBALSKE B W, POWERS D R, DICHINSON M H. The aerodynamics of hummingbird flight [C]// 45th AIAA Aerospace Sciences meeting and Exhibit, Reno, Nevada: American Institute of Aeronautics and Astronautics, 2007: 1007-44.
[20] WORASINCHAI S, INGRAM G L, DOMINY R G. The physics of H-Darrieus turbine self-starting capability: Flapping-wing perspective [C]// 2012 Proceedings of ASME Turbo Expo, Copenhagen, Denmark: ASME, 2012: 1-10.
(Edited by DENG Lü-xiang)
Foundation item: Projects(61105086, 51505347) supported by the National Natural Science Foundation of China
Received date: 2015-04-19; Accepted date: 2015-09-24
Corresponding author: ZHU Jian-yang, PhD, Lecturer; Tel: +86-15926365381; E-mail: zhujianyang02@163.com