大型冷却塔风荷载干扰系数的取值方法
周旋1,牛华伟1,陈政清1,王振宇2
(1. 湖南大学 风工程试验研究中心,湖南 长沙,410082;
2. 华东电力设计院,上海,200063)
摘要:以国内某电厂超大型冷却塔为研究对象,采用刚性模型测压试验方法获得塔体表面风压时程,通过计算获得各风向角下按不同取值依据得到的干扰系数,探讨合适的取值方法以指导设计。基于风洞试验风压测试数据和有限元时程响应分析得到的位移和应力数据,分别计算群塔状态的干扰系数,比较分析不同干扰系数的特点,进一步基于风压分布积分表达式推导力系数与风压系数之间的关系,并比较研究双塔布置状态下不同干扰系数取值方法之间的差异。研究结果表明:与响应干扰系数相比最大正压干扰系数偏小而最小负压干扰系数偏大,阻力系数干扰系数无法完全衡量壳体响应干扰效应,而通过有限元计算得到的位移或应力干扰系数离散性较小且直接反映风荷载作用效应,推荐设计中以之为依据进行取值。
关键词:冷却塔;风洞试验;刚性模型;干扰系数;双塔干扰
中图分类号:TU317.1;TU311.3 文献标志码:A 文章编号:1672-7207(2014)10-3637-08
Discussion on different methodologies for calculating interference factor of large cooling towers
ZHOU Xuan1, NIU Huawei1, CHEN Zhengqing1, WANG Zhenyu2
(1. Wind Engineering Research Center, Hunan University, Changsha 410082, China;
2. East China Electric Power Design Institute, Shanghai 200063, China)
Abstract: With two super large cooling towers of a domestic power plant to be built, a rigid model was made to obtain wind pressure time history on the tower surface. Different interference factors of several azimuths were calculated by different methods. In order to find an appropriate method to calculate interference factor, the characteristics of different interference factors were compared. Based on wind pressure test data and FEM analysis results of stress and displacement, different interference factors were calculated and compared respectively. Furthermore, based on the wind pressure distribution integral expression, the relationship between the force coefficient and wind pressure coefficient was deduced, and double towers interference was also experimented to compare different interference factors using different calculation methods. The results show that the interference factor calculated by maximum positive pressure coefficient is smaller than that calculated by response, while the interference factor calculated by minimum negative pressure coefficient is larger than that calculated by response. And the interference factor calculated by drag coefficient cannot show shell response interference effect completely. However, using the stress or displacement obtained by FEM analysis to calculate interference factors has smaller discreteness and reflects the interference effect of tower response directly, which is recommended as design basis.
Key words: cooling tower; wind tunnel experiment; rigid model; interference factor; double towers interference
群体间的干扰效应研究最早源自于20世纪30年代,Harris[1]通过大量风洞试验分析发现,帝国大厦周围2条街道上建2个建筑群,将会使得帝国大厦在风荷载作用下的扭矩增加1倍。而后20多年的风工程研究大都集中在单体建筑上,直到1965年英国渡桥电厂冷却塔倒塌事故才重新引起了人们对干扰效应的重视。此后冷却塔的群体干扰效应研究得到迅速发展。Armitt[2]通过试验证明渡桥电厂事故原因正是塔体间的群塔干扰改变了风压分布形式从而使实际应力远大于设计极限。Nimman等[3]通过气弹模型试验了4种干扰工况:高细杆、大厂房、双塔和三塔,计算各工况下基于平均值、均方差、极大值的干扰因子。Orlando[4]针对双塔干扰效应分别对串列、斜列及并列3种工况计算了基于最大或最小风压系数均值的干扰系数,并计算了基于应力极大值的干扰系数。我国冷却塔研究起步较晚,但发展迅速。顾志福等[5]对群塔干扰下平均压力系数分布与脉动压力系数分布进行了系统研究。张军峰等[6]通过气弹模型和刚性模型试验研究了干扰对风荷载特性、力系数及风振效应等的影响;沈国辉等不仅通过数值计算对风荷载干扰特性进行了研究[7],还通过风洞试验对双塔干扰下力系数的平均值与极大值干扰系数进行了研究[8]。在国内外冷却塔设计规范中,以德国VGB规范[9]对冷却塔风荷载的规定较详细,其外表面风荷载表达式为
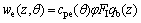 (1)
(1)
式中: 为冷却塔外表面风压设计荷载;
为冷却塔外表面风压设计荷载;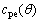 为风压系数;
为风压系数;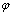 为动态放大系数;
为动态放大系数;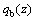 为高度z处的阵风风压;
为高度z处的阵风风压;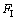 为群体干扰系数,
为群体干扰系数,
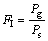 (2)
(2)
Pg为群体干扰参数;Ps为单塔参数。
以不同的参数为依据计算干扰系数的方法不同,目前常用的有“最大正压干扰系数”、“最小负压干扰系数”、“阻力系数干扰系数”、“升力系数干扰系数”等(统称“荷载干扰系数”),以及“应力干扰系数”、“位移干扰系数”等(统称“响应干扰系数”)。国外常以风压系数和应力为指标进行计算,国内沿用高层建筑干扰效应研究的基本思路,常以力系数为指标计算干扰系数。然与高层建筑不同的是,冷却塔属于大型三维壳体结构。用阻力系数求干扰因子来描述基底阻力的干扰效应固然可行,然而,冷却塔设计中更重要的参数是壳体应力及位移等响应值,阻力干扰系数能否准确反映三维壳体响应的干扰效应目前仍值得研究,而且由风压分布曲线中最大正压或最小负压求得的干扰系数能否准确代表偏载风压作用下的响应干扰效应也值得探讨。此外,式(2)中的计算参数可以取极大值也可取平均值,对此目前仍无统一标准。本文作者以某实际工程为例,基于风洞试验和有限元分析,对各种干扰系数取值方法进行比较和探讨。
1 风洞试验概况
1.1 试验模型与测试仪器
某电站拟建有效淋水面积为12 000 m2逆流式自然通风冷却塔,冷却塔通风筒采用双曲线型现浇钢筋混凝土结构,塔顶标高为171.279 m,喉部标高为132.493 m,进风口标高为11.57 m,喉部内面半径为39.73 m,进风口内面半径为64.964 m,两塔中心间距为205.04 m。冷却塔通风筒由52对人字柱与基础连接。本试验在湖南大学HD-2风洞的高速试验段进行。该风洞为闭口回流式矩形截面风洞,试验段长为17.0 m、宽为3.0 m、高为2.5 m。按1:400缩尺比制作冷却塔测压模型及其周边地形与主要建筑模型。冷却塔模型采用合金铝制成,具有足够的强度和刚度,在待测冷却塔外表面沿子午向和环向布置16×36=576个测压点,见图1。
本次试验风速测试采用澳大利亚TFI公司进口的眼镜蛇探针,风速测试精度为0.2 m/s,响应频率达2 kHz以上。风压采集采用美国PSI公司ESP-64电子压力扫描阀,测量精度为0.05%,采样频率不低于325 Hz。
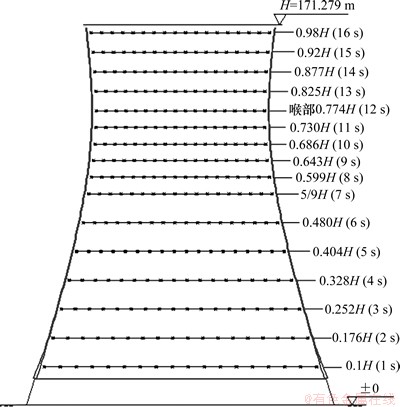
图1 测压模型测点布置图
Fig. 1 Arrangement for pressure points
1.2 风场模拟
本次试验风场按最新修订的GB 50009—2012 《建筑结构荷载规范》中规定的A类地貌模拟,根据相似性要求,风场模拟的主要指标有平均风速剖面、湍流度剖面、顺风向脉动风谱等几个主要参数。考虑到紊流积分尺度与阻塞率的要求本试验的几何缩尺比最终选取1:400,采用“尖劈+粗糙元+格栅条”的方法模拟相应的风场。按Taylor假定计算得到风洞梯度风高度范围内顺风向主积分尺度为0.30~0.43 m[10],换算至实际的积分尺度为120~172 m。风场模拟结果见图2。从图2(a)可知平均风剖面与GB 50009—2012《建筑结构荷载规范》中规定的A类地貌平均风剖面基本一致。紊流度剖面我国规范没有规定,但根据脉动系数计算得到的紊流度比其他国家的规范值小。由图 2(b)可知:2012修订的建筑结构荷载规范中的紊流度较之前有所提高,但仍比日本规范值的小,本次试验紊流度剖面在模型高度范围内基本符合日本规范规定的Ⅰ类风场紊流度剖面。图2(c)所示为转盘中心50 cm高度处顺风向自功率谱。由图2(c)可知该自功率谱与经验谱基本吻合,可见试验风场参数基本满足试验要求。
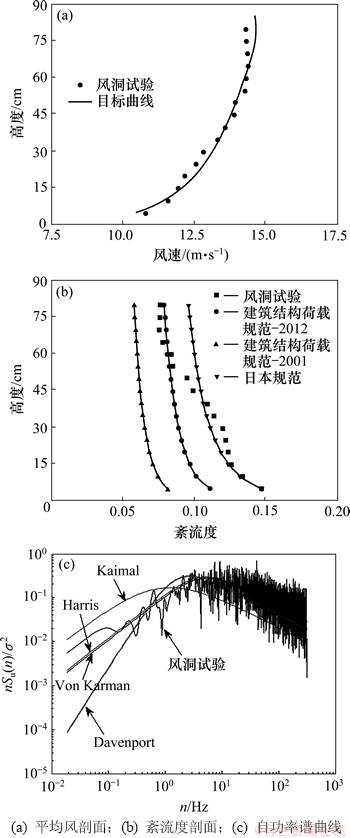
图2 风场模拟结果
Fig. 2 Characteristics of simulated of wind in BLWT
1.3 雷诺数模拟
由于缩尺比较小,此次风洞试验按最大20 m/s风速计算可模拟的雷诺数约为3.36×105相比于实际冷却塔按设计风速计算的雷诺数2.93×108小3个数量级,其中雷诺数的计算以冷却塔1/3壳体高度处直径为特征尺寸。因此,有必要采取措施对雷诺数进行补偿。实践证明,调整模型表面粗糙度能近似模拟高雷诺数状态下绕流特性[11]。本文采用在冷却塔表面粘贴绊线的办法模拟高雷诺数效应,并以德国规范VGB-K1.2风压分布曲线为目标曲线。雷诺效应模拟结果见图3。参照德国规范对粗糙度的定义,K=HR/AR,其中,HR表示肋高即绊线直径,AR表示相邻肋线之间的弧长,已知模型1/3壳体高度处圆环半径为 125.34 mm。
试验如下3种粗糙度,K1=0(光塔),K2=0.009(环向均匀布置36条0.2 mm绊线),K3=0.014(环向均匀布置36条0.3 mm绊线)。试验风速由5 m/s增大至20 m/s,可发现如下现象:1) 随着雷诺数增大,光塔工况的最小体形系数减小而后趋于稳定,而K2和K3工况的最小体形系数增大而后趋于稳定(图3(a));2) 计算1/3壳体高度处的截面阻力系数,随着雷诺数增大,光塔工况的阻力系数陡然下降而后趋于稳定,而粗糙度K2工况的阻力系数先下降后上升,粗糙度K3工况的阻力系数基本不变(图3(b))。说明粗糙度由0增大到0.014,绕流状态由临界变为了超临界,实现了低雷诺数下对高雷诺数绕流状态的模拟。最终得到粗糙度为K3时喉部测层的体形系数,与目标曲线吻合较好(图3(c))。
2 干扰系数取值探讨
2.1 平均值干扰系数与极大值干扰系数
目前国内外诸多文献在计算干扰系数时都会列出均值干扰系数与极值干扰系数[4, 8],即式(2)中参数取平均值或极大值计算。本文认为,干扰系数取均值或极值计算均可,但必须同时考虑风振系数。长期以来风振系数与干扰系数都是单独考虑,而实际风振响应与干扰密切相关。由文献[4]可知实际上干扰因子与风振系数的作用是将群塔效应下最大响应的极值,转换为单塔最大响应均值进行计算,用公式表示为
 (3)
(3)
式中: 为群塔下最大响应的极值;
为群塔下最大响应的极值; 为单塔最大响应均值;
为单塔最大响应均值;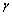 为干扰因子;
为干扰因子;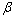 为风振系数。
为风振系数。
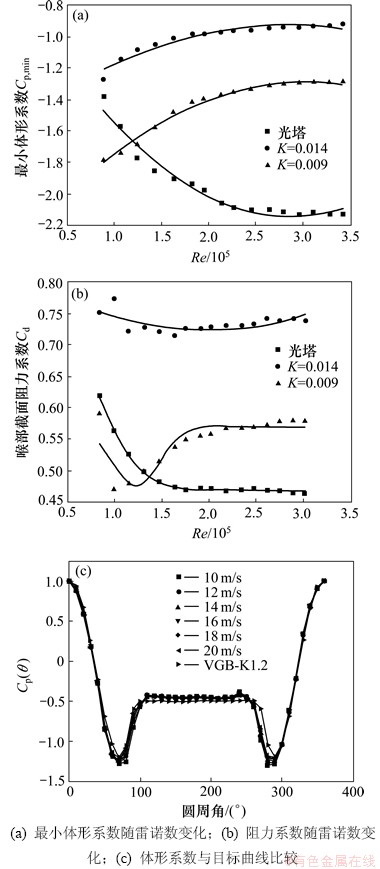
图3 雷诺数效应模拟结果
Fig. 3 Simulation of Reynold’s number effect
同时,群塔最大响应极值可用以下两式表示:
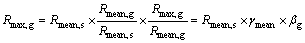 (4)
(4)
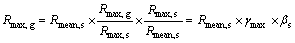 (5)
(5)
式中: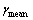 为平均值干扰系数;
为平均值干扰系数; 为极大值干扰系数;
为极大值干扰系数;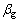 为群体干扰下各工况对应的风振系数;
为群体干扰下各工况对应的风振系数;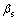 为单塔对应的风振系数。
为单塔对应的风振系数。
由上可知干扰系数可以取均值计算也可以取极大值计算,但风振系数的取值必须与之对应。如若取平均值计算干扰系数,则风振系数必须取群体干扰下各工况对应的风振系数,不同的工况有不同的干扰系数与风振系数。反之,则相应风振系数只需取单塔的风振系数即可,不同的工况有不同的干扰系数但风振系数唯一,即不论何种群体干扰工况,风振系数不变,均为单塔工况下的风振系数。这一点设计时需特别注意,盲目取值可能会使设计偏于保守而增加建设成本。
2.2 荷载干扰系数与响应干扰系数
本文通过POD分解然后插值的办法将36×16= 576个测点测得的风压时程数据扩展为52×108=5 616个点的时程数据,再结合有限元时程分析计算得到不同工况下壳体响应[12-13]。计算结果表明:单塔工况最大径向位移均值为32.54 mm,出现在迎风子午线,高度0.7H(H为塔顶标高)处,群塔布置各风向角下最大值出现位置略有不同,但差别不大,将群塔各风向角的位移最大值与单塔位移最大值相比即为该风向角的位移干扰系数。单塔工况下最大主拉应力均值与最大子午拉应力均值均为1.97 MPa,出现位置也完全相同,均在迎风子午线0.16H高度处;单塔最大子午压应力均值为1.43 MPa,出现位置为最小负压区0.16H位置处,与位移干扰系数计算方法相同可分别求得各风向角下主拉应力及子午应力的干扰系数。将以上按响应求得的干扰系数与按阻力系数求得的干扰系数对比如图4和图5所示。由图4和图5可见:按力系数(阻力系数、合力系数)计算的干扰因子基本接近,按响应(位移、主拉应力等)计算的干扰因子也基本相同,然而按力系数与风压计算得到的干扰因子与按响应计算得到的干扰因子有一定差别,为比较其差别,本文将各风向角下力系数与响应干扰因子分别取均值,然后与按最大正压和最小负压计算得到的干扰因子比较见图6和图7,其中风向角的定义见图8。可以发现最不利风向角即干扰系数最大值往往出现在双塔并列时(W030和W210),而双塔并列时按各方法计算得到的干扰系数差别也较大。
首先,按最大正压计算得到的干扰因子,其值基本在1附近,波动也较响应干扰因子小,其原因可能是最大正压往往受来流动压影响大而受干扰影响小,所以,按最大正压求干扰因子的方法不能直接用于设计。
其次,按最小负压得到的干扰因子其值往往偏大,单塔风压分布曲线直接乘以该系数加载,响应最大值可能大于偏载风压下实际响应的最大值,因此,也不适于指导设计。
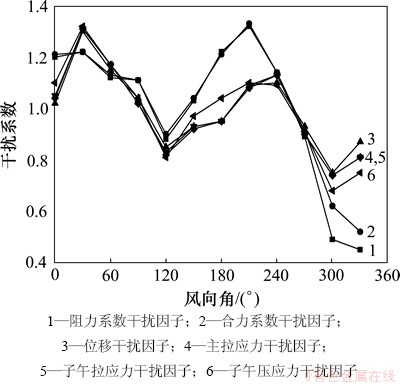
图4 1号塔各风向角下干扰系数图
Fig. 4 Interference factors of tower 1 under different yaw angles

图5 2号塔各风向角下干扰系数图
Fig. 5 Interference factors of tower 2 under different yaw angles
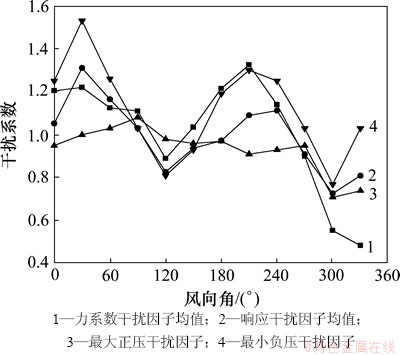
图6 1号塔干扰系数平均值比较
Fig. 6 Compare of average interference factors of tower 1
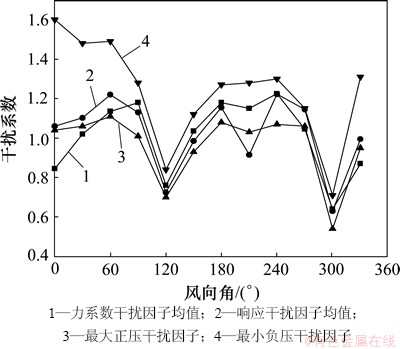
图7 2号塔干扰系数平均值比较
Fig. 7 Compare of average interference factors of tower 2

图8 风向角的定义
Fig. 8 Define of yaw angle
最后,按阻力系数计算得到的干扰因子也与按响应计算得到的干扰因子不同,尤其是在双塔并列时差别最大,说明双塔串列对力系数和响应的干扰效应各不相同。下面通过理论推导分析其原因。
我国DL/T 5339—2006《火力发电厂水工设计规范》[14]中对单塔风压分布曲线定义如式(6)所示。
 (6)
(6)
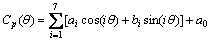 (7)
(7)
式中: 为圆周角
为圆周角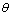 处风压系数;ak,ai,bi和a0为风压系数展开式分项系数;i和k为项数。
处风压系数;ak,ai,bi和a0为风压系数展开式分项系数;i和k为项数。
实践中发现式(6)只适用于拟合单塔工况下风压分布曲线,参照傅里叶级数加上正弦项后(式(7))即可非常好的拟合任何偏载的风压分布曲线,见图9。
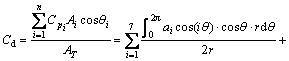
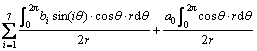 (8)
(8)
其中:
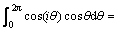
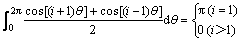
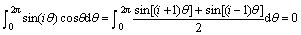

式中:Cpi为第i测点压力系数;Ai为第i测点覆盖面积;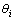 为第i测点压力与风轴方向夹角;AT为i测点所在测层整体结构向风轴方向投影面积;r为i测点所在测层的半径。因此,阻力系数可化简为
为第i测点压力与风轴方向夹角;AT为i测点所在测层整体结构向风轴方向投影面积;r为i测点所在测层的半径。因此,阻力系数可化简为
 (9)
(9)
同理横风向力系数(“升力系数”)可化简为
 (10)
(10)
说明采用阻力系数或“升力系数”求干扰因子,其结果仅是群塔与单塔的风压分布拟合曲线中系数a1或b1的比值,合力系数干扰因子也仅仅与a1和b1相关。为分析风压分布中各项系数对最大响应的贡献,本文将各项系数逐一置1其余置0得到15条由单一项且系数为1构成的风压分布曲线下面称为单位分项系数风压。由风压分布曲线按基本风压和风速剖面求出有限元模型上各层节点对应的风压,而后加风荷载进行静力有限元分析。首先求出按本文测试得到的单塔风压分布曲线下最大响应Xm及其位置Lm,然后按单位分项系数风压分别求解其在Lm位置处的响应分量(Ai,Bi和A0)。
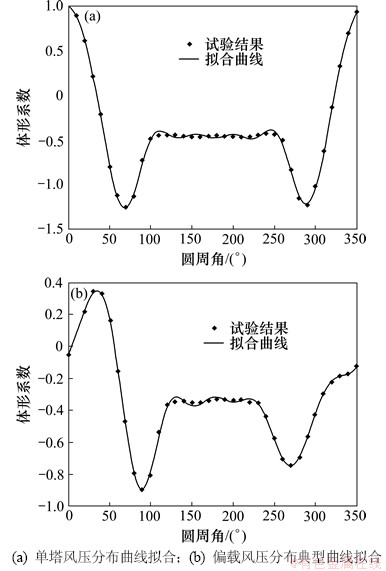
图9 加正弦项拟合风压分布曲线
Fig. 9 Curve fitting of wind pressure distribution by adding sine item
同时可定义各项系数对最大响应的贡献:
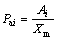 ,
,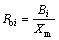 ,
, (11)
(11)
本文仅列径向位移计算结果如表1所示。
由上可知单塔最大响应Xm满足下式:
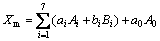 (12)
(12)
将单位分项系数风压对响应贡献汇总如图10所示。由图10可见:系数a1与b1所对应的风压分布对响应的影响并不占主导地位,因此用力系数求得的干扰系数无法准确代表塔体最大响应的干扰系数。
表1 单位分项系数风压分布下径向位移计算结果
Table 1 Results of radial deformation under wind pressure distribution of partial coefficient

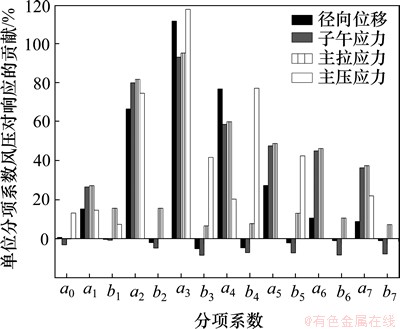
图10 各分项系数风压对单塔响应的贡献率
Fig. 10 Contribution of each partial coefficient of wind pressure to single tower response
为进一步比较荷载干扰系数与响应干扰系数,本文去除地形针对仅双塔干扰进行了刚性模型试验,风向角以串列且干扰塔处下游作为0°,以并列作为90°,以串列且干扰塔处上游为180°,试验结果见图11。由图11可知:各风向角下主拉应力、子午应力及位移的干扰因子吻合较好,其中主拉应力与子午应力干扰因子几乎完全重合,最小负压干扰因子的最大值偏大,而最大正压干扰因子整体偏小,阻力系数干扰因子与响应干扰因子差别最大,与前面得到的结论一致。
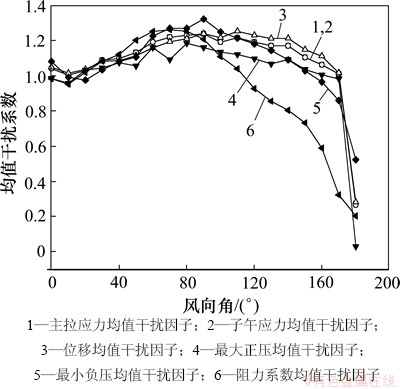
图11 双塔干扰无地形各风向角干扰系数比较
Fig. 11 Compare of interference factor under different yaw angles of double towers
3 结论
1) 计算干扰因子可以取均值计算亦可取极值计算,但风振系数取值必须与之对应:均值干扰因子对应群塔工况风振系数,极值干扰因子对应单塔风振系数。
2) 与响应干扰系数相比最大正压干扰系数往往偏小,最小负压干扰系数往往偏大,其结果均不适于指导设计。
3) 公式推导表明阻力系数或者横风向力系数仅与风压分布拟合曲线中系数a1或者b1相关,而该两项系数所对应的风压对总响应的贡献较小,因此力系数干扰系数不能衡量壳体响应的干扰效应。
4) 按有限元计算得到的响应干扰系数离散型较小,主拉应力干扰系数、主压应力干扰系数、子午应力干扰系数及位移干扰系数基本一致,且能直接反映响应的干扰情况,适于作为冷却塔风荷载干扰系数指导设计。
参考文献:
[1] Harris C L. Influence of neighboring structures on the wind pressure on tall buildings[J]. Journal of Research, 1934, 12: 103-118.
[2] Armitt J. Wind loading on cooling towers[J]. Journal of the Structural Division, ASCE, 1980, 106(ST3): 623-641.
[3] Niemann H J, Kopper H D. Infuluence of adjacent buildings on wind effects on cooling towers[J]. Engineering Structures, 1988, 20: 874-880.
[4] Orlando M. Wind-induced interference effects on two adjacent cooling towers[J]. Engineering Structures, 2001, 23: 979-992.
[5] 顾志福, 孙天风, 季书弟. 沙岭子电厂冷却塔群风荷载的风洞研究[J]. 力学学报, 1992, 24(2): 129-135.
GU Zhifu, SUN Tianfeng, JI Shudi. A wind-tunnel study of wind loading on cooling towers of Shalinzi power station[J]. Acta Mechanica Sinica, 1992, 24(2): 129-135.
[6] 张军峰, 赵林, 柯世堂, 等. 大型冷却塔双塔组合表面风压干扰效应试验[J]. 哈尔滨工业大学学报, 2011, 43(4): 81-87.
ZHANG Junfeng, ZHAO Lin, KE Shitang, et al. Wind tunnel investigation on wind-pressure interference effects for two large hyperboloidal cooling towers[J]. Journal of Harbin Institute of Technology, 2011, 43(4): 81-87.
[7] 沈国辉, 刘若斐, 孙炳楠. 双塔情况下冷却塔风荷载的数值模拟[J]. 浙江大学学报(工学版), 2007, 41(6): 1017-1022.
SHEN Guohui, LIU Ruofei, SUN Binnan. Numerical simulation of wind load on cooling towers under double tower condition[J]. Journal of Zhejiang University (Engineering Science), 2007, 41(6): 1017-1022.
[8] 沈国辉, 余关鹏, 孙炳楠, 等. 大型冷却塔双塔干扰的风洞试验研究[J]. 振动与冲击, 2011, 30(3): 109-114.
SHEN Guohui, YU Guangpeng, SUN Binnan, et al. Study on interference effects of two large hyperbolic cooling towers by using wind tunnel test[J]. Journal of Vibration and Shock, 2011, 30(3): 109-114.
[9] VGB-R 610Ue: 2005, Structural design of cooling towers[S].
[10] 王峰峰, 赵林, 曹曙阳, 等. 紊流积分尺度实用识别算法及其数值验证[J]. 建筑科学与工程学报, 2012, 29(4): 67-73.
WANG Fengfeng, ZHAO Lin, CAO Shuyang, et al. Practical recognition algorithm of turbulence integral scale and its numerical validation[J]. Journal of Architecture and Civil Engineering, 2012, 29(4): 67-73.
[11] 刘天成, 赵林, 丁志斌. 圆形截面冷却塔不同表面粗糙度时绕流特性的试验研究[J]. 工业建筑, 2006, 36(增刊1): 301-304.
LIU Tiancheng, ZHAO Lin, DING Zhibin. Test research of flow feature for hyperbolic circular section cooling tower with different superfacial roughness[J]. Industrial Construction, 2006, 36(S1): 301-304.
[12] 李方慧, 倪振华, 沈世钊. POD方法在双坡屋盖风压场预测中的应用[J]. 工程力学, 2007, 24(2): 68-73.
LI Fanghui, NI Zhenhua, SHEN Shizhao. Application of POD to prediction of wind pressure fields of pitched roof[J]. Engineering Mechanics, 2007, 24(2): 68-73.
[13] 鲍侃袁. 大型双曲冷却塔的风荷载和风致响应理论分析与试验研究[D]. 浙江: 浙江大学建筑工程学院, 2009: 161-173.
BAO Kanyuan, Theoretical analysis and experimental research of wind load and wind-induced response of a large hyperbolic cooling tower[D]. Zhejiang: Zhejiang University. College of Civil Engineering and Architecture, 2009: 161-173.
[14] DL/T 5339—2006, 火力发电厂水工设计规范[S].
DL/T 5339—2006, Technical specification for hydraulic design of thermal power plant[S].
(编辑 杨幼平)
收稿日期:2013-09-17;修回日期:2013-12-29
基金项目(Foundation item):国家自然科学青年基金资助项目(50908085);国家自然科学基金重大资助项目(91215302) (Project(50908085) supported by National Natural Science Youth Foundation of China; Project(91215302) supported by Major Program of National Natural Science Foundation of China)
通信作者:牛华伟(1978-),男,河南驻马店人,博士,硕士生导师,从事结构抗风研究;电话:13787103586;E-mail: niuhw@hnu.edu.cn