瑞雷波数值模拟中的边界条件及模拟实例分析

熊章强¹，张大洲²，秦  臻²，周文斌¹

(1. 中南大学 信息物理工程学院，湖南 长沙，410083；

2. 中国地质大学 地球物理与空间信息学院，湖北 武汉，430074)

摘  要：应用_2×2阶高精度交错网格有限差分法，建立震源位于地表时瑞雷波数值模拟的自由边界条件；同时，采用PML吸收边界条件以消除模拟时的边界反射。通过对均匀各向同性介质及2层介质模型的计算，验证所采用的自由边界条件和吸收边界条件的有效性及波场模拟的正确性。研究结果表明：模拟结果与解析结果相对误差在5%以内，并指出在同一精度下通过提高差分阶数比减少网格间距所需计算时间少。在2层介质模拟的基础上，对含有软弱夹层的3层介质进行模拟，得到更加接近实际情况的地震记录，频散曲线产生多个模式，并出现“之”字型回折。

关键词：瑞雷波；高阶有限差分；边界条件；波场特征

中图分类号：P631         文献标识码：A         文章编号：1672-7207(2008)04-0824-07

Boundary conditions and case analysis of

numerical modeling of Rayleigh wave

XIONG Zhang-qiang¹, ZHANG Da-zhou², QIN Zheng², ZHOU Wen-bin¹

(1. School of Info-Physics and Geomatics Engineering, Central South University, Changsha 410083, China;

2. Institute of Geophysics and Geomatics, China University of Geosciences, Wuhan 430074, China)

Abstract: A free surface boundary condition for numerical simulation of Rayleigh wave was built by using _2×2 order high precision staggered grids finite difference when the source was at the free surface. PML absorbing boundary condition was applied to eliminate boundary reflections. Wave-field modeling of homogeneous isotropic medium and two layer models prove the effectiveness and correctness of using the free surface boundary condition and absorbing boundary condition. The results of model simulating show that relative error between numerical and analytic solutions is within 5%. At the same accurate level, improving difference order has less computation time compared to decreasing grids space. On the base of two-layer model, a seismic record is gotten more practically from modeling the soft interlayer model. The dispersion curve of seismic record has many modes and exhibits the shape of zigzag of reversing phenomena.

Key words: Rayleigh wave; high-order finite difference; boundary conditions; wave-field characteristics

瑞雷波勘探是近年来迅速发展的一种工程地球物理勘探方法。一些学者对瑞雷波的传播理论进行了大量的研究工作，但主要集中在频散曲线的正反演方面^[1-2]。利用瑞雷波频散方程只能对一些简单的层状介质进行正演，对复杂的地质结构无法用瑞雷方程得到其正演结果，而只能采用数值模拟方法^[3]。在瑞雷波数值模拟方面，周竹生等^[4]用有限差分法进行了模拟，但在其均匀半空间模型中所模拟的波场出现了明显的频散现象，模拟精度较低和边界条件没处理好是其重要原因。XU等^[5]采用AEA法对自由边界进行处理，得到了较好的效果。但由于采用空间2阶差分精度，在满足精度要求时必须增大最小波长中的网格数，即减小网格间距，这样势必会大量增加计算时间。Bohlen^[6]对普通交错网格和旋转交错网格进行了讨论。讨论结果表明，由于采用的差分阶数较低，要达到一定的计算精度同样需要增加最小波长中的网格数。此外，有些在采用高阶差分计算时由于自由边界处理的复杂性，在自由边界采用降阶的方式。采用这种方法对于瑞雷波模拟的计算精度有一定的影响，因此，在瑞雷波数值模拟时采用高精度有限差分的研究具有非常重要的意义。此外，有限的空间区域模型边缘产生的虚假反射，严重干扰了有效波信息，并影响了对瑞雷波传播规律及频散特征的正确认识。所以，确定一种好的吸收边界是瑞雷波模拟成功的关键因素之一。

在此，本文作者通过研究交错网格高阶有限差分模拟瑞雷波时的自由边界条件和吸收边界条件，用模型实例模拟得到震源位于自由界面时的瑞雷波波场，并对波场特征进行分析和解释。

1  波动方程的交错网格高阶有限差分

在二维均匀各向同性弹性介质中，一阶速度-应力标量弹性波动方程为^[7]：

设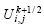，，，和分别为速度v_x，v_z与应力τ_xx，τ_zz和τ_xz的离散

值。应用交错网格有限差分法求解方程(1)，可得精度为的差分格式，其他4个方程的差分格式与此类似。差分所采用的网格剖分方案如图1所示。

图1  交错差分网格模型

Fig.1  Model of staggered finite-difference grid

空间网格尺寸和时间间隔的选择在瑞雷波模型计算中是十分重要的，为了保证计算精度和兼顾计算效率，对于阶的差分精度，取 Δ_x≤和_Δt≤^[8]。其中v_max和λ_min分别为模型中最大速度和最短波长。

2  边界条件

2.1  自由边界

进行弹性波数值模拟时，不同研究者对自由边界条件进行了不同的处理。Mittet^[9]将v_x，τ_xx和τ_zz置于自由界面采样，震源置于界面以下10 m，且ρ(i, 0)= ρ(i, 1)/2，μ(i, 0)= μ(i, 1)/2和λ(i, 0)=0，其中(i, 0)和(i, 1)分别表示界面网格节点和低于界面以下1个网格的节点。裴正林^[10] 在自由边界定为四阶差分精度，其余网格定为十阶差分精度，采用镜像加零速度法，将v_x，τ_xx和τ_zz在自由界面采样，界面以上的2层质点速度v_x和v_z为0，τ_xz和τ_zz镜像对称，即τ_xz(i, -1/2)= τ_xz(i, 1/2)，τ_zz(i, -1)= τ_zz(i, 1)，τ_zz(i, 0)=0。WANG等^[11]采用四阶差分精度并将v_z和τ_xz置于自由界面采样，界面以上采用镜像法。以上3种自由边界的处理或将震源置于自由界面以下，或在自由边界采用降阶处理。本文采用空间12阶差分精度，在界面以上设置6层真空层(弹性参数为0)，同时，将v_z和τ_xz置于自由界面采样，v_x，τ_xx和τ_zz在界面下采样。通过这样的设置可使自由界面处理相对简单，在界面上只需考虑τ_zz和τ_xz，而不需考虑τ_xx。在界面上正应力τ_zz和剪切应力τ_xz应等于0，可令τ_xz(i, 0)=0。垂直速度分量v_z在计算时只涉及密度ρ，而ρ(i, 0)=[ρ(i, -1)+ρ(i, 1)]/2，由于界面以上为真空，可知ρ(i, -1)=0，因此，ρ(i, 0)= ρ(i, 1)/2。当ρ(i, 0)= ρ(i, 1)/2时，自由界面存在一反射界面，从而使得球面波在界面反射产生瑞雷波。在界面上，τ_xz=0，即H_{(i, 0)}=0，则U为：

由于在自由界面以上速度分量和应力分量均为0，故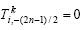，式(3)变为

将式(4)进行变换得到：

则自由界面处T分量

的高阶一次差分算子在长度上关于z=0反对称。这样同样达到了虚像法的目的，满足了τ_zz在自由界面上等于0的条件。

2.2  吸收边界

计算吸收边界的方法有多种^[12]，如指数衰减法和基于波动方程旁轴近似法。虽然旁轴近似法实现较简单且需要的网格数较少，能完全吸收垂直入射的反射波，但这只在一定角度和频率范围内有效吸收，且该方法对于面波的吸收效果不好。Berenger^[13-14]提出的完全匹配层(PML)吸收边界条件是：将弹性波分量在吸收边界区分裂，并分别对各个分裂的波场分量赋以不同的损耗。这样，能在计算区域截断边界处得到一种非物理的特殊吸收介质，该层介质的波阻抗与相邻介质的波阻抗完全匹配，因而，入射波将无反射地穿过分界面而进入PML层。由于PML层为有耗介质，故进入PML层的入射波将迅速衰减。图2所示为PML法吸收边界示意图。

图2  PML吸收边界示意图

Fig.2  Schematic diagram of PML absorbing boundary

在进行波场模拟时，PML介质中5个分量中的每个分量分别被分裂为2个，它们分别为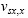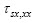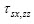：，，，，，，，和。这些波场分量满足以下方程：

2.3  边界处理效果分析

为了验证自由边界采用高阶差分格式的正确性和计算时间上的优势，设计一均匀各向同性介质模型。模型参数如下：模型长×宽为100 m×80 m，纵波速度vp=1 km/s，横波速度vs=200 m/s，密度ρ=1.7 g/cm3；中心频率f=25 Hz，震源置于左边自由边界(0,0)处。左边界吸收层厚度L=15个网格点，右边界和底边界吸收层厚度L=10个网格点。将高阶差分计算得到的结果与理论解以及Xu等[5]采用AEA方法所得结果进行对比。高阶差分采用(2，12)阶，1个最小波长上有8个网格；AEA方法采用(2，2)阶差分，1个最小波长上有32个网格。图3所示为采用这2种方法在偏移距为30 m时的计算结果和理论解对比。可以看出，采用这2种方法所得结果都与理论解较吻合。采用相同参数时的不同差分格式(本文所采用的自由边界条件对于低阶差分同样使用)以及不同参数下的相同差分格式2种情况下对计算时间进行对比，对比结果见表1。从表1可以看出：采用PⅣ2.8G计算机进行计算，对于参数相同时(2，12)阶差分格式计算时间为85 s，(2，2)阶计算时间为55 s，差分阶数提高6倍，计算时间增加0.55倍。当差分格式都采用(2，2)阶时，1个最小波长中所占的网格数由8增加到32，网格数增加4倍，但计算时间增加44倍。由此可见，在达到同一精度的情况下，提高差分阶数比减少网格间距所花费的时间少得多，因而具有明显的优势。

图3  2种模拟解和理论解地震记录垂直分量对比

Fig.3  Comparison of seismograms of vertical particle velocity between analytical and numerical results

表1  不同参数下计算时间对比

Table 1  Comparison of time with different parameters

为便于对吸收边界条件的有效性进行对比分析，分无吸收边界和加PML吸收边界2种情况讨论。这2种情况均采用同一厚度的人工边界。图4所示为未加任何人工边界条件时的波场快照，可见，边界反射(周期折叠效应)特别强烈，尤其是右边界反射的横波和面波，这些波形成严重的干扰，直接影响计算的波场记录特征。

图4　未加吸收边界时的波场快照

Fig.4  Snapshot without absorbing boundary

图5所示为采用PML吸收边界条件时的瑞雷波波场快照。可见，加了PML吸收边界以后，由于该边界条件很好地消除了周期折叠效应，大大削弱了人工边界的反射，反射的横波、面波及纵波几乎全部被吸收，使得所要计算的波场特征变得非常清晰，横波和瑞雷波清楚地显示在波形记录上。经计算，PML吸收边界条件的吸收率(吸收能量与未吸收能量之比)为99.99%，可见，使用PML，可以使FDTD模拟的最大动态范围达到80 dB。

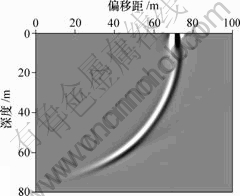
图5　加PML吸收边界时的波场快照

Fig.5  Snapshot of PML absorbing boundary

3　数值模拟算例

3.1  2层介质模型

设计1个二层介质模型，模型长×宽为110 m×80 m。模型介质参数为：第1层厚度h=10 m，纵波速度v_p=1 km/s，横波速度v_s=250 m/s，密度ρ=1.8 g/cm³；第2层纵波速度v_p=1.5 km/s，横波速度v_s=500 m/s，密度ρ=2.0 g/cm³。取空间网格间距?x=?z=0.4 m，时间步长?t=0.1 ms，为了减小边界吸收效应，震源位于地表(-10, 0)处，所用高斯一阶导数子波主频为20 Hz。图6所示为模拟后的瑞雷波波场单炮记录，从图6可看出瑞雷波的位置以及直达波、横波、反射波等。

图6  2层介质模型单炮记录

Fig.6  Single-shot records for two layer models

图7所示为对波场记录采用相移法^[15]得到的频散曲线，虚线为其解析解。可见，沿2层介质传播的瑞雷波出现了多个模式，从低到高分别称为第1、第2、第3阶模式，第1阶模式为基阶模式，第2、第3阶等为高阶模式。基阶模式无截止频率，相速度0频极限为500 m/s，为只有第2层介质时的瑞雷波速度；而其他诸模式都具有截止频率，在截止频率处的相速度均接近于第2层介质的横波速度(500 m/s)；所有模式的高频速度均趋向于第1层的横波速度(250 m/s)。为了验证数值模拟的正确性及计算精度，将模拟得到的频散曲线与瑞雷波频散方程的解析解进行比较，结果见表2。从表2可知，从基阶到第4阶模式瑞雷波，相对误差最大为4.35%，最小为0.58%，模拟解与解析解较吻合。

图 7  2层介质模型频散曲线

Fig.7  Dispersion curves of Rayleigh wave in

 two layer models

表2  有限差分模拟解与解析解相速度比较

Table 2  Phase velocity comparison between FD-modeling results and analytical results

3.2  软弱夹层模型

为了模拟实际地层中的软弱夹层结构，设计1个3层固体介质模型。其中：第1层介质的纵、横波速度分别为：v_P1=450 m/s，v_S1=150 m/s，密度ρ₁=1.9 g/cm³，厚度h₁=3 m；第2层介质的纵、横波速度分别为：v_P2=300 m/s，v_S2=100 m/s，密度ρ₂=1.8 g/cm³，厚度h₂=2 m；第3层介质的纵、横波速度分别为：v_P3=700 m/s，v_S3=225 m/s，密度ρ₃=2.0 g/cm³。空间网格间距?x=?z=0.2 m，时间步长?t=0.1 ms，震源位于地表(0, 0)处，所用高斯一阶导数子波主频为25 Hz。

图8所示为软弱夹层模型的单炮记录，可明显看出瑞雷波发生频散，并大致可算出瑞雷波的相速度为120~180 m/s。图9所示为对波场记录采用相移法^[15]得到的频散曲线，可见，频散曲线出现了多个模式。若进一步将频率换算成瑞雷波的半波长，则在频散曲线中出现了“之”字型回折，如图10所示，这种结果与野外的实际勘探结果非常接近。但在目前的瑞雷波勘探中，人们对在同一个频率下可能会激发出多个模式的瑞雷波并不完全了解，进行资料处理时大多采用基阶模式进行反演解释，所得结果显然与实际结果产生较大误差。

图8  软弱夹层模型单炮记录

Fig.8  Single records of floppy interlayer model

图9  软弱夹层模型的频散曲线

Fig.9  Dispersion curves of floppy interlayer model

图10  由多阶瑞雷波组成的“之”字型回折

Fig.10  Zigzag curve made up of various modes

Rayleigh wave

4　结  论

a. 建立了震源位于自由界面时高阶有限差分模拟瑞雷波的自由边界条件及PML吸收边界条件。对均匀各向同性介质模型数值的模拟结果表明，利用一阶速度－应力弹性波方程在计算域内采用高阶交错网格有限差分法，可正确地模拟瑞雷波波场，运算效率也得到很大提高。

b. 通过对2层介质和含软弱夹层的3层介质模型的模拟，在波场记录上可清晰看到瑞雷波，其频散曲线具有高阶模式特征，模拟所得频散结果与理论频散结果相对误差在5%以内。3层介质出现“之”字型回折，与野外的实际勘探结果非常接近。这对进一步模拟其他复杂介质中瑞雷波传播特征和研究其传播规律具有重要意义。

参考文献：

[1] 张碧星, 肖柏勋, 杨文杰. 瑞利波勘探中“之”字型频散曲线的形成机理及反演研究[J]. 地球物理学报, 2000, 43(4): 557-567.
ZHANG Bi-xin, XIAO Bo-xun, YANG Wen-jie. Mechanism of zigzag dispersion curves in Raleigh wave exploration and its inversion study[J]. China Journal Geophysics, 2000, 43(4): 557-567.

[2] 肖柏勋. 高模式瑞雷面波及其正反演研究[D]. 长沙: 中南大学信息物理工程学院, 2000.
XIAO Bo-xun. High mode Rayleigh wave and forward and inversion of its dispersion curves[D]. Changsha: School of Info-Physics and Geomatics Engineering, Central South University, 2000.

[3] 熊章强. 复杂介质中瑞雷面波的正演模拟及传播特征研究[D]. 武汉: 中国地质大学地球物理与空间信息学院, 2006.
XIONG Zhang-qiang. A study on forward modeling and propagation characteristics of Rayleigh wave in complex mediums[D]. Wuhan: Institute of Geophysics and Geomatics, China University of Geosciences, 2006.

[4] 周竹生, 刘喜亮, 熊孝雨. 弹性介质中瑞雷面波有限差分法正演模拟[J]. 地球物理学报, 2007, 50(2): 567-573.
ZHOU Zhu-sheng, LIU Xi-liang, XIONG Xiao-yu. Finite difference modeling of Rayleigh surface wave in elastic media[J]. China Journal Geophysics, 2007, 50(2): 567-573.

[5] XU Yi-xian, XIA Jiang-hai, Miller R D. Numerical investigation of implementation of air-earth boundary by acoustic-elastic boundary approach[J]. Geophisic, 2007, 72(5): P.SM147- P.SM153.

[6] Bohlen S R. Accuracy of heterogeneous staggered-gridfinite- difference modeling of Rayleigh waves[J]. Geophysics, 2006, 71(4): P.T109- P.T115.

[7] 董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419.
DONG Liang-guo, MA Zai-tian, CAO Jin-zhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. China Journal Geophysics, 2000, 43(3): 411-419.

[8] Virieax J. P-SV wave propagation in heterogeneous media: Velocity-stress finite-difference method[J]. Geophysics, 1986, 51(4): 889-901.

[9] Mittet R, Free-surface boundary conditions for elastic staggered-grid modeling schemes[J]. Geophysics, 2002, 67(5): 1616-1623.

[10] 裴正林. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油地球物理勘探, 2004, 39(6): 629-634.
PEI Zheng-lin. Numerical modeling using staggered-grid high order finite-difference of elastic wave equation on arbitrary relief surface[J]. OGP, 2004, 39(6): 629-634.

[11] WANG Xiu-ming, ZHANG Hai-lan. Modeling of elastic wave propagation on a curved free surface using an improved finite-difference algorithm[J]. Science in China, 2004, 5: 633-648.

[12] Dai N, Vafidis A, Kanasewich E. Composite absorbing boundaries for the numerical simulation of seismic waves[J]. Bull Seis Soc Am, 1994, 84(1): 185-191.

[13] Berenger J P. A perfectly match layer for the absorption of electromagnetic waves[J]. Journal of Computation Physics, 1994, 114: 185-200.

[14] Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2003, 68(5): 1749-1755.

[15] Park C B, Miller R D, Xia J. Imaging dispersion curves of surface waves on multi-channel record[C]//68th Annual International Meeting, SEG, Expanded Abstracts. 1998: 1377-1380.

收稿日期：2007-10-31；修回日期：2008-03-08

基金项目：“十一五”国家科技支撑项目(2006BAC07B00)；江西省自然科学基金资助项目(05560003)

通信作者：熊章强(1963-)，男，湖南宁乡人，教授，博士，从事地震勘探及工程地球物理的教学和科研工作；电话：0731-8830451；E-mail: ycxzq@mail.csu.edu.cn.