变环境变工作条件下电子系统的可靠性评价方法
覃庆努,魏学业,黄赞武,孟一飞
(北京交通大学 电子信息工程学院,北京,100044)
摘要:为对变环境变工作条件下电子系统的可靠性进行有效评价,提出一种基于受控赋时混合随机Petri网(CTHSPN)的电子系统可靠性评价方法。首先,在混合随机Petri网的基础上将库所标识扩展到云域并与时间关联、引入控制函数和控制时钟,提出CTHSPN模型;其次,根据CTHSPN模型的建模机制建立电子产品的可靠性模型;最后,在产品可靠性模型的基础上,根据电子系统的失效机制和部件间的动态关系建立系统的可靠性模型,并通过Monte Carlo模型仿真计算出系统可靠度。实例分析表明:该方法能较好地体现温度、电压等工作条件对电子系统可靠性的独立性影响作用,为变环境变工作条件下电子系统的可靠性评价提供一条有效的途径。
关键词:可靠性评价;云模型;受控赋时混合随机Petri网;环境条件
中图分类号:TN60;TB114 文献标志码:A 文章编号:1672-7207(2013)08-3254-07
Reliability evaluation method of electronic system under variable environments and working conditions
QIN Qingnu, WEI Xueye, HUANG Zanwu, MENG Yifei
(School of Electronic and Information Engineering, Beijing Jiaotong University, Beijing 100044, China)
Abstract: To study the influence of the variation of environments and working conditions on the reliability of electronic system, a system reliability evaluation method based on controlled time hybrid stochastic Petri net (CTHSPN) was proposed. Firstly, by extending the place’s field to cloud field and associating it with time, inducing control function and control clock on the basis of hybrid stochastic Petri net, CTHSPN model was proposed. Secondly, the component’s reliability model based on CTHSPN was established. Finally, the system’s reliability model was established according to system’s failure mechanism and components’ dynamic relationship, and the system’s reliability was calculated by Monte Carlo method. The given example shows that the proposed method well reflects the working conditions’ independent influence on the system’s reliability, and provides an effective way to evaluate the reliability of electronic system under variable environments and variable working conditions.
Key words: reliability evaluation; cloud model; controlled timed hybrid stochastic Petri net; environment factor
可靠性通常定义为产品在规定的工作条件下,规定的时间内,完成规定功能的能力[1]。传统的可靠性评价方法里,规定的工作条件一般限定为一个或几个典型的不变的条件。实际中的产品多处于可变的、不确定的工作条件中,大量研究已经表明,工作条件的这种变化会对产品的可靠性产生不同程度的影响[2-4],而传统的可靠性评价方法难以描述工作条件变化对系统可靠性的影响,这就使得根据传统的可靠性评价方法得到的可靠性指标与实际情况相脱离。20世纪末,李德毅[5]在概率论和模糊数学理论交互的基础上,提出了以云模型为核心的云理论,把模糊性和随机性有机的集成到一起,为科学研究中不确定性问题的处理提供一条有效的途径。迄今为止,云理论已经发展成为一套比较完整的理论[6],在众多领域得到很好的应用。宋远骏等[7-8]最早将云理论引入可靠性领域,通过建立产品的环境适应能力模型和工作条件模型,提出可变工作条件下单个电子产品和计算机类产品的可靠性评价方法。但如何利用云模型进行整个系统的可靠性建模和评价、反映系统部件之间的关系和系统的动态行为,并未得到解决。Fu等[9]采用可靠性框图建模法,利用云模型对可变工作条件下串并联系统的可靠性进行了研究;Shao等[10]采用故障树建模法,结合云模型对可变工作条件下自动监测系统的可靠性进行评价;原菊梅等[11]结合云模型,提出了一种受控混合随机Petri网(CHSPN),利用连续库所中的托肯控制离散变迁的变迁率,反映工作条件变化对部件可靠性的影响,对可变工作条件下分布式系统进行可靠性建模和分析。而工作条件的变化规律或情况与系统所处的环境有关,不同的环境下,工作条件的变化规律或情况会有很大的差别。Fu等[9-11]的方法描述的实际上是某固定环境下工作条件变化对系统可靠性的影响,对于系统需经历多种环境的情况(如远距离运行的火车,其所处环境会随着火车的运行而改变,工作条件变化规律也随着环境的不同而不同,本文称为“变环境变工作条件”),其难以进行分析和评价。本文作者通过将云模型和Petri网相结合,提出一种受控赋时混合随机Petri网(CTHSPN)模型,并在此基础上形成一种基于CTHSPN的电子系统可靠性评价方法,以解决变环境变工作条件下电子系统的可靠性评价问题。
1 云理论
1.1 云的定义及数字特征[6]
设U是一个用精确数值表示的定量论域,C是U上的定性概念,若定量值x∈U,且x是定性概念C的1次随机实现,x对C的确定度μ(x)∈[0,1]是有稳定倾向的随机数,即μ:U→[0,1]  x∈U x→μ(x)。则x在论域U上的分布称为云,每1个x称为1个云滴。
x∈U x→μ(x)。则x在论域U上的分布称为云,每1个x称为1个云滴。
云的数字特征用期望Ex,熵En和超熵He 3个数值表示,如图1所示。
(1) 期望Ex。是在论域空间中最能够代表定性概念的点,反映了代表此定性概念的云滴群的重心。
(2) 熵En。定性概念的不确定性度量,由概念的随机性和模糊性共同决定,反映随机性和模糊性之间的关联性。
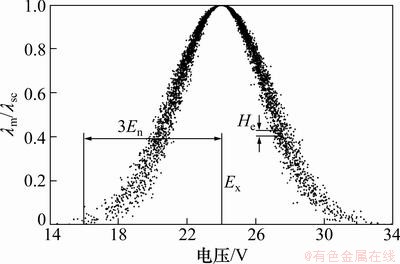
图1 云及其数字特征
Fig. 1 Cloud and its numerical characteristics
(3) 超熵He。熵的不确定性度量,即熵的熵,反映熵的离散程度。
1.2 云发生器[6]
根据云产生的机理和方向,云发生器(CG)可分为正向、逆向和X条件云发生器等,如图2所示。
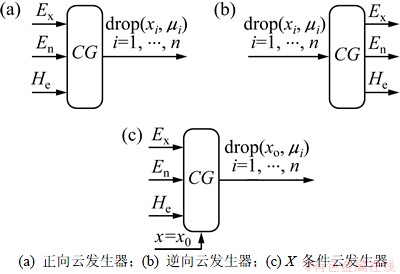
图2 云发生器
Fig. 2 Cloud generators
(1) 正向云发生器。给定云的3个数字特征Ex,En和He,产生满足上述特征的正态云分布规律的二维点drop(xi, μi)(即云滴)。
(2) 逆向云发生器。给定若干个符合正态云分布规律的云滴样本drop(xi, μi),产生云的3个数字特征。
(3) X条件云发生器。给定云的3个数字特征和特定x值x=x0,产生满足上述条件的云滴drop(x0, μi)。
各种云的生成算法可参见文献[6]。
1.3 环境适应能力模型[7-8]
所有电子产品都有其环境条件适应范围,环境条件的变化会导致产品失效率的变化。一般而言,产品在理想环境条件下失效率最低(通常生产厂家给出的标称失效率都是在理想条件下测得),偏离理想条件越远,失效率越高,超出适应范围,产品无法工作。由此,可采用一维正态云来描述单个环境条件变化对产品失效率的影响,称之为适应云,即:
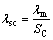 (1)
(1)
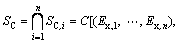
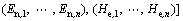 (2)
(2)
其中:λsc为失效率适应云;λm为厂家给出的标称失效率;SC为n维环境条件适应云;SC,i为产品对第i项环境条件的适应云。若已知产品在不同条件下的失效率测试数据,适应云的数字特征Ex,En和He可以由文献[7]的逆向云发生器法给出;若只知产品的环境适应范围时,Ex,En和He可以由文献[7]的指标近似法给出。图1描述的即是标称电压为24 V、电压适应范围为16~32 V的产品对电压条件的失效率适应云。
1.4 工作条件模型[7-8]
工作条件模型是产品在实际工作时,所处环境条件情况的描述,所处环境不同,工作条件模型也将不同。在工作条件可变时,如何对工作条件进行定量描述是一个难题。如果工作条件的变化有较为准确的变化规律,可采用已有的经验公式或模型来进行描述,例如原菊梅等[11]给出的电压、气温等的经验公式。但很多时候,工作条件的变化并不确定,没有准确的变化规律,通常只能以数值范围或者定性语言表示。在此,运用云模型来描述此类变化的工作条件:
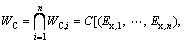
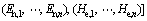 (3)
(3)
其中:WC为n维工作条件云;WC,i为第i项环境条件的云表达式。工作条件云的横坐标为某项环境条件的具体数值表示(例如电压为24 V,温度为20 ℃等,在此称之为具体条件),纵坐标为某一具体条件对定性工作条件的隶属度,体现该具体条件出现的频率或时长。数值范围表示的工作条件,其云模型的数字特征可由指标近似法给出;定性语言表示的工作条件,其云模型的数字特征由人们的常识和对工作条件的认识程度给出。得出工作条件云模型后,可由正向云发生器还原出该工作条件下的若干个具体条件。
适应能力模型给出某一具体条件下产品失效率,工作条件模型给出变化工作条件下具体条件的出现情况,将实际工作条件作为X条件,通过X条件云发生器可得到变化工作条件下的失效率云λwc,即
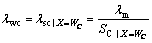 (4)
(4)
2 CTHSPN及其可靠性建模
Petri网作为研究动态系统的一种有力工具被广泛应用于可靠性领域[12],根据各类系统的特点,各种改进的Petri网模型不断被提出并用于系统的可靠性分析和评价,例如广义随机Petri网[13](GSPN)、模糊神经Petri网[14](FNPN)、流体随机Petri网(FSPN)[15]等。而如何采用Petri网对变环境变工作条件下电子系统的可靠性进行研究仍是一个难题,因此,提出一种受控赋时混合随机Petri网(CTHSPN)以解决此问题(图3)。
2.1 定义
一个受控赋时混合随机Petri网定义为七元组,即:fCTHSPN=(P,T,F,M,W,O,f),其中:
(1) P=Pd∪Pc是库所的有限集合。Pd为离散库所,图3中用○表示;Pc为连续库所,图3中用◎表示。
(2) T=Td∪Tc是变迁的有限集合。Td为离散随机变迁,图3中用│表示;Tc为连续变迁,图3中用┃表示。Td从使能到实施需要一定时延,并且此时延服从参数为λ的指数分布。Tc使能后瞬时实施。
(3) 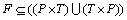 为库所与变迁之间的有向弧的集合。
为库所与变迁之间的有向弧的集合。
(4) M为系统的标识函数,与时间τ相关。M(P,τ)表示τ时刻库所P里的标记值。当P为离散库所时,M(P,τ):P→N;当P为连续库所时,M(P,τ) :P→ R+∪U,其中,U表示云集。
(5) W:F→R+∪U为弧权函数。变迁使能后从其输入库所消耗或读取输入弧弧权大小的标记,实施后生成输出弧弧权大小的标记并输出至输出库所。
(6) O为变迁的控制时钟,用以触发控制作用。第一级变迁的时钟根据环境的变化和实际工作条件变化情况给出;第一级以后变迁的时钟由上一级变迁的时钟经过叠加、组合得到。
(7) f为变迁的控制函数,以该变迁的输入弧权为自变量。变迁为连续变迁时,f决定其输出弧权;变迁为离散随机变迁时,f决定其实施速率,即λ。在下次控制作用发生前,λ保持当前值不变。
(8) 对于连续变迁,其所有输入库所中的标记值大于等于其输入弧的弧权值且控制时钟被触发时,变迁使能。连续变迁的使能只能读取其输入库所中的标记,但不能改变输入库所中的标记值。
(9) 对于离散变迁,当其所有离散输入库所中的标记值大于等于其输入弧的弧权值时,变迁使能。离散变迁使能后将消耗其输入库所中的标记。控制时钟和连续输入库所对离散变迁的使能没有影响,但会影响离散变迁的实施。在离散变迁使能到实施的过程中,其控制时钟每触发1次,则变迁消耗其连续库所的标记1次,变迁实施速率λ根据f改变1次。
2.2 基于CTHSPN的电子产品可靠性模型
根据CTHSPN的定义,可得变环境变工作条件下电子产品的可靠性模型,如图3所示。
图3中:库所Ps,i代表产品对第i项环境条件的适应能力;Pw,i代表实际的工作条件情况;Psw,i代表该工作条件下,第i项环境条件对产品失效率的影响因子;Psw代表该工作条件下,所有环境条件对产品失效率的综合影响因子;Pg表示产品工作状态;Pf表示其失效状态。
变迁采用(t,O)的形式描述,图3中t1~tn为第一级变迁,tn+1为第二级变迁,tn+2为第三级变迁。第一级变迁的控制时钟由环境划分和该环境下的实际工作条件情况决定,同一环境内,控制时钟的触发可根据该环境下的工作条件变化情况确定。第二级以后变迁的时钟由变迁的性质和相关的上一级变迁时钟共同决定。图3中,由于变迁t1~tn+1均为瞬时变迁,可知On+1由O1~On+1直接叠加而成,而On+2等于On+1。
标识函数M(P)代表库所P里的标记值,其在图3中作为弧权函数,表示变迁使能或控制作用发生时将从库所P里读取或消耗当前的标记值。
图3中控制函数f1~ fn+1用以控制相应变迁的输出弧权;fn+2用以控制变迁tn+2的实施速率。各控制函数的表达形式如下:
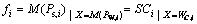
(i=1,2,…,n) (5)
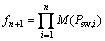 (6)
(6)
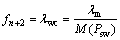 (7)
(7)
2.3 基于CTHSPN的电子系统可靠性评价方法
由2.2节可对变环境变工作条件下电子系统的可靠性进行评价,步骤如下。
(1) 根据系统工作情况,确定会对系统可靠性产生影响的环境条件,并建立其环境适应能力模型。
(2) 根据各项工作条件的变化情况,对其进行环境区段划分,并根据该区段的实际工作条件确定当前区段的工作条件模型。
(3) 根据环境区段划分和该区段下各项工作条件的变化情况确定第一级变迁的控制时钟。
(4) 根据2.2节建立部件的CTHSPN可靠性模型,并根据部件间的动态关系建立系统的可靠性模型。
(5) 用蒙特卡罗法仿真,计算出系统工作某时长后的可靠度。首先,设置库所初始标识,然后判断各变迁是否使能。瞬时变迁使能后立即实施。时延随机变迁使能后则根据当前实施速率产生一随机时间值,若产生的时间值大于系统已运行时间,则认为系统仍工作;否则该变迁立即实施并输出标识,然后处理下一级变迁。经上述程序后,若在该时刻点系统失效状态库所存在标识,则判定系统失效。经过多次仿真,得到系统工作的次数与仿真总次数的比值即为此时系统的可靠度。仿真总次数越多,得到的可靠度越准确。
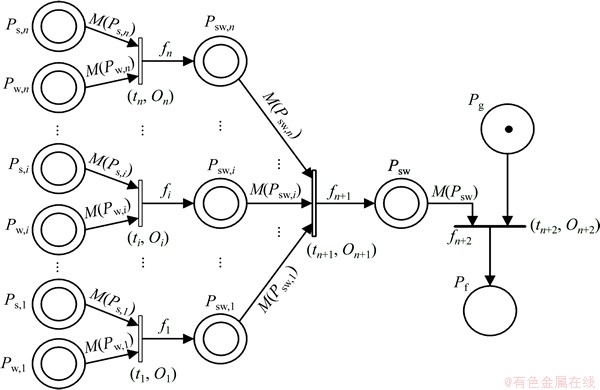
图3 基于CTHSPN的产品可靠性模型
Fig. 3 Product’s reliability model based on CTHSPN
3 实例分析
设有一火车按时刻表往返于A和D 2地,途经B和C 2站,运行情况如表1所示。火车到达A和D站后各休整4 h。车上有1双机冷备电子系统(部件寿命服从指数分布,工作时标称失效率λm为3.1×10-4/h,冷备时失效率为0,火车休整期间系统继续工作),不考虑切换失效,我们采用基于CTHSPN的电子系统可靠性评价方法对其进行可靠性评价。
表1 火车运行情况表
Table 1 Running conditions of train
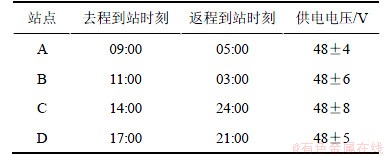
(1) 影响部件可靠性的环境条件为电压和温度。部件的理想工作电压为48 V,电压适应范围为36~60 V;理想工作温度为20 ℃,温度适应范围为-15~55 ℃。根据指标近似法,可得部件的电压和温度适应云分别为SC,1=CV[48, 4,0.4],SC,2=CT[20, 11.7,1.2]。
(2) 部件实际的工作电压大小与变电所的供电情况有关,变电所分别设于A,B,C和D 4地,火车运行于2站之间时,由上一站的变电所为其供电,因此将电压分为4个环境区段。在同一区段内,经过电压转换后,部件的实际电压以48 V为中心,按近似正态分布规律作一定幅度的随机波动,如表1所示。据此,采用云模型来描述部件的实际电压情况,分别为:
WC,1-A=CV[48, 1.33,0.13],WC,1-B=CV[48, 2,0.2],
WC,1-C=CV[48, 2.67,0.27],WC,1-D=CV[48, 1.67,0.17]。
车外的温度变化约为时间的余弦函数,因此,对于车外温度仅划分1个环境区段。设车外温度变化的年均温度为15 ℃,年均温差40 ℃,日均温差12 ℃,则车外某时刻的温度可由下式近似表示:
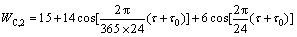 (8)
(8)
其中:WC,2表示车外温度情况;τ0为火车初运行时刻距时间原点的时长(时间原点为一年中车外温度最高的时刻,本例中设8月1日14:00为时间原点,火车于时间原点初运行,即τ0=0);τ为火车已运行时长。
(3) 由电压的区段划分及表1,可得1个周期内(24 h)与电压相关的第一级变迁的控制时钟分别间隔3,7,3,2,6,3 h触发。根据温度变化情况,与温度相关的第一级变迁的控制时钟设为每小时触发1次。
(4) 根据2.2节的部件可靠性模型和步骤(1)~(3)可以得到该系统的CTHSPN可靠性模型,如图4所示。其中t1和t2为第一级变迁,其控制时钟O1和O2由步骤(3)确定;控制时钟O3由O1和O2叠加而成,O5=O4=O3。各变迁1个周期内的控制时钟如图5所示。

图4 双机冷备系统的CTHSPN可靠性模型
Fig. 4 CTHSPN model of dual module hot-standby system
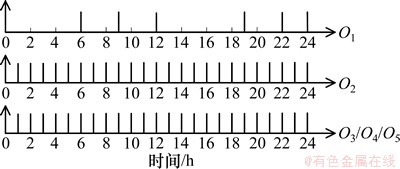
图5 各变迁的控制时钟
Fig. 5 Control clocks of transitions
库所Ps,1和Ps,2分别代表部件的电压、温度适应能力;Pw,1和Pw,2分别代表部件实际工作时的电压、温度情况;Pg,1和Pf,1和Pg,2和Pf,2分别代表主部件和备部件的正常、失效状态。根据步骤(1)~(3),得4个库所的标识函数分别为:
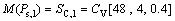 (9)
(9)
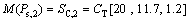 (10)
(10)
 (11)
(11)
式中:n为自然数0,1,2,3…(以下同)。
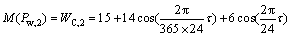 (12)
(12)
控制函数f1和f2的表达式同式(5),f3同式(6),f4和 f5同式(7)。
(5) 采用蒙特卡罗法对系统一年内的可靠度进行仿真分析,并将所得结果与按文献[11]的CHSPN模型法所得结果进行比较,图6和图7所示分别为时间约为1 300 h和2 000 h的仿真结果比较。
由图6和图7可见:采用2种方法得出的系统可靠度曲线都大致以24 h为1周期作上下波动,这种波动主要由车外温度的昼夜变化导致,说明2种方法均能体现温度对系统可靠性的影响。但采用CTHSPN法得到的可靠度曲线在24 h周期性波动内,还存在约3,7,3,2,6和3 h间隔的不同幅度的小波动,这种周期内的波动主要由电压环境的变化造成;而采用CHSPN方法,由于将温度和电压进行归一处理,没能体现电压环境的变化及其单独作用,在可靠度曲线上看不到电压环境的变化造成的周期内波动(图6中CHSPN法可靠度曲线周期内的2次波动是因为此时最高气温高于理想温度20 ℃,24 h内温度需2次经过20 ℃造成,图6中用CTHSPN法得到的曲线同样可以看到这种波动)。同时,采用CTHSPN法得到的曲线中,图6中电压变化造成的周期内波动比较剧烈,而图7的周期内波动较小。这是因为图6所对应的时间约为秋季,温度比较接近20 ℃且温差较小,温度变化对系统可靠度的影响相对较小,造成电压对系统实际可靠度的影响作用较为明显,使得1周期内曲线产生较剧烈波动;图7所对应的时间已进入冬季,温度低且温差较大,温度对系统可靠度的影响起主导作用,电压对可靠度的影响相比很小,造成1周期内可靠度曲线的波动很小。同样,也可以知道在春季,系统的可靠度变化由温度和电压共同作用,而在夏季,系统的可靠度主要受温度影响。而采用CHSPN法得到的曲线,未见各因素的单独的影响作用及影响效果。因此,CTHSPN法比CHSPN法更好地体现温度、电压等条件各自对电子系统可靠性的影响,其得到的可靠性评价结果更符合系统的实际情况。

图6 系统可靠度曲线1
Fig. 6 System reliability curves 1
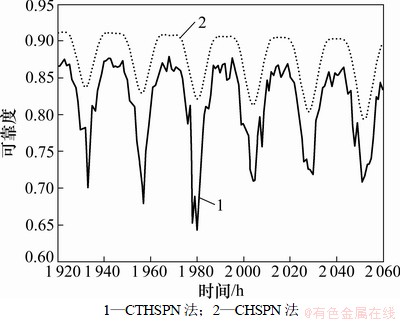
图7 系统可靠度曲线2
Fig. 7 System reliability curves 2
4 结论
(1) 在混合随机Petri网的基础上,通过采取将库所标识扩展到云域并与时间关联、引入控制函数和控制时钟等措施,提出一种CTHSPN模型。
(2) 在CTHSPN模型的基础上,根据Petri网的建模机制及工作条件对电子产品可靠性影响的特点,建立一种基于CTHSPN的电子产品可靠性模型。
(3) 从基于CTHSPN的部件可靠性模型出发,由系统的失效机制和部件间的动态关系建立系统的可靠性模型并采用蒙特卡罗仿真法求解可靠度,从而形成基于CTHSPN的电子系统可靠性评价方法。实例分析表明,基于CTHSPN的电子系统可靠性评价方法具有强大的工作条件动态描述能力,较好地体现各项工作条件对电子系统可靠性的独立性影响作用,为变环境变工作条件下电子系统的可靠性评价提供一条有效的途径。
参考文献:
[1] 曹晋华, 程侃. 可靠性数学引论[M]. 3版. 北京: 高等教育出版社, 2012: 1-6.
CAO Jinhua, CHENG Kan. Introduction to reliable mathematics[M]. 3rd ed. Beijing: Higher Education Press, 2012: 1-6.
[2] 吴晗平. 光电系统环境与可靠性[M]. 北京: 科学出版社, 2009: 66-106.
WU Hanping. The environment and reliability of photoelectric system[M]. Beijing: Science Press, 2009: 66-106.
[3] Leuschen M L, Walker I D, Cavallaro J R. Evaluating the reliability of prototype degradable systems[J]. Reliability Engineering and System Safety, 2001, 72(1): 9-20.
[4] GJB/Z 299C—2006, 电子设备可靠性预计手册[S].
GJB/Z 299C—2006, Reliability prediction handbook of electronic equipments[S].
[5] 李德毅, 孟海军, 史雪梅. 隶属云和隶属云发生器[J]. 计算机研究与发展, 1995, 32(6): 15-20.
LI Deyi, MENG Haijun, SHI Xuemei. Membership clouds and membership cloud generators[J]. Journal of Computer Research and Development, 1995, 32(6): 15-20.
[6] 李德毅, 杜鹢. 不确定性人工智能[M]. 北京: 国防工业出版社, 2005: 137-186.
LI Deyi, DU Yi. Artificial intelligence with uncertainty[M]. Beijing: National Defense Industry Press, 2005: 137-186.
[7] 宋远骏, 李德毅, 杨孝宗, 等. 电子产品可靠性的云模型评价方法[J]. 电子学报, 2000, 28(12): 74-76.
SONG Yuanjun, LI Deyi, YANG Xiaozong, et al. Reliability evaluation of electronic products based on cloud models[J]. Acta Electronica Sinica, 2000, 28(12): 74-76.
[8] 宋远骏, 李德毅, 杨孝宗, 等. 考虑环境因素的计算机可靠性云模型评价[J]. 计算机研究与发展, 2001, 38(5): 631-636.
SONG Yuanjun, LI Deyi, YANG Xiaozong, et al. Reliability count evaluation of computers based on cloud models for environmental factors[J]. Journal of Computer Research and Development, 2001, 38(5): 631-636.
[9] FU Qian, CAI Zhihua, WU Yiqi, et al. A novel reliability evaluation method for series-parallel systems based on cloud model[J]. Journal of Computational Information Systems, 2010, 6(10): 3237-3245.
[10] SHAO Ying, LI Xiaoming. Simulation and analysis of the reliability of the cloud model-based automatic environmental monitoring system[C]//Proceedings of 2011 Asia-Pacific Power and Energy Engineering Conference. Wuhan: IEEE, 2011: 1-5.
[11] 原菊梅, 侯朝桢, 王小艺, 等. 考虑环境因素的分布式系统可靠性建模及其分析[J]. 控制与决策, 2007, 22(3): 309-312.
YUAN Jumei, HOU Chaozhen, WANG Xiaoyi, et al. Distributed system reliability modeling and analysis considering environment factors[J]. Control and Decision, 2007, 22(3): 309-312.
[12] 原菊梅. 复杂系统可靠性Petri网建模及其智能分析方法[M]. 北京: 国防工业出版社, 2011: 1-160.
YUAN Jumei. Reliability modeling and intelligence analysis methods of complex systems based on Petri nets[M]. Beijing: National Defense Industry Press, 2011: 1-160.
[13] Ramos G, Sanchez J L, Torres A, et al. Power systems security evaluation using Petri net[J]. IEEE Transactions on Power Delivery, 2010, 25(1): 316-322.
[14] 邵立周, 刘艳玲, 吴晓平. 船舶电力系统可靠性评估的自适应模糊Petri网方法[J]. 海军工程大学学报, 2010, 22(2): 6-10.
SHAO Lizhou, LIU Yanling, WU Xiaoping. Adaptive fuzzy Petri-net method for reliability evaluation of shipboard power system[J]. Journal of Naval University of Engineering, 2010, 22(2): 6-10.
[15] Katsigiannis Y A, Georgilakis P S, Tsinarakis G J. A novel colored fluid stochastic Petri net simulation model for reliability evaluation of wind/PV/diesel small isolated power systems[J]. IEEE Transactions on Systems, Man and Cybernetics, 2010, 40(6): 1296-1309.
(编辑 邓履翔)
收稿日期:2012-07-03;修回日期:2012-09-14
基金项目:国家自然科学基金资助项目(61134001);中央高校基本科研业务费专项资金资助项目(2009YJS014)
通信作者:覃庆努(1980-),男,广西柳江人,博士研究生,从事可靠性理论和系统可靠性研究;电话:010-51688165;E-mail:08111020@bjtu.edu.cn