基于混合优化算法的地震数据匹配追踪分解

蔡涵鹏^{1, 2}，贺振华^{2, 3, 4}，高刚³，黄德济³

(1. 中国石油川庆钻探工程有限公司 地球物理勘探公司，四川 成都，610213；

2. 成都理工大学 油气藏地质及开发工程国家重点实验室，四川 成都，610059；

3. 成都理工大学 地球物理学院，四川 成都，610059；

4. 成都理工大学 地球探测与信息技术教育部重点实验室，四川 成都，610059)

摘要：以5个参数(幅度、频率、相位移、尺度因子、时移)控制的Morlet小波作为匹配子波原子，在确定控制参数的过程中，提出应用具有全局优化能力的粒子群优化算法与具有局部优化能力的BFGS算法的混合优化算法，能够使得匹配追踪算法不再依赖于复数道分析确定子波原子的振幅、频率和相位的初值。控制子波时间延续长度的尺度因子是一个重要的参数。匹配追踪分解后，消除较小和较大的尺度因子和分解终止时的剩余信号能够有效地压制地震数据噪声。利用局部函数解析表达式和残差信号能量进行有效地控制算法的迭代次数可以提高计算效率。数值试验和实际资料的应用均表明:利用本文方法能够压制地震数据噪声，对地震信号快速地、精确地进行时频谱分析，为烃类检测和储层描述提供有效的手段。

关键词：Morlet小波；匹配追踪；粒子群算法；BFGS算法；时频分析；混合优化算法

中图分类号：P631.4          文献标志码：A         文章编号：1672-7207(2013)02-0687-08

Seismic data matching pursuit using hybrid optimization algorithm and its application

CAI Hanpeng^{1, 2}, HE Zhenhua^{2, 3, 4}, GAO Gang³, HUANG Deji³

(1. Geophysical Exploration Company, Chuanqing Drilling Engineering Co. Ltd., CNPC, Chengdu 610213, China;

2. State Key Lab of Oil and Gas Reservoir Geology and Exploration,Chengdu University of Technology, Chengdu 610059, China;

3. College of Geophysics, Chengdu University of Technology, Chengdu, Sichuan, 610059, China;

4. Key Lab of Earth Exploration and Information Techniques of Ministry of Education,Chengdu University of Technology, Chengdu 610059, China)

Abstract: Morlet wavelet with five parameters, including amplitude, frequency, phase, scale factor and time delay, as atoms in the matching pursuit decomposition was employed. In the processing of established controlled variable, hybrid optimization algorithm was introduced, including particle swarm optimization and BFGS method, so as to in-depend on complex-trace analysis to determine initial value of controlled variable, such as amplitude, frequency, and phase. The scale factor is an important adaptive parameter that controls the width of wavelet in time. After matching pursuit decomposition, removing wavelets with either very small or very large scale value and residual signal can suppress spikes and sinusoid functions, and rand noise effectively from seismic data. For fast matching pursuit algorithm, analytical expressions and the energy of the residual signal were employed which control effectively the iterating times. Synthetic data test and results of practical data application show that using method in the paper has good effect in the aspect of attenuating noise form seismic data, fleetly and accurately implementing time-frequency analysis, and provide an effective means for hydrocarbon detection and reservoir description.

Key words: Morlet wavelet; matching pursuit decomposition; particle swarm optimization; BFGS method; time-frequency analysis; hybrid optimization algorithm

匹配追踪算法是Mallat等^[1]提出作为信号稀疏分解中应用较为普遍的一种算法。匹配追踪算法克服了时窗傅里叶变化不能描述信号结构变化和小波变换不能提供精确估算子波原子频率的缺点^[2]。匹配追踪算法具有较高的时频分辨率、暂态结构的局部自适应性、信号结构的参数表示等优良特性，能够较好地适应信号分析^[3-6]。最近，国内外一些学者将匹配追踪算法应用于地震信号分析^[7-10]。匹配追踪算法从一个过完备的子波原子库出发，采用某种策略每次选取与地震道信号最匹配的基(也称为原子域或时频原子)，最终将地震道信号表示为若干时频原子的线性组合。应用匹配追踪算法，创建超完备子波库所使用的子波原子基与原始信号越相似，则分解效果越好，因此，需要选择合适的原子基。本文作者以Morlet小波作为基本匹配子波，其原因在于Morlet小波适合具有能量吸收和速度频散的地震信号的时频分析^[11-12]。由于地震信号具有非平稳特征，为了能够对地震道信号更好地进行时频谱分析，需要选择具有幅度、时间延迟、尺度、频率和相位移参数的小波原子。常规的匹配追算法是一种不断迭代、寻求最佳匹配的贪婪算法，子波库中的可供选择用于匹配的子波是固定的，1次迭代只能确定1个匹配子波，对子波库的全方位扫描会需要大量的计算机运行时间，导致搜索效率很低，不适合于大规模三维地震资料处理。为了提高计算效率，Liu等^[9-10]将地震信号的瞬时特征引入到匹配追踪算法中，Wang^[13]提出三步法实现匹配追踪，张繁昌等^[14]提出了双参数快速匹配追踪算法，张显文等^[15]提出两步法匹配追踪算法，提高了匹配追踪算法的效率，并用于河道砂体识别、随机噪声消除、含气储层烃类检测和时频分析等。每次迭代寻找最优匹配小波的过程本质上是一个寻找非凸的，高度非线性问题的全局最优解的过程。本文作者以5个参数控制的Morlet小波作为基本匹配子波，提出全局优化算法与局部优化算法相结合的混合优化算法，实现一次性计算描述Morlet小波的5个参数，使得计算效率和精确度得到提高。匹配追踪算法具有较强的多解性。为了减少多解性和使得分析信号更快地被分解，利用残差信号能量与分解子波能量之比最小作为目标函数。对基于混合优化算法快速匹配追踪算法的迭代次数进行有效控制，不仅有效地避免了毫无意义的计算，在一定程度上也能减少解的多解性。由于匹配追踪算法具有自适应的分解特点，具有较高的时频分辨率，考虑到各个子波原子之间的独立性，通过计算每次分解得到子波原子的Wigner-Ville 分布，将所有原子的时频分布叠加到一起构成整个地震道信号的高分辨时频分布，以满足高精度时频分析、流体检测和时频属性提取的要求，为烃类检测和储层描述等提供有效的手段。

1  方法原理

1.1  匹配追踪基本思想

构建信号的时频原子基函数集，它由窗函数经平移、伸缩、相位移和频率调制而成，其形式如下：

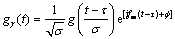        (1)

式中：σ为尺度因子；τ为时间平移因子；f_m为频率调制因子；f为相位移因子；记γ=γ(σ，τ，f_m，f)，γ∈Γ；Γ=R⁺×R×R；g(t)为窗函数。

利用式(1)构建1个时频原子基函数集合M{g_γ(t)}_γ∈Γ，匹配追踪算法通过迭代的方式，每次从时频原子集合中选择一个时频原子g_γi(t)∈M，将需要分解的信号s(t)投影到某个时频原子g_γi(t)上，并计算信号的剩余部分R_s，使得

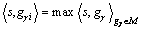          (2)

式中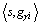：表示内积运算；max表示最大化，使提取的能量最大程度地匹配信号的剩余能量。经过N次搜索迭代过程，不断地对剩余信号R_s进行这一操作，使得分解后的剩余信号能够较快的衰减，直到小于预先设定的终止条件，迭代结束，从而将原始信号s(t)自适应地分解成一组时频原子的线性表示，其形式为

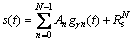          (3)

式中：A_n是第n次提取的时频原子基g_γn(t)的幅度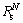；是原始信号经过N次迭代分解后的残余信号。

匹配追踪算法成功的关键之一是选取适合于信号分析的时频原子。对于地震信号，选择Morlet小波作为时频原子，其原因在于Morlet小波与地震子波具有良好的相似性，可以通过Morlet小波的伸缩、频移、相位移和频率调制来匹配实际地震数据，得到较好的分解结果。由5个参数表征的Morlet小波的时间表达式为：

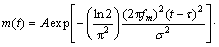
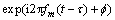            (4)

式中：A为小波的幅度。

匹配追踪算法成功的关键之二是精确地获取用于描述时频原子的参数。

1.2  参数优化算法

匹配追踪算法是一种不断迭代寻找最佳匹配的贪婪算法^[1]，从巨大的时频原子集合形成的解空间中反复迭代搜索最佳匹配的计算效率低，是一个NP完全问题^[16-17]，为了保证在实际地震数据处理中的实用性和应用性，需要提高最优时频原子的搜索运算效率。Liu等^{[9-10, 13-14]}描述时频原子的参数获取方法均是基于复数道分析的思想，应用复数道分析获得时频原子的时间位移、相位移、频率等参数。然而，本文作者在研究中发现，针对于一个单波而言，复数道分析获得瞬时振幅包络最大值以及对应位置的瞬时相位和瞬时频率能够准确地确定时频原子的时间位移、相位移和频率，而对于像地震信号的调谐复波，复数道分析获得参数并不能精确地用于描述时频原子的参数，尤其是频率属性(瞬时频率可能为负值)。匹配追踪算法的整个分解过程实质上是一个多参数寻优过程，而粒子群优化算法是一种简单、有效的随机全局优化算法，可以解决大量非线性和多极值的复杂问题，具有概念简单，易于实现，搜索速度快的优点，但是，由于粒子群优化算法中所有粒子都向最优解的方向飞去，粒子趋向同一化，群体多样性逐渐消失，致使后期算法的收敛速度明显变慢，甚至处于停滞状态为了克服这一缺点，引进在局部算法中有着完善的数学理论基础，采用不精确线性搜索时的超线性收敛性和处理实际问题能力的BFGS算法。本文将粒子群优化算法与BFGS算法相结合的混合优化算法引进到匹配追踪算法中，解决匹配追踪过程中的参数寻优问题，提高搜索最优解的精确度和效率。

1.2.1  粒子群优化算法

粒子群优化算法是一种基于迭代寻优的优化算 法^[18-19]。鸟被作为没有质量和体积的微粒，并延伸到N维空间。粒子在N维空间的位置表示为X_i=(x₁，x₂，…，x_N)的向量，飞行的速度表示为V_i=(v₁，v₂，…，v_N)的向量。每一个粒子都有一个目标函数的适应度，并且已知粒子本身到目前为止发现的最好位置P_best (粒子自己的飞行经验)、现在的位置X_i和到目前为止整个群体中所有粒子发现的最佳位置P_best,g (粒子同伴的飞行经验)。粒子就是通过自己的经验和同伴中最好的经验来确定下一次飞行。粒子群优化算法首先将粒子初始化为一群随机粒子，然后，通过下列公式更新自己的速度位置，迭代寻找最优解：

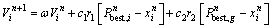 (5)

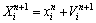                (6)

式中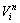：为粒子i在第n次迭代的速度；ω为惯性因子；c₁和c₂为学习因子，为正常数，分别代表粒子的局部和全局学习能力；r₁和r₂为[0，1]的随机数。另外，为了粒子在解空间内飞行，在迭代过程中，设置飞行速度和粒子位置的边界。但是，由于在搜索过程中，粒子的搜索方位局限在P_best和P_best,g附近，因此不能保证以概率1收敛到全局最优解。

1.2.2  BFGS方法

BFGS方法是一个拟牛顿方法，具有二次终止性、整体收敛性和超线性收敛性，算法产生共轭的搜索方法^[20]。算法的收敛性速度比仅为线性收敛的梯度最速下降法的速度快。在实际计算过程中，由于舍入误差的存在及一维搜索的不精确性，导致BFGS算法效率的影响也比梯度最速下降法和共轭梯度法小，且精度均较后两者的高。BFGS方法是一个有效的局部优化算法。BFGS算法求解无约束优化问题min(f(x))的主要步骤如下：

第1步：确定变量维数N和BFGS算法收敛精度ε，给初始解赋值x₀∈Rⁿ，k=0；

第2步：计算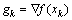，若g₁≤ε，则令x^*=x₀，f^*=f(x₀)，算法停止，否则，计算d_k=-H_kg_k；

第3步：沿着方向d_k做线性搜索求取α_k＞0，且令x_k+1=x_k+α_kd_k；

第4步：校正H_k产生H_k+1使得拟牛顿条件成立。其中：

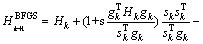
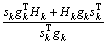
第5步：令k=k+1，转入第2步。

在上述的算法中，初始Hesse逆近似H₀通常取单位矩阵。

1.2.3  混合算法描述

为了克服具有良好全局优化的粒子群优化算法在优化后期阶段收敛速度慢，甚至停滞状态的问题，在粒子群优化算法后期中引入BFGS方法，利用BFGS方法的整体收敛性和超线性收敛性来加速收敛速度。BFGS方法属于局部优化算法，其优化结果的好坏取决于初始位置的选择，因此，利用具有全局搜索能力的粒子群算法提供给BFGS方法初始解位置。将两种优化算法结合的混合算法就能取长补短，改善优化的结果和速度。简单的混合使用2种优化算法，并不能取得理想的效果，原因在于粒子群优化算法可能过早陷入局部最优，使得粒子群优化算法变异能力差。由于BFGS方法中采用不精确一维搜索，在搜索过程中，设定最大搜索次数，若超过最大搜索次数，则表明BFGS方法已经陷入局部最优，同时也表明上次粒子群优化算法结果并不是BFGS算法的一个良好初值，此时，应该提前结束BFGS搜索，在BFGS算法所得的最后一次解的较大范围内生成新的种群空间。此外，若BFGS算法搜索过程中g_k+1≤ε，则比较目标函数与预设值之间的大小，若目标函数值大于预设值，则在当前解x^*较小的空间范围内生成新的种群空间x_k，然后，从新的种群空间中开始进行粒子群搜索，重复此过程直到目标函数小于预设值为止。生成新种群空间的公式为

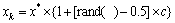         (7)

式中：c为调节常数；rand( )∈(0，1)的随机数。

1.3  目标函数及迭代终止准则

上述的优化算法均是求取目标函数极小值。优化的参数包括描述时频原子的幅度、频率、相位移、尺度因子和时间位移5个变量。为了表达方便，将式(2)的目标函数改写为

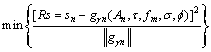      (8)

即使得每次分解后剩余信号能量与分解子波能量比值最小。

由于实际的地震记录中包含随机噪声，在迭代初期，残差能量急剧减少，但是在一定水平时，残差能量基本保持一个相对稳定的水平。其原因在于当分解至噪声水平时，随机噪声使得从残差信号中减去匹配子波时出现“此消彼长”的显现，使得剩余信号能量变化非常小，将此时剩余信号能量作为收敛能量阀值。一旦信号分解后剩余能量达到收敛能量阀值，继续迭代将耗费机时，且毫无意义。因此，在实际地震信号匹配追踪分解时，可以随机抽取若干地震道进行试验分析，确定收敛能量阀值以及分解次数，可以提高匹配追踪的效率。在实际的程序中也可以设置分解后剩余能量相对于分解前信号能量的百分比进行终止分解条件，从而达到能够自适应地终止匹配追踪分解。

1.4  构建时频谱

信号s(t)分解成为一组时频原子的线性组合后，再求出每个时频原子的Wigner-Ville分布，既可以保持Wigner-Ville分布具有高的时频分辨率特点，又可以避免直接求原信号Wigner-Ville分布的交叉项干扰，能够得到高质量的时频能量分布。针对Morlet小波作为时频原子基，时频振幅谱的解析表达式为：

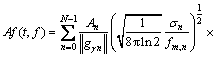
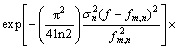
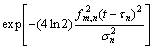         (9)

式中：f_m,n为第n个匹配子波的平均频率；||g_γn||为标准化因子，其解析表达式为

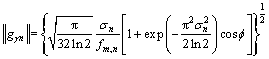 (10)

利用式(10)能够提高式(8)和(9)的计算速度。

2  数值试验分析

图1所示为由不同主频、相位、时间位移、尺度因子及幅度的4个子波合成的地震记录。利用本文提出的方法将合成地震记录进行分解，并利用式(3)进行重构。经过自适应快速时频分解后，得到的时频谱分布如图2(a)所示，由于在时频原子基的搜索过程中采用了具有全局寻优的微粒群优化算法及局部寻优的BFGS算法，使得搜索速度加快，运算效率得到一定程度提高。比较图2(a)与基于短时傅里叶变换(图2(b))的时频谱可见：基于匹配追踪分解的各个信号分量在时频平面的位置精确，具有良好的时频聚集性，它们的时频分辨率几乎达到极限。图2(b)所示的时频聚集性能明显比前者的差。短时傅里叶变换聚集性能差的原因在于强烈依附于窗函数的选择。图3所示为合成地震记录与匹配追踪重构地震记录的对比，由图3可见：地震道可以完全由匹配子波重构，其重构地震记录与原始合成地震记录的残差与原始信号在同一数量级上比较，其强度和能量很弱，说明分解是可靠的。其合成地震记录的分解次数和能量衰减关系如图4所示。由图4可见：本文提出的基于混合优化算法的匹配追踪方法能够精确地获得每次分解子波原子的控制参数，且能量的衰减趋势表明分解过程是收敛的。

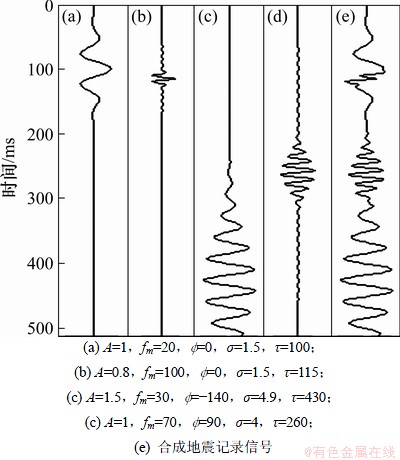
图1  不同主频、相位、尺度、时移、幅度的Morlet子波合成的地震记录

Fig.1  Synthesis signal records using Morlet wavelets with different dominant frequencies, phases, scale factors, time delays, and magnitudes

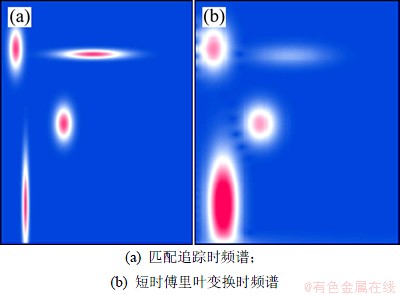
图2  合成信号的时频谱

Fig.2  Time-frequency spectral for synthesis signal

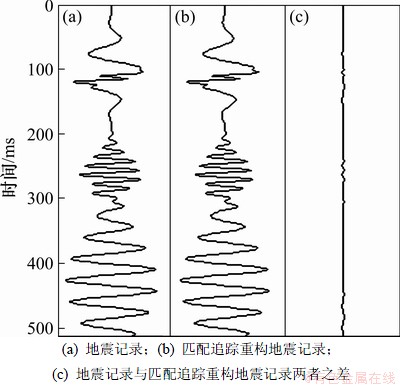
图3  合成地震记录的匹配追踪结果

Fig.3  Results of matching pursuits for synthetic seismic records

为了验证算法的稳定性，在合成地震记录中(图1)加入最大幅度为0.2的高斯随机噪声。利用本文提出的匹配追踪算法将其进行分解，并用各个匹配子波进行信号重构。图5所示为加入随机噪声后的匹配追踪结果。由图5可见：匹配追踪结果较好地将有效信号进行重构，并能够有效消除随机噪声。值得注意的是，对含有噪声的信号，首先分析信号的信噪比，也能够有效地确定匹配追踪分解的终止准则。

在控制morlet时频原子的5个参数中，尺度因子σ有着重要的意义。尺度因子σ控制着子波的延续长度。σ越大，子波延伸长度越长，反之，子波长度延伸越短。在地震波的有效信号中，子波的长度是有一定限度的，因此，在应用匹配追踪算法重构地震信号时，可以通过控制尺度因子对含噪地震信号进行噪声压制。图6所示为含噪合成地震信号应用匹配追踪分解后，消除尺度因子σ大于4的子波以及噪声的效果图。从匹配追踪结果中消除σ较小的子波，能够有效地压制具有尖峰特征的噪声。通过从匹配追踪结果中消除σ特别大的子波，能够有效压制像正弦或者余弦特征的噪声，例如，地震测线上空高压输电线电流引起的地震记录中从浅到深层的1个50 Hz左右的单频干扰。

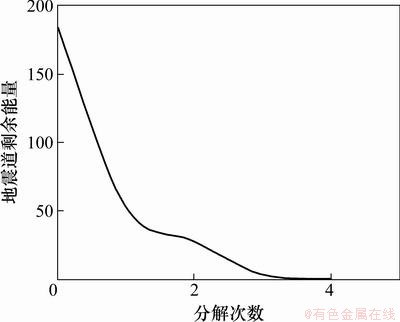
图4  分解次数与能量衰减的关系

Fig.4  Relationship between decomposition times and energy attenuation

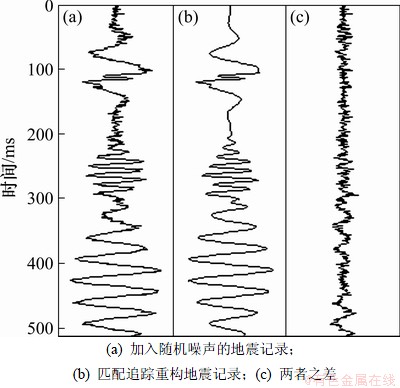
图5  合成地震记录加随机噪声后的匹配追踪结果

Fig.5  Results of matching pursuits for synthetic seismic records added random noise

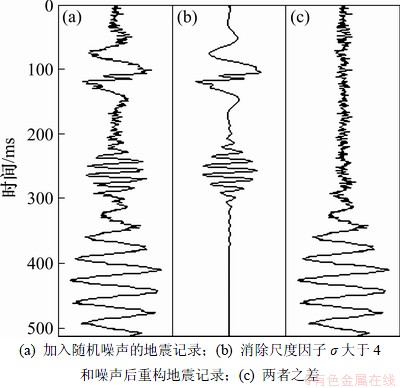
图6  尺度因子滤波结果

Fig.6  Filtering results of scale factor

3  实例分析

基于混合优化算法完成的匹配追踪方法应用于实际地震数据的噪声压制和时频谱分析。图7(a)所示为原始地震振幅剖面(图中从上到下，第1个层位为E3d2U，第2个层位为E3d2M，第3个层位为E3d2L，竖线为钻井位置，钻井资料显示气藏位于白色箭头标注，即E3d2M层之上)。原始地震数据中包含较大的随机噪声，导致资料的信噪比较低。从原始地震数据中减去匹配追踪获得的尺度因子σ＜0.3和σ＞8的子波分量以及匹配追踪过程终止时剩余信号，得到重构的地震振幅剖面(图7(b))。经过匹配追踪滤波重构的地震振幅剖面中信噪比明显得到提高，同相轴的连续性得到加强，断点更加清晰。由于基于控制参数σ和剩余能量信息的滤波与常规的截频滤波(如F-K滤波)有显著的差异，本文方法能够有效地保留地震数据的有效频率信息。

由于大地滤波作用和地层中流体的黏滞性导致地震波的高频吸收快，地震子波逐渐变长。Morlet小波适当地描述了孔隙介质中波传播时能量吸收和相位失真特征，因此，Morlet小波适合于含气储层的声学特性分析。Castagna等^[8]指出，在含气储集层的下方存在低频阴影的效应，表现为在低频切片上具有较高的能量异常。图8所示为一组基于本文方法获得的不同频率的共频率剖面。从图8可见：在12 Hz(图8(a))时，油气层(白色箭头标注)显示为强能量，其下部瞬时谱能量也强(黑色圈注)，即存在低频“上强下强”的低频伴影特征。随着频率增至20 Hz和28 Hz(图8(b)和(c))，油气层为强能量显示，但下部伴影能量明显减弱，而当频率增至36 Hz时(图8(d))，油气层仍显示为强能量，但下部的伴影能量消失。

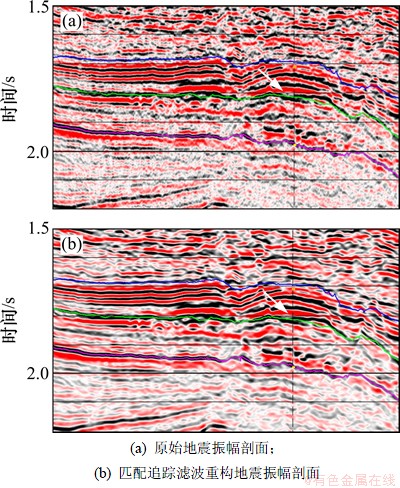
图7  地震振幅剖面

Fig.7  Seismic profile

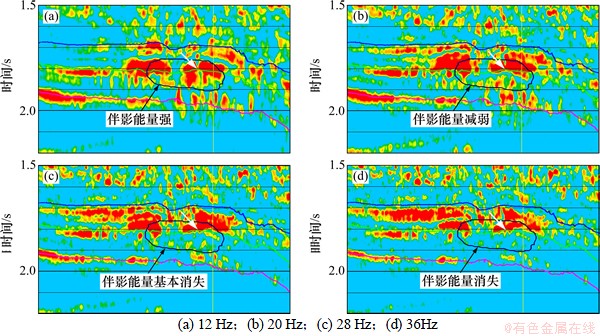
图8  基于匹配追踪的共频率剖面

Fig.8  Isofrequency profile using matching pursuits

4  结论

(1) 所提出的基于具有全局优化能力的粒子群优化算法和具有局部优化能力的BFGS算法的自适应匹配追踪算法，使得匹配追踪算法不再依赖于复数道分析确定时频原子的振幅、频率和相位的初值，能够在整个解空间中搜索最优的时频原子控制参数，提高了匹配追踪的精确度，并且使得匹配追踪算法的计算效率提高。应用局部函数的解析表达式和根据信噪比确定匹配追踪的停止准则，能够进一步提高计算效率。

(2) 通过选择不同的子波尺度因子和剩余能量占原始信号能量的百分比，能够有效地压制噪声，并且该算法结合Wigner-Ville分布可以对地震信号进行快速时频谱分析，刻画不同频率的响应特征，为烃类检测和储层描述提供有效的手段。

参考文献：

[1] Mallat S, Zhang Z. Matching pursuit with time- frequency dictionaries[J]. IEEE Trans Signal Process, 1993, 41(12): 3397-3421.

[2] Qian S, Chen D. Signal representation via adaptive normalized Gaussian functions[J]. Signal Processing, 1994, 36(1): 1-11.

[3] Rebollo-Neira L, Lowe D. Optimized orthogonal matching pursuit approach[J]. IEEE Signal Process Letters, 2002, 9(4): 137-140.

[4] Capobianco E. Independent multi-resolution component analysis and matching pursuit[J]. Computational Statistics & Data Analysis, 2003, 42(6): 385-402.

[5] Andrle M, Rebollo-Neira L, Sagianos E. Backward-optimized orthogonal matching pursuit approach[J]. IEEE Signal Process Letters, 2004, 11(9): 705-708.

[6] Andrle M, Rebollo-Neira L. A swapping-based refinement of orthogonal matching pursuit strategies[J]. Signal Processing, 2006, 86(3): 480-495.

[7] Wang B, Pann K. Kirchhoff migration of seismic data compressed by matching pursuit decomposition[C]//66th Annual International Meeting. Denver, Colorado: SEG, Expanded Abstracts, 1996: 1642-1645.

[8] Castagna J P, Sun S J, Siegfried R W. Instantaneous spectral analysis: Detection of low-frequency shadows associated with hydrocarbons[J]. The Leading Edge, 2003, 22(2): 120-127.

[9] Liu J, Marfurt K J. Matching pursuit decomposition using Morlet wavelet:[C]//75th Annual International Meeting. Houston, Texas: SEG, Expanded Abstracts, 2005: 786-789.

[10] Liu J, Wu Y, Han D, et al. Time-frequency decomposition based on Ricker wavelet[C]//74th Annual International Meeting. Denver, Colorado: SEG, Expanded Abstracts, 2004: 1937-1940.

[11] Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory: Part I. Complex signal and scattering in multilayered media[J]. Geophysics, 1982, 47(2): 203-221.

[12] Morlet J, Arens G, Fourgeau E, et al. Wave propagation and sampling theory: Part II. Sampling theory and complex waves[J]. Geophysics, 1982, 47(2): 222-236.

[13] Wang Y H. Seismic time-frequency spectral decomposition by matching pursuit[J]. Geophysics, 2007, 72(1): v13-v20.

[14] 张繁昌, 李传辉, 印兴耀. 基于动态匹配子波库的地震数据快速匹配追踪[J]. 石油地球物理勘探, 2010, 45(5): 667-673.

ZHANG Fanchang, LI Chuanhui, YIN Xingyao. Seismic data fast matching pursuit based on dynamic matching wavelet library[J]. Oil Geophysical Prospecting, 2010, 45(5): 667-673.

[15] 张显文, 韩立国, 王宇, 等. 地震信号谱分解匹配追踪快速算法及应用[J]. 石油物探, 2010, 49(1): 1-6.

ZHANG Xianwen, HAN Li-guo, WANG Yu, et al. Seismic spectral decomposition fast matching pursuit algorithm and its application[J]. Geophysical Prospecting for Petroleum, 2010, 49(1): 1-6.

[16] Gribonval R. Fast matching pursuit with a multi-scale dictionary of Gaussian Chirps[J]. IEEE Trans Signal Processing, 2001, 49(5): 994-1001.

[17] Davis G, Mallat S, Avellaneda M. Adaptive greedy approximations[J]. Constr Approx, 1997, 13(1): 57-98.

[18] Kennedy J, Eberhart R. Particle Swarm optimization[C]// Proceedings of IEEE International Conference on Neural Network. Perth, Western Australia, 1995: 1942-1948.

[19] Sun J, Xu W B. Particle swarm optimization with particles having quantum behavior[C]//IEEE Proceedings of Congress on Evolutionary Computation. Piscataway, New Jersey, 2004: 325-331.

[20] 袁亚湘, 孙文瑜. 最优化理论与方法[M]. 北京: 科学出版社, 2003: 219-234.

YUAN Yaxiang, SUN Wenyu. Optimization theory and methods[M]. Beijing: Science Press, 2003: 219-234.

(编辑  杨幼平)

收稿日期：2012-02-16；修回日期：2012-04-20

基金项目：国家自然科学基金资助项目(41174114，41004054)；国家自然科学基金重点资助项目(40839905)

通信作者：蔡涵鹏(1983-)，男，四川南江人，中国石油川庆钻探工程有限公司西南油气田博士后，从事石油地球物理勘探研究；电话：13880725308；E-mail：caihanpeng@126.com；247133939@qq.com