Trans. Nonferrous Met. Soc. China 24(2014) 1-11

Role of Kirkendall effect in diffusion processes in solids

C. A. C. SEQUEIRA, L. AMARAL

Materials Electrochemistry Group, ICEMS, Instituto Superior , Universidade de Lisbon, Avenida Rovisco Pais 1, 1049-001 Lisboa, Portugal

Received 7 April 2013; accepted 14 July 2013

Abstract: In the 1940s, KIRKENDALL showed that diffusion in binary solid solutions cannot be described by only one diffusion coefficient. Rather, one has to consider the diffusivity of both species. His findings changed the treatment of diffusion data and the theory of diffusion itself. A diffusion-based framework was successfully employed to explain the behaviour of the Kirkendall plane. Nonetheless, the complexity of a multiphase diffusion zone and the morphological evolution during interdiffusion requires a physico-chemical approach. The interactions in binary and more complex systems are key issues from both the fundamental and technological points of view. This paper reviews the Kirkendall effect from the circumstances of its discovery to recent developments in its understanding, with broad applicability in materials science and engineering.

Key words: Kirkendall effect; Kirkendall velocity; Kirkendall planes; diffusion couple technique; solid-state diffusion; interdiffusion

1 Introduction

Diffusion processes play a key role in metallurgy, namely in physical processes such as homogenisation, non-martensitic transformation, precipitation, oxidation or sintering. The first systematic study of diffusion was reported in 1896 by ROBERTS-AUSTEN, who investigated the diffusion of gold in solid lead [1]. In almost all the structural applications containing heterogeneous materials systems, diffusion is ubiquitous at elevated temperature, and, depending on the material systems, even at ambient temperature [2]. The understanding of diffusion processes is also fundamental in a wide range of research fields, from bulk applications as in composite materials or coatings to thin films in microelectronics.

There are two main approaches to study diffusion in solid state: the atomistic approach, where the nature of the diffusion species in atomic level is explicitly considered, and the continuum approach, where the diffusing substance is treated as continuous medium, ignoring the nature of diffusion in atomic level. The later approach has the advantage of allowing the analysis and prediction of micro- and/or macroscopic physico- chemical changes in applications without going to rather complicated atomistic models, where many questions are still to be addressed.

In the early stage of the understanding of solid state diffusion, that is about one century ago, it was believed that atomic diffusion occurred by a direct exchange or a ring mechanism in metallic crystals, as shown in Figs. 1(a) and (b). In 1929, PFEIL [3] studied the oxidation of iron and steel and noticed one peculiar phenomenon: “It had frequently been noted that small particles of foreign matter (such as pieces of muffle) falling on the surface of oxidising iron were gradually buried. The scale grew up round these particles until they finally disappeared beneath the surface, but they could afterwards be found by breaking up the layer of scale”.

These foreign particles were inert to the diffusing species, iron and oxygen, and this observation indicated that iron diffuses through the oxide scale to the surface, where it reacts with oxygen to form oxide.

In 1942, HUNTINGTON and SEITZ [4] showed that diffusion occurs by vacancy mechanism (Fig. 1(c)), not by direct exchange, but at that time this work was overlooked. Four years later, HARTLEY [5] intentionally used titanium dioxide as foreign inert particles for the first time, in an organic acetone/cellulose-acetate system, to study the inequality of the diffusing species. The same technique was then used by SMIGELSKAS and KIRKENDALL in 1947 [6] by introducing molybdenum inert markers at the original interface between the different phases to examine the inequality of diffusivities of the species in the Cu-Zn system. HARTLEY’s work did not get much visibility at that time and the effect of inequality of diffusivities on the movement of the inert marker was named as the Kirkendall effect [8]. Contrary to the common belief at that time, this phenomenon indicated that atomic diffusion occurs through a vacancy mediated mechanism. Since its discovery, the Kirkendall effect has been found in various alloy systems, and research on lattice defects and diffusion developed significantly. The understanding of the Kirkendall effect is important in controlling the bonding between different materials and, in particular, is fundamental in controlling and suppressing the voids that are produced in the boundary region at a bonding interface. Currently, the Kirkendall effect still receives a great deal of attention in various fields in materials science and technology, ranging from structural materials welding, metals and ceramic powders sintering, thin films, high temperature oxidation, to large-scale integration [9-14].

Fig. 1 Atomic diffusion mechanisms

Only three papers were produced by KIRKENDALL in his extremely short research career. However, his research had great scientific and technological impact, which may still be noticed today, more than six decades after the end of KIRKENDALL’s academic career. This paper revisits the KIRKENDALL discovery and his short but significant research activity, and reviews some developments in the understanding of his major role in the diffusion theory.

2 KIRKENDALL’s career

Ernest KIRKENDALL was born in Michigan in 1914. He graduated from Wayne University in 1934, Wayne College at the time, and moved to the Metallurgy Department of the University of Michigan where he was awarded a master’s degree in 1935 and a doctor of science in 1938 under the supervision of UPTHEGROVE. He studied the reviews by DESCH (1912) [15], MEHL (1936) [16], and KRYNITSKY (1937) [17] and was particularly influenced by MEHL’s review. He became very interested in atomic diffusion phenomena in solid metals and in equilibrium-phase diagrams, particularly the phase separation of α-brass and b-brass resulting from the cooling of b-brass alloy. The choice of diffusion in brass for his research topic reflected a combination of those two interests. The previous works on the topic were basically qualitative discussions and a quantitative assessment was needed. Therefore, KIRKENDALL wanted to measure quantitatively the diffusion coefficient of copper and zinc in α-brass, with high accuracy. In his D.Sc. dissertation and first paper [18], he reported zinc diffusivities in brass at three different temperatures.

Figure 2 shows schematically the samples used in the first paper. The side face of the b-brass plate-shaped specimen (with 100 mm length and about 3 mm thickness) was first mirror-polished; it was then electroplated with 250 mm thickness of copper. The specimens were annealed in vacuum at 723 K for about 10 ks to make hydrogen desorb from the specimens. After diffusion anneals in an electric muffle furnace followed by water quenching, a part of the specimen was cut off. The remainder was then used for successive diffusion anneals. An optical microscope was used for the metallographic observation of the polished surface A, whereas the polished surface B was submitted to X-ray diffraction after consecutive sectioning steps of 27-75 mm thickness to measure the lattice parameters. The values were then converted to determine the zinc concentrations in α-brass.

Fig. 2 Schematic of specimen used for study of the first paper [18]

After diffusion anneals, an α-brass phase layer grows on both sides of the bonding interface of copper and b-brass (Fig. 3). The α/b phase boundary is clear since the α-brass layer inside the interface consists of large columnar grains. Conversely, the boundary between the copper-rich α-brass phase outside the interface and the copper phase is not distinct because they have the same crystal structure.

KIRKENDALL was fortunate to originally choose the system of copper and brass. He was able to measure the concentration profiles of copper diffusion in α-brass phase surrounded by both the original and the α/b interfaces. The quantitative analysis was successful due to two reasons. First, the α-brass phase between the original bonding interface and the final α/b interface always grows uniformly in thickness. Second, the fact that the α/b interface could be clearly followed with the optical microscope. It is interesting to note that if the α/b interface and the columnar grains formed on the inside of the original copper b-brass interface had not been distinct, Kirkendall would not have made his important discovery.

At that time, it was accepted that atomic diffusion took place via a direct exchange or ring mechanism, and no other mechanisms had been proposed. Therefore, following his advisor’s suggestion, KIRKENDALL explained the movement of the original interface as a consequence of volume change between α-brass (which has FCC close-packed structure) and b-brass (which has BCC close-packed structure). Additionally, with the assumption of the equality of the diffusivities of copper and zinc, he concluded that the diffusion of these elements must have occurred by the ring mechanism in which four or more atoms participate. He had noticed some discrepancies, but if he had insisted on the inequality of the diffusivities of copper and zinc to explain the original boundary migration, UPTHEGROVE would have opposed his D.Sc. thesis defense [7].

Even though it was not mentioned, KIRKENDALL’s thesis and first paper did not reflect completely his own thought. After finishing his D.Sc. program, KIRKENDALL returned to Wayne University as an instructor. There, after confirmation of the validity of his experiments by repeating the measurements, he wrote the second paper [19] as a single author, this time without his advisor’s influence. He wrote in the abstract: “That this cyclic interchange in lattice position of solute and solvent atoms in equal numbers is the only true mechanism of diffusion is denied by the evidence presented in this paper.”

Fig. 3 Metallographic observation after diffusion anneals for different times

When KIRKENDALL moved back to Wayne University, which had just been promoted to university status, there was very limited research equipment. After setting up a homemade X-ray diffraction apparatus, KIRKENDALL studied disc-shaped specimens of 15 mm in diameter (Fig. 4) consisting of Muntz metal with 60.6% copper, 0.1% total impurities, and the balance in zinc. The surface of the samples was electroplated with 5.12 mm thick copper. After the diffusion anneals, metallographic observation (Fig. 5) of a section of the specimen was performed with the optical microscope, measuring the displacement between the original interface and the α/b phase boundary. After each removal of a 200-250 mm thick layer by a lathe, the surface lattice parameter was measured by X-ray diffraction, leading to the zinc concentration profiles in the specimen.

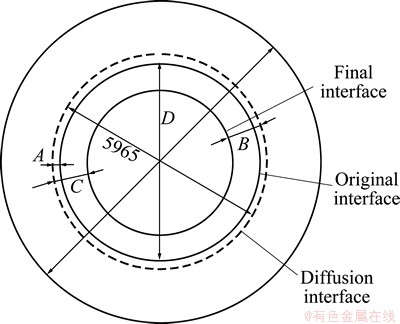
Fig. 4 Schematic of disc-shaped Muntz metal specimen used for the second paper of KIRKENDALL [19]

As seen in the metallographic observations of Fig. 5, a layer with α-brass phase was formed on both sides of the original interface. The zinc concentration profiles measured after the different anneals at 1053 K are shown in Fig. 6.

According to Fick’s first law, the diffusion mass flux (dm) across the section A in the direction of a concentration gradient (dc/dx) for the time interval (dt) can be expressed as [7]

dm=-DA(dc/dx)dt                             (1)

where D is diffusivity. Thus, one obtains

D=m/(average dc/dx)△t                       (2)

Applying Eq. (2) to the result shown in Fig. 6, the average of the diffusivity at 26% zinc concentration and 1053 K was D≈3.8×10^{-13 m2}/s. In contrast to the first paper [18] and the D.Sc. thesis, KIRKENDALL concluded with this paper that the volume shrinkage accompanied by the phase change from b- to α-brass could only explain, at most, one-fifth of the movement of the original interface. The remaining four-fifth was then attributed to the inequality of the diffusivities, with the zinc diffusion being faster than that of copper.

The second paper [19], with KIRKENDALL’s own explanation, was published in 1942. In the same year, HUNTINGTON and SEITZ [4] investigated the activation energy for self-diffusion in copper using electron theory and proposed that self-diffusion occurs by a vacancy mechanism and not by direct exchange. However, the significance of the paper was not fully recognized, and with World War II neither of the papers received enough attention. KIRKENDALL did not notice the existence of the HUNTINGTON-SEITZ paper, even after he wrote the third paper.

Fig. 5 Metallographic observation at successive diffusion anneal at 1053 K until 2523.6 ks

A few years later after the publication of the second paper, Alice SMIGELSKAS, a student, joined KIRKENDALL’s research. In his laboratory, there was only one handmade electric furnace often used for long time for diffusion annealing. SMIGELSKAS often had to manually adjust the furnace temperature sitting down beside the furnace due to malfunction of the controller. KIRKENDALL once said [7]: “In the early morning of Christmas Day she called to tell me that she could not control the furnace so as to lower the temperature. I was urged to come to my laboratory in a hurry, even though there was a heavy snowfall, leaving my wife and small children at home.”

Fig. 6 Zinc concentration profiles after different anneals at 1053 K [19]

In the experiments by SMIGELSKAS and KIRKENDALL, which led to the third paper, two main features were included. A rectangular bar (18 cm × 1.9 cm) of 70-30 wrought brass (70%Cu-30%Zn) was adopted with the purpose of avoiding the large volume change from b-brass to α-brass. Additionally, the clear observation of the movement of the original interface was achieved by inserting insoluble 130 mm molybdenum wires at the bonding interfaces between the copper and the brass. After polishing the surface of the wrought brass bar, the molybdenum wires (inert to the system) were placed on opposite surfaces, as markers. A copper layer was then deposited, as shown in Fig. 7. After annealing this couple at 785 °C for a certain time, one small piece was cut for cross-section examination and the remaining was further annealed in order to get specimens at different annealing times. With annealing, α-brass grows in between and after etching, the distance between the molybdenum wire markers was measured.

Fig. 7 Schematic representation of cross-section of diffusion couples prepared by SMIGELSKAS and KIRKENDALL [6]

before and If the diffusivities of copper and zinc are the same and there is no change in volume during the diffusion/ after annealing at 785 °C (Molybdenum wires moved closer to each other with increasing annealing time) reaction, marker should not move from the original position. However, SMIGELSKAS and KIRKENDALL’s measurements clearly showed that the distance between the markers decreases parabolically with increasing annealing time. Again, considering the change in the lattice parameter, only one-fifth of the displacement could be attributed to the molar volume change. The movement of the markers from their original positions was explained by KIRKENDALL as [6]: “The movement of the insoluble molybdenum wire was conclusive evidence that the alpha brass was being forced back as a whole (or attracted back) as a result of the diffusing out of the zinc atoms individually”.

Two main conclusions were drawn from this study, which had great impact on the understanding of solid-state diffusion at that time. First, the rate of diffusion of zinc is much greater than that of copper in alpha brass; and second, the interface shifts to compensate at least partially for the differences in diffusion rate. If, as was believed at that time, diffusion in the solid-state occurs by direct exchange or ring mechanisms, the diffusivities of the two elements should be the same. However, from the KIRKENDALL’s experiment, it was evident that the movement of the markers results from the fact that Zn diffuses faster than Cu. Due to the faster zinc diffusion, not all sites are occupied by the flow of Cu from opposite direction and, therefore, there should be a flow of vacancies opposite to the faster diffusing Zn to compensate for the difference between the Zn and Cu flux. Vacancies will then flow towards the brass side while excess Zn will diffuse towards the Cu-side. In the end, this results into shrinking in the brass side and swelling in the copper side, leading to the movement of the markers to the brass side.

Considering a similar analysis to that described in the second paper [19], the interdiffusion coefficient was evaluated from the diffusion penetration profiles obtained by SMIGELSKAS and KIRKENDALL [6], as D≈ 4×10^{-13 m2}/s, which was in good agreement with the previous value 3.8×10^{-13 m2}/s. Good reproducibility had therefore been confirmed. Moreover, the fact that zinc diffusing into the copper was faster than copper diffusing into the brass was also confirmed by the metallographic observations.

In some diffusion reactions, pores can indeed be found in the product phase [20-22]. If there is no enough plastic relaxation during the process, vacancies will coalesce to form pores or voids in the reaction layer. From KIRKENDALL’s experiments, it was clear that diffusion occurs by a vacancy mechanism and after that the direct exchange and ring mechanisms were abandoned. At first, this work was highly criticized but later this phenomenon was confirmed from experiments on many other systems [23].

The impact of KIRKENDALL’s work can be realized from MEHL’s [24] comment on his work: “If verified, this “Kirkendall effect” would greatly modify not only the treatment of diffusion data but also the theory of mechanism of diffusion. It would, for example, be no longer possible to represent diffusion data in a substitutional solid solution by one coefficient, applying to both metal atoms since the separate coefficients are equal, but one would have to show two coefficients, one each for each of the two metal atoms.”

From 1947 to 1965, KIRKENDALL was appointed secretary of the American Institute of Mining and Metallurgical Engineers (AIME) and became a manager at the United Engineering Trustees. He concluded his career in 1979 after being a vice-president of the American Iron and Steel Institute since 1966. KIRKENDALL did not attribute much significance to his discovery, at least in the forties. Many colleagues tried to persuade him to stay at the university, but he preferred the administrative job from an economy point of view. Additionally, if he had accepted the promotion to associate professor (1946) and stayed at Wayne University, he would not have any positive prospects for his research because of insufficient research facilities.

A successful meeting that illustrates the importance of KIRKENDALL’s discovery, named the Kirkendall Effect Symposium on Interdiffusion and Phenomena that Depend on Net Vacancy Flows, was held during the The Minerals, Metals and Materials Society (TMS) Fall Meeting in October 1991. This meeting was attended by Professors TURNBULL, BALLUFFI, HUNTINGTON, CAHN, HEUMANN, and many others who had contributed significantly to the understanding of lattice defects and solid-state diffusion.

3 Present understanding of Kirkendall effect

The Kirkendall effect is seen as the most explicit evidence of the occurrence of a vacancy mediated mechanism in diffusion processes in solids.  Since its discovery in 1947 [6], followed by the analysis by DARKEN in 1948 [25], the subject played a major role in the diffusion theory, being treated in all textbooks on solid-state diffusion. However, the rationalization and description of the Kirkendall effect is by no means as simple as it looks at first sight. Sometimes researchers noticed a peculiar behaviour of inert markers, when studying solid-state diffusion in different systems, which questioned the uniqueness of the Kirkendall plane, marked by the inert particles at the original interface. For example, CARTER [26] was surprised to find the split up of molybdenum wire, used as inert marker at the Al₂O₃/MgO-gas interface to study reaction and diffusion in MgAl₂O₄-spinel. When studying interdiffusion in the Ti-Ni system, BASTIN and RIECK [27] had the same experience, as shown in Fig. 8, where ThO₂ particles were split and embedded in two different phases. SHIMOZAKI et al [28] observed during study of diffusion in the b′-AuZn phase that, after interaction, the tungsten wire (which was placed at the interface of Au/g-AuZn₂ (64% Zn (mole fraction)) couple) and the original interface, revealed by traces of the joining plane, were located at two different planes. If the Kirkendall plane is unique, they should be at the same plane after annealing.

Fig. 8 Backscattered electron image of Ni/Ti diffusion couple annealed at 850 °C for 196 h [29]

However, these observations were not identified by any of the authors as indications of multiple Kirkendall planes. In the mean time, CORNET and CALAIS [30] described hypothetical diffusion couples of a binary system, where more than one “Kirkendall marker plane” may be present. Later, van LOO et al [31] further elaborated on the prediction of this phenomenon in multiphase diffusion couples. In the last few years, several systematic studies on the microstructural stability of the Kirkendall plane were performed and experimental evidence of the occurrence of multiple Kirkendall planes in a diffusion couple was found [29,32,33]. The ideas of CORNET and CALAIS were validated and a number of fundamental concepts related to the Kirkendall effect were reconsidered.

It was shown that in a volume-diffusion controlled interaction the Kirkendall plane can be multiple, stable or unstable. To evaluate these phenomena, a basic framework was formulated, in terms of velocity curve construction [32,33].

Considering the case of a diffusion couple in a generic binary A-B system, the velocity of the inert markers is dependent on the difference in intrinsic diffusivities of the species and the concentration gradients developing in the interdiffusion zone [25].

   (3)

where V_i is the partial molar volume of component i (m³/mol), J_i is the intrinsic flux of the species (mol·m²/s), D_i is the intrinsic diffusion coefficient (m²/s), C_i is the concentration of component i (mol/m³) and x is the position parameter (m). The velocity in a diffusion zone can be determined from the knowledge of intrinsic diffusivities at all compositions over the whole homogeneity range and with the help of the concentration gradient at the position of these markers in a particular diffusion couple.

In a diffusion-controlled interaction, the inert markers positioned at the location of the original interface between the reactants (Kirkendall plane) are the only markers that stay at a constant composition during the whole diffusion annealing and move parabolically in time with a velocity

                 (4)

where x_k and x₀ (=0) are the positions of the Kirkendall plane at times t=t and t=0, respectively [30].

The position(s) of Kirkendall plane(s) can be found at the point of intersection(s) between the velocity curve 2tn vs x (calculated by Eq. (3)) and the straight line 2tv_k=x_k (determined by Eq. (4)). It was shown that the nature of the Kirkendall plane(s) in a diffusion zone depends on the gradient of the velocity curve at the point of intersection. When the straight line intersects the velocity curve at a point, where _k≤0, one should expect the presence of a stable Kirkendall plane. When the gradient at the point of intersection, >0, it will result into an unstable Kirkendall plane.

Let’s now consider a hypothetical diffusion couple of alloys of A and B (A_yB_1-y/A_zB_1-z where y>z), where in the A-rich side of the diffusion zone A is the faster diffusing species, whereas in the B-rich side B is the faster diffusing species. Figure 9 shows a schematic representation of the velocity curves in different situations. In certain diffusion couples, the straight line 2tn_k=x_k may intersect the velocity curve of 2tn vs x in the diffusion zone once at a point with a negative gradient (Fig. 9(a)). At the point of intersection, the presence of one stable Kirkendall plane may be expected. Markers, which by some perturbation end up at a position slightly ahead of the Kirkendall plane, will have lower velocity and if these markers are behind this plane, they will move faster. This means that the stable Kirkendall plane acts as attractor to the inert markers. On another situation, by changing the end-member compositions, the straight line 2tn_k=x_k might intersect the velocity curve 2tn vs x at a point with a positive velocity gradient, as shown in Fig. 9(b), and an unstable Kirkendall plane may be found. The markers slightly ahead of this plane will move faster, whereas markers slightly behind this plane will move slower. The result will be scatter of the markers and no particular unique plane as the Kirkendall plane. Another possible situation is shown in Fig. 9(c), where the straight-line intersects the velocity curve three times at K₁, K₂ and K₃. In this case, three Kirkendall planes will be present, but in reality only two stable Kirkendall planes may be observed. The unstable Kirkendall plane is situated between two stable Kirkendall planes and the stable planes will accumulate all the markers during the initial stages of the interdiffusion.

Fig. 9 Schematic velocity diagrams in different conditions

Experimental evidence of the presence of stable and unstable Kirkendall planes were verified in Ni/Pd and Fe/Pd diffusion couples [29], respectively, with the help of the velocity diagram construction, as shown in Figs. 10 and 11, determined by multifoil experiments. It was indeed observed that a stable Kirkendall plane is present when the straight line 2tn_k=x_k intersects the velocity curve 2tn vs x at a point with a negative gradient. On the other hand, an unstable Kirkendall plane was found when the gradient was positive at the point of intersection.

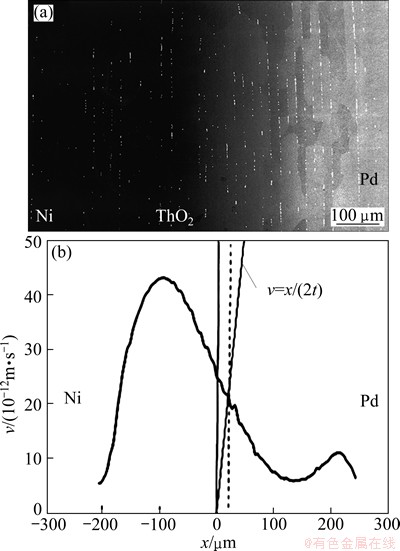
Fig. 10 Backscattered electron image of Ni/Pd couple annealed at 1100 °C for 121 h (a), Kirkendall velocity construction regarding this Ni/Pd couple (b) (adapted from Ref. [29])

Fig. 11 Backscattered electron image of Fe/Pd couple annealed at 1100 °C for 144 h (a), Kirkendall velocity construction pertaining to this Fe/Pd couple (b) (adapted from Ref. [32])

In order to verify the experimental findings by SHIMOZAKI et al [28] and in the quest for finding examples as discussed in Fig. 9, the growth of b′-AuZn phase from different Au-Zn end-members was re-examined [33]. With changing the end-member compositions, stable and unstable planes as well as the bifurcation of the Kirkendall plane were found in different diffusion couples, as shown in Figs. 12-14. Since the intrinsic diffusion coefficients as a function of composition for the b′-AuZn phase are not known, it is not possible to produce quantitative results to construct velocity diagrams in these cases.

Fig. 12 Backscattered electron image of diffusion couple grown between end-members Au₃₆Zn₆₄ (g-phase) and Au₆₆Zn₃₄ ((Au, Zn)-solid solution+b ′-AuZn) (500 °C, 17 h; Ar+5% H₂ (volume fraction)) (Only one Kirkendall plane is present in diffusion zone) (adapted from Ref. [33])

As briefly exposed, since the pioneering findings of Kirkendall, progress in the understanding of the Kirkendall effect was accomplished [34,35]. Although bifurcation of the Kirkendall plane in a single-phased diffusion zone (b′-AuZn) was explained qualitatively [33], the construction of the velocity curve based on the experimental results was not possible. There was also the question as to whether occurrence of more than two Kirkendall planes is possible in a diffusion zone [36-38]. The bifurcation and trifurcation of the Kirkendall plane need to be rationalized in order to predict their occurrence [39]. Although the behaviour of the Kirkendall plane can be successfully explained by a diffusion-based methodology making use of the velocity diagram construction [32,33], such approach is not sufficient to account for the reactions involved in a multiphase diffusion zone and for the morphological evolution during interdiffusion. Therefore, a physico- chemical approach needs to be considered for this purpose [40].

Fig. 13 Backscattered electron image of diffusion couple grown between end-members Au₄₀Zn₆₀ (b ′+g-phase) and Au₇₀Zn₃₀ ((Au, Zn)-solid solution) (500 °C, 6 h; Ar+5% H₂ (volume fraction)) (a), microstructure shown in the vicinity of array of ThO₂-particles (B in (a)) and unreacted initial end-members much further away (b) (The presence of an unstable Kirkendall plane was found in the diffusion zone) (adapted from Ref. [33])

Fig. 14 Backscattered electron image of diffusion couple grown between end-members Au and Au₃₆Zn₆₄ (g-AuZn₂) (500 °C, 17.25 h; Ar+5% H₂ (volume fraction)) (Two Kirkendall planes are present in the diffusion zone) (adapted from Ref. [33])

The interactions in Ni-Al, Cu-Sn, Ni-Sn, Au-Sn, Ni-Zn binary systems, among others, are important both for scientific understanding and for technological applications in modern energy and electronics industry. The theories on the diffusion couple technique [41-43] and Kirkendall effect briefly described here, which are scattered throughout the literature, clearly confirm the importance of KIRKENDALL’s discovery in various processes such as recrystallisation, precipitation, metallization, and oxidation, which occur in binary and more complex solid-state systems [44-60].

4 Conclusions

KIRKENDALL’s short scientific career produced one great discovery. His experiments revealed the effect of the inequality of diffusivities on the movement of the original interface on diffusion couples (named the Kirkendall effect) and showed that diffusion processes occur by a vacancy mediated mechanism. His findings played a major role in the understanding of solid state diffusion processes. More recently, further developments in the understanding of the Kirkendall effect in solid-state diffusion were achieved, which motivated this short review.

The behaviour of the Kirkendall plane can be explained by a diffusion-based framework by means of the velocity diagram construction. However, the clarification of the reactions involved in a multiphase diffusion zone and on the morphological evolution during interdiffusion requires the consideration of a physico-chemical approach.

Recent fundamental and applied advances in the field of solid-state systems and their applications, namely in energy and electronics technologies, have been attained thanks to the Kirkendall’s discovery and its impact on the understanding of complex processes such as recrystallisation, precipitation, metallization, and oxidation.

Acknowledgements

FCT, the Portuguese Foundation for Science and Technology, is gratefully acknowledged for funding project (PTDC/SEN-ENR/121265/2010) and L. AMARAL thanks for a research grant within this project.

References

[1] ROBERTS-AUSTEN W C. On the diffusion of metals [J]. Philosophical Transactions of the Royal Society A, 1896, 187: 383-415.

[2] SEQUEIRA C A C. Role of solid state chemistry in high temperature corrosion [J]. Chemical Engineering Research and Design, 2013, 91: 318-324.

[3] PFEIL L B. The oxidation of iron and steel at high temperatures [J]. Journal of the Iron and Steel Institute, 1929, 169: 501-547.

[4] HUNTINGTON H B, SEITZ F. Mechanism for self diffusion in metallic copper [J]. Physical Review, 1942, 61: 315-325.

[5] HARTLEY G S. Diffusion and swelling of high polymers, Part I: The swelling and solution of a high polymer solid considered as diffusion process [J]. Transactions of the Faraday Society, 1946, 46: 6-11.

[6] SMIGELSKAS A D, KIRKENDALL E O. Zinc diffusion in alpha brass [J]. Transactions of the AIME, 1947, 171: 130-134.

[7] Nakajima H. The discovery and acceptance of the Kirkendall effect: The result of a short research career [J]. JOM, 1997, 49(6): 15-19.

[8] DARKEN L S, GUSSY R W. Physical chemistry of metals [M]. New York: McGraw Hill Book Co., 1953.

[9] SHEWMON P G. Diffusion in solids [M]. New York: McGraw Hill Book Co., 1963.

[10] Kirkaldy J S, Young D J. Diffusion in the condensed state [M]. London: The Institute of Metals, 1987.

[11] Adda Y, Philibert J. Atom movements and mass transport in solids [M]. Les Ulis, Paris: Les de Physique, 1991.

[12] Alnatt A R, Lidiard A B. Atomic transport in solids [M]. Cambridge: Cambridge University Press, 1993.

[13] Glicksman M E. Diffusion in solids [M]. New York: John Wiley & Sons, Inc, 2000.

[14] Sequeira C A C. High temperature oxidation [M]//Winston Revie R. UHLIG’s Corrosion Handbook. Third edition. New York: John Wiley & Sons, Inc, 2011: 247-280.

[15] Desch C H. Report on diffusion in solids [J]. Reports of British Association for the Advancement of Science, 1912, 82: 348-372.

[16] Mehl R F. Diffusion in solid metals [J]. Transactions of the AIME, 1936, 122: 11-56.

[17] Krynitsky A I. Metals and alloys [M]. 1937: 138-144; 173-179; 261.

[18] Kirkendall E O, Thomassen L, Upthegrove C. Rates of diffusion of copper and zinc in alfa brass [J]. Transactions of the AIME, 1939, 133: 186-203.

[19] Kirkendall E O. Diffusion of zinc in alpha brass [J]. Transactions of the AIME 1942, 147: 104-110.

[20] van Dal M J H, Huibers D G G M, Lodentsov A a, van Loo F J J. Formation of Co-Si intermetallics in bulk diffusion couples. Part I: Growth kinetics and mobilities of species in the silicide phases [J]. Intermetallics, 2001, 9: 409-421.

[21] Sauer F, Freise V. Diffusion in binary mixtures with volume change [J]. Z Electrochem, 1962, 66: 352-363. (in German)

[22] Labie R, Ruy Thooren W, Humbreck J V. Solid state diffusion in Cu-Sn and Ni-Sn diffusion couples with flip-chip scale dimensions [J]. Intermetallics, 2007, 15: 396-403.

[23] da Silva L C C, Mehl R F. Interface and marker movements in diffusion in solid solutions of metals [J]. Transactions of the AIME, 1951, 191: 155-172.

[24] Mehl R F. Discussion following ref. [6] [J]. Transactions of the AIME, 1947, 171: 135-142.

[25] Darken L S. Diffusion, mobility and their intercalation through free energy in binary metallic systems [J]. Transactions of the AIME, 1948, 175: 184-201.

[26] Carter R E. Mechanism of solid-state reaction between magnesium oxide and aluminium oxide and between magnesium oxide and ferric oxide [J]. Journal of the American Ceramic Society, 1961, 44: 116-120.

[27] Bastin G F, Rieck G D. Diffusion in the titanium-aluminium system: I. Occurrence and growth of the various intermetallic compounds [J]. Metallurgical Transactions, 1974, 5: 1817-1826.

[28] Shimozaki T, Goda Y, Wakamatsu Y, Onishi M. Interdiffusion and Kirkendall effect in Au-Zn ordered b’ phase [J]. Defect and Diffusion Forum, 1993, 95-98: 629.

[29] van Dal M J H, Pleumeekers M C L P, Kodentsov A A, van LOO F J J. Intrinsic diffusion and Kirkendall effect in Ni-Pd and Fe-Pd solid solutions [J]. Acta Materialia, 2000, 48: 385-396.

[30] Cornet J F, Calais D. The study of the Kirkendall effect after Darken equations [J]. Journal of Physics and Chemistry of Solids, 1972, 33: 1675-1684. (in French)

[31] van Loo F J J, Pieraggi B, Rapp R A. Interface migration and the Kirkendall effect in diffusion driven phase transformations [J]. Acta Metallurgica et Materialia, 1990, 38: 1769-1779.

[32] van Dal M J H, Gusak A M, Cserháti C, Kodentsov A A, van Loo F J J. Microstructural stability of the Kirkendall plane in solid state diffusion [J]. Physical Review Letters, 2001, 86: 3352-3355.

[33] van Dal M J H, Gusak A M, C, Kodentsov A A, van Loo F J J. Spatio-temporal instability of the Kirkendall-marker planes during interdiffusion in b'-AuZn [J]. Philosophical Magazine A, 2002, 82: 943-954.

[34] Kodentsov A a, van Dal M J H, Cserháti C, Gusak A M, van Loo F J J. Patterning in reactive diffusion [J]. Defect Diffusion Forum, 2001, 194: 1491-1502.

[35] van Dal M J H, Gusak A M, Cserháti C, Kodentsov A A, van Loo F J j. Instability of Kirkendall planes [J]. Defect Diffusion Forum, 2001, 194: 195-200.

[36] Ugaste Y E, Kodentsov A A, van Loo F J J. Investigation of the interdiffusion and Kirkendall effect in Co-Ni-Fe system: I. Redistribution of component concentrations in the diffusion zone and shift of the inert markers [J]. Physics of Metals and Metallography, 2004, 97(3): 298-306.

[37] Svoboda J, Gamsjager E, Fischer F D, Kozeschnik E, Modelling of kinetics of diffusive phase transformation in binary systems with multiple stoichiometric phases [J]. Journal of Phase Equilibria and Diffusion, 2006, 27(6): 622-628.

[38] Boettinger W J, Guyer J e, Campbell C E, McFadden G B. Computation of the Kirkendall velocity and displacement fields in a one-dimensional binary diffusion couple with a moving interface [J]. Proceedings of the Royal Society A, 2007, 463: 3347-3373.

[39] Svoboda J, Fischer F D, Abart R. Modelling of diffusional phase transformation in multicomponent systems with stoichiometric phases [J]. Acta Materialia, 2010, 58(8): 2905-2911.

[40] Ghosh C, Paul A. Elucidation of bifurcation of the Kirkendall marker plane in a single phase using physico-chemical approach [J]. Intermetallics, 2008, 16(8): 955-961.

[41] Vassilev G P. Application of diffusion couple technique for the determination of Ti-Bi-Sn phase diagram [J]. Crystal Research and Technology, 2005, 40(7): 713-718.

[42] Xu H H, DU Y, ZHOU Y C, JIN Z P. Determination of phase diagrams using the diffusion couple [J]. Rare Metals, 2006, 25(5): 427-430.

[43] Miyamoto T, Nagasako M, Kainuma R. Phase equilibria in the Ni-Mn-In alloy system [J]. Journal of Alloys and Compounds, 2013, 549: 57-68.

[44] Glicksman M E. Diffusion in solids [M]. New York: John Wiley & Sons, Inc, 2000.

[45] Bader S, Gust w, Hieber h. Rapid formation of intermetallic compounds by interdiffusion in the Cu-Sn and Ni-Sn systems [J]. Acta Metallurgica et Materialia, 1995, 43: 329-337.

[46] GAO F, Takemoto T, Nishikawa H. Effects of Co and Ni addition on reactive diffusion between Sn-3.5 Ag solder and Cu during soldering and annealing [J]. Materials Science and Engineering A, 2006, 420: 39-46.

[47] Ghosh G. Interfacial microstructure and the kinetics of interfacial reaction in diffusive couples between Sn-Pb solder and Cu/Ni/Pb metallization [J]. Acta Materialia, 2000, 48: 3719-3738.

[48] Yamakami M, Kajihara M. Solid-state reactive diffusion between Sn and electroless Ni-P at 473 K [J]. Materials Transactions,2009, 50: 130-137.

[49] Kodentsov A A, Paul A, van DAL M J H, Cserhati C, Gusak A M, van LOO F J J. On the spatial stability and bifurcation of the Kirkendall plane during solid-state interdiffusion [J]. Critical Reviews in Solid State and Materials Sciences, 2008, 33(3-4): 210-233.

[50] Paul A, van DAL M J H, Kodentsov A A, van LOO F J J. The Kirkendall effect in multiphase diffusion [J]. Acta Materialia, 2004, 52(3): 623-630.

[51] PAUL A, van DAL M J H, Kodentsov A A, van LOO F J J. On the behaviour of Kirkendall markers in solid-state interdiffusion [J]. Archives of Metallurgy and Materials, 2004, 49(2): 259-276.

[52] PAUL A, Kodentsov A A, van LOO F J J. Bifurcation and trifurcation of a Kirkendall plane during multiphase interdiffusion [C]//Diffusion in Materials: DIMAT 2004, Pts 1 and 2. 2005, 237-240: 813-824.

[53] Paul A, Kodentsov A A, van LOO F J J. Bifurcation of the Kirkendall plane during interdiffusion in the intermetallic compound beta-NiAl [J]. Acta Materialia, 2004, 52(13): 4041-4048.

[54] Kodentsov A A, PAUL A, van LOO F J J. Bifurcation of the Kirkendall plane and patterning in reactive diffusion [J]. Zeitschrift Fur Metallkunde, 2004, 95(4): 258-260.

[55] PAUL A, Kodentsov A A, van LOO F J J. Intermetallic growth and Kirkendall effect manifestations in Cu/Sn and Au/Sn diffusion couples [J]. Zeitschrift Fur Metallkunde, 2004, 95(10): 913-920.

[56] Kodentsov A A, PAUL A, van LOO F J J. The Kirkendall plane in binary interdiffusion systems [C]//Defects and Diffusion in Metals- an Annual Retrospective Vii. 2004, 233: 61-75.

[57] PAUL A, van DAL M J H, Kodentsov A A, van LOO F J J. The Kirkendall effect in multiphase interdiffusion [J]. Defect and Diffusion Forum, 2002, 216(2): 65-72.

[58] TANG W M, HE A Q, LIU Q, IVEY D G. Solid state interfacial reactions in electrodeposited Cu/Sn couples [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(1): 90-96.

[59] WU M, QU X H, HE X B, RAFI-UD-DIN, REN S B, QIN M L. Interfacial reactions between Sn-2.5Ag-2.0Ni solder and electroless Ni(P) deposited on SiCp/Al composites [J]. Transactions of Nonferrous Metals Society of China, 2010, 20(6): 958-965.

[60] SUN Y B, ZHAO Y Q, Zhang D, LIU C Y, DIAO H Y, MA C L. Multilayered Ti-Al intermetallic sheets fabricated by cold rolling and annealing of titanium and aluminum foils [J]. Transactions of Nonferrous Metals Society of China, 2011, 21(8): 1722-1727.

固态扩散过程中的Kirkendall效应

C. A. C. SEQUEIRA, L. AMARAL

Materials Electrochemistry Group, ICEMS, Instituto Superior , Universidade de Lisbon, Avenida Rovisco Pais 1, 1049-001 Lisboa, Portugal

摘  要：在二十世纪四十年代，柯肯达尔(Kirkendall)发现，在二元固溶体中，扩散过程不能简单地用一种扩散系数来描述它，人们必须考虑到两种物质的扩散系数的不同。他的发现改变了以往的扩散理论和数据的处理方式。基于他的这种扩散理论成功解释了Kirkendall平面的行为。但是，多相扩散和扩散过程中组织形貌的演变是很复杂的，需要从物理化学的途径才能解决。从理论和工艺的角度来看，二元或多元体系中的相互作用是关键问题。本文综述了Kirkendall效应的发现以及最近的进展，及其在材料科学中的应用前景。

关键词：Kirkendall效应；Kirkendall速度；Kirkendall平面；扩散偶技术；固体扩散；相互扩散

(Edited by Sai-qian YUAN)

Corresponding author: C. A. C. SEQUEIRA; Tel: +351-218417765; E-mail: cesarsequeira@ist.utl.pt

DOI: 10.1016/S1003-6326(14)63021-1