DOI: 10.11817/j.issn.1672-7207.2016.11.036
利用多尺度形态学和递归图分离辨识大地电磁微弱信号
李晋1, 2,汤井田2,蔡剑华3,燕欢1
(1. 湖南师范大学 物理与信息科学学院,湖南 长沙,410081;
2. 中南大学 地球科学与信息物理学院,有色金属成矿预测与地质环境监测教育部重点实验室,
湖南 长沙,410083;
3. 湖南文理学院 物理与电子科学学院,湖南 常德,415000)
摘要:为了突出形态滤波中结构元素不同尺度下的相关局部特性、分层次刻画大地电磁信号本身所固有的多尺度特征,将加权多尺度形态滤波与递归图相结合对大地电磁微弱信号与噪声进行信噪分离及信噪辨识。首先,利用不同尺度的结构元素对大地电磁信号进行全方位扫描;然后,加权合成获取更精细的形态特征信息;最后,引入非线性动力学行为中的递归图对分离出的信噪特征进行确定性检验。研究结果表明:大地电磁微弱信号与噪声得到更精细分离;递归图的相空间轨迹适合定性判断大地电磁时间序列的非稳态动态变化;卡尼亚电阻率曲线更加光滑、连续,大地电磁低频段数据质量得到有效改善。
关键词:大地电磁;多尺度形态学;递归图;信噪分离;信噪辨识
中图分类号:P631 文献标志码:A 文章编号:1672-7207(2016)11-3890-09
Separation and identification of magnetotelluric weak data using multi-scale morphology and recurrence plot
LI Jin1, 2, TANG Jingtian2, CAI Jianhua3, YAN Huan1
(1. Institute of Physics and Information Science, Hunan Normal University, Changsha 410081, China;
2. Key Laboratory of Metallogenic Prediction of Non-Ferrous Metals and Geological Environment Monitor,
Ministry of Education, School of Geosciences and Info-Physics, Central South University, Changsha 410083, China;
3. Department of Physics and Electronics, Hunan University of Arts and Science, Changde 415000, China)
Abstract: In order to highlight relevant local characteristics of different scales of structural elements for morphology filtering, and depict inherent multi-scale features of magnetotelluric data hierarchically, a new method that combined weighted multi-scale morphological filtering with recurrence plot to analyze the effect of signal-to-noise separation and identification of magnetotelluric weak data was proposed. Firstly, different scales of structural elements were used to scan magnetotelluric data comprehensively. Then, the more elaborate information of morphological characteristics was obtained by weighted synthesis. Finally, recurrence plot of non-linear dynamic behavior that inspects the characteristics of signal and noise of magnetotelluric data was adopted. The results indicate that the weak signal and noise of magnetotelluric data separate more elaborately, and recurrence plots of phase space trajectory are suitable for inspecting unsteady dynamic changes of time series of magnetotelluric qualitatively. Moreover, Cagniard resistivity curve becomes more smooth and continuous, and the quality of low frequency for magnetotelluric data is improved effectively.
Key words: magnetotelluric; multi-scale morphology; recurrence plot; signal-to-noise separation; signal-to-noise identification
大地电磁测深法(magnetotelluric,简称MT法)自20世纪50年代被提出,如何消除大地电磁信号中的噪声干扰、提高大地电磁测深质量成为人们研究的重 点[1]。VOZOFF[2]从大地电磁场的基本关系出发,在傅里叶谱分析的基础上提出最小二乘法,得到6种计算阻抗张量要素的算法。KAO等[3]提出利用互功率谱和由4种阻抗估算得到自功率谱的平均值重新估算阻抗的方法。GAMBLE等[4]提出完全不用自功率谱而仅用互功率谱进行阻抗估算的方法,随后又提出远参考道大地电磁测深法,消除非相关噪声。EGBERT等[5]通过分析大地电磁资料的误差分布规律,提出了Robust的大地电磁阻抗张量估算方法。随着信息技术的飞速发展,诸多现代信号处理方法被应用到大地电磁噪声压制中。TRAD等[6]利用小波域的不同尺度对大地电磁数据进行噪声压制,并采用Robust法估算阻抗。汤井田等[7]提出将Hilbert-Huang变换应用到电法勘探,并成功运用经验模态分解对大地电磁信号矫正基线漂移及压制工频干扰。景建恩等[8]研究了基于广义S变换的大地电磁测深数据处理方法,在时频域通过增加频谱系数的个数,改善了大地电磁阻抗张量的估算质量。KAPPLE[9]提出了一种通过方差比识别噪声、利用维纳滤波滤除脉冲噪声的方法,提高了低频段的大地电磁数据质量。王辉等[10]研究了同步大地电磁时间序列依赖关系的噪声处理方法,结合参考道的数据合成了本地道含噪时段的新数据,有效地抑制了中高频段的近场效应。上述方法均在一定程度上对大地电磁测深数据质量起到了改善作用。但由于电磁噪声的复杂性以及人类社会、经济活动的加剧,人文电磁噪声日趋严重,使得野外观测数据的重复性和一致性变差,曲线参数的抗干扰能力也逐渐降低。随着我国深部探测技术与实验研究专项的深入,不可避免地需要在长江中下游成矿带及典型矿集区开展大地电磁探测工 作[11]。矿集区中各种复杂的电磁干扰源严重污染了实际大地电磁信号,引起大地电磁阻抗估算偏差严重及测量获得的视电阻率过度失真等状况,导致不能客观反映地下电性分布,甚至得到错误的解释结论[12]。由于矿集区实测大地电磁噪声干扰的频谱通常分布在宽频带甚至是全频带范围内,导致现有的频率域去噪方法对该类强噪声干扰失效。针对上述一系列不利因素及实际情况,汤井田等[13-14]围绕大地电磁信号和强干扰的时间域波形特征,运用数学形态滤波开展噪声压制研究。然而,现有的数学形态滤波方法(传统方法、广义方法)在压制大地电磁噪声干扰时采用的是固定尺度的结构元素,导致在保留细节信息和提取轮廓特征上不能真实反映大地电磁信号本身所固有的多尺度特征。为此,本文作者在前期研究基础上,提出一种加权多尺度形态滤波的大地电磁信噪分离方法,并引入非线性动力学分析中的递归图法,对不同时间尺度的大地电磁时间序列的动力学行为进行信噪辨识和确定性检验。
1 多尺度形态滤波和递归图
1.1 多尺度形态学
人的感知是一个由粗到精的分层次处理过程。首先获取大范围的轮廓进行粗略判断,然后捕捉相关细节使得分析过程越来越精细,最后精确理解感知对象。客观世界都具有多层次特性,仅仅在某一固定的模式下分析信号,不能表现出信号本身所固有的多尺度、多分辨特征,同时也限制了分析结果的准确性。数学形态学中的结构元素对信号特征提取起关键作用,一种给定参数的结构元素一般仅与某一类典型的待处理信号达到最优匹配效果。因此,当待处理信号中包含复杂成分时,传统形态滤波显然不能达到预期效果。融合多尺度运算和数学形态学衍生了多尺度形态学的概念,即在传统形态滤波中引入了结构元素“尺度”这个特性,相当于用不同的尺子度量同一目标,通过对信号的形态进行多尺度刻画,以便对处理信号的几何特征进行不断局部匹配及修正。多尺度形态学分析已成功应用于机械故障诊断、地震资料处理等领域[15-16]。
假设T为形态学变换,X为信号,基于T的多尺度形态学变换为一簇形态学变换 。其中:
。其中:
 ;s>0 (1)
;s>0 (1)
以一维离散信号为例,多尺度形态学的数学描述如下:
设输入信号 为定义在
为定义在 上的离散函数,结构元素
上的离散函数,结构元素 为定义在
为定义在
 上的离散函数,且N >> M,则
上的离散函数,且N >> M,则 关于
关于 的多尺度形态腐蚀和膨胀运算分别定义为[17]:
的多尺度形态腐蚀和膨胀运算分别定义为[17]:
 ;
;
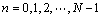 (2)
(2)
 ;
;
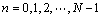 (3)
(3)
式中: 和
和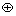 分别表示形态学中的腐蚀和膨胀运算;sg由g经过s-1次自身膨胀得到,表示s尺度下的结构元素,
分别表示形态学中的腐蚀和膨胀运算;sg由g经过s-1次自身膨胀得到,表示s尺度下的结构元素,
 (4)
(4)
将多尺度形态腐蚀和膨胀级联组成最基本的多尺度形态开、闭滤波器:
 ;
;
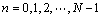 (5)
(5)
 ;
;
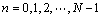 (6)
(6)
式中:符号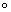 和
和 分别表示形态学中的开和闭运算。将上述多尺度形态开、闭运算级联,定义多尺度形态学中的开-闭(MOC)和闭-开(MCO)滤波器如下:
分别表示形态学中的开和闭运算。将上述多尺度形态开、闭运算级联,定义多尺度形态学中的开-闭(MOC)和闭-开(MCO)滤波器如下:
 ;
;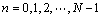 (7)
(7)
 ;
;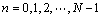 (8)
(8)
1.2 加权多尺度形态滤波器构建
为了克服传统形态滤波在保留信号细节信息和提取轮廓特征上的不足,考虑到小尺寸的结构元素去噪能力弱,但能保留较好的信号细节,大尺寸的结构元素去噪能力强,但会模糊信号的边界,不同尺度的结构元素对不同形状的信号具有不同的适应性,结合上述多尺度形态学的思路,构建一种加权多尺度形态滤波器。
假设结构元素的尺度范围为 ,可得到k个有效尺度下的各阶信号:
,可得到k个有效尺度下的各阶信号:
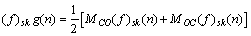 ;
;
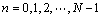 (9)
(9)
运用多尺度加权合成得到最终的处理信号:
 (10)
(10)
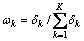 ;
; (11)
(11)
式中: 为各尺度信号的权重因子;
为各尺度信号的权重因子; 为不同尺度下形态滤波差值的标准差。加权多尺度形态滤波的基本思想是在提取信号几何形态的同时,利用不同尺度的结构元素对待处理信号进行全方位扫描,从而获取更精细的形态特征信息。
为不同尺度下形态滤波差值的标准差。加权多尺度形态滤波的基本思想是在提取信号几何形态的同时,利用不同尺度的结构元素对待处理信号进行全方位扫描,从而获取更精细的形态特征信息。
1.3 递归图
随着非线性动力学理论的日益深入,人们试图提取非线性时间序列中的非线性特征量进行信噪辨识。由于一维时间序列维数受限,不足以体现信号的内在特性。为了获取一维时间序列中更多的有用信息,通过合理地选取数据段、扩展序列的维数及采用一定的算法构造若干向量的二维矩阵,并将能够反映信号内在特性的信息体现在二维图形上,导致递归图(recurrence plot,RP)的产生[18]。递归图是一种非线性动力学分析方法,主要用于分析时间序列的周期性、非平稳性和混沌性。它以相空间重构为基础,揭示时间序列的内部结构,反映恢复后的混沌吸引子所具有的某种规律和信号演变过程中的特点;不同性质的信号其轨迹状态的特征不一样,表现在递归图的结构上也不相同[19]。
对于N点时间序列 重构m维相空间,可得到时间序列暗含的动力学系统
重构m维相空间,可得到时间序列暗含的动力学系统 :
:
 (12)
(12)
式中: 为时间延迟;m为嵌入维数。在相空间重构的基础上,递归值
为时间延迟;m为嵌入维数。在相空间重构的基础上,递归值 定义为
定义为
 (13)
(13)
式中: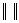 表示Euclidean范数,用来计算重构相空间中所有行向量Yi与列向量Yj之间的欧式距离;
表示Euclidean范数,用来计算重构相空间中所有行向量Yi与列向量Yj之间的欧式距离;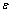 为邻域半径,其选取范围一般为待处理信号标准差的15%;
为邻域半径,其选取范围一般为待处理信号标准差的15%; 为Heaviside函数,
为Heaviside函数,
 (14)
(14)
通过上述步骤便将一维时间序列重构成m维的相空间轨迹,从动力学系统上实现了在高维空间恢复吸引子。当2个相点之间的距离小于某一选取的领域半径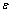 时,表示这2点之间的距离是递归的,用1个黑点(
时,表示这2点之间的距离是递归的,用1个黑点(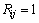 )来表示,否则就是不递归的,用1个白点(
)来表示,否则就是不递归的,用1个白点(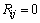 )或空格来表示。通过研究这些黑、白点的分布情况,在拓扑等价意义下可获得原系统的动力学特性。
)或空格来表示。通过研究这些黑、白点的分布情况,在拓扑等价意义下可获得原系统的动力学特性。
2 理论信号仿真试验
2.1 EMTF仿真试验信号
国内外大地电磁学者广泛使用的EMTF开源代码包主要是针对大地电磁时间序列进行阻抗估计及远参考分析。为了将EMTF开源代码提供的100 Ω·m均匀半空间的时间序列(1 Hz采样)视为理论信号进行研究,在Window环境下重新编译EMTF开源代码包,并与SSMT进行阻抗估算的分析对比。考虑到大地电磁噪声类型极复杂,仿真试验仅选用矿集区中普遍存在的方波干扰进行讨论。这种方式为后续实测数据处理奠定了基础,同时也避免了仪器差异、布极方式、标定文件及天然场变化等带来的不确定因素。
图1所示为EMTF中的理论电道信号Ex时间片段及添加幅值百分比为200%、宽度为500、间距为800的仿真方波。从图1可知:当理论信号中添加仿真方波干扰后,理论信号几乎被大尺度、强能量的方波噪声所湮没,仿真试验信号中的主要波形特征表现为方波干扰。
2.2 多尺度形态滤波性能分析
为了探讨结构元素尺度的滤波效果,将图1所示的Ex信号添加仿真方波作为测试信号进行加权多尺度形态学的仿真试验,通过对比分析去噪前后的曲线相似度和信噪比来综合评价结构元素尺度的去噪性能。曲线相似度NCC定义如下:
 (15)
(15)
式中:N为数据总长度; 为原始信号的幅值;
为原始信号的幅值;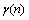 为去噪后差值信号的幅值。信噪比RSN的定义如下:
为去噪后差值信号的幅值。信噪比RSN的定义如下:
 (16)
(16)
式中: 为形态滤波输出信号的幅值。由于干扰类型单一,选用不同类型的结构元素对形态滤波的效果并不敏感,为此,文中的传统形态滤波均采用单位尺度结构元素(
为形态滤波输出信号的幅值。由于干扰类型单一,选用不同类型的结构元素对形态滤波的效果并不敏感,为此,文中的传统形态滤波均采用单位尺度结构元素( )进行研究,多尺度分析则在单位尺度上进行延拓。图2所示为测试信号经传统形态滤波、多尺度形态滤波和加权多尺度形态滤波的仿真效果图。
)进行研究,多尺度分析则在单位尺度上进行延拓。图2所示为测试信号经传统形态滤波、多尺度形态滤波和加权多尺度形态滤波的仿真效果图。
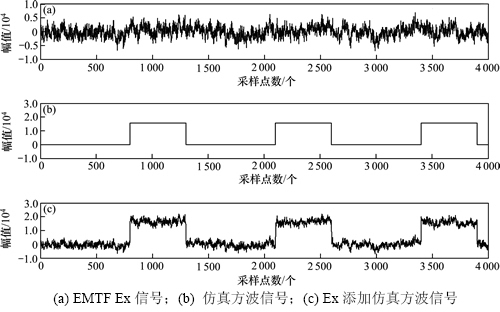
图1 Ex (EMTF)添加仿真方波
Fig. 1 Ex (EMTF) added simulation square waveforms

图2 形态滤波仿真效果图
Fig. 2 Simulation effects of morphological filtering
图2中的加权多尺度形态滤波采用了尺度在3~100之间平均分配的9个尺度即3,13,24,35,46,56,67,78和89的结构元素进行合成分析。从图2可知:传统形态滤波由于结构元素尺度的固定性,提取的噪声形态轮廓显然不能体现其他刻度下的细节信息;多尺度形态滤波由于选取不同尺度下的结构元素进行多层次分析,尺子的刻度不一样导致提取轮廓特征的精细程度也不尽相同,当尺度为105(大于噪声宽度的0.2倍)时,提取的形态轮廓出现明显失真;加权多尺度形态滤波将有效尺度范围内的大、小尺度进行结合,提取的波形轮廓更加光滑、连续。仿真结果进一步说明了方法的分层次刻画性能,突出了各尺度下信号的相关局部特性,并更精细地反映了信号本身所固有的形态结构特征,为全方位扫描待处理信号提供了可能。对比传统形态滤波和本文所提方法,曲线相似度由0.986 1提升至0.995 9,信噪比由15.093 7 dB提升至20.568 5 dB,这2个参数均得到了明显提高。
2.3 递归图定性评价
图3所示为理论信号、测试信号、传统形态滤波和加权多尺度形态滤波处理后的递归图。
从图3可知:理论信号反映在递归图中的黑、白点均匀分布,递归图几乎毫无规律,时间序列变得无法预测,符合天然大地电磁信号是随机分布的特征。测试信号中由于人为地添加了大尺度方波干扰,黑点和白点则呈现出很有规则的图形,且分布在与主对角线平行的直线两侧,从递归图的动力学机理可以解释为信号所包含的确定性和可预测性比随机系统中的随机序列更加明显。传统形态滤波的递归图虽然黑、白点的分布有所分散,但从一些与对角线平行的条带中可以发现轨迹的变化趋势具有一定的类周期性,说明去噪并不充分,导致滤波后仍含有方波干扰的某些特性,从而呈现出一定的规则图案。观测加权多尺度形态滤波的递归图可知,黑、白点的分布均匀、趋近随机状态,且递归图中没有呈现规则的图案,这在一定程度上可以认为滤波后的信号其变化趋势已逐渐逼近于理论信号的原始特征。
图4所示为理论信号、测试信号、传统形态滤波和加权多尺度形态滤波处理后的时频谱图。
分析图4可知:经加权多尺度形态滤波处理后的信号其频谱形态基本恢复为理论信号的形态特征。传统形态滤波由于尺度单一、滤波不彻底,导致频谱幅值在某些频段明显集中。

图3 大地电磁信号递归图
Fig. 3 Recurrence plots of magnetotelluric data

图4 大地电磁信号时频谱图
Fig. 4 Spectrograms of magnetotelluric data
3 实测数据处理
3.1 时间域滤波效果
图5和图6分别所示为采用传统形态滤波、加权多尺度形态滤波对庐枞矿集区某测点实测大地电磁信号Ex分量的时间域和递归图的仿真效果。
对比分析图5和图6可知:传统形态滤波获取的强干扰轮廓整体趋势并不光滑,递归图中黑、白点分布也不随机,反映在相空间递归点的递归频率明显增大;本文所提方法由于结构元素在有效尺度范围内进行加权多尺度选取,提取的信号包含了全方位、分层次的结构信息,获得的强干扰的形态轮廓连续、平滑,突出了大地电磁有用信号的相关局部特性;递归图中的黑、白点分布更加分散,反映在相空间轨迹的聚集度明显减弱,说明重构的大地电磁信号所包含的随机性增强,大地电磁微弱信号中更丰富的细节成分得到保留。
3.2 卡尼亚电阻率曲线
图7所示为矿集区某测点的大地电磁原始数据卡尼亚电阻率曲线。从图7可知:原始数据的卡尼亚电阻率曲线整体形态连续性差,视电阻率极不稳定;在大于5 Hz及0.005~0.050 Hz处,曲线形态较平稳;在0.5~5 Hz处,视电阻率从1 000Ω·m下降到100Ω·m后立即呈45°左右渐近线快速上升至1 000Ω·m;在0.05~0.50 Hz处,视电阻率从1 000Ω·m下降至10Ω·m以下,然后急剧上升接近于10 000Ω·m,视电阻率变化异常紊乱,数值变化超过3个数量级;在0.000 5~ 0.005 0 Hz处的甚低频段,视电阻率跳变非常剧烈,误差棒明显增大,这些现象均表明该测点数据受到了矿集区强噪声的干扰。

图5 Ex分量时间域波形滤波效果
Fig. 5 Filtering effect of time-domain waveform for Ex component
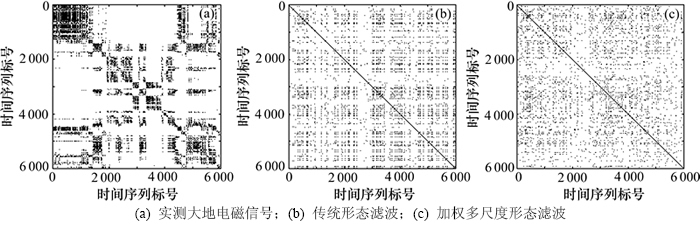
图6 Ex分量递归图滤波效果
Fig. 6 Recurrence plots of Ex component

图7 原始数据卡尼亚电阻率曲线
Fig. 7 Cagniard resistivity curve of original magnetotelluric data
图8所示为原始测点数据经传统形态滤波、本文所提方法及在本文所提方法上经简单的功率谱筛选获得的卡尼亚电阻率曲线。
分析图8(a)和图8(b)可知:由于形态滤波(传统、本文)能剔除大尺度干扰,0.05~0.50 Hz 处的近源干扰及跳变剧烈现象已基本消除;在频率大于0.005 Hz处,除了0.1 Hz左右出现1个飞点外,视电阻率趋于平稳。然而,因为传统形态滤波中结构元素尺度选取单一,在提取强干扰的同时也滤除了其他尺度中大地电磁有用信号的低频细节成分,导致0.000 5~0.005 0 Hz处反映深部构造信息的低频段数据呈脱节现象,且曲线变得紊乱、误差棒增大。本文所提方法由于全方位地考虑了大地电磁信号本身所固有的多尺度特征,因而更精细地保留了有用信号的细节成分,表现在0.000 5~0.005 0 Hz频段除最后1个频点数据下降外,其他频点的数据均有明显抬升,曲线形态较传统形态滤波更平稳、光滑,整体连续性大大提高,误差显著降低。在图8(b)的基础上仅对0.1 Hz左右的飞点和最后1个频点进行功率谱筛选,获得如图8(c)所示的卡尼亚电阻率曲线。分析图8(c)可知:该测点经本文所提方法处理后仅需通过简单的功率谱筛选即可获得更加光滑、连续的卡尼亚电阻率曲线。
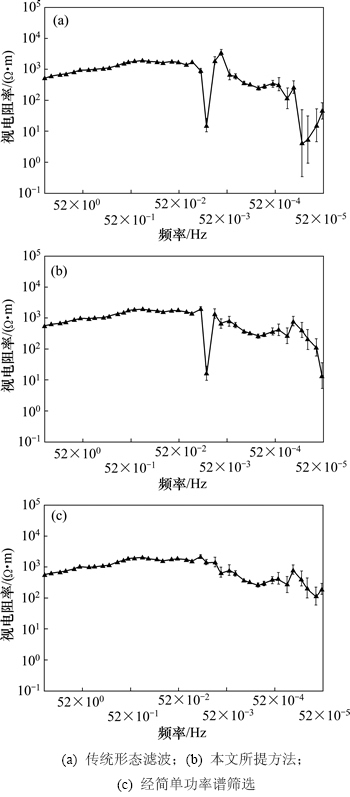
图8 处理后的卡尼亚电阻率曲线对比
Fig. 8 Comparison of Cagniard resistivity curve after processing
4 结论
1) 加权多尺度形态滤波利用不同尺度的结构元素对大地电磁信号进行全方位扫描,与传统形态滤波相比在时间域获取了更精细的形态特征信息,突出了信号各尺度下的相关局部特性;卡尼亚电阻率曲线仅需简单的功率谱筛选即可更光滑、连续,视电阻率相对稳定,其结果为地下电性结构的解释提供了更加可靠的依据。
2) 递归图从动力学角度揭示了大地电磁时间序列相空间轨迹的运行方式,能对其确定性成分的存在和周期性成分的嵌入进行精细刻画。该方法获取了系统的全局相关信息,能定性判断大地电磁时间序列的非稳态动态变化,适合对大地电磁测深数据进行信噪辨识和确定性检验。
3) 所提方法突破了传统形态滤波中结构元素尺度选取的固定性,为今后在矿集区开展大地电磁勘探及建立鉴定大地电磁信噪分离和信噪辨识评价准则提供了新的研究思路,具有潜在的应用价值。由于实测大地电磁测深数据面临复杂多样的噪声干扰环境,建议对结构元素尺度的自适应选取进行进一步研究。
参考文献:
[1] CHEN J, HEINCKE B, JEGEN M, et al. Using empirical mode decomposition to process marine magnetotelluric data[J]. Geophysical Journal International, 2012, 190(1): 293-309.
[2] VOZOFF K. The magnetotelluric method in the exploration of sedimentary basins[J]. Geophysics, 1972, 37(1): 98-141.
[3] KAO D W, RANKIN D. Enhancement of signal-to-noise radio in magnetotelluric data[J]. Geophysics, 1977, 42(1): 103-110.
[4] GAMBLE T D, GOUBAN W M, CLARKE J. Magnetotellurics with a remote magnetic reference[J]. Geophysics, 1979, 44(1): 53-68.
[5] EGBERT G D, BOOKER J R. Robust estimation of geomagnetic transfer functions[J]. Geophysical Journal International, 1986, 87(1): 173-194.
[6] TRAD D O, TRAVASSOS J M. Wavelet filtering of magnetotelluric data[J]. Geophysics, 2000, 65(2): 482-491.
[7] 汤井田, 化希瑞, 曹哲民, 等. Hilbert-Huang变换与大地电磁噪声压制[J]. 地球物理学报, 2008, 51(2): 603-610.
TANG Jingtian, HUA Xirui, CAO Zhemin, et al. Hilbert-Huang transformation and noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics, 2008, 51(2): 603-610.
[8] 景建恩, 魏文博, 陈海燕, 等. 基于广义S变换的大地电磁测深数据处理[J]. 地球物理学报, 2012, 55(12): 4015-4022.
JING Jianen, WEI Wenbo, CHEN Haiyan, et al. Magnetotelluric sounding data processing based on generalized S transformation[J]. Chinese Journal of Geophysics, 2012, 55(12): 4015-4022.
[9] KAPPLE K N. A data variance technique for automated despiking of magnetotelluric data with a remote reference[J]. Geophysical Prospecting, 2012, 60(1): 179-191.
[10] 王辉, 魏文博, 金胜, 等. 基于同步大地电磁时间序列依赖关系的噪声处理[J]. 地球物理学报, 2014, 57(2): 531-545.
WANG Hui, WEI Wenbo, JIN Sheng, et al. Removal of magnetotelluric noise based on synchronous time series relationship[J]. Chinese Journal of Geophysics, 2014, 57(2): 531-545.
[11] 吕庆田, 董树文, 汤井田, 等. 多尺度综合地球物理探测:揭示成矿系统、助力深部找矿——长江中下游深部探测(SinoProbe-03)进展[J]. 地球物理学报, 2015, 58(12): 4319-4343.
L Qingtian, DONG Shuwen, TANG Jingtian, et al. Multi-scale and integrated geophysical data revealing mineral systems and exploring for mineral deposits at depth: a synthesis from SinoProbe-03[J]. Chinese Journal of Geophysics, 2015, 58(12): 4319-4343.
Qingtian, DONG Shuwen, TANG Jingtian, et al. Multi-scale and integrated geophysical data revealing mineral systems and exploring for mineral deposits at depth: a synthesis from SinoProbe-03[J]. Chinese Journal of Geophysics, 2015, 58(12): 4319-4343.
[12] 李晋, 汤井田, 王玲, 等. 基于信号子空间增强和端点检测的大地电磁噪声压制[J]. 物理学报, 2014, 63(1): 019101.
LI Jin, TANG Jingtian, WANG Ling, et al. Noise suppression for magnetotelluric sounding data based on signal subspace enhancement and endpoint detection[J]. Acta Phys Sin, 2014, 63(1): 019101.
[13] 汤井田, 李晋, 肖晓, 等. 数学形态滤波与大地电磁噪声压制[J]. 地球物理学报, 2012, 55(5): 1784-1793.
TANG Jingtian, LI Jin, XIAO Xiao, et al. Mathematical morphology filtering an noise suppression of magnetotelluric sounding data[J]. Chinese Journal of Geophysics, 2012, 55(5): 1784-1793.
[14] 李晋, 汤井田, 肖晓, 等. 基于组合广义形态滤波的大地电磁资料处理[J]. 中南大学学报(自然科学版), 2014, 45(1): 173-185.
LI Jin, TANG Jingtian, XIAO Xiao, et al. Magnetotelluric data processing based on combined generalized morphological filter[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 173-185.
[15] 李兵, 张培林, 刘东升, 等. 基于自适应多尺度形态梯度变换的滚动轴承故障特征提取[J]. 振动与冲击, 2011, 30(10): 104-108.
LI Bing, ZHANG Peilin, LIU Dongsheng, et al. Feature extraction for roller bearing fault diagnosis based on adaptive multi-scale morphological gradient transformation[J]. Journal of Vibration and Shock, 2011, 30(10): 104-108.
[16] WANG R Q, LI Q, ZHANG M. Application of multi-scaled morphology in denoising seismic data[J]. Applied Geophysics, 2008, 5(3): 197-203.
[17] MARAGOS P. Pattern spectrum and multiscale shape representation[J]. IEEE Trans on Pattern Analysis and Machine Intelligence, 1989, 11(7): 701-716.
[18] ECKMANN J P, KAMPHORST S O, RUELLE D. Recurrence plots of dynamical systems[J]. Europhysics Letters, 1987, 4(9): 973-977.
[19] 杨栋, 任伟新, 李丹, 等. 基于局部递归率分析的振动信号非平稳评价[J]. 中南大学学报(自然科学版), 2013, 44(7): 3024-3032.
YANG Dong, REN Weixin, LI Dan, et al. Local recurrence rate analysis based non-stationarity measurement for operational vibration signal[J]. Journal of Central South University (Science and Technology), 2013, 44(7): 3024-3032.
(编辑 陈灿华)
收稿日期:2015-10-11;修回日期:2015-12-06
基金项目(Foundation item):国家自然科学基金资助项目(41404111, 41304098);国家高技术研究发展计划(863计划)资助项目(2014AA06A602);湖南省自然科学基金资助项目(2015JJ3088);中国博士后科学基金资助项目(2015M570687) (Projects(41404111, 41304098) supported by the National Natural Science Foundation of China; Project (2014AA06A602) supported by the National High Technology Research and Development Program of China; Project(2015JJ3088) supported by the Natural Science Foundation of Hunan Province; Project(2015M570687) supported by the Postdoctoral Science Foundation of China)
通信作者:汤井田,博士,教授,从事信号处理及电磁法数值模拟研究;E-mail: jttang@csu.edu.cn