将式(1)改写为如下一元方程形式:
 (2)
(2)
对g(ts)求导得:

 (3)
(3)
其中:(xs(ts), ys(ts), zs(ts))表示卫星位置;(xu(t), yu(t), zu(t))表示接收机位置;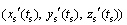 表示卫星速度。根据卫星导航系统的特点,取导航卫星速度最大为5 km/s,星地最小距离为2.5×107 m,忽略电离层、对流层变化率,则
表示卫星速度。根据卫星导航系统的特点,取导航卫星速度最大为5 km/s,星地最小距离为2.5×107 m,忽略电离层、对流层变化率,则 5×10-5<1。因此,采用定点迭代法求解伪距时,算法收敛。
5×10-5<1。因此,采用定点迭代法求解伪距时,算法收敛。
1.2 伪距动态模型参数计算
为了满足高动态条件下的伪距模拟要求,通常使用伪距的3阶泰勒展开多项式作为伪距动态模型[9-11],如式(4)所示。该模型在信号处理中采用多阶DDS累加器结构实现,由于忽略高阶项,需要周期计算伪距动态模型的各阶项系数。
 (4)
(4)
式中:a(tN)为加速度;j(tN)为加加速度。
计算伪距动态模型参数时,根据已知固定时间间隔的伪距及其变化率,常采用Hermite插值、样条插值等方法。其中分段三阶样条插值方法无需求解伪距变化率,且精度较高,是一种较理想的伪距动态模型参数计算方法[7]。同时,在工程实现中,GNU科学库已提供样条插值算法的快速计算函数[12],使用方便。
2 伪距计算优化方法
高精度GNSS信号模拟器的伪距计算方法包含从仿真数学模型计算伪距至插值算法得出动态模型参数的整个过程。为了减小运算量,并保证伪距计算的高精度,可以对伪距计算过程进行优化,提出的伪距优化方法主要包含以下3个方面的改进。
1) 使用插值算法计算卫星位置。高精度GNSS信号模拟器要求使用轨道动力学积分方法计算卫星轨道,并且伪距计算时需要多次求解任意时刻的卫星位置。若均采用动力学积分方法计算,则运算量较大。一种合理的优化方法是采用动力学积分方法计算一定时间间隔的轨道数据,然后通过插值算法计算任意时刻的卫星位置。
2) 信道延迟量不参与迭代计算。电离层延迟、对流层延迟等信道延迟量与接收机同卫星之间的夹角有关。通常高精度伪距计算时,会迭代重新计算这些延迟量。但是,伪距迭代计算前后,夹角通常变化很小。所以,可以考虑在损失一定伪距计算精度的条件下,在迭代计算过程中不计算信道延迟,以减少运算量的优化方法。
3) 不同动态条件下的伪距时间间隔。根据接收机的运动速度,可以将信号模拟器的动态特性分为静态、中低动态和高动态3种环境。通常伪距动态模型参数的更新频率固定不变,因此,为了满足高动态特性要求,需要计算时间间隔较小的伪距,以提高插值算法精度。然而,如果统一采用高动态条件下的伪距计算时间间隔,对于其他动态环境,将造成浪费。为此,针对不同动态特性选择合适的时间间隔计算伪距,是一种合理的优化方法。
3 仿真论证及性能分析
根据伪距计算优化方法提出的3个改进方式,下面通过仿真实验,论证优化算法的具体步骤及其性能。
3.1 卫星轨道插值计算
采用卫星动力学模型计算卫星轨道时,可以准确计算出卫星的位置和速度,因此选择精度较高的分段三阶Hermite插值算法作为卫星轨道的插值算法[13]。文献[13]指出当卫星轨道误差小于1 cm时,对定位结果的影响可以忽略,因此,插值算法的精度要求满足小于1 cm。
仿真时,卫星动力学积分法使用的摄动力模型如表1所示。实验方法为使用卫星动力学模型计算1 h,时间间隔5 ms的原始轨道数据。然后分别选择不同时间间隔下的轨道数据作为样本数据,并使用Hermite插值算法得到5 ms的插值数据。通过与原始轨道数据比较,得出最优时间间隔。仿真结果如图2所示。
由图2可以看出:采用分段3阶Hermite插值算法计算卫星轨道,当时间间隔取120 s时,最大位置误差为4.46 mm,最大速度误差为0.44 mm/s,伪距计算误差小于6×10-7 m。同时与动力学积分法计算相同时间长度的卫星轨道耗时比较,计算效率提高16倍。
表1 摄动力模型
Table 1 Model of forces


图2 卫星轨道插值算法仿真结果
Fig. 2 Simulation results of satellite orbits interpolation algorithm
3.2 信道延迟量影响
信道延迟量主要包括电离层延迟和对流层延迟。为了分析迭代计算伪距时,忽略信道延迟量对计算精度的影响,采用如下仿真方法。分别计算5 h时间内的传统高精度伪距计算方法和优化方法的伪距值,并作差得到优化算法的误差。其中电离层延迟使用Klobuchar模型,对流层延迟使用Hopfield模型,仿真结果如图3所示。

图3 误差项影响仿真结果
Fig. 3 Simulation results of error affecting
由图3可以看出:伪距误差随着仰角的减少逐渐增大,最大误差在3×10-5 m以内。同时,通过统计1 000次重复计算相同时刻伪距的计算时间,得出优化算法计算效率提高了约1倍。
3.3 不同动态条件下的伪距时间间隔
根据已知时间间隔的伪距,采用分段三阶样条插值算法计算伪距动态模型参数时,针对不同的动态条件,可以选择不同的伪距时间间隔。实验仿真时,分别选择静态、中低动态和高动态3种场景。其中,在中低动态条件下,接收机的运动速度为1 000 m/s。在高动态条件下,选择JPL实验室推荐的一种具有典型意义的高动态运动模型[14],该高动态环境的接收机速度的变化曲线如图4所示。

图4 高动态环境速度变化曲线
Fig. 4 Curve of high dynamic environment velocity
表2 不同动态条件下的插值算法精度
Table 2 Pseudorange accuracy under different dynamic environments

仿真时,接收机的初始位置设置为仿真开始时刻卫星星下点位置,并且接收机始终沿该时刻垂直高度方向运动。分别选择不同时间间隔条件的原始伪距数据,然后使用样条函数计算1 ms间隔的伪距值。通过与原始数据比较,得出不同时间间隔条件下的伪距动态模型参数计算精度,仿真结果如表2所示。
由表2可见:对于静态条件,选择时间间隔20 s时,伪距计算精度就可以达到2.43×10-5 m;对于中低动态时,选择时间间隔2 s时,伪距计算精度可以达到2.96×10-4 m;对于高动态条件时,时间间隔选择0.1 s时,伪距计算精度可以达到3.71×10-4 m。
4 结论
1) 根据卫星导航系统的特征及定点迭代法收敛定理,证明了伪距计算时的算法收敛性问题。
2) 为了减少伪距计算过程的运算量,提出了一种优化算法,其具体步骤为:① 使用分段三阶Herimite插值算法计算任意时刻的卫星轨道,已知卫星轨道数据的时间间隔为120 s;② 迭代计算卫星发射时刻过程时,忽略信道延迟量的影响;③ 使用三阶样条函数计算伪距动态模型参数时,对于静态条件,已知伪距时间间隔为20 s;对于中低动态条件,时间间隔为2 s;对于高动态条件,时间间隔为0.1 s。
3) 使用伪距计算优化算法时,计算误差小于1 mm(即伪距损失精度1 mm),计算效率大幅度提高。
致谢:感谢中国科学院上海天文台黄勇博士在卫星轨道积分算法方面提供的帮助。
参考文献:
[1] 赵军祥. 高动态智能GPS卫星信号模拟器软件数学模型研究[D]. 北京: 北京航空航天大学电子信息工程学院, 2003: 55-67.
ZHAO Junxiang. The study on mathematical model of high dynamic and intelligent GPS satellite signal simulator software[D]. Beijing: Beihang University. School of Electronic and Information Engineering, 2003: 55-67.
[2] 吕志成. 高动态卫星导航信号模拟器软件研究[D]. 长沙: 国防科学技术大学电子科学与工程学院, 2006:23-30.
L Zhicheng. The research of the high dynamic satellite signal simulator software[D]. Changsha: School of National University of Defense Technology. School of Electronic Science and Engineering, 2006: 23-30.
Zhicheng. The research of the high dynamic satellite signal simulator software[D]. Changsha: School of National University of Defense Technology. School of Electronic Science and Engineering, 2006: 23-30.
[3] 李成军, 陆明泉, 冯振明. GPS中频信号模拟器的数学模型及实现[J]. 清华大学学报(自然科学版), 2008, 48(10): 1582- 1585.
LI Chengjun, LU Mingquan, FENG Zhenming. Mathematical model and realization for GPS IF signal simulator[J]. Journal of Tsinghua University(Science and Technology), 2008, 48(10): 1582-1585.
[4] 罗益鸿. 导航卫星信号模拟器软件设计与实现[D]. 长沙: 国防科学技术大学机电工程与自动化学院, 2008: 29-43.
LUO Yihong. The software design and implementation of navigation satellite signal simulator[D]. Changsha: National University of Defense Technology. College of Mechatronics Engineering and Automation, 2008: 29-43.
[5] 沙海, 吕志成, 张国柱, 等. 多系统卫星导航信号模拟源的系统结构与软件设计[C]// 第二届卫星导航学术年会. 上海, 2011: 341-345.
SHA Hai, L Zhicheng, ZHANG Guozhu, et al. System architecture and software design of multi-system satellite navigation signal simulator[C]// The Second China Satellite Navigation Conference. Shanghai, 2011: 341-345.
Zhicheng, ZHANG Guozhu, et al. System architecture and software design of multi-system satellite navigation signal simulator[C]// The Second China Satellite Navigation Conference. Shanghai, 2011: 341-345.
[6] Song Y, Zhou H, Zeng T, et al. Algorithm and realization of high dynamic satellite signal doppler simulation based on FPGA[C]// Proceedings of the 2010 International Technical Meeting of Institute of Navigation. San Diego, USA, 2010: 1044-1050.
[7] 刘旻, 吴嗣亮. 实时高动态GNSS信号模拟器高精度伪距生成方法[J]. 北京理工大学学报, 2011, 31(9): 1053-1057.
LIU Min, WU Siliang. Method of high accuracy pseudorange generation for real-time high dynamic GNSS signal simulator[J]. Transactions of Beijing Institute of Technology, 2011, 31(9): 1053-1057.
[8] 丁丽娟. 数值计算方法[M]. 北京: 北京理工大学出版社, 1997: 184-187.
DING Lijuan. Numerical computation method[M]. Beijing: Beijing Institute of Technology Press, 1997: 184-187.
[9] 齐巍, 常青, 洪晟. 导航信号模拟器可见卫星同步调度算法[J]. 沈阳工业大学学报, 2011, 33(4): 428-433.
QI Wei, CHANG Qing, HONG Sheng. Algorithm for synchronous scheduling of visible satellite based on navigation signal simulator[J]. Journal of Shenyang University of Technology, 2011, 33(4): 428-433.
[10] ZHAO Yun, KOU Yanhong, HUANG Zhigang. Multi- Constellation GNSS signal simulator and its software implementation[C]// 22nd International Meeting of the Satellite Division of the Institute of Navigation. Savannah GA, 2009: 2213-2219.
[11] 宋媛媛, 曾大治, 曾涛. 基于三阶DDS的卫星信号多普勒模拟方法[J]. 北京理工大学学报, 2010, 30(10): 1213-1216.
SONG Yuanyuan, ZENG Dazhi, ZENG Tao. Satellite signal doppler simulation method based on third-order DDS[J]. Transactions of Beijing Institute of Technology, 2010, 30(10): 1213-1216.
[12] Mark Galassi. GNU scientific library[EB/OL]. [2009-08-25]. http://www.gnu.org.
[13] Korvenoja P, Piche R. Efficient satellite orbit approximation[C]// The 13th International Technical Meeting of the Satellite Division of The Institute of Navigation. Salt Lake City, USA, Sept, 2000: 1930-1937.
[14] 向洋. 高动态GPS载波跟踪技术研究[D]. 武汉: 华中科技大学电信系, 2010: 22-52.
XIANG Yang. Study on high dynamic GPS carrier tracking techniques[D]. Wuhan: Huazhong University of Science and Technology. Department of Electronic and Information Engineering, 2010: 22-52.
(编辑 杨幼平)
收稿日期:2013-10-11;修回日期:2013-12-28
基金项目(Foundation item):国家自然科学基金青年科学基金资助项目(61403413) (Project (61403413) supported by National Natural Science Youth Foundation of China)
通信作者:沙海(1984-),男,河南新乡人,博士研究生,从事卫星导航的研究;电话:13311007589;E-mail:sandhai@163.com