Experimental investigation on predicting precursory changes in entropy for dominant frequency of rockburst
来源期刊:中南大学学报(英文版)2020年第10期
论文作者:王春来 陈增 廖泽锋 侯晓琳 李海涛 王爱文 李长峰 钱鹏飞 李广永 卢辉
文章页码:2834 - 2848
Key words:rockburst; precursory information; acoustic emission; information entropy; dominant frequency; evolution model
Abstract: Rockburst is a dynamic phenomenon accompanied by acoustic emission (AE) activities. It is difficult to predict rockburst accurately. Based on the fast Fourier transform (FFT) method and the information entropy theory, the evolution model of dominant frequency entropy was established. The AE energy, frequency and stress were synthetically considered to predict rockburst. Under the triaxial and the single-face unloading tests, the relationship between AE energy and the development of internal cracks was analyzed. Using the FFT method, the distribution characteristics of AE dominant frequency values were obtained. Based on the information entropy theory, the dominant frequencies evolved patterns were ascertained. It was observed that the evolution models of the dominant frequency entropy were nearly the same and shared a characteristic “undulation-decrease-rise-sharp decrease” pattern. Results show that AE energy will be released suddenly before rockburst. The density of intermediate frequency increased prior to rockburst. The dominant frequency entropy reached a relative maximum value before rockburst, and then decreased sharply. These features could be used as a precursory information for predicting rockburst. The proposed relative maximum value could be as a key point to predict rockburst. This is a meaningful attempt on predicting rockburst.
Cite this article as: WANG Chun-lai, CHEN Zeng, LIAO Ze-feng, HOU Xiao-lin, LI Hai-tao, WANG Ai-wen, LI Chang-feng, QIAN Peng-fei, LI Guang-yong, LU Hui. Experimental investigation on predicting precursory changes in entropy for the dominant frequency of rockburst [J]. Journal of Central South University, 2020, 27(10): 2834-2848. DOI: https://doi.org/10.1007/s11771-020-4506-8.

J. Cent. South Univ. (2020) 27: 2834-2848
DOI: https://doi.org/10.1007/s11771-020-4506-8

WANG Chun-lai(王春来)1, CHEN Zeng(陈增)1, LIAO Ze-feng(廖泽锋)1, HOU Xiao-lin(侯晓琳)1,
LI Hai-tao(李海涛)2, WANG Ai-wen(王爱文)3, LI Chang-feng(李长峰)1, QIAN Peng-fei(钱鹏飞)1,
LI Guang-yong(李广永)1, LU Hui(卢辉)4
1. School of Energy and Mining Engineering, China University of Mining and Technology Beijing,Beijing 100083, China;
2. Safety Technology Branch, CCTEG China Coal Research Institute, Beijing 100013, China;
3. School of Mechanics and Engineering, Liaoning Technology University, Fuxin 123000, China;
4. Center for Underground Construction and Tunnelling, Colorado School of Mines, Golden,Colorado 80401, USA
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2020
Abstract: Rockburst is a dynamic phenomenon accompanied by acoustic emission (AE) activities. It is difficult to predict rockburst accurately. Based on the fast Fourier transform (FFT) method and the information entropy theory, the evolution model of dominant frequency entropy was established. The AE energy, frequency and stress were synthetically considered to predict rockburst. Under the triaxial and the single-face unloading tests, the relationship between AE energy and the development of internal cracks was analyzed. Using the FFT method, the distribution characteristics of AE dominant frequency values were obtained. Based on the information entropy theory, the dominant frequencies evolved patterns were ascertained. It was observed that the evolution models of the dominant frequency entropy were nearly the same and shared a characteristic “undulation-decrease-rise-sharp decrease” pattern. Results show that AE energy will be released suddenly before rockburst. The density of intermediate frequency increased prior to rockburst. The dominant frequency entropy reached a relative maximum value before rockburst, and then decreased sharply. These features could be used as a precursory information for predicting rockburst. The proposed relative maximum value could be as a key point to predict rockburst. This is a meaningful attempt on predicting rockburst.
Key words: rockburst; precursory information; acoustic emission; information entropy; dominant frequency; evolution model
Cite this article as: WANG Chun-lai, CHEN Zeng, LIAO Ze-feng, HOU Xiao-lin, LI Hai-tao, WANG Ai-wen, LI Chang-feng, QIAN Peng-fei, LI Guang-yong, LU Hui. Experimental investigation on predicting precursory changes in entropy for the dominant frequency of rockburst [J]. Journal of Central South University, 2020, 27(10): 2834-2848. DOI: https://doi.org/10.1007/s11771-020-4506-8.
1 Introduction
Shallow mineral resources are nearing exhaustion. As the depth of mining gradually deepens, it will be in high ground stress, high osmotic pressure and high temperature conditions, which could cause the occurrence of mining dynamic disasters and lead to casualties and property losses [1, 2]. Therefore, it has become a key issue for scholars and engineers to predict dynamic disasters in geotechnical engineering. Before the occurrence of mining dynamic disasters, considerable precursory information will be released [3]. An urgent problem remaining is being able to predict the time and spatial location of a disaster from such precursory information through the application of a universal regular pattern.
The dynamic evolution of the internal microfracture can be monitored continuously using acoustic emission (AE) technology for rock materials. Therefore, AE test is a widely accepted method of forecasting rock failure [4]. Being the physical responses arising from rockburst, AE activities are closely related to the property of the rockburst, and their measurement has become a highly effective method for the real-time monitoring of rockburst [5-7]. It is widely used in laboratory testing and site monitoring [8-12]. CHEON et al [13] conducted shear tests using improved AE equipment and established criteria for rockburst. WANG et al [14, 15] found that there is a relatively quiet period in AE signal activities and the value of load-unload response ratio is close to 1 before rockburst. ZHAO et al [16] through AE monitoring found that the rock sample is prone to strainburst failure under a high unloading rate.
To date, researches on rock AE phenomena were mainly focused on AE parameters. However, the drawback of the parameter analysis method was that the intrinsic information about the AE source was often overshadowed or obscured by the characteristics of the sensors [17]. Waveform analysis technology may avoid this problem because AE waveforms carry a large amount of information, including the stress state, structure, physical and mechanical properties of rock [18-20]. Hence, the analysis of AE waveforms contributes to the understanding of rockburst mechanisms and damage precursors. BENSON et al [21] found that there is a significant reduction in disordered AE signals before the rock failure. HE et al [22] presented an AE experimental strainburst study and found that there are much higher amplitude and lower frequency events near the bursting failure. Meanwhile, the strainburst tests on sandstone showed a result of the influence of anisotropic structures on rock failure responses [23]. LU et al [24, 25] demonstrated that the dominant frequency of the main shock signal and the rockburst intensity were negatively correlated. The aforementioned results from abundant experimental studies have shown that it is indeed to possible to explore the intrinsic information of an AE source by using the spectrum analysis method. However, how this information could be specifically utilized to predict rockburst occurrence has not been substantially investigated.
To study the distribution characteristics of dominant frequencies, the concept of information entropy was introduced. As a measure of the dispersion and complexity of a system, entropy has been widely applied in seismology, nonlinear dynamics systems, physics and rock mechanics. LOVALLO et al [26] suggested that information entropy could be related to earthquake magnitude and that aftershocks cause the increase in information entropy and the decrease in disequilibrium and complexity in a seismic sequence. MAIN et al [27] derived an analytical expression for entropy production in earthquake populations and found that the maximum entropy production solution exhibits the universally observed Gutenberg-Richter b value of approximately 1 in frequency-magnitude data. Based on information theory, PALUS et al [28, 29] presented a multivariate version of the method for testing the nonlinear activities of meteorology and physiology and found that uncertainty increases over in time due to the positive information production rate. CHAI et al [17] proposed a new qualitative parameter to discriminate the different damage stages and identify the critical damage with AE entropy based on Shannon’s entropy. The characteristics of the seepage system in a complex rock mass dam were analyzed by CHEN et al [30] based on the entropy theory. An equation for the vertical distribution of the seepage velocity in a dam borehole was derived, and the results were well in accordance with actual field data. Rockburst is a nonlinear dynamic process that changes from chaos to an ordered state. Therefore, the information entropy can be used in rock mass engineering.
In this study, we performed the laboratory rockburst tests on granite specimens and obtained AE signals throughout the entire process of rockburst. Then, we calculated the dominant frequency values by FFT spectrum analysis method and studied its distribution characteristics during the rockburst. To study the distribution characteristics of the dominant frequency, based on the information entropy theory, we analyzed the evolution pattern of the dominant frequency from chaos to an ordered state before the rockburst. The predicting key points were identified and the evolution model was established based on the dominant frequency entropy. Thus, this approach provides a meaningful discovery for predicting rockburst.
2 Experiment and methods
2.1 Experimental equipment
The experimental equipment includes a VEGA scanning electron microscope (SEM), an energy dispersive spectrometer (EDS) with the relevant INCA analysis software (Oxford Instruments Co., Tokyo, Japan), the load control system of the computer controlled electro-hydraulic servo rock triaxial testing machine (WAW-600), and the AE testing system (PCI-2 fully digital AE signal collection). Testing data of granite samples can be precisely and automatically obtained using the WAW-600. The AE testing system consists of the AE data processing system, AE sensors, preamplifiers, host computer and Windows-based AE software. This system is a fully digital, multi-channel system with PCI-2 board card that minimizes sampling noise. Meanwhile, all AE parameters can be obtained by the AE testing system. The curves of AE parameters are depicted automatically on the AEwin software platform. The laboratory data were processed and analyzed in Excel, obtaining rock mechanics parameters and depicting the curves.
2.2 Sample preparation
In the experiment, granite samples were collected from a quarry in Lingshou County, China. The main geological structure of the quarry is the SW-NE synclinal fold. There are many strike and incline faults, contact fracture zones and secondary tectonic features. All granite specimens were taken from the same rock mass. The rock has a dense texture and a gray-white color with white veins. It has a strong strain energy storage capacity and a stronger rockburst tendency [31].
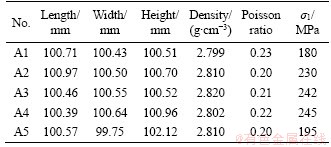
All samples were processed into cubes with a length of 100 mm. The flatness of 6 surfaces was less than 0.02 mm, and the parallelism between the top and bottom surface was less than 0.05 mm. The physio-mechanical properties of the granite specimens are shown in Table 1.
Table 1 Physico-mechanical properties of granite samples
2.3 Experimental design and methods
In the experiment, the triaxial testing machine and AE testing system were synchronously operated to monitor the mechanical behaviours and AE characteristics of the specimens in real time. Based on previous research [22, 23, 32, 33], the loading path was designed as follows:
1) The sample was pressured to a certain value to simulate the original rock stress. According to the field stress test, we simplified it and determined that the original rock stress state was  15 MPa,
15 MPa,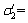
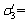 10 MPa. In order to make that the simulated stress in the three directions reaches the original state at the same time, the loading speed was V1=0.03 MPa/s,V2=0.02 MPa/s.
10 MPa. In order to make that the simulated stress in the three directions reaches the original state at the same time, the loading speed was V1=0.03 MPa/s,V2=0.02 MPa/s.
2) Keep the pressure constant for 5 min, and then, a single-face of the direction 3 was suddenly unloaded, resulting into the single-face being exposed as a free surface.
3) Keep the stress constant; use displacement control to simulate the in-situ state so that to keep the sample stable for the loading surface of direction; increase the pressure to destroy the sample. The loading speed was V1=0.2 MPa/s. The loading path is shown in Figure 1.
For the AE monitoring system, 6 AE sensors were used to detect the signals in the experiment. The resonant frequency of the sensor was 20-400 kHz, the sampling frequency setting was 1 MHz, and the preamplifier parameters were set to 40 dB. Before the experiment, we tested the background noise, and the result showed that the background noise is around 45 dB. Therefore, the threshold value was set at 45 dB to minimize the influence of background noise. To better receive AE signals, the sensors surfaces were coated with petroleum jelly. Meanwhile, the sensors were fixed by plasticine. The arrangement of AE sensors is shown in Figure 2. Before the experiment, we conducted the lead-off test to confirm that each channel could receive the AE signal steadily. Meanwhile, SEM and EDS analysis tests were conducted to obtain the surface characteristic, spatial distribution pattern, and chemical composition on samples.
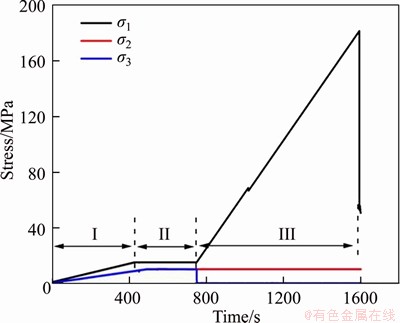
Figure 1 Loading path of samples
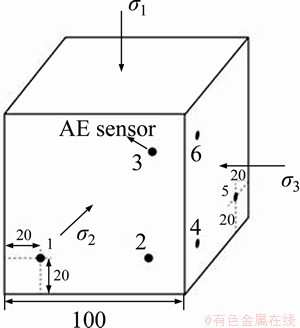
Figure 2 Arrangement of AE sensors (Unit: mm)
3 Theoretical basis and calculation
3.1 FFT
Proposed by COOLEY et al [34], the FFT is a fast computation method for the discrete Fourier transform (DFT), which is an improved form of the DFT based on the odd, even, imaginary, real and other characteristics. The FFT does not provide any findings different from the DFT, but it substantially improves the arithmetic speed and efficiency of the DFT. The FFT formula is as follows:
 (1)
(1)
where X(j) is the input sequence; N is the frequency points; WN is the twiddle factor and is defined as
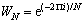 (2)
(2)
For ascertaining the discreteness of AE signal waveforms, FFT analysis has been widely used as a kind of spectral analysis method, as it can well reflect the global spectrum characteristics of the waveforms. In this study, the AE signal waveforms generated during the process of rockburst were processed using software; FFT analysis was performed for the waveforms. Two-dimensional spectra could be obtained. The frequency corresponding to the maximal amplitude value in the two-dimensional spectrum was defined as the dominant frequency. The detailed procedure is as follows:
1) Obtain all original AE waveforms using software (Figure 3(a)). Figure 3(a) shows one original AE waveforms at 2 s.
2) Process the original waveforms using the FFT spectrum analysis method to obtain the spectrum (Figure 3(b)). Figure 3(b) shows the spectrum obtained by analyzing the original waveforms at 2 s for sample A1. Then we could calculate that the dominant frequency value as 103375 Hz.
3) Calculate all dominant frequencies during the rockburst process. All the dominant frequencies would be shown in Section 4.3.
3.2 Information entropy theory
Entropy is a concept from thermodynamics, which could be adopted as a measure of disorder: the entropy increases as the system becomes more chaotic. To measure uncertainty, SHANNON [35] first systematically put forth a concept of information measurement. Based on the methods of probability and statistics, he calculated the uncertainty of a random event with entropy and solved the problem of quantitative measurement of information. For a probability test with N results, set the results with discrete probability λ each. Meanwhile, if
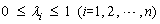 (3)
(3)
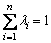 (4)
(4)
then
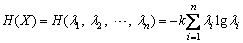 (5)
(5)
where H is the information entropy, also called probability entropy or Shannon entropy; k is a constant and k≥0.
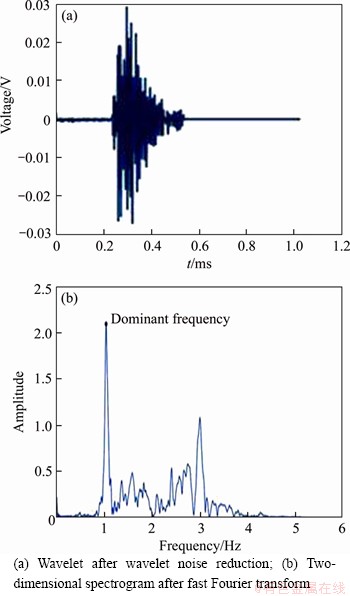
Figure 3 Original signal and the spectrum for A1 at 2 s:
The deformation and failure of the rock mass is a nonlinear dynamic process change from chaos to an ordered state. Thus, the information entropy could be applied in rock engineering. In this study, all dominant frequency values in the Ⅲ stage of loading were calculated for the entropy values using Matlab software. The supposed dominant frequency is x(n), and n=1-N, is the quantity of AE signal waveforms. The detailed process is as follows:
1) Find and group the distribution range of x(n).
2) Obtain the counts of each group of dominant frequency in unit time interval and calculate the corresponding probability.
3) Solve the entropy values with the information entropy formula.
4 Experimental results and analysis
4.1 SEM-EDS experiment
Granites often form well-developed, macroscopically identifiable mineral particles of different sizes. We can observe the surface morphology of the sample and analyze the chemical composition in the micro zone through SEM and EDS analysis. Figure 4 shows SEM images of a granite sample at magnifications of 200 times, 500 times and 2000 times. The secondary electron image (SEI) clearly shows the topography of the granite surface. The backscattered component image (COMPO) can observe the contrast image formed by the component difference in the area, which can assist component analysis. Figure 5 depicts the energy dispersion spectrum. According to the COMPO, two representative positions of the sample are selected and the element composition is analyzed. Tables 2 and 3 show the chemical composition of the granite samples at different locations. 200 times and 500 times SEM figures show that the granite specimen cross section is composed of rugged grains. The size of the crystal is between 30 and 80 μm. The intergranular cementation is good. There are obvious weak surface and bright filling between the crystal particles. 2000 times SEM figures show different types of particles inlaid with each other, and the rock heterogeneity is strong. Bright filling particles are loosely distributed, and the intergranular weak surface is large, which plays a significant role in the formation and development of granite cracks. EDS analysis shows that the main component of granite is SiO2, and the composition is relatively simple (Figure 5(c)-(d) and Table 3). The bright filling between particles is mainly iron, which is well articulated (Figures 5(a)-(b) and Table 2). It is also the reason for the high strength of granite. SEM results show the characteristics of heterogeneity and porous in rock material, such as the existence of micro-cracks, micro-cavities and minerals of differing hardness. When rock samples are loaded, the material heterogeneity leads to the propagation of micro-cracks, which could be observed by AE monitoring.

Figure 4 SEM image at magnification of granite sample:
4.2 Rock mechanical characteristics and AE parameters
In this paper, information entropy was calculated in time series. Therefore, we described the mechanical properties of rock samples using time-stress curves. Figure 6 shows the relationship between AE parameters and time-stress curves for the granite samples. The AE parameters included two important parameters, accumulated AE energy and AE energy rate. AE energy value is equal to the area enclosed by the signal envelope and the time axis. It can reflect the relative energy and strength of AE events. AE energy rate is defined as the released energy of samples AE signals per unit time and is an essential parameter of the evolution of the AE energy. It can reflect the effects of time and energy simultaneously. From Figure 6, the peak strength and AE characteristic were observed differently, which verify the anisotropy of the rock mass. Meanwhile, the anisotropy of the rock mass leads to different rock mechanics and AE characteristics. The curve of time-stress had no obvious nonlinear phase before and after yield, which is typical of brittle failure. In practical engineering, the greater the brittleness of the rock mass is, the easier it is to store more elastic energy, which will lead to a stronger rockburst. In addition, as shown in Figure 6, in the process of loading to the original rock stress (i.e., the I stage of loading),there was very little AE energy, and the curve almost parallels to the x-axis, indicating that the internal micro-cracks and holes in the rock were extremely undeveloped and dormant. In the process of constant pressure (i.e., the II stage of loading), the AE energy was not constant and still produced a small amount of AE energy. When loading pressure was greater than the original rock stress (i.e., the III stage of loading), the accumulated AE energy of samples A2, A3, A4 could be divided into three phases before the peak strength, namely AB, BC, phase after C. In the AB phase, the AE energy curve was approximately horizontal, with a few AE energy released. It indicated that the internal cavity and original fracture was still dormant, but there would be some slippage between the grains, resulting in a small amount of AE energy. In the BC phase, the AE energy began to be released in a large amount. As shown in Figure 6, the curve of AE energy was lifted upward with a certain slope. It indicated that there were crack initiation and local crack penetration in the samples in this phase. We could simultaneously hear sporadic sounds in the experiment. In the phase after C, the AE energy was released rapidly, and the curve of AE energy increased sharply. At this time, the samples collapsed completely, forming macro-cracks. The sample was simultaneously slabbing, showing large particle ejection phenomenon, and accompanied by a huge sound. This type of failure in the granite was commonly described as rockburst [36]. For samples A1 and A5, their AE energy curves were different from that of samples A2, A3 and A4. There was no AB phase with a few AE energy released, but there were two phases of large and sharp release of AE energy-BC and phase after C, which might be because the internal microcracks in the sample A1, A5 were activated under relatively small pressures, and began to crack initiation and penetration. This phenomenon could simultaneously verify that the axial peak strength of specimens A1 and A5 were smaller than those of specimens A2, A3 and A4. From Figure 6, the peak strengths of samples A1, A5 were less than 200 MPa, while the samples A2, A3, A4 were greater than 200 MPa. For all samples, after point C, a large amount of AE energy was generated, and the AE energy curve increases sharply, forming macroscopic macro-cracks with a rock burst phenomenon. Therefore, the point C could be viewed as the feature point, for predicting rockburst [14].
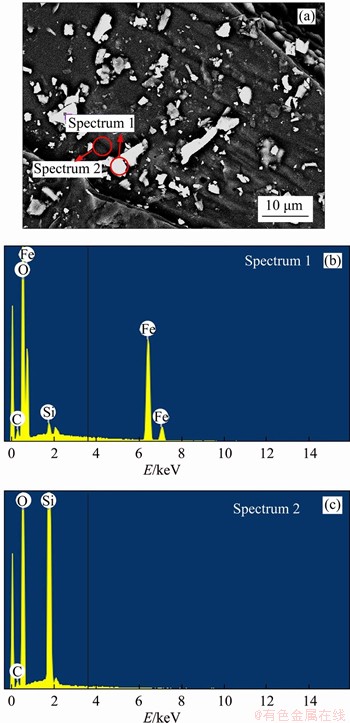
Figure 5 SEM (a) and EDS (b, c) of granite specimens
Table 2 Chemical component of spectrum 1

Table 3 Chemical component of spectrum 2
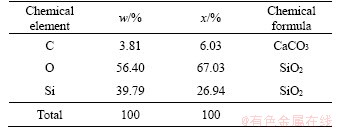
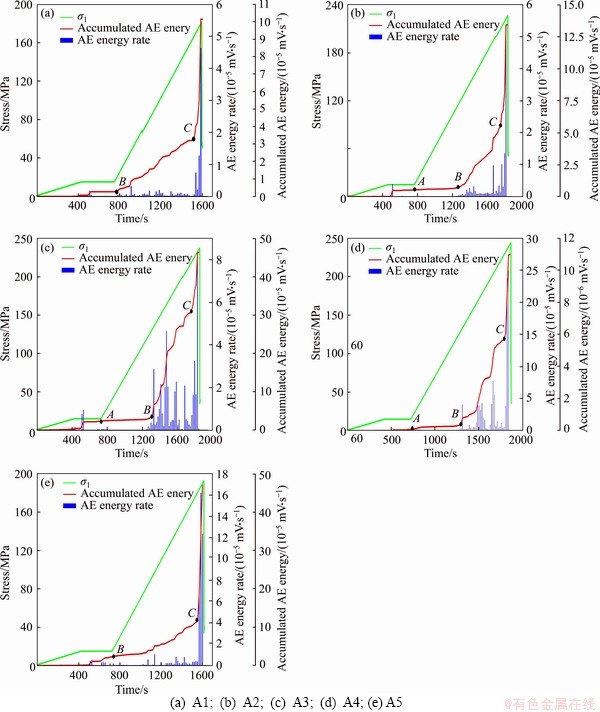
Figure 6 Relationship between time-stress curves and AE parameters for granite samples:
4.3 AE dominant frequency
AE waveforms obtained during the experiment were analyzed by FFT, and then the dominant frequencies were calculated. As shown in Figure 7, the relationship between dominant frequencies and time-stress curves was revealed.
As shown in Figure 7, the dominant frequency could be divided into three frequency bands. In this experiment, 100-175 kHz was defined as low frequency band, 175-250 kHz was defined as the intermediate frequency band, and more than 250 kHz was defined as the high frequency band. The samples had the following several characteristics:
1) High frequency AE signals were produced throughout the rock burst testing.
2) The low frequency signals were less in the initial loading period and tended to increase before the rock burst.
3) In the early stage of loading, the intermediate frequency signals density was relatively low. However, the intermediate frequency signals gradually increased as the load and deformation increased. As shown in the curve of AE energy, the area where the intermediate frequency signals were increased was exactly the phase where a large amount of the AE energy was released.
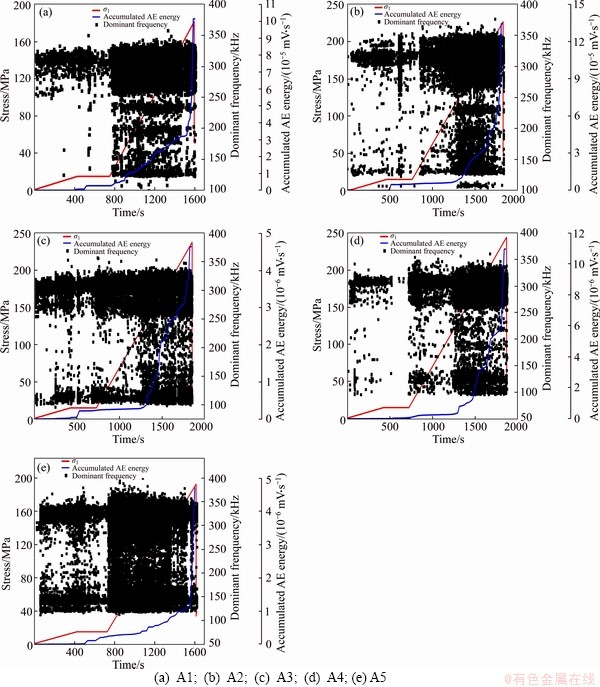
Figure 7 Relationship between time-stress curves and dominant frequencies for granite samples:
4) During the whole process of rockburst, the high and low frequency signals occurred simultaneously.
CAI et al [37] pointed out that the high- frequency band of AE was detected when small- scale low energy cracks occurred, whereas the low-frequency band was detected when large-scale high energy cracks occurred. Therefore, the change in the frequency bands could be used to indicate the state of micro-crack initiation, propagation and linking during the rockburst. Similar characteristics in the dominant frequency distributions were observed in all samples. The frequencies of each sample simultaneously also had their own individual distribution characteristics, which mainly indicated the anisotropy of the rock mass using the bandwidth and density.
As shown in Figure 7, the dominant frequency distribution was related to stress levels in the whole process of rockburst. In this study, samples A1 and A2 were taken as examples to analyze the relationship between stress and frequency distribution characteristics. In the I, II stages of loading, more high frequency signals were produced relative to the low frequency signals. The small energy source may be caused by the frictional slip of the partial mineral crystals in the original joint fissure under the condition of less pressure. The sample A1 produced less low-frequency signals, simultaneously indicating that A1 had fewer high energy sources. When it came to the III stage of loading, the distribution characteristics of intermediate frequency were obviously different between samples A1 and A2. The intermediate frequency density of sample A1 was always at a high level. As for the sample A2, the intermediate frequency density was still relatively low before 1250 s. As the pressure increased, the frequency density increased. However, the intermediate frequency of samples A1 and A2 had a common characteristic: the increase in their density and AE energy was almost synchronous (Figure 7). Rock failure is a process of crack initiation, propagation and penetration. If the high frequency signals correspond to the small crack initiation and low- frequency signals correspond to the formation of large-scale cracks, then the intermediate signal may represent the penetration between the cracks. Because of the unstable propagation of cracks, AE rupture source began to become more complex. The sample changed from a single rupture source to a variety of rupture sources, which resulted in different fracture source characteristics.
4.4 AE dominant frequency entropy
In this study, the dominant frequency entropy of the III stage of loading was calculated by software based on the information entropy theory and its calculation method. As shown in Figure 8, the relationships between the dominant frequency entropy values and time-stress curves of 5 granite samples was revealed. The following common characteristics were summarized based on the results of the 5 samples.
1) The dominant frequency entropy value varies between 0 and 1.
2) All of the curves are in fluctuation. The entropy curves show the evolution time and the value.
In this experiment, sample A2 was taken as an example. As shown in Figure 8(b), the entropy curve of sample A2 was fluctuating from 775 s to 1150 s. It is possible that the original holes and crystals were closed and slipped to produce disordered AE signals at a relatively low pressure level. The cracks were generated in an orderly manner as the pressure increased. Therefore, the entropy curve showed a decreasing trend from 1150 to 1662 s. Then, there was a slight rise between 1662 and 1716 s, potentially due to the micro-fracture formation, which resulted in a continuous generation of disordered AE signals. From 1716 to 1786 s, the entropy curve dropped sharply. The main reason may be that the development of a large number of cracks in an orderly manner eventually led to macro-cracks. In summary, the evolution pattern of sample A2 was “undulation-decline- small rise-sharp decrease”.
This entropy evolution model illustrates that rockburst is a nonlinear process in which multiple micro-cracks are initiated and propagated into macro-cracks. The initiation of micro-cracks would cause the sample to develop in a disordered direction, and the merging of micro-cracks would cause the sample to develop in an orderly direction. It manifested as the main frequency entropy would increase and then decrease. It could be concluded that at undulation stage, the initiation, propagation and merging of micro-cracks would not exist alone. As the experimental progresses, these three situations would occur simultaneously. As shown in Figure 8, the other samples shared the common entropy evolution pattern—“undulation-decline- small rise-sharp decrease”. Meanwhile, in comparison with Figure 6 and Figure 8, we found that the decrease in entropy and the increase in AE energy were almost synchronous in samples A2, A3, and A4, while they were not apparent synchronization for samples A1 and A5. It was possible that the compressive strengths of samples A1 and A5 were relatively low, cracks initiation was still disordered and the cracks did not develop in an orderly manner.
5 Discussion
5.1 Mechanical characteristics and AE parameters
In the III stage of loading, AE energy could be basically divided into three phases. From the perspective of macroscopic energy transformation,the external energy was mainly transformed into elastic strain energy and stored in the initial loading stage, during which less energy was dissipated by the radiated acoustic, electrical and magnetic signals to the surrounding environment. Therefore, in this stage, AE activities were few and their intensity was low. With the increase of external energy input, the energy was released primarily by crack initiation and penetration, and the rock radiated strong acoustic, electrical and magnetic signals. The quantity of AE activities and their intensity were consequently greatly increased. In the final phase, with the continuous input of energy, it exceeded the maximum value of the rock specimen bearing. At the same time, the elastic strain energy stored in the first two phases began to release, which results in the phenomenon of rockburst, and large energy released. From the point of microscopic crack evolution, the micro-crack initiated, propagated and nucleated before the rock peak stress, which was the fundamental reason for the macro-mechanical behavior [38]. In the first phase, the original cracks were compacted, the intensity and frequency of micro-crack initiation and propagation were low. Thereby, the rock mechanical properties were strengthened, and fewer AE energy was released. When the rock samples entered the second and third phases, micro-crack propagation accelerated, and macroscopic cracks gradually formed. The rock mechanical properties of the samples were weakened, deformation increased, and numerous AE energy were released.
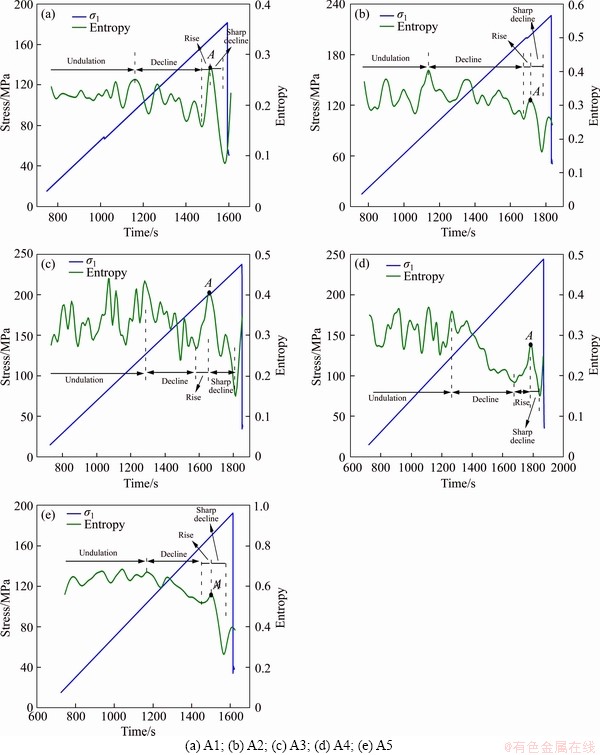
Figure 8 Relationship between time-stress curve and entropy for granite samples:
5.2 AE dominant frequency and entropy
Based on all original AE signal data and the FFT spectrum analysis method, we calculated the dominant frequency values and analyzed their distribution characteristics during rock deformation and failure. It was found that the high and low frequency bands were areas where the dominant frequencies were concentrated at the beginning of the load. Then, as the pressure increased, in the unstable crack propagation stage, the dominant frequencies were found in the broadband range. The rock samples evolved from a single rupture source to a variety of rupture sources. Previous studies have been conducted on frequency evolution. LU et al [25] performed the experiments in both the laboratory and in situ, discovering that before rockburst, precursory information (AE/MS signals) showed a tendency for the spectrum to concentrate on the low-frequency band. The spectrum of the aftershock signals moved to the high-frequency band. Moreover, a negative relationship was found between rockburst failure strength and the predominant frequency of main shock signals. BAKKER et al [39] performed a triaxial compression AE experiment and found that low-frequency signals were caused by the movement of the viscous fluid through cracks. Most prior studies focused on the qualitative analysis of frequency distribution characteristics. Few studies have investigated the evolutionary models and the possibility of rockburst occurrence with this information. Based on the information entropy theory, we investigated the evolution of dominant frequency during the deformation and failure of rock samples. Information entropy evolutionary models of 5 samples were further investigated. It should be noticed that the entropy evolution of 5 samples followed the similar pattern of “undulation-decline-rise-sharp decrease”. There was a phenomenon in which the information entropy dropped sharply can be visually observed before the failure. Before it occurred, the entropy reached a relative maximum value, A (Figure 8). The point A appeared near the peak strength. Then, the information entropy value decreased sharply. It was found that the change occurred synchronously with micro-crack merger and macro-crack formation. The entropy value variation, as far as the author is concerned, could be explained by the dissipative structure theory. When the external environment reaches a certain condition, the system will undergo mutation, which was a nonequilibrium phase transition from chaos to an ordered state of space, time or function. In this study, no macroscopic irreversible process was found inside the system during the stage of loading, which could be considered a balanced state. The information entropy presented fluctuations. With the increase of loading time, the cracks grew steadily. The cracks simultaneously stopped developing when the stress remained constant. After a period of time, a macro state that does not change with time could be found in the system, which was nearly an equilibrium state. The entropy variation tendency was still undulation. The cracks still developed in the unstable stage of crack propagation, even though the stress remains constant. The entropy values tended to decrease since the micro-rupture development was a spontaneous dynamic process. When the system absorbed energy from the outside, the system also released energy due to the fracture development. On the one hand, the macroscopic state of the system changed with time. On other hand, the distribution of micro-cracks in space was localized. This is a phase transition of the system from the disorder to ordered state when the entropy sharply decreased. The dissipative structure was formed. Due to the continuous increase in stress, after the stress reached point A, the dominant frequencies of AE signals changed from chaos to an ordered state. Therefore, there was a sharp decrease in the entropy value. Then, cracks merged rapidly, and gradually formed macro-cracks.
The sharp decrease in entropy value may provide precursory information for rockburst prediction. Therefore, point A was adopted as a predicting point for rockburst. However, a shortcoming of this study was the lack of on-site testing.
6 Conclusions
In this paper, we performed laboratory rockburst experiments with 5 granite specimens and obtained AE signals and parameters during the entire process of rock failure. The following conclusions can be made based on the experimental results:
1) The AE energy could be divided into three phases before the peak strength. The AE energy rate would suddenly increase before the rockburst, and the cumulative AE energy curve would rise almost vertically.
2) The distribution of dominant frequencies was concentrated on both high and low frequency bands at the beginning of the loading. Then, the dominant frequencies entered the broadband range before rockburst. The rock simultaneously changed from a single rupture source to a variety of rupture sources.
3) The dominant frequency entropy evolutionary models of 5 samples share a similar pattern of “undulation-decrease-rise-sharp decrease”. The dominant frequency entropy reached a relative maximum value before rockburst, and then decreased sharply, which could be selected as a precursor of rockburst. The relative maximum point of entropy was defined as the key prediction point of rockburst.
4) The sharply decreased dominant frequency entropy was proposed as a dissipative structure far from equilibrium in rock failure, an interesting result of micro-cracks propagation from chaos to ordered state.
Contributors
WANG Chun-lai contributed to the design of the study, conducted the experiments, wrote and revised the manuscript. CHEN Zeng wrote the manuscript. LIAO Ze-feng, HOU Xiao-lin and LI Chang-feng conducted experiments and data analysis. LI Hai-tao, WANG Ai-wen, QIAN Peng-fei modified the diagrams. LI Guang-yong and LU Hui edited the draft of manuscript.
Conflict of interest
WANG Chun-lai, CHEN Zeng, LIAO Ze-feng, HOU Xiao-lin, LI Hai-tao, WANG Ai-wen, LI Chang-feng, QIAN Peng-fei, LI Guang-yong, and LU Hui declare that they have no conflict of interest.
References
[1] LI Tie, CAI Mei-feng, CAI M. A review of mining-induced seismicity in China [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(8): 1149-1171. DOI: 10.1016/j.ijrmms.2007.06.002.
[2] GONG Feng-qiang, SI Xue-feng, LI Xi-bing. Experimental investigation of strain rockburst in circular caverns under deep three-dimensional high-stress conditions [J]. Rock Mechanics and Rock Engineering, 2019, 52: 1459-1474. DOI: 10.1007/s00603-018-1660-5.
[3] XU Nu-wen, TANG Chun-an, LI Hong, DAI Feng, MA Ke, SHAO Jing-dong, WU Ji-chang. Excavation-induced microseismicity: Microseismic monitoring and numerical simulation [J]. Journal of Zhejiang University-Science A, 2012, 13(6): 445-460. DOI:10.1631/jzus.a1100131.
[4] HARDY H R. Application of acoustic emission techniques to rock mechanics research [J]. Acoustic Emission, ASTM International, 1972, 41: 41-43. DOI:10.1520/stp35381s.
[5] EBERHARDT E, STEAD D, STIMPSON B, READ R S. Changes in acoustic event properties with progressive fracture damage [J]. International Journal of Rock Mechanics and Mining Sciences, 1997, 34: 3-4. DOI: 10.1016/s1365- 1609(97)00062-2.
[6] MLAKAR V, HASSANI F P, MOMAYEZ M. Crack development and acoustic emission in potash rock [J]. International Journal of Rock Mechanics and Mining Sciences, 1993, 30(3): 305-319. DOI: 10.1016/0148- 9062(94)92418-x.
[7] HE Man-cao, MIAO Jin-li, FENG Ji-li. Rock burst process of limestone and its acoustic emission characteristics under true-triaxial unloading conditions [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(2): 286-298. DOI: 10.1016/j.ijrmms.2009.09.003.
[8] EBERHARDT E, STEAD D, STIMPSO B. Quantifying progressive pre-peak brittle fracture damage in rock during uniaxial compression [J]. International Journal of Rock Mechanics and Mining Sciences, 1999, 36(3): 361-380. DOI: 10.1016/s0148-9062(99)00019-4.
[9] MORADIAN Z A, BALLIVY G, RIVARD P, GRAVEL C, ROUSSEAU B. Evaluating damage during shear tests of rock joints using acoustic emissions [J]. International Journal of Rock Mechanics and Mining Sciences, 2010, 47(4): 590-598. DOI:10.1016/j.ijrmms.2010.01.004.
[10] LU Cai-ping, DOU Lin-ming, LIU Biao, XIE Yao-she, LIU Hai-shun. Microseismic low-frequency precursor effect of bursting failure of coal and rock [J]. Journal of Applied Geophysics, 2012, 79: 55-63. DOI: 10.1016/j.jappgeo. 2011.12.013.
[11] EBERHARDT E, STEAD D, STIMPSON B, READ R S. Identifying crack initiation and propagation thresholds in brittle rock [J]. Canadian Geotechnical Journal, 1998, 35(2): 222-233. DOI:10.1139/cgj-35-2-222.
[12] ANZANI A, BINDA L, CARPINTERI G, CARPINTER A, LACIDOGNA G, MANUELLO A. Evaluation of the repair on multiple leaf stone masonry by acoustic emission [J]. Materials and Structures, 2008, 41(6): 1169-1189. DOI: 10.1617/s11527-007-9316-z.
[13] CHEON D S, JUNG Y B, PARK E S, SONG, W K, JANG H L. Evaluation of damage level for rock slopes using acoustic emission technique with waveguides [J]. Engineering Geology, 2011, 121(1): 75-88. DOI: 10.1016/j.enggeo.2011. 04.015.
[14] WANG Chun-lai. Identification of early-warning key point for rockmass instability using acoustic emission/ microseismic activity monitoring [J]. International Journal of Rock Mechanics and Mining Sciences, 2014, 71: 171-175. DOI: 10.1016/j.ijrmms.2014.06.009.
[15] WANG Chun-lai, HOU Xiao-lin, LIAO Ze-feng, CHEN Zeng, LU Zhi-jiang. Experimental investigation of predicting coal failure using acoustic emission energy and load-unload response ratio theory [J]. Journal of Applied Geophysics, 2019, 161(2): 76-83. DOI:10.1016/j.jappgeo.2018.12.010.
[16] ZHAO X G, WANG J, CAI M, CHENG C, MA L K, SU R, ZHAO F, LI D J. Influence of unloading rate on the strainburst characteristics of Beishan granite under true-triaxial unloading conditions [J]. Rock Mechanics and Rock Engineering, 2014, 47(2): 467-483. DOI: 10.1007/ s00603-013-0443-2.
[17] CHAI Meng-yu, ZHANG Zao-xiao, DUAN Quan. A new qualitative acoustic emission parameter based on Shannon’s entropy for damage monitoring [J]. Mechanical Systems and Signal Processing, 2018, 100: 617-629. DOI: 10.1016/ j.ymssp.2017.08.007.
[18] STEPHENS R W, POLLOCK A. Waveforms and frequency spectra of acoustic emissions [J]. Journal of The Acoustical Society of America, 1971, 50(3B): 904-910. DOI: 10.1121/ 1.1912715.
[19] IABBACCHIONE A T, PROSSER L J, GRAU R, OYLER D C, DOLINAR D R. Roof monitoring helps prevent injuries in stone mines [J]. Mining Engineering, 2000, 52: 32-37.
[20] ZHOU Zi-long, CHENG Rui-shan, CHEN Lian-jun, ZHOU Jing, CAI Xin. An improved joint method for onset picking of acoustic emission signals with noise [J]. Journal of Central South University, 2019, 26(10): 2878-2890. DOI: 10.1007/ s11771-019-4221-5.
[21] BENSON P M, VINCIGUERRA S, MEREDITH P G, YOUNG R P. Spatio-temporal evolution of volcano seismicity; A laboratory study [J]. Earth and Planetary Science Letters, 2010, 297(1): 315-323. DOI: 10.1016/ j.epsl.2010.06.033.
[22] HE Man-chao, MIAO Jin-li, LI De-jian, WANG Chun-guang. Experimental study on rockburst processes of granite specimen at great depth [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26: 865-876. DOI: 10.1080/10426914.2011.593231.
[23] HE Man-chao, NIE W, ZHAO Zhi-ye, GUO Wei-hua. Experimental investigation of bedding plane orientation on the rockburst behavior of sandstone [J]. Rock Mechanics and Rock Engineering, 2012, 45(3): 311-326. DOI: 10.1007/ s00603-011-0213-y.
[24] LU Cai-ping, DOU Lin-ming, LIU Hui, LIU Hai-shun, LIU Biao, DU Bin-bin. Case study on microseismic effect of coal and gas outburst process [J]. International Journal of Rock Mechanics and Mining Sciences, 2012, 53: 101-110. DOI: 10.1016/j.ijrmms.2012.05.009.
[25] LU Cai-ping, DOU Lin-ming, ZHANG nong, XUE Jun-hua, WANG Xiao-nan, LIU Hui, ZHANG Jun-wei. Microseismic frequency-spectrum evolutionary rule of rockburst triggered by roof fall [J]. International Journal of Rock Mechanics and Mining Sciences, 2013, 64: 6-16. DOI: 10.1016/j.ijrmms. 2013.08.022.
[26] LOVALLO M, LAPENNA V, TELESCA L. Transition matrix analysis of earthquake magnitude sequences [J]. Chaos, Solitons & Fractals, 2005, 24(1): 33-43. DOI: 10.1016/j.chaos.2004.07.024.
[27] MAIN I G, NAYLOR M. Entropy production and self-organized (sub) criticality in earthquake dynamics [J]. Philosophical Transactions of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, 2010, 368: 131-144. DOI:10.1098/rsta.2009.0206.
[28] PALUS M. Detecting nonlinearity in multivariate time series [J]. Physics Letters A, 1996, 213(3): 138-147. DOI: 10.1016/0375-9601(96)00116-8.
[29] PALUS M, ALBRECHT V, DVORAK I. Information theoretic test for nonlinearity in time series [J]. Physics Letters A, 1993, 175(3, 4): 203-209. DOI: 10.1016/0375- 9601(93)90827-m.
[30] CHEN Xi-xi, CHEN Jian-sheng, WANG Tao, ZHOU Huai-dong, LIU Ling-hua. Characterization of seepage velocity beneath a complex rock mass dam based on entropy theory [J]. Entropy, 2016, 18(8): 293-305. DOI: 10.3390/e18080293.
[31] GONG Feng-qiang, YAN Jing-yi, LI Xi-bing, LUO Song. A peak-strength strain energy storage index for rock burst proneness of rock materials [J]. International Journal of Rock Mechanics and Mining Sciences, 2019, 117: 76-89. DOI: 10.1016/j.ijrmms.2019.03.020.
[32] SI Xue-feng, GONG Feng-qiang. Strength-weakening effect and shear-tension failure mode transformation mechanism of rockburst for fine-grained granite under triaxial unloading compression [J]. International Journal of Rock Mechanics and Mining Science, 2020, 131: 104347. DOI: 10.1016/ j.ijrmms.2020.104347.
[33] LI Xi-bing, DU Kun, LI Di-yuan. True triaxial strength and failure modes of cubic rock specimens with unloading the minor principal stress [J]. Rock Mechanics and Rock Engineering, 2015, 48(6): 2185-2196. DOI: 10.1007/ s00603-014-0701-y.
[34] COOLEY J W, TUKEY J W. An algorithm for the machine calculation of complex Fourier series [J]. Mathematics of Computation, 1965, 19(90): 297-301. DOI: 10.1007/978-1- 4612-0667-5_9.
[35] SHANNON C E. A Mathematical theory of communication [J]. Bell System Technical Journal, 1948, 27(3): 379-423. DOI: 10.4135/9781412959384.n229.
[36] DU Kun, TAO Ming, LI Xi-bing, ZHOU Ji-an. Experimental study of slabbing and rockburst induced by true-triaxial unloading and local dynamic disturbance [J]. Rock Mechanics and Rock Engineering, 2016, 49(9): 3437-3453. DOI: 10.1007/s00603-016-0990-4.
[37] CAI M, KAISER P K, MORIOKA H, MINAMI M, MAEJIMA H, TASAKA Y, KUROSE H. FLAC/PFC coupled numerical simulation of AE in large-scale underground excavations [J]. International Journal of Rock Mechanics and Mining Sciences, 2007, 44(4): 550-564. DOI: 10.1016/j.ijrmms.2006.09.013.
[38] MONTOTO M, SUAREZ L M, KHAIR A W, HARDY H R. AE in uniaxially loaded granitic rocks in relation to their petrographic character [J]. Trans Tech Pub Clausthal, 1984: 83-100.
[39] BAKKER R R, FAZIO M, BENSON P M, HESS K, DINGWELL D B. The propagation and seismicity of dyke injection, new experimental evidence [J]. Geophysical Research Letters, 2016, 43(5): 1876-1883. DOI: 10.1002/ 2015gl066852.
(Edited by HE Yun-bin)
中文导读
基于声发射主频熵的岩爆预警实验研究
摘要:岩爆是一种伴随着声发射(AE)活动的动态现象,难以准确预测。本文基于快速傅立叶变换(FFT)方法和信息熵理论,建立了主频熵的演化模型。综合考虑应力,AE能量和频率来进行岩爆预警。在三轴卸荷的试验条件下,分析了声发射参数与裂纹发育的关系,使用FFT方法获得了AE主频分布的特征。基于信息熵理论确立了主频熵的演化模型。可以观察到,实验中的主频熵演化模型几乎都呈现出“震荡—下降—小幅上升—急剧下降”的特征。结果表明,岩爆前,AE能量会突然释放,声发射的中频密度会增加。主频熵值在岩爆前达到相对最大值,然后急剧下降。这些特征可以作为岩爆预警的前兆信息,主频熵相对最大值点可以作为预测岩爆的关键点。这对于岩爆预警是一次有意义的尝试。
关键词:岩爆;前兆信息;声发射;信息熵;主频熵;演化模型
Foundation item: Project(2017YFC0804201) supported by the National Key Research and Development Program of China; Project(51574246) supported by the National Natural Science Foundation of China; Project(2011QZ01) supported by Fundamental Research Funds for the Central Universities, China; Project(C201911362) supported by the National Training Program of Innovation and Entrepreneurship for Undergraduates, China
Received date: 2020-06-11; Accepted date: 2020-09-11
Corresponding author: WANG Chun-lai, PhD, Professor; Tel: +86-13811322376; E-mail: clwang@cumtb.edu.cn; ORCID: https://orcid. org/0000-0003-4935-4945

