Intelligent prediction on performance of high-temperature heat pump systems using different refrigerants
来源期刊:中南大学学报(英文版)2018年第11期
论文作者:于晓慧 ZHANG Yu-feng(张于峰) ZHANG Yan(张彦) 贺中禄 董胜明 马学莲 姚胜
文章页码:2754 - 2765
Key words:high-temperature heat pump; experimental performance; support vector machine; back propagation neural network; performance prediction
Abstract: Two new binary near-azeotropic mixtures named M1 and M2 were developed as the refrigerants of the high-temperature heat pump (HTHP). The experimental research was used to analyze and compare the performance of M1 and M2-based in the HTHP in different running conditions. The results demonstrated the feasibility and reliability of M1 and M2 as new high-temperature refrigerants. Additionally, the exploration and analyses of the support vector machine (SVM) and back propagation (BP) neural network models were made to find a practical way to predict the performance of HTHP system. The results showed that SVM-Linear, SVM-RBF and BP models shared the similar ability to predict the heat capacity and power input with high accuracy. SVM-RBF demonstrated better stability for coefficient of performance prediction. Finally, the proposed SVM model was used to assess the potential of the M1 and M2. The results indicated that the HTHP system using M1 could produce heat at the temperature of 130 °C with good performance.
Cite this article as: YU Xiao-hui, ZHANG Yu-feng, ZHANG Yan, HE Zhong-lu, DONG Sheng-ming, MA Xue-lian, YAO Sheng. Intelligent prediction on performance of high-temperature heat pump systems using different refrigerants [J]. Journal of Central South University, 2018, 25(11): 2754–2765. DOI: https://doi.org/10.1007/s11771-018-3951-0.

J. Cent. South Univ. (2018) 25: 2754-2765
DOI: https://doi.org/10.1007/s11771-018-3951-0

YU Xiao-hui(于晓慧)1, ZHANG Yu-feng(张于峰)1, ZHANG Yan(张彦)2, HE Zhong-lu(贺中禄)1,DONG Sheng-ming(董胜明)1, MA Xue-lian(马学莲)1, YAO Sheng(姚胜)2
1. School of Environmental Science and Engineering, Tianjin University, Tianjin 300072, China;
2. School of Architecture, Tianjin University, Tianjin 300072, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: Two new binary near-azeotropic mixtures named M1 and M2 were developed as the refrigerants of the high-temperature heat pump (HTHP). The experimental research was used to analyze and compare the performance of M1 and M2-based in the HTHP in different running conditions. The results demonstrated the feasibility and reliability of M1 and M2 as new high-temperature refrigerants. Additionally, the exploration and analyses of the support vector machine (SVM) and back propagation (BP) neural network models were made to find a practical way to predict the performance of HTHP system. The results showed that SVM-Linear, SVM-RBF and BP models shared the similar ability to predict the heat capacity and power input with high accuracy. SVM-RBF demonstrated better stability for coefficient of performance prediction. Finally, the proposed SVM model was used to assess the potential of the M1 and M2. The results indicated that the HTHP system using M1 could produce heat at the temperature of 130 °C with good performance.
Key words: high-temperature heat pump; experimental performance; support vector machine; back propagation neural network; performance prediction
Cite this article as: YU Xiao-hui, ZHANG Yu-feng, ZHANG Yan, HE Zhong-lu, DONG Sheng-ming, MA Xue-lian, YAO Sheng. Intelligent prediction on performance of high-temperature heat pump systems using different refrigerants [J]. Journal of Central South University, 2018, 25(11): 2754–2765. DOI: https://doi.org/10.1007/s11771-018-3951-0.
1 Introduction
A considerable amount of waste heat in the temperature range of 45–80 °C is being discharged in various industrial processes, which results in energy waste and environment pollution [1]. In addition, traditional method to provide heat at the temperature of 70–130 °C by burning fossil fuel is extensively used in the industrial processes, such as distillation of chemical products, food sterilization and rubber production [2, 3].
High-temperature heat pump (HTHP) can raise the temperature of the waste heat source to a higher, more useful level [4, 5]. Therefore, it is considered to have great prospect in industrial application [6]. However, HTHP is limited to heat production at a temperature of 100 °C. Therefore, the development of HTHP using suitable refrigerants to produce high output temperature represents a step to save energy and improve energy efficiency in industries [7]. One of the main problems with the development of the HTHP is the choice of refrigerant. Additionally, heat capacity, power input and coefficient of performance (COP) are of great importance for a HTHP system. Majority of researchers obtained these parameters by experimental study or practical application in engineering. Some models, such as artificial neural network (ANN) model, grey model (GM) model, multiple linear regression (MLR) and fuzzy logic inference model were proposed to predict the performance of heat pump and other systems in numerous research papers [8–13]. ANN was well-known and widely used for its ability to estimate the non-linear relationships among variables [14, 15]. However, the traditional ANN model had some drawbacks such as overfitting, local minima and curse of dimensionality. In addition, the number of observations seriously affected its accuracy. To solve these problems, Vapnik proposed support vector machine (SVM) which has shown a number of advantages on small sample size, non-linear problem and pattern recognition [16, 17]. It was extensively applied in classification of images, pattern recognition, regression analysis and so on [18–22]. According to the above analyses, further research of HTHP should pay more attention to developing new high-temperature refrigerants for getting high output temperature. Additionally, an effective and accurate method of HTHP system performance prediction is in strong demand for refrigerant selection, system optimization and development of HTHP technology.
Two refrigerants M1 and M2 were developed for HTHP which can provide heat up to 110 °C. Performance analyses and comparison of M1 and M2-based HTHP were presented in this paper using the experimental data. A SVM method was proposed to predict performance of HTHP system. The experimental data of HTHP system using M1 as refrigerant helped to establish and test the SVM-linear, SVM- radial basis kernel (RBF) and back propagation (BP) neural network models for the sake of credibility and practicability. The models were used for predicting various performance parameters of the HTHP system adopting M1, namely heat capacity, power input and COP. A comparison of experimental and predicted results was made to evaluate the accuracy of the proposed models. Additionally, the above models with good performance were used for prediction of the heat capacity, power input and COP of M2. The objective is to assess the feasibility and reliability of the presented model, which serves as a tool to predict the performance of HTHP system adopting different refrigerants. The potential of M1 and M2 as working fluid to produce a higher condensation temperature was investigated and compared based on the proposed SVM model.
2 Experimental description and analysis
2.1 Experiment setup
A HTHP system was built to study its performance on a national heat pump test bench, which is located in Dongying, Shandong province, China. Figures 1 and 2 show the flowchart and the appearance of the experimental HTHP system. There are two loops in the experimental HTHP system (refrigerant loop and water loop).

Figure 1 Flowchart diagram of HTHP system

Figure 2 Appearance of experimental HTHP system
The refrigerant loop mainly includes an evaporator, a condenser, an electronic expansion valve and two scroll compressors with lubricating oil of 320SZ. The water loop includes a heating- water system I, a cooling-water system II, a water- mixer system III and an auxiliary cooling-water system IV. Heat is transferred from the cooling- water system to the heating-water system by the water-mixer system. However, the heating-water system cannot absorb the gross heat from the cooling-water system. Therefore, an auxiliary cooling-water system with a fan coil unit is used to discharge excess heat from the cooling-water system to the environment, ensuring that the water loop operates stably [23]. Table 1 lists the apparatus parameters of the HTHP system.
2.2 Data acquisition
The experimental performances of the HTHP system using M1 and M2 as refrigerants were tested respectively. The inlet and outlet temperatures of the condenser and evaporator were set. Experimental data were recorded when the HTHP system reached its steady state, where the temperature fluctuations were smaller than ±0.3 °C and water flow rate of the heating water system and cooling water system fluctuated within a range of ±5%.
The type and accuracy of measurement instruments are shown in Table 2. An Aglient- 34970A type data acquisition and an electrical measuring instrument-8905F recorded the experimental data, and then gathered data were transferred to a personal computer through a RS232C serial interface.
Table 1 Apparatus parameters of HTHP system
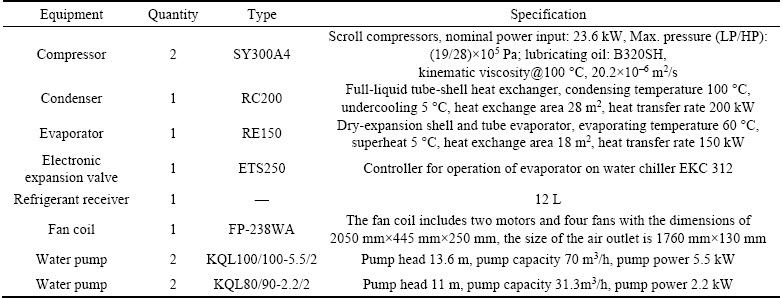
Table 2 Type and uncertainty/accuracy of instruments

2.3 Uncertainty analysis
According to the uncertainty analysis theory, the propagation of uncertainties based on the root of the sum squares is shown in Eq (1). The performance of the HTHP system is obtained by calculating data. The uncertainties of the calculated parameters are shown in Table 3.
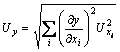 (1)
(1)
Table 3 Uncertainties of parameters

2.4 Experimental results and discussion
Experimental investigations of this HTHP using M1 and M2 as refrigerants were carried out at high temperature level of 45–70 °C on evaporation unit and 90–110 °C on condensing unit, respectively. M1 is a binary near-azeotropic mixture with a critical temperature of 150.2 °C and critical pressure of 4.44 MPa. The global warming potential (GWP) and ozone depleting potential (ODP) of M1 are 0 and 755, respectively. M2 is also a binary near-azeotropic mixture with a critical temperature of 149.1 °C and critical pressure of 4.14 MPa. The GWP of M2 is 0 and the ODP of M2 is 810. Table 4 shows part of the experimental results. The experimental results indicate the COP of M1 is higher about 11.44% than that of M2 in similar operating conditions. The main reason is that M1 has low suction and discharge pressures, which result in low power input, but the heat capacity has a little change compared with M2. The suction and discharge pressures of M1 are lower 18.85% and 18.31% than that of M2 in the similar operating conditions. M2 has high power input of about 14.98% compared with M1. Therefore, M1 with good performance and suitable pressure was selected as a high-temperature refrigerant when the temperature of the output was required to be 90–110 °C. Additionally, the performance of the HTHP system is mostly dependent on the water temperatures of the evaporation and condensing units. Every 1 °C increase of water temperature on evaporation unit can yield a 2.87% (M1) and 2.85% (M2) increase of the COP, but every 1 °C increase of water temperature on condensing unit can cause a 5.46% (M1) and 6.01% (M2) decrease of the COP. However, the COP decreases as the increase of temperature on condensing unit is nearly double the COP increase with the increase of temperature on evaporation unit. Obviously, the temperature on condensing unit greatly affects the COP compared with evaporation unit. It is also in agreement with theoretical result.
Table 4 Partly experimental results of HTHP system with different refrigerants

According to above analysis, the performance of the HTHP system is mostly dependent on the water temperatures of the evaporation and condensing units and thermo-physical properties of refrigerant.
3 Method
3.1 SVM for regression
SVM has become increasingly popular for classification and regression [22, 24, 25]. The main aim of SVM for regression (SVR, also support vector regression) is to look for a decision function that has the minimum deviation from all training data received [26]. Whereas the original problem often happens that regressions are not linear in the original space. For this reason, a non-linear SVR, which maps the original input data into a much higher-dimensional space, was developed to make the regression easier [27]. To keep the computational load reasonable, the mappings are designed to ensure that dot products may be computed easily in terms of the variables in the original input space, by defining them in terms of a kernel function selected to suit the problem [28]. In SVR, a data set is given in Eq. (2).
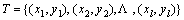 ,
,
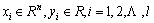 (2)
(2)
where xi is a training sample with a target value yi. For regression, the form of decision function is given:
is a training sample with a target value yi. For regression, the form of decision function is given:
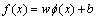 ,
, 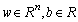 (3)
(3)
where w and b are the weight vector and the bias, respectively; f is a mapping function which maps the original input data into a higher-dimensional space.
The solution of w and b can be expressed as:
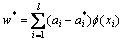 (4)
(4)
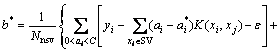
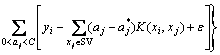 (5)
(5)
where Nnsv is the number of support vectors; ai and 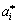 are Lagrange multipliers; k(xi, xj)=f(xi)·f(xj) is a kernel function; ε is a free parameter which serves as a threshold and all predictions must be within an ε range of the true predictions.
are Lagrange multipliers; k(xi, xj)=f(xi)·f(xj) is a kernel function; ε is a free parameter which serves as a threshold and all predictions must be within an ε range of the true predictions.
For regression, the decision function can be rewritten as follows:
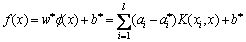 (6)
(6)
From Eq (5), the predicted COP, heat capacity and power input can be obtained.
3.2 BP neural network
The BP neural network proposed by a scientific group of Rumelhart and McCelland in 1986 was selected as traditional ANN model to compare with SVR model [29]. It is a multi-layer feedforward neural network applying BP algorithm and one of the most widely used ANN models [30]. BP neural network can asymptotically approach the ideal function and has good mapping ability on solving non-linear problem. The basic BP neural network has three layers: input layer, hidden layer (single layer or multi-layer) and output layer. Inputs from one or more neurons in the previous layer are individually weighted, and then summed. Each output of a neuron is decided by the weighted sum of all its inputs and then passed on to the neurons in the next layer. The values of the weights between neurons are adjustable and BP algorithm is a common method of adjusting the weights to solve a specific problem.
The BP learning process includes forward and backward propagating modes [31]. In the forward propagating process, the network outputs a result based on the neurons that learn from training examples, in which weights are initially random. The output is compared with the expected output and the mean squared error as a common method is used to calculate the discrepancy between them. If the desired output is obtained, the learning process will be ended; if not, the error value will be propagated backwards. Some changes of the weights in each layer are made to reduce the error. The whole process will be repeated until the overall error value drops below pre-determined threshold.
3.3 Modeling
To find a practical way to predict the performance of the HTHP system, the SVM and BP models were built, originally investigated and analyzed. Actually, the HTHP system is an organic unity and its performance is strongly dependent on several factors. Especially, the temperature conditions for the heat source and heat sink and thermo-physical properties of refrigerant are important factors. Taking all the factors into consideration, to setup and predict the HTHP system performance is very complicated and difficult. Thus, to make the case less complicated and more practical, the COP, heat capacity and power input are used as the output variables which represent the HTHP system’s performance in this paper. The inlet and outlet water temperatures of the evaporator, the inlet and outlet water temperatures of the condenser, suction pressure and discharge pressure were selected as the input variables of SVM and BP models which act as the factors affecting the performance of the HTHP system. Additionally, for the sake of credibility and practicability, the data used in the models come from the HTHP experiments.
3.3.1 Selection of training and test sets
The available data set should be divided into a training data set and a test data set. The training set is to discover potentially predictive relationships while the test set is to evaluate whether the discovered relationships can hold or not. The experimental data of the HTHP system using M1 as refrigerant helped to establish and test the proposed models. There are 77 groups of sample data for HTHP system using M1. About 70% of them (52 groups) were used for training and the rest 30% (25 groups) were used for testing.
3.3.2 Data pre-processing
Generally, data pre-processing is a very important step to reduce misleading results caused by raw data in the data mining process. In addition, the range of raw data varies widely, resulting in improper work of the objective function. Thus, we called the Mapminmax function in MATLAB to rescale the range of features in [–1, 1]. The formula is given by the following equation.
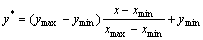 (7)
(7)
where x is an original value and y is the normalized value; ymax and ymin are two arbitrary points to restrict the range of values in the data set between ymax and ymin. We set the values of ymax and ymin to be 1 and –1 in this paper, respectively. xmax and xmin are the maximum and minimum values in the data set.
3.3.3 Parameter optimization
As a data-driven model, the effectiveness of SVR method is mostly dependent on the selection of kernel, the kernel’s parameter and penalty parameter C. The common choice for non-linearity is the RBF kernel, which has a single parameter g. In the study, K-fold cross validation (K-CV) with 5 folds was applied to optimizing the parameters. In K-CV, the original sample is randomly divided into K equal sized subsets and each is held out in turn as the validation set. Its advantage is that all subsets are used for both training and validation, and each of the k subsets is used exactly once as the validation data.
3.3.4 BP model
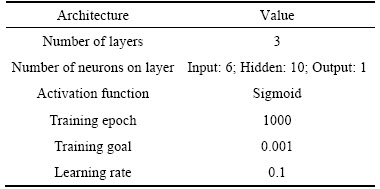
To investigate the potential of SVR in performance prediction for HTHP system, a comparison between SVR and multi-layer BP neural network models was made to evaluate the models’ performance. The parameters presented in Table 5 were selected after many trials in the multi- layer BP neural network model.
Table 5 BP neural network architecture and setting training parameters
3.3.5 Performance evaluation
The performance of the SVR-based and BP-based predictions is evaluated by a regression analysis between the predicted values and reference values, i.e., experimental values. Mean relative error (MRE), root mean square error (RMSE) and R2 (squared correlation coefficient) are the three criteria that can be applied in the evaluation. MRE indicates the mean ratio between the experimental values and the errors. R2 is a measure of how well the model fits the reference data set. The three criterions are defined as:
 (8)
(8)
 (9)
(9)
 (10)
(10)
where l is the number of the points in the data set; 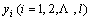 is the experimental value of the ith sample and
is the experimental value of the ith sample and 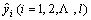 is the predicted value of the ith sample based on the presented model.
is the predicted value of the ith sample based on the presented model.
4 Results and discussion of prediction model
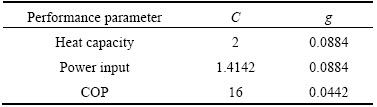
The ability of the SVR to make reasonable prediction is principally dependent on model parameter selection. The 5 folds-CV method was used to select regularization parameter (C) and unclear parameter (g) for RBF kennels. Table 6 lists the optimal values of parameters for this data set with RBF kernel-based SVR.
Table 6 Optimized C and g using K-CV
4.1 Model validation
The common linear and RBF kernels were used to explore the potential of SVR model for performance prediction of HTHP systems with M1 in this paper. The experimental data of HTHP system using M1 as refrigerant helped to establish and test the linear and RBF kernel-based SVR models. The predictions of SVR-Linear, SVR-RBF and BP models for the performance parameters of the considered HTHP system as a function of the experimental values are shown in Figures 3–5. Note that in all figures the comparisons were made using only values from the test set. The accuracy of the presented models was evaluated with the help of a straight line indicating perfect prediction and ±5% error band. MRE, RMSE and R2 served to evaluate the differences between the predicted and experimental data for the presented models. Table 6 compares the evaluation parameters of the three presented models.
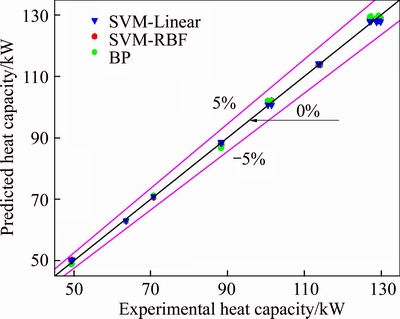
Figure 3 Performance of SVR-Linear, SVR-RBF and BP models for heat capacity prediction
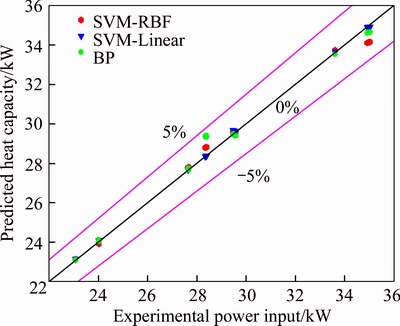
Figure 4 Performance of SVR-Linear, SVR-RBF and BP models for power input prediction
The results in Figures 3 and 4 indicated that the deviations between the results from SVM-Linear SVM-RBF and BP models from the experimental values are below ± 5% for testing sets. Combining the information shown in Table 7, conclusion can be drawn that SVM-Linear SVM-RBF and BP models share the similar ability to predict the heat capacity and power input of the HTHP system with high accuracy. Figure 5 illustrates that the SVR-RBF model performs better than SVR-Linear and BP models in predicting the COP. The error level of the SVR-RBF model is below ± 2% in the testing. It means the predicted COP based on the SVR-RBF model is in good agreement with experimental COP considering the COP uncertainty of 2.08% (see Table 4). MRE, RMSE and R2 in this model are 0.70%, 0.03 and 0.9990, respectively (see Table 3). Therefore, the simulation results validate the high efficiency of the SVR-RBF model for COP prediction.
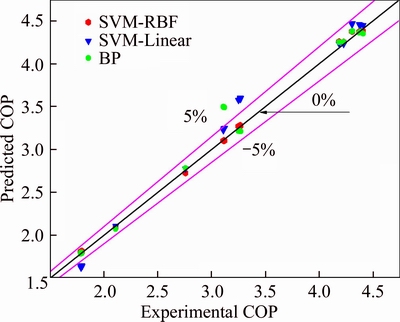
Figure 5 Performance of SVR-Linear, SVR-RBF and BP models for COP prediction
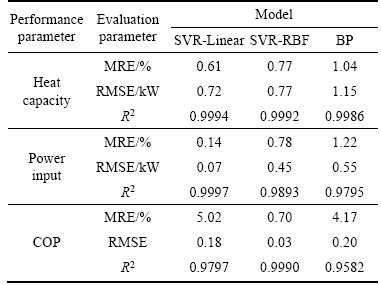
Table 7 Comparison of SVR-Linear, SVR-RBF and BP models
4.2 Performance prediction validation of M2 based on model using M1 data
This paper made further study in prediction for performance parameters of HTHP system using M2 as refrigerant based on the above presented models. The objective is to assess the feasibility and reliability of the presented model based on the data of M1, which is used to predict the performance of M2. The above analyses show that the SVR-Linear, SVR-RBF and SVR-RBF models share the similar ability to predict heat capacity and power input and the SVR-RBF model show excellent predictive performance of the COP. Therefore, the simple SVR-Linear model was used to simulating the heat capacity and power input, and SVR-RBF model was applied to simulate the COP for the HTHP system using M2 as working fluid. The predictions for the performance parameters of the HTHP system adopting M2 as a function of the experimental values are given in Figures 6–8 based on the presented SVR-Linear and SVR-RBF models.
Figure 6 shows a plot of the predicted values versus experimental data for the heat capacity. The error level of the model is below ±20 % in the case. The SVR-Linear model in the heat capacity prediction products a MRE of 11.62, RMSE of 9.88 kW and R2 of 0.9918. Figure 7 presents a plot of the predicted values versus experimental data for the power input. The power input prediction using the presented SVR-Linear model yields a MRE of 0.38, RMSE of 0.15 kW and R2 of 0.9991 with the experimental data. Figure 8 gives a plot of the predicted values versus experimental data for the COP. As shown in Figure 8, the SVR-RBF model in the COP prediction obtains a MRE of 6.26, RMSE of 0.21 and R2 of 0.9856. The error level of the model is below ±20 % (ranging from –0.22% to 16.19%) in the case.
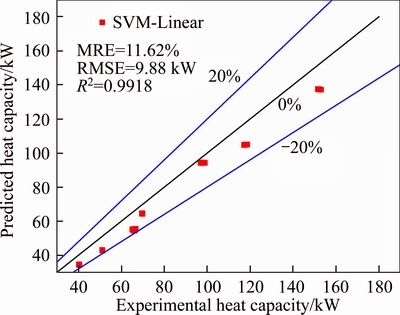
Figure 6 Comparison of experimental and predicted heat capacity using SVR-Linear model
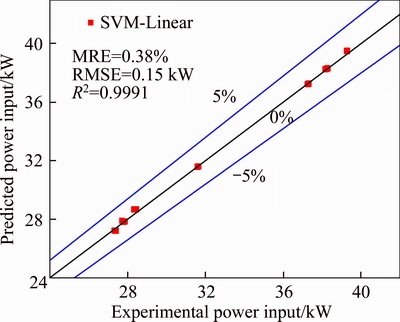
Figure 7 Comparison of experimental and predicted power input using SVR-Linear model
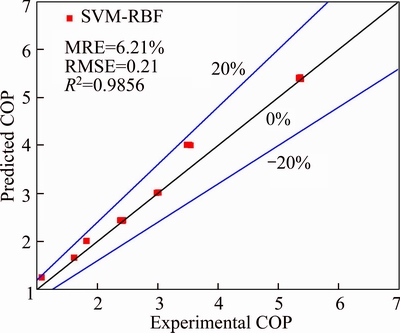
Figure 8 Comparison of experimental and predicted COP using SVR-RBF model
The simulation results demonstrate that the performance of the SVR-Linear model to predict the power input from the HTHP system using M2 is satisfactory despite the model was built based on experimental data of the refrigerant M1. The model predictions in heat capacity and COP are slightly poorer than the previous prediction for the heat capacity and COP of HTHP system using M1. The uncertainties of the COP (2.02%) and heat capacity (2.08%) and a low number of experimental data for training partly lead to the relative high prediction error. The prediction accuracy of SVM model with error of below ±20 % is acceptable for the engineering application of the HTHP system. Therefore, the results indicated the presented model is feasible and reliable to predict the heat capacity and COP of HTHP system using different refrigerants. It means that the presented SVR method is potential to predict the performance of HTHP with different refrigerants, which is helpful in refrigerant selection, system optimization and development of HTHP technology. Manufactures and researcher of HTHP systems determine their performance parameters easily without requiring exhaustive experiments by the method of appropriately using SVR. In additional, the presented SVR method, which can derive the function of the performance parameters and the input variables, can serve as an analyzing tool to optimize and design HTHP systems.
4.3 Performance evaluation and comparison of M1 and M2 based on SVM model
The potential of the HTHP system using M1 and M2 as working fluid to produce a higher heating temperature was investigated by estimating the heat capacities, power inputs and COPs based on the above presented SVM model. Figure 9 show the performance comparison of M1 and M2 based on the SVM model when the evaporation temperature is 65–85 °C and the condensation temperature is 120 °C and 130 °C, respectively.
As seen in Figure 9(a), higher evaporation temperature achieves higher heat capacity and higher condensation temperature results in a lower heat capacity which is no surprise. The suction density and the mass flow rate of working fluid increase with the condensation and evaporation temperature, which leads the increase of the heating capacity. The heat capacity of M1 is lower than that of M2 at a low condensation temperature due to the high latent heat of M2, but the heat capacity of M1 is slightly higher than that of M2 when the condensation temperature exceeds 120 °C. Some of this is due to the fact that the latent heat difference between M1 and M2 decreases with the increase of the condensation temperature.
Figure 9(b) shows that the power input of M1 is considerably low compared with M2 in the same high-temperature running conditions. It is due to the high pressure and compressor ratio of M2 compared with that of M1. Every 1 °C increase of condensation temperature can yield an about 1.24% increase of the power input, but every 1 °C increase of evaporation temperature can result in an about 0.27% decrease of the power input. Therefore, the condensation temperature has a significant impact on the power input. Some of this is due to the fact that the increase of the discharge pressure with the condensation temperature is important compared with the increase of the suction pressure with the evaporation temperature. In addition, the compressor heat loss rapidly rises with the increase of the condensation temperature that is much higher than environmental temperature.

Figure 9 Performance comparison of M1 and M2 based on SVM model:
Figure 9(c) presents that the COP of M1 is superior to that of M2 in different high-temperature conditions. The low power input is main reason for M1 with superior COP. The COP of M1 and M2 is higher than 3 at the condensation temperature of 120 °C when the evaporation temperature is higher than 77. The COP of is 3.48 at the evaporation temperature of 85°C and condensation temperature of 130 °C. Thus, the HTHP system using M1 as working fluid has potential to attain a condensation temperature of 120–130 °C with good performance.
5 Conclusions
In this paper, two new binary near-azeotropic mixtures named M1 and M2 were proposed as the refrigerants of the HTHP system. The experimental research was used to analyze and compare the performance of M1 and M2-based the HTHP at high temperature level of 45–70 °C on evaporation unit and 90–110 °C on condensing unit. The experimental results demonstrated the feasibility and reliability of M1 and M2 as new high-temperature refrigerants. To find a practical way to predict the performance of the HTHP system, the potential of SVM and BP models to predict the performance of HTHP system was originally investigated and analyzed. For the sake of practicability and credibility, the data used in the models came from the HTHP experiments. Additionally, the potential of the HTHP system using M1 and M2 to produce higher heating temperature was also assessed by the proposed models with good performance. The following conclusions can be drawn:
1) Compared with M2, M1 is selected as the working fluid of HTHP system when the heating temperature was in the range of 90–110 °C due to its superior thermal and economic performance.
2) SVM-Linear, SVM-RBF and BP models share the similar ability to predict the heat capacity and power input of the HTHP system with high accuracy and the SVR-RBF model performs well in predicting the COP of HTHHP system compared with SVM-RBF and BP models.
3) The presented SVM model based on the data of M1 is feasible and reliable to predict the performance parameters of M2.
4) The HTHP system using M1 as refrigerant had the potential to attain a condensation temperature of 130 °C with good performance when the evaporation temperature is higher than 85 °C.
References
[1] WANG Zhi-qi, ZHOU Qi-yu, XIA Xiao-xia, LIU Bin, ZHANG Xin. Performance comparison and analysis of a combined power and cooling system based on organic Rankine cycle [J]. Journal of Central South University, 2017, 24(2): 353–359.
[2] Adri n M, Joaqu
n M, Joaqu n N,
n N,  ngel B, MOL
ngel B, MOL S F, PERIS B. Experimental study of an R1234ze(E)/R134a mixture (R450A) as R134a replacement [J]. International Journal of Refrigeration, 2015, 51: 52–58.
S F, PERIS B. Experimental study of an R1234ze(E)/R134a mixture (R450A) as R134a replacement [J]. International Journal of Refrigeration, 2015, 51: 52–58.
[3] PAN Li-sheng, WANG Huai-xin, CHEN Qing-ying, CHEN Chen. Theoretical and experimental study on several refrigerants of moderately high temperature heat pump [J]. Applied Thermal Engineering, 2011, 31: 1886–1893.
[4] ZHANG Yan, ZHANG Yu-feng, YU Xiao-hui, GUO Jing, DENG Na, DONG Sheng-ming, HE Zhong-lu, MA Xue-lian. Analysis of a high temperature heat pump using BY-5 as refrigerant [J]. Applied Thermal Engineering, 2017, 127: 1461–1468.
[5]  arevski M.
arevski M.  arevski V. Thermal characteristics of high-temperature R718 heat pumps with turbo compressor thermal vapor recompression [J]. Applied Thermal Engineering, 2017, 117: 355–365.
arevski V. Thermal characteristics of high-temperature R718 heat pumps with turbo compressor thermal vapor recompression [J]. Applied Thermal Engineering, 2017, 117: 355–365.
[6] Ozyurt O, Comakli O, Yilmaz M, KARSLI S. Heat pump use in milk pasteurization: an energy analysis [J]. International Journal of Energy Research, 2004, 28: 833–846.
[7] Marwan C, Romuald R, Philippe H, JEAN L. Experimental and numerical investigations of a new high temperature heat pump for industrial heat recovery using water as refrigerant [J]. International Journal of Refrigeration, 2014, 44: 177–188.
[8] ZENG Yi-hui, LIU Shao-jun, E Jia-qiang. Neuron PI control for semi-active suspension system of tracked vehicle and its application [J]. Journal of Central South University of Technology, 2011, 18(2): 444–450.
[9] WANG Shuang-ying, ZUO Hong-yan. Safety diagnosis on coal mine production system based on fuzzy logic inference [J]. Journal of Central South University of Technology, 2012, 19(2): 477–481.
[10] ZUO Hong-yan, LUO Zhou-quan, GUAN Jia-lin, WANG Yi-wei. Multidisciplinary design optimization on production scale of underground metal mine [J]. Journal of Central South University, 2013, 20(5): 1332–1340.
[11] ESEN H, INALLI M, SENGUR A, ESENA M. Predicting performance of a ground-source heat pump system using fuzzy weighted pre-processing-based ANFIS [J]. Building and Environment, 2008, 43(12): 2178–2187.
[12] YANG Hai-dong, E Jia-qiang, QU Ting. Multidisciplinary design optimization for air-condition production system based on multi-agent technique [J]. Journal of Central South University of Technology, 2012, 19(2): 527–536.
[13] E Jia-qiang, LI Yu-qiang, GONG Jin-ke. Function chain neural network prediction on heat transfer performance of oscillating heat pipe based on grey relational analysis [J]. Journal of Central South University of Technology, 2011, 18(5): 1733–1737.
[14] Esen H, Inalli M, Sengur A, Esena M. Forecasting of a ground-coupled heat pump performance using neural networks with statistical data weighting pre-processing [J]. International Journal of Thermal Sciences, 2008, 47(4): 431–441.
[15] Mohanraj M, Jayaraj S, Muraleedharan C. Performance prediction of a direct expansion solar assisted heat pump using artificial neural networks [J]. Apply Energy, 2009, 86: 1441–1449.
[16] Vapnik V. The nature of statistical learning theory [M]. New Work: Springer Verlag,1995.
[17] Vapnik V. Statistical learning theory [M]. New Work: John Wiley & Snos, 1998.
[18] WANG Tao-sheng, ZUO Hong-yan. Fuzzy least squares support vector machines soft measurement model based on adaptive mutative scale chaos immune algorithm [J]. Journal of Central South University, 2014, 21(2): 593–599.
[19] ZUO Hong-yan, LUO Zhou-quan, GUAN Jia-lin, WANG Yi-wei. Identification on rock and soil parameters for vibration drilling rock in metal mine based on fuzzy least square support vector machine [J]. Journal of Central South University, 2014, 21(3): 1085–1090.
[20] E Jia-qiang, QIAN Cheng, ZHU Hao, PENG Qing-guo, ZUO Wei, LIU Guan-lin. Parameters identification investigations on the hysteretic Preisach model improved by the fuzzy least square support vector machine based on adaptive variable chaos immune algorithm [J]. Journal of Low Frequency Noise, Vibration and Active Control, 2017, 36(3): 227–242.
[21] E Jia-qiang, ZUO Qing-song, LIU Hai-li, LI Yu, GONG Jin-ke. Endpoint forecasting on composite regeneration by coupling cerium-based additive and microwave for diesel particulate filter [J]. Journal of Central South University, 2016, 23(8): 2118-2128.
[22] Dhanalakshmi P, Palanivela S, Ramalingama V. Classification of audio signals using SVM and RBFNN [J]. Expert Systems with Applications, 2009, 36(3): 6069–6075.
[23] YU Xiao-hui, ZHANG Yu-Feng, DENG Na, CHEN Cheng-min, MA Li-jun, DONG Li-pin, ZHANG Yan. Experimental performance of high temperature heat pump with near-azeotropic refrigerant mixture [J]. Energ Buildings, 2014, 78: 43–49.
[24] DONG Sheng-ming, ZHANG Yu-feng, HE Zhong-lu, DENG Na, YU Xiao-hui, YANG Sheng. Investigation of support vector machine and back propagation artificial neural network for performance prediction of the organic Rankine cycle system [J]. Energy, 2018, 144: 851–864.
[25] Jadran B, Eva O, DALIBOR C, GORAN L. Application of neural networks and support vector machine for significant wave height prediction [J]. Oceanologia, 2017, 59: 331–349.
[26] Shamshirband S, Petkovi D, Amini A, ANUAR N, NIKOLI
D, Amini A, ANUAR N, NIKOLI V,
V,  OJBASI
OJBASI
 , KIAH L, CANI A. Support vector regression methodology for wind turbine reaction torque prediction with power-split hydrostatic continuous variable transmission [J]. Energy, 2014, 67: 623–630.
, KIAH L, CANI A. Support vector regression methodology for wind turbine reaction torque prediction with power-split hydrostatic continuous variable transmission [J]. Energy, 2014, 67: 623–630.
[27] TIAN Ying-jie. Support vector regression and its application [D]. Beijing: China Agricultural University, 2005. (in Chinese)
[28] Press W, Saul A, William T, FLANNERY B. Numerical recipes: The art of scientific computing, Section 16.5. Support Vector Machines [M]. 3rd ed. New York: Cambridge University Press, 2007.
[29] Zhang Jian-qing. Study on the gas content of coal seam based on the BP neural network [J]. Procedia Engineering, 2011, 26: 1554–1562.
[30] LI Ming-shun, CHEN Wen-cui. Application of BP neural network algorithm in sustainable development of highway construction projects [J]. Procedia Engineering, 2012, 25: 1212–1217.
[31] TIAN Jing-wen, GAO Mei-juan. Research and application of artificial neural network algorithm [M]. Beijing: Beijing Institute of Technology Press, 2006. (in Chinese)
(Edited by YANG Hua)
中文导读
不同工质的高温热泵系统性能智能预测
摘要:本文设计、开发了两种新型高温近共沸混合工质M1和M2。实验研究了不同工况下M1和M2两种工质的性能并进行对比分析。测试结果验证了M1和M2作为新型高温工质的可行性和可靠性。此外,本文还应用支持向量机及BP人工神经网络模型对高温热泵性能进行预测。预测结果表明:对于制热量和输入功率的预测,SVM-RBF、SVM-LF和BP三种模型均具有较高的预测精度,对于性能系数的预测,SVM-RBF模型具有较好的预测精度。最后,本文使用支持向量机模型对M1和M2两种工质的潜力进行评估。评估结果表明,M1的高温热泵在产热温度为130℃时仍具有良好的性能。
关键词:高温热泵;实验性能;支持向量机;误差回传神经网络;性能预测
Foundation item: Project(2015CB251403) supported by the National Key Basic Research Program of China (973)
Received date: 2017-07-23; Accepted date: 2018-04-03
Corresponding author: YU Xiao-hui, PhD, Associate Professor; Tel: +86-22-27890131; E-mail: yuxiaohui@tju.edu.cn; ORCID: 0000- 0002-6791-8946

