J. Cent. South Univ. (2012) 19: 1317-1321 

DOI: 10.1007/s11771-012-1144-9

Scattering loss in optical waveguide with trapezoidal cross section

PENG Wen-qiang(彭文强), WU Yu-lie(吴宇列), LIU Yong(刘勇), YIN Zhi-qiang(尹自强)

College of Mechatronics Engineering and Automation,

National University of Defense Technology, Changsha 410073, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2012

Abstract: To get the scattering loss of the trapezoidal core waveguide, a new analysis model is presented based on the perturbation equivalent method and modified effective-index method. Firstly, the trapezoidal core waveguide is successfully equivalent to the rectangular one with both restricting the same optical field energy by adopting the perturbation method. Then, the equivalent rectangular core waveguide is decomposed into two slab waveguides by employing the modified effective-index method. The trapezoidal core waveguide scattering theory model is established based on the slab waveguide scattering theory. With the sidewalls surface roughness in the range from 0 to 100 nm in the single model trapezodial core waveguide, optical simulation shows excellent agreement with the results from the scattering loss model presented. The relationship between the dimension and side-wall roughness with the scattering loss can be determined in the trapezoidal core waveguide by the scattering loss model.

Key words: trapezoidal core waveguide; perturbation equivalent method; modified effective-index method; scattering loss

1 Introduction

For the side etch effect in the optical waveguide manufacture process in the chemical etching and reactive ion etching, the trapezoidal cross section waveguide can be easily received. Since these methods have been widely used, the trapezoidal core waveguide is one of the basic structures in the optical waveguide devices. The side-wall roughness is formed in the manufacture process, so the scattering loss induced by the surface roughness is inevitably generated [1-3]. It is well known that scattering losses are smaller in wide and flat waveguides as the field overlap becomes smaller on the rough sidewalls [3-4]. Thus, the waveguide scattering loss is determined by the sidewall roughness and the waveguide dimensions. The scattering loss is the fundamental factor that affects the performance of the optical waveguide devices [5-8]. In general, the numerical methods offer a higher degree of accuracy and can be applied to graded index structure devices. However, to the best of the authors’ knowledge, there still is not a reliable numerical theory for trapezoidal core waveguide scattering loss analysis. The boundary condition of the trapezoidal core waveguide is complex and the accurate analysis of its propagation character is difficult [9-10]. For rectangular core waveguides, either simple approximate technique or more sophisticated numerical methods have been employed in calculating the propagation properties [11-12].

The purpose of this work is to propose an effective numerical method to establish the theory model on the trapezoidal core waveguide scattering loss. In the method, the trapezoidal core waveguide is replaced by the equivalent rectangular core waveguide. The equivalent rectangular core waveguide is then decomposed into two slab waveguides. From the slab scattering loss theory, the trapezoidal core waveguide scattering model caused by the sidewall roughness and the dimension is successfully established.

2 Perturbation equivalent method

Trapezoidal core waveguide cross section is shown in Fig. 1(a). In this figure, n₁ and n₂ are the core and cladding refractive indexes; h is the waveguide height; a₁ and a₂ are the waveguide top and bottom width. The trapezoidal core waveguide is modeled by the rectangular core waveguide of width w, and has the same height as the trapezoidal core waveguide shown in    Fig. 1(b). The equivalent waveguide has the same propagation constant and ability to restrict field energy with the original trapezoidal core waveguide. The width of the equivalent rectangular structure is determined by the perturbation equivalent method.

According to the rectangular core waveguide theory,

the fields of the equivalent rectangular core waveguide can be gotten as follows:

                         (1)

where f_x(x) and f_y(y) are the x- and y-direction field distribution functions, and can be written as

      (2)

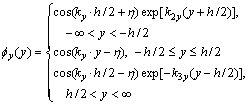      (3)

where k_x and k_y are the propagation constants in the x- and y-directions; ξ and η are integration constants.

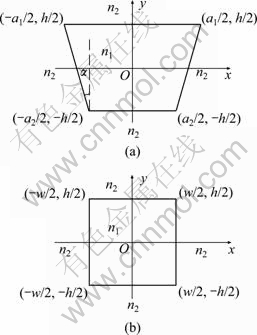
Fig. 1 Cross sections of trapezoidal (a) and equivalent rectangular (b) core waveguide

The perturbation equivalent method relies on the observation that perturbation contributions from areas S₁ and S₂ are negative and positive to propagation constant of the equivalent rectangular core waveguide, respectively, as shown in Fig. 2 [13]. So, if we sequentially shift the width of rectangular core waveguide to perturbation contribution for the propagation constant, the equivalent width, a_eq, can be obtained when perturbation contribution reaches zero. The equivalent waveguide has the same propagation constant and ability to restrict field energy with the original trapezoidal core waveguide.

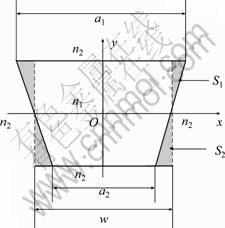
Fig. 2 Theory model of perturbation method

The field distribution function f(x, y) and propagation constant β of the trapezoidal core waveguide satisfy the Helmholtz equation and can be written as [1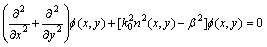4]

   (4)

From the perturbation equivalent method analysis, we know that the perturbation contribution is effective only in shadow areas shown in Fig. 2. As the second- order field distribution is small, we usually use the first- order field f₀(x, y) to modify the trapezoidal propagation constant and the modified amount ?β² can be written as

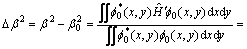
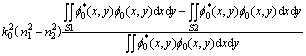            (5)

If we sequentially shift the width of rectangular core waveguide to make perturbation contribution zero for the propagation constant, then the width of the equivalent rectangular core waveguide is obtained. In the equivalent condition, the modified amount ?β² is zero and we can get

    (6)

Inserting the rectangular core waveguide field distribution function from Eq. (1) and using Eq. (6), we have the perturbation equivalent equation:

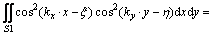
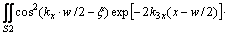
                     (7)

With Eq. (7), we can derive an equivalent rectangular core waveguide to model any trapezoidal cross section core waveguide.

3 Modified effective-index method

With modified effective-index methods, any rectangular core waveguide can be precisely equivalent to two related slab waveguides. The modified effective-index method is illustrated in Fig. 3. The rectangular core waveguide is effectively equivalent to two slab waveguides b and c. The effect refractive index N of Slab b is the core refractive index of Slab c according to Helmholtz equation. Meanwhile, the cladding refractive indexes of Slab c are modified by the effect refractive index N and the modified cladding indexes N₃ and N₅ can be written as [15]

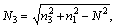
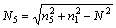        (8)

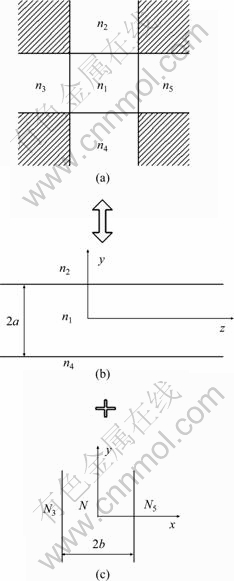
Fig. 3 Rectangular core waveguide equivalent to two slab waveguides

So, the slab waveguide b can do some modification to the propagation of slab waveguide c according to   Eq. (8). Therefore, the equivalent rectangular core waveguide can be precisely equivalent to two related slab waveguides by the modified effective-index method.

4 Scattering loss of trapezoidal core waveguide

The symmetry slab waveguide propagation model is illustrated in Fig. 4. In this figure, n₁ and n₂ are the core and cladding refractive indexes; 2d is the width of the slab waveguide; σ is the sidewalls root-mean-square (RMS) roughness; β is the propagation constant. The scattering loss coefficient of the slab waveguide caused by the exponential sidewall roughness can be written as

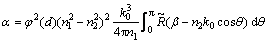   (9)

where φ(a) is optical field at the waveguide sidewalls; k₀ is free-space wave-number; λ₀ is the propagation wavelength in the vacuum.  is the spectral density function describing the surface roughness of the sidewalls; θ is the scattering angle with the propagation axes.

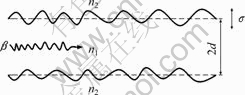
Fig. 4 Propagation model of symmetry slab waveguide

After some analytical calculations, the scattering loss coefficient in decibels per centimeter can be written as [16]

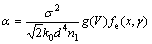                   (10)

where g(V) is a function depending only on the waveguide geometry with the normalized coefficients. The function f_e(x, y) is linked to the sidewall roughness.

Equation (10) shows that the propagation loss coefficient is linked to the roughness parameter and geometry parameters of the waveguide. According to perturbation equivalent method and modified-index method, the trapezoidal core waveguide can be equivalent to two slab waveguides. So, with the slab waveguide loss theory, the scattering loss coefficient of trapezoidal core waveguide can be written as

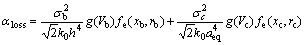       (11)

where σ_b and σ_c are the roughness of the trapezoidal core waveguide sidewalls; h and a_eq are the geometry parameters in equivalent rectangular core waveguide of trapezoidal core waveguide. So, with the slab waveguide scattering loss theory model, the scattering loss of the equivalent rectangular core waveguide can be obtained and the scattering property of the trapezoidal core waveguide can also be known.

5 Numerical simulation analysis

According to the perturbation equivalent method and modified effective-index method, we used the slab waveguide scattering loss model to establish the trapezoidal scattering model. To validate the credibility of the model, we introduced the single model trapezoidal core waveguide for scattering analysis. The core and cladding refractive indexes are 1.56 and 1.48 at the wavelength of 1 550 nm. The cross section dimensions are 12 μm and 7 μm in top and bottom width and 9 μm in height. With perturbation equivalent method, the trapezoidal core waveguide is equivalent to rectangular core waveguide with width of 8.6 μm and height of 9 μm. With modified effective-index method and slab waveguide scattering loss model, the trapezoidal core waveguide loss at different sidewall surface roughness was analyzed. Meanwhile, the trapezoidal core waveguide optical simulation at the same condition was conducted by the Beamprop software. The Beamprop simulation model is shown in Fig. 5.

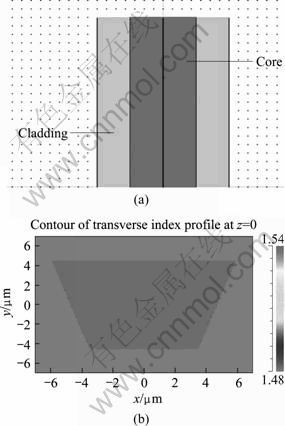
Fig. 5 Simulation model of trapezoidal core waveguide

The theory and simulation results are shown in  Fig. 6. The trapezoidal core waveguide with the sidewalls surface roughness ranging 0-100 nm is assumed for the calculations. From Fig. 6, we can see that the theory results agree well with the simulation results. So, the credibility of the model has been validated. In Fig. 6, the simulation results are a little larger than the theory model because the simulation takes the effect of the launch field coupling and Fresnel reflection loss in calculation into consideration. From the analysis, we know that the sidewall surface roughness of the trapezoidal core waveguide has great influence on the scattering loss.

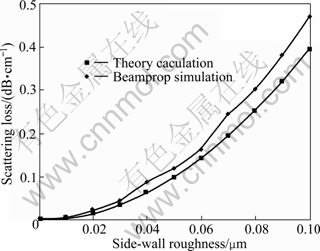
Fig. 6 Scattering loss of trapezoidal core waveguide

6 Conclusions

1) Combined with the perturbation equivalent method and the modified effective-index method, the trapezoidal core waveguide scattering loss theory model has been developed based on the slab scattering loss theory.

2) Optical simulation validates the credibility of the scattering model and shows that the sidewall roughness has great influence on the performance of the trapezoidal core waveguide.

3) The scattering loss model provides important guidance for the design of useful trapezoidal core waveguide cross sections that minimize scattering losses for practical roughness statistics.

References

[1] LEE K K, LIM D R, LUAN H C, AGARWAL A, FORESI J, KIMERLING L C. Effect of size and roughness on light transmission in a Si/SiO₂ waveguide: Experiment and model [J]. Applied Physics Letters, 2000, 77(1): 1617-1619.

[2] KUAN P Y, ANDR? D, JEAN L, BORIS L, JENS H S, PHILIP W, BARRY A S, SIEGFRIED J. Correlation of scattering loss, sidewall roughness and waveguide width in silicon-on- insulator (SOI) ridge waveguides [J]. Journal of Lightwave Technology, 2009, 27(8): 3999-4008.

[3] BARWICZ T, HAUS H A. Three-dimensional analysis of scattering losses due to sidewall roughness in microphotonic waveguides [J]. Journal of Lightwave Technology, 2005, 23(9): 2719-2732.

[4] GRILLOT F, VIVIEN L, LAVAL S, PASCAL D, CASSAN E. Size influence on the propagation loss induced by sidewall roughness in ultrasmall SOI waveguides [J]. IEEE Photonics Technology Letters, 2004, 16(7): 1661-1663.

[5] KEHINDE O L D, FRANK P P. Impact of waveguide sidewall roughness on the output uniformity and phase of MMI splitters [J]. Opt Quant Electron, 2008, 40: 863-873.

[6] LADOUCEUR F, LOVE J D, SENDEN T J. Effect of side wall roughness in buried channel waveguides [J]. IEE Proc-Optoelectron, 1994, 141(4): 242-248.

[7] HUANG B, CHEN J, JIANG W S. Effects of surface roughness on the modes in rectangular core waveguide [J]. Journal of Infrared Milli Terahz Waves, 2009, 30: 717-726.

[8] SPARACIN D K, SPECTOR S J, KIMERLING L C. Silicon waveguide sidewall smoothing by wet chemical oxidation [J]. Journal of Lightwave Technology, 2005, 23(8): 2455-2461.

[9] TSAO S L, WU J S, HER Y L. Triangular-element finite-element analysis of a trapezoid polymer optical waveguide [J]. Microwave and Optical Technology Letters, 1997, 15(2): 87-89.

[10] GALLAGHER J G. Mode dispersion of trapezoidal cross-section dielectric optical waveguides by the effective-index method [J]. Electronics Letters, 1979, 15(23): 734-735.

[11] AHMED A A. An optimal method to study the propagation characteristics of rectangular optical waveguides [C]// 15th National Radio Science Conference. Egypt, 1998: 1-6.

[12] CHIANG K S, KWAN C H, LO K M. Effective-index method with built-in perturbation correction for the vector modes of rectangular-core optical waveguides [J]. Journal of Lightwave Technology, 1999, 17(4): 716-722.

[13] CLARK D F, DUNLOP I. Method for analysing trapezoidal optical waveguides by an equivalent rectangular rib waveguide [J]. Electronics Letters, 1998, 24(23): 1414-1415.

[14] ZHAO Shan. High order matched interface and boundary methods for the Helmholtz equation in media with arbitrarily curved interfaces [J]. Journal of Computational Physics, 2010, 229: 3155-3170.

[15] KIM C M, JUNG B G, LEE C W. Analysis of dielectric rectangular core waveguide by modified effective-index method [J]. Electronics Letters, 1986, 22(6): 296-297.

[16] PAYNE F P, LACEY J P R. A theoretical analysis of scattering loss from planar optical waveguides [J]. Optical and Quantum Electronics, 1994, 26: 977-986

(Edited by YANG Bing)

Foundation item: Project(50735007) supported by the National Natural Science Foundation of China; Project(2010ZX04001-151) supported by Important National Science & Technology Specific Program of China

Received date: 2011-06-21; Accepted date: 2011-09-23

Corresponding author: PENG Wen-qiang, PhD; Tel: +86-731-84576938; E-mail: plxhaz@126.com