ARTICLE

J. Cent. South Univ. (2019) 26: 2160-2174

DOI: https://doi.org/10.1007/s11771-019-4163-y

Numerical simulation of heat release performance of filling body under condition of heat extracted by fluid flowing in buried tube

ZHANG Xiao-yan(张小艳)¹, LIU Li(刘利)¹, LIU Lang(刘浪)^{1, 2},LIU Lu(刘璐)³, JIA Yu-hang(贾宇航)¹

1. College of Energy Science and Engineering, Xi’an University of Science and Technology,Xi’an 710054, China;

2. Key Laboratory of Western Mine Exploitation and Hazard Prevention (Ministry of Education),Xi’an 710054, China;

3. College of Safety Science and Engineering, Xi’an University of Science and Technology,Xi’an 710054, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019

Abstract: It is the basic requirement of the synergetic exploitation of deep mineral resources and geothermal resources to arrange the heat transfer tube in filling body. The heat release performance of filling body directly impacts on the exploiting efficiency of geothermal energy. Based on heat transfer theory, a three-dimensional unsteady heat transfer model of filling body is established by using FLUENT simulation software. Taking the horizontal U-shaped buried pipe as research object, the variation of temperature field in filling body around buried pipe is analyzed during the heat release process of filling body; the initial temperature of filling body, the diameter of buried pipe, the inlet temperature and inlet velocity of heat transfer fluid influencing of coupling heat transfer, which exists between heat transfer fluid and surrounding filling body within a certain axial distance of buried tube, and influencing of temperature difference between inlet and outlet of heat transfer fluid and on heat transfer performance of filling body are also discussed. It not only lays a theoretical foundation for the synergetic exploitation of mineral resources and geothermal energy in deep mines, but also provides a reference basis for the arrangement of buried pipes in filling body as well as the selection of working conditions for heat transfer fluid.

Key words: filling body; buried pipe; heat transfer fluid; heat release performance

Cite this article as: ZHANG Xiao-yan, LIU Li, LIU Lang, LIU Lu, JIA Yu-hang. Numerical simulation of heat release performance of filling body under condition of heat extracted by fluid flowing in buried tube [J]. Journal of Central South University, 2019, 26(8): 2160-2174. DOI: https://doi.org/10.1007/s11771-019-4163-y.

1 Introduction

The large-scale development of the global economy greatly depends on the mining industry and deep mining becomes evitable with the continuous development of mineral resources [1-4]. The issues of thermal damage have currently become more and more serious and attracted much attention for people with the exploitation of deep mineral resources in recent years. However, the high geothermal heat that leads to the occurrence of thermal damage in mines has provided favorable conditions for geothermal exploitation. Therefore, it is a hot research topic to rationally develop and utilize geothermal resources and effectively alleviate the thermal damage in deep mines. MENNDEZ et al [5] researched that the under- ground closed mine can be applied to storing heat energy for reuse, as well as for geothermal power generation. A geothermal recycling system for mines (GRSM) for parallel mine cooling and surface heating was presented by GUO et al [6], and the performance of this system was investigated based on the observed data.NIU [7] designed an integrated system of mine cooling and mine thermal energy utilization taking high-temperature mine as the research object, and realized the recycling of energy. LU et al [8] proposed a new process of recycling waste tailings into underground and open stope as cemented paste backfill (CPB). DONG et al [9] analyzed the mining strategy of clean production in deep mines. BAO et al [10] reported a real geothermal energy application in the US for the use of water in flooded mines for house heating. CHEN et al [11] studied the effects of using phase change materials (PCMs) as grout on the efficiency of a ground source heat pump (GSHP) system, and established a numerical GSHP system model, considering both the site conditions and dynamically changing loads regulated by the heat pump. CHEN et al [12] raised the adsorption and cooling system for deep well of heat storage filling body, which can provide a reference for solving the problem of mine thermal damage by filling mining method. ZHANG et al [13] studied that filling the goaf with slurry mixed with ice grains can effectively solve the problems of high temperature thermal environment and solid waste in deep mine. WANG et al [14] investigated a cold load and storage (CLS) functional backfill method, that is to say, adding a cold load/storage medium with cooling performance into the filling material to achieve stope cooling. Aiming at the shortcomings of the current mine cooling measures, a heat pipe cooling and dehumidification air conditioning system based on the integrated recycling of heat source in coal mines was analyzed by ZHANG et al [15].

As an eco-friendly technology that uses renewable energy, heat pump can convert low-grade heat energy into high-grade heat energy and has been widely used in geothermal development [16]. One of the most key components affecting the efficiency of geothermal development system is the underground heat exchanger that can be concerned better than other parts in the development of geothermal resources. GHOREISHI-MADISEH et al [17] evaluated the possibility of the novel idea of installing geothermal heat exchange tubes in backfilled mine stopes prior to backfill placement for the purpose of geothermal heat extraction. Taking into account the effect of the air-soil boundary condition and the thermal interference between the different portions of pipes in the buried field, an analytical model of horizontal heat exchangers was presented by LAMARCHE [18]. KERME et al [19] presented the analysis, simulation and performance study of heat transfer in a single U-tube borehole heat exchanger (BHE). KONG et al [20] investigated thermal performance of ground heat exchanger (GHE) with a set of designed U-tubes by using experimental measurements and computational fluid dynamics (CFD) simulation. KAYACI et al [21] researched transient soil temperature distribution of horizontal buried heat exchanger of ground source heat pump by carrying out a numerical simulation. AL- AMEEN et al [22] investigated the possibility of recycling low cost construction and industrial waste landfills materials as potential backfills in horizontal ground heat exchangers (HGHE). JI et al [23] analyzed the impact of load distribution on ground heat exchanger under thermal equilibrium between heat extraction and heat release. Taking horizontal spiral buried tube heat exchanger as object, YANG et al [24] analyzed the influence of groundwater seepage velocity, groundwater level, soil porosity and soil type on its heat exchange and the temperature distribution of surrounding soil. Taking into account different initial soil temperatures and physical properties at different depths, CHEN et al [25] presented a numerical heat transfer model for vertical U-tube ground heat exchangers (GHE). ZHOU et al [26] studied heat transfer performance of buried pipe heat exchanger with twisted tape inserts in the backfill materials. Based on the used deep-buried coaxial double-pipe heat exchange systems for closed loop heat extraction, LI et al [27] analyzed the influence of several inner pipe types on the heat transfer performance of buried pipe systems. The three- dimensional steady state heat transfer performance of single-port and multi-port U-shaped buried tube wells was investigated by LV et al [28], and the effects of inlet velocity, temperature and other factors on its heat release performance were analyzed respectively. At present, there were many correlated researches on the heat transfer between underground heat exchanger, soil or backfill material in related filed.

Filling mining is a promising alternative for the disposal of tailings and it can also enhance ore recovery by the excavation of massive pillars, improve mining conditions by ensuring the stability of underground voids, and minimizing surface subsidence, which benefits to promote the wide application of filling mining in underground mines [29-32]. Based on the technology of filling mining, the concept of synergetic exploitation of deep mineral resources and geothermal energy is proposed, and heat transfer pipes are arranged in the filling body to extract geothermal energy. In this case, the heat transfer between the fluid in buried tube and the filling body plays a significant influence on the efficiency of geothermal energy extraction. According to the theory of heat transfer, taking the horizontal single U-shaped pipe embedded in the filling body as the research object, the numerical simulation study on heat release process of filling body under different conditions is carried out by applying FLUENT software. The main factors influencing the heat release process of filling body under the conditions of deep mining stope are analyzed, and the influence mechanism and influence law of various factors on the heat release performance and heat extraction effect of filling body are obtained. It provides theoretical reference for the research on the heat release process of filling body under the condition of heat extracted by fluid flowing in buried tube in deep mines, and it also provides a theoretical basis for the synergetic mining of deep mineral resources and geothermal.

2 Physical and numerical model

2.1 Physical model of heat release process of filling body

Figure 1 shows the physical model of heat release process for filling body. In the process of heat release, the heat transfer fluid (water) in buried pipe continuously absorbs the accumulated heat of filling body and the temperature gradually increases, meanwhile, the internal temperature of filling body gradually decreases until the end of heat release process. The heat transfer fluid will be pumped with heat extraction or heat utilization device such as a heat pump. The heat exchange process involves three parts: the convective heat transfer between heat transfer fluid and the inner wall of buried pipe, heat conduction between the inner wall and the outer wall of buried pipe, and complicated three-dimensional unsteady heat exchange between the outer wall of buried pipe and the filling body. In order to facilitate theoretical analysis and calculation, the following hypotheses are made for the heat release process of the filling body:

1) The filling body and horizontal buried pipe are homogeneous and isotropic solids, and the physical parameters remain constant and do not change with temperature;

2) The contact thermal resistance between filling body and buried pipe is ignored;

3) The heat transfer of filling body around buried pipe is regarded as a two-dimensional unstable solid heat conduction;

4) The influence of temperature gradient of filling body on the axial heat transfer of buried pipe is ignored;

5) The temperature and velocity of fluid are constant at the same section of infinitesimal portion of buried pipe section.

Figure 1 Physical model of heat release of filling body

Based on the analysis of theoretical and practical situation in the heat release process of filling body, there is always a moving adiabatic interface between the adjacent buried pipes. This is mainly due to the thermal imbalance between adjacent pipes when the fluid absorbs heat from filling body. Therefore, the paper will select the horizontal single U-shaped buried pipe in the non-marginal zone of filling body as research object (see Figure 2). A three-dimensional coupling heat transfer model between filling body and fluid in buried pipe is established, and the heat transfer process between fluid in horizontal U-shaped buried pipe and its surrounding filling body is numerically simulated for 12 h according to the established physical model. The aim of paper is to investigate the effect of temperature and flow characteristics of heat transfer fluid, surrounding rock temperature, buried pipe diameter and other factors on the heat release process of filling body. To make the simulation accord with reality, it is assumed that the heat storage process of filling body in the early stage has been completed, the initial temperature for heat release of filling body is equal to the end of heat storage of filling body, and it is the temperature of surrounding rock approximately. The thermo-physical parameters of heat transfer fluid, U-shaped buried pipe, and filling body are shown in Table 1.

2.2 Meshing

In this paper, Solidworks software was applied to establishing the physical model, and FLUENT simulation software was used to conduct model grid division. The grid divisions of filling body and buried pipe are shown in Figure 3. Due to the temperature change is more intense and the temperature gradient is larger in filling body of the vicinity of horizontal U-shaped buried pipe in heat release process. Therefore, the mesh is properly encrypted near the pipe wall to improve the convergence precision. At the same time, in order to minimize the numerical errors and expedite the computation and determine the optimal grid number, four sets of meshes with different cell numbers are from 2.48 million to 3.83 million. Figure 4 shows the variation diagram of the outlet temperature of heat transfer fluid and the total heat transfer of filling body after 12 h of operation for those grids. It can be seen that grid with a total cell number of 3.83 million provided the best results. It is taken for grant that internal heat source term is not taken into account and the heat transfer fluid is regarded as an incompressible fluid in this simulation study. In addition, the realizable k-ε turbulence model and the SIMPLEC computational model are adopted to improve the speed and accuracy of convergence. Finally, we consider the achievement of convergence when the energy residual value of the simulation is 10^-6 and the number of time steps is 10 s.

Figure 2 Schematic diagram of heat release for filling body:

Table 1 Thermo-physical parameters of research object

Figure 3 Computational grid for filling body and buried pipe

Figure 4 Diagram of influence parameter variation with grid number

2.3 Mathematical model

The heat release performance of filling body under the state of fluid in buried pipe extracting heat was explored by intercepting the filling body in the non-marginal zone as the research object. In order to better describe the heat exchange capacity between fluid and filling body in heat release process, their heat transfer principle will be simplified by the coupling solution of one- dimensional heat transfer model of fluid in buried pipes and heat conduction model of two- dimensional unsteady homogeneous solid of filling body outside the pipe according to the assumption in Section 2.1.

2.3.1 Heat transfer model

The horizontal single U-shaped pipes microtubule segment △Z was taken as the research object. According to the law of energy conservation, one-dimensional axial heat transfer model of fluid in buried pipes can be described as follows:

                  (1)

where T_f,_in and T_f,out are the temperatures of fluid at the inlet and outlet of microtubule segment,respectively; q is the local heat flux of microtubule segment of buried pipe; C_pf is the specific heat capacity at constant pressure of fluid in buried pipe; m_f is the mass flow rate of fluid in buried pipes.

2.3.2 Heat conduction model

The heat conduction equation of two- dimensional unsteady homogeneous solid of filling body outside the buried pipe during the heat release process can be expressed as follows:

                     (2)

where T_fb is the temperature of filling body; τ is the time of heat release process; α is the thermal diffusivity of filling body.

2.4 Initial and boundary conditions

To make the simulation conditions closer to the actual situation, we consider that the temperature of fluid in buried pipe, the temperature of tube wall, and the temperature of filling body are taken to be consistent before the heat release begins. Therefore, the initial condition of the whole heat release process of filling body is set as follows:

                    (3)

At same time, boundary conditions are set as follows:

The inlet boundary of heat transfer fluid:

                         (4)

Boundary conditions between the heat transfer fluid and the inner wall of tube:

                      (5)

The adiabatic boundary is around filling body:

                            (6)

where T_ini is the initial temperature of filling body for heat release process; λ_fb is thermal conductivity of filling body; n is the normal direction of boundary; h_f is the convection heat transfer coefficient of heat transfer fluid.

2.5 Evaluation of thermal release efficiency of filling body

In order to analyze the heat transfer efficiency between the filling body and the heat transfer fluid in buried pipe, the concept of energy efficiency coefficient E in Ref. [33] is adopted, and its calculation formula is shown as follows:

          (7)

When the inlet temperature of heat transfer fluid and the initial temperature of filling body are constant, the energy efficiency is linearly correlated with the temperature difference between the inlet and outlet of heat transfer fluid. In other words, the higher the outlet temperature, the greater the temperature difference, and the better the energy efficiency, that is to say, the higher the thermal extraction efficiency of filling body.

3 Result and discussion

3.1 Influence of initial temperature of filling body on heat release performance

The heat release performance is analyzed when the initial temperature of filling body is 35 °C, 40 °C and 45 °C respectively under the conditions that inlet velocity is 0.72 m/s and inlet temperature is 18 °C for heat transfer fluid, and the diameter of the pipe is 32 mm. Figure 5 shows the change of internal temperature for filling body with the passage of time when the initial temperature of heat release is 35 °C. It can be seen from the cloud chart analysis that the thermal influencing radius of temperature continuously diffuses to the edge with the extension of heat release time in the heat release process of filling body, but the change of thermal influencing radius will become more and more slowly. When the heat release time from 180 min to 360 min, thermal influencing radius increases from 0.19 m to 0.25 m, which is an increase of 31.57%. While thermal influencing radius increases from 0.30 m to 0.33 m from 540 min to the end of heat release (720 min), with an increase of only 10%. This is mainly because that the heat transfer temperature difference between fluid and surrounding filling body is larger at the initial stage of heat transfer and heat exchange is more obvious, but the heat exchange temperature difference between the two becomes smaller and smaller with the continuation of heat exchange, which leads to the insufficient heat release in radial distant filling body and its heat exchange effect decreases gradually.

Figure 5 Distribution of temperature field at 35 °C initial temperature of filling body:

Figure 6 shows the temperature distribution at the end of heat release process for 35 °C, 40°C and 45°C initial temperature of filling body respectively. According to the cloud chart analysis, it can be seen that when the initial temperature of filling body increases from 35°C to 45°C, at the end of heat release (720 min). Thermal influencing radius increases from 0.33 m to 0.38 m, an increase of 15.2%. Due to the increase of initial temperature of filling body, the heat transfer temperature difference between filling body and heat transfer fluid increases, and the range of thermal influencing radius around buried pipe also increases, this results in an increase in heat exchange, and the heat release effect of filling body is obvious.

Figures 7 and 8 show the influence of the initial temperature of filling body on the temperature difference between inlet and outlet of heat transfer fluid and the heat release of filling body respectively. The figures show that the temperature difference between inlet and outlet of heat transfer fluid and the heat transfer rate both increase with increasing initial temperature of filling body, and the increase decreases gradually and tends to be flat with the extension of heat release time. When the initial temperature of filling body increases from 35°C to 45°C, as shown in Figure 7, the heat is released for 20 min, the temperature difference between inlet and outlet of heat transfer fluid increases from 1.32°C to 2.04°C,increasing by 0.72°C. When the heat is released for 300 min, the temperature difference increases from 0.53°C to 0.85°C, increasing by 0.32°C. At the end of heat release (the heat is released for 720 min), the temperature difference increases from 0.44°C to 0.69°C, increasing by 0.25°C. And as shown in Figure 8, when the initial temperature of filling body increases from 35°C to 45°C, the heat is released for 20 min, the heat transfer rate of filling body increases from 623.69 W/m² to 959.86 W/m², increasing by 336.17 W/m². When the heat is released for 300 min, the heat transfer rate increases from 257.8 W/m² to 409.0 W/m², increasing by 151.2 W/m². At the end of heat release, the heat transfer rate increases from 213.6 W/m² to 339.1 W/m², increasing by 125.5 W/m².

Figure 6 Distribution of temperature field of filling body at end of heat release for different initial temperature:

Figure 7 Temperature difference at different initial temperatures of filling body

Figure 8 Heat transfer rate at different initial temperatures of filling body

According to the analysis, under the same inlet velocity and inlet temperature of heat transfer fluid, the increase of initial temperature of filling body increases the temperature difference between heat transfer fluid and filling body and enhances the heat transfer effect and the heat release of filling body. However, with the heat release process continuing, the increase of heat transfer temperature difference becomes smaller and smaller, and the heat transfer effect gradually is weakened, which leads to a decrease in outlet temperature increment of heat transfer fluid.

On the other hand, Figures 7 and 8 also show that the temperature difference between inlet and outlet of heat transfer fluid and the heat transfer rate of filling body decrease greatly with the passage of time in the early stage of heat release. With the heat release process continues, the decrease of temperature difference and heat transfer rate slows down gradually and tends to be flat. When the initial temperature of filling body is 40°C, from the heat release beginning to 220 min, the temperature difference decreases from 1.72°C to 0.74°C, decreasing by 0.98°C; the heat transfer rate of filling body decreases from 807.1 W/m² to 359.0 W/m², decreasing by 448.1 W/m². Within the interval of 500 min from 220 min to the end of heat release (720 min), the temperature difference decreases from 0.74°C to 0.57°C, only decreasing by 0.17°C; the heat transfer rate decreases from 359.0 W/m² to 276.3 W/m², only decreasing by 82.7 W/m². It indicates that the heat release is obvious in the early stage, and then tends to be slow in the later stage.

3.2 Influence of buried pipe diameter on heat release performance of filling body

The influence of buried pipe diameter (25 mm, 32 mm and 40 mm, respectively) on heat release performance of filling body is discussed when the inlet temperature of heat transfer fluid is 18 °C and the initial temperature of filling body is 40°C. Figure 9 shows the influence of pipe diameter on the temperature difference between inlet and outlet of heat transfer fluid with a certain inlet velocity (0.72 m/s) and a certain mass flow (0.58 kg/s) respectively. It indicates that at a certain inlet velocity (Figure 9(a)), the temperature difference between inlet and outlet of heat transfer fluid increases with the increase of pipe diameter; with the pipe diameter increases from 25 mm to 40 mm, the temperature difference increases from 0.89 °C to 1.23 °C when the heat is released for 60 min, and the temperature difference increases from 0.49 °C to 0.64 °C at the end of heat release (720 min). However, at a certain mass flow of heat transfer fluid (Figure 9(b)), the temperature difference between inlet and outlet of heat transfer fluid decreases with the increase of pipe diameter. With the pipe diameter increasing from 25 mm to 40 mm, the temperature difference decreases from 1.48 °C to 0.79 °C when the heat is released for 60 min, and the temperature difference decreases from 0.82 °C to 0.58 °C at the end of heat release (720 min). Data analysis shows that at a certain inlet velocity and a certain mass flow, the influence of pipe diameter on temperature difference is slightly larger at the initial stage of heat release, while the influence is weakened and tends to be flat at the later stage of heat release.

Figure 9 Influence of pipe diameter on temperature difference of heat transfer fluid at 0.72 m/s inlet velocity of heat transfer fluid (a) and 0.58 kg/s mass flow of heat transfer fluid (b)

Figure 10 shows the influence of pipe diameter on heat release of filling body with a certain inlet velocity (0.72 m/s) and a certain mass flow (0.58 kg/s) of heat transfer fluid, respectively. It indicates that the total heat transfer of filling body increases with the increase of pipe diameter in both cases. When the pipe diameter increases from 25 mm to 40 mm, the total heat transfer increases from 2.58 kW to 5.95 kW under an inlet velocity of 0.72 m/s (Figure 10(a)) and increases from 3.28 kW to 6.03 kW under a mass flow of 0.58 kg/s (Figure 10(b)) at the end of heat release (720 min). In addition, it also indicates that for any pipe diameters, the reduction of total heat transfer is obvious in the initial stage of heat release, and then the reduction gradually slows until it tends to be flat with the continuation of heat release process. For the pipe diameter of 25 mm, from the heat release 20 min to the end of heat release, the total heat transfer of filling body decreases from 6.26 kW to 2.58 kW under an inlet velocity of 0.72 m/s, and it decreases from 6.9 kW to 3.28 kW under a mass flow of 0.58 kg/s. According to the analysis, it is concluded that the temperature difference between inlet and outlet of heat transfer fluid and the total heat transfer of filling body are not only affected by the increase of heat transfer area caused by increasing pipe diameter, but also affected by the change of mass flow and inlet velocity of heat transfer fluid. At a certain velocity, the increase of pipe diameter will lead to the increase of mass flow, which makes the increase of total heat transfer of filling body not only due to temperature difference, but also due to the increase of mass flow. At a certain mass flow, with the increase of pipe diameter, the heat transfer between fluid and filling body enhances due to increasing heat exchange area; however, the decreasing velocity of heat transfer fluid weakens the heat transfer effect. Therefore, at this time, for the increase of total heat transfer of filling body, the increasing heat exchange area is the dominant factor.

Figure 10 Influence of pipe diameter on total heat transfer of filling body at 0.72 m/s inlet velocity of heat transfer fluid (a) and 0.58 kg/s mass flow of heat transfer fluid (b)

3.3 Influence of inlet velocity of fluid on heat release performance of filling body

Under conditions that the initial temperature of filling body for heat release is 40°C, the diameter of buried pipe is 32 mm, and the inlet temperature of heat transfer fluid is 18°C, the heat release performance of filling body is numerically simulated when the inlet velocity of heat transfer fluid is 0.32, 0.52, 0.72, 0.92 and 1.12 m/s, respectively. And the fluid flowing in the tube is basically in a turbulent state. The analysis by GUAN et al [33] has shown that the turbulent velocity field in the tube was more in line with the coupled heat transfer inside and outside the tube.

Figure 11 shows the variation of temperature difference between inlet and outlet of heat transfer fluid with heat release time at different inlet velocities. It indicates that the temperature difference between inlet and outlet of heat transfer fluid tends to decrease gradually with the increase of inlet velocity. When the inlet velocity increases from 0.32 m/s to 1.12 m/s, the heat is released for 300 min, the temperature difference decreases from 1.51°C to 0.44°C, decreasing by 1.07°C; at the end of heat release (720 min), the temperature difference decreases from 1.26°C to 0.37°C, decreasing by 0.89°C. The comparative analysis shows that the fluid flow in the tube is turbulent under different inlet velocities, and the increase of inlet velocity in a certain pipe diameter will lead to the increase of mass flow of heat transfer fluid. Compared with the heat transfer enhancement caused by increasing inlet velocity, the increase of mass flow becomes dominate factor affecting the outlet temperature of heat transfer fluid. The figure also shows that the temperature difference at each inlet velocity gradually decreases with the continuation of heat release process; the decrease magnitude is larger at the initial stage of heat release, and then gradually reduces and tends to be flat with the continuation of heat release process. Moreover, for the lower inlet velocity, the temperature difference has a great reduction at the initial stage of heat release process; for the inlet velocity of 0.32 m/s, the heat release time continues from 20 min to 300 min, the temperature difference decreases from 4.13°C to 1.51°C, decreasing by 2.62°C; from 300 min to the end of heat release (720 min), the temperature difference decreases from 1.51°C to 1.26°C, decreasing by 0.25°C.

Figure 11 Temperature difference between inlet and outlet of heat transfer fluid at different inlet velocities

It also can be seen that the heat transfer temperature difference between fluid and filling body decreases gradually with the extension of heat release time, which leads to the smaller and smaller increase of outlet temperature of fluid.

Figure 12 shows the comparison of heat transfer performance of filling body and heat transfer fluid for different inlet velocities at the end of heat release. For the heat release of filling body, with the increase of inlet velocity, the temperature difference between inlet and outlet of heat transfer fluid gradually decreases, while the heat transfer rate of filling body gradually increases, and they all gradually tend to be flat with the continuous increase of inlet velocity. When the inlet velocity increases from 0.32 m/s to 1.12 m/s, at the end of heat release (720 min), the heat transfer rate of filling body increases from 271.65 W/m² to 277.79 W/m², with an increase of 6.14 W/m². The result indicates that the increase of mass flow caused by increasing inlet velocity of heat transfer fluid is the dominant factor for the increase of heat transfer rate.

Figure 12 Heat transfer performance at different inlet velocities of fluid

Figure 13 shows the variation of energy efficiency coefficient with time at different inlet velocities. It can be seen that the energy efficiency coefficient decreases with increasing inlet velocity of heat transfer fluid. The energy efficiency coefficient at the inlet velocity of 0.32 m/s is significantly higher than that at the inlet velocity of 1.12 m/s at the same release time. At the end of heat release (720 min), the energy efficiency coefficient at the inlet velocity of 0.32 m/s is 0.057, while that at the inlet velocity of 1.12 m/s is 0.017, with a difference of 0.04. The analysis indicates that the energy efficiency coefficient is directly related to the temperature difference between inlet and outlet of heat transfer fluid.

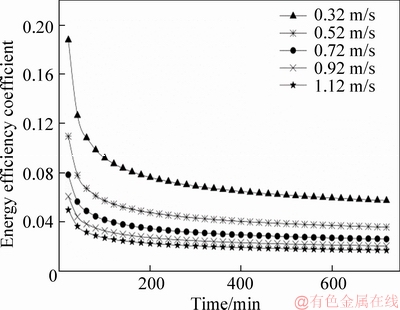
Figure 13 Energy efficiency coefficient at different inlet velocities of fluid

3.4 Influence of inlet temperature of fluid on heat release performance of filling body

Under conditions that the initial temperature of filling body for heat release is 40°C, the diameter of buried pipe is 32 mm, and the inlet velocity of heat transfer fluid is 0.72 m/s, the heat release performance of filling body is numerically simulated when the inlet temperature of heat transfer fluid is 12°C, 15°C, 18°C, 21°C and 24°C, respectively. Figure 14 shows the variation of temperature difference between inlet and outlet of heat transfer fluid with heat release time at different inlet temperatures. It indicates that with the increase of inlet temperature, the temperature difference between inlet and outlet of heat transfer fluid decreases gradually. When the inlet temperature rises from 12°C to 24°C and the heat is released for 300 min, the temperature difference decreases from 0.87°C to 0.5°C, decreasing by 0.37°C; at the end of heat release (720 min), the temperature difference decreases from 0.72°C to 0.41°C, decreasing by 0.31°C. Under any inlet temperature condition, it is also shown that the temperature difference between inlet and outlet of heat transfer fluid decreases gradually and tends to be flat with the continuation of heat release process. Moreover, for the lower inlet temperature, the temperature difference has a great reduction at the initial stage of heat release process; for the inlet temperature of 12°C, when the heat release time continues from 20 min to 300 min, the temperature difference decreases from 2.19°C to 0.88°C, decreasing by 1.31°C; from 300 min to the end of heat release (720 min), the temperature difference decreases from 0.88°C to 0.73°C, decreasing by 0.15°C.

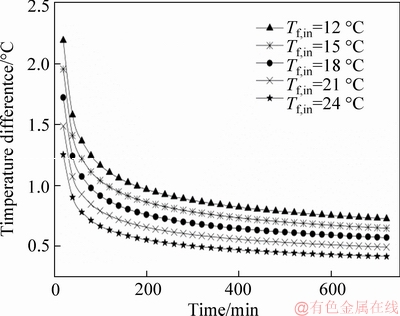
Figure 14 Temperature difference between inlet and outlet of heat transfer fluid at different inlet temperatures

Figure 15 shows that the heat release performance of filling body decreases with increasing inlet temperature of heat transfer fluid. When the inlet temperature increases from 12°C to 24°C and the heat is released for 20 min, the heat transfer rate of filling body decreases from 1027.2 W/m² to 586.9 W/m², decreasing by 440.3 W/m²; at the end of heat release (720 min), the heat transfer rate of filling body decreases from 351.7 W/m² to 200.9 W/m², decreasing by 150.8 W/m². This is mainly because the heat transfer temperature difference between heat transfer fluid in tube and filling body is lowered due to increasing inlet temperature of heat transfer fluid, it results in a decrease in heat transfer of filling body. It can be seen that appropriately lowering the inlet temperature of heat transfer fluid is conducive to the extraction of heat from filling body in heat release process of filling body, and thereby effectively relieving the problem of thermal damage in deep mine.

Figure 15 Heat transfer rate of filling body at different inlet temperatures

Figure 16 shows the variation of the total heat transfer of filling body at different inlet velocity (inlet temperature of 18°C) and inlet temperature (inlet velocity of 0.72 m/s) of heat transfer fluid at the end of heat release. It indicates that the total heat transfer of filling body increases with increasing inlet velocity, but when inlet velocity increases to a certain value, the increase of total heat transfer of filling body tends to be flat. For the inlet temperature of 18°C, when the inlet velocity increases from 0.32 m/s to 1.12 m/s, the total heat transfer of filling body increases from 5.33 kW to 5.47 kW, increasing by 0.2 kW. In addition, the total heat transfer of filling body decreases obviously with increasing inlet temperature, namely it presents a negative correlation. For the inlet velocity of 0.72 m/s, when the inlet temperature increases from 12 °C to 24°C, the total heat transfer of filling body decreases from 6.9 kW to 4.0 kW, decreasing by 2.9 kW. It can be seen that reducing inlet temperature and increasing inlet velocity of fluid can effectively increase the total heat transfer during extracting heat from filling body. But the influence of inlet temperature on the total heat transfer of filling body is significantly higher than that of the inlet velocity.

Figure 16 Total heat transfer of filling body for different inlet velocities and inlet temperatures of fluid at end of heat release

4 Conclusions

Based on the concept of synergetic exploitation of deep mineral resources and geothermal resources, heat extraction buried pipe is arranged in mine filling body, and heat transfer fluid flowing in tube is used for extracting the heat from filling body. The initial temperature of filling body, the diameter of buried pipe, the inlet temperature and inlet velocity of heat transfer fluid influencing on heat release of filling body are investigated, and the main conclusions can be drawn as fol1ows:

1) The thermal influencing radius of temperature continuously diffuses to the edge with the extension of heat release time in heat release process of filling body, but the change of thermal influencing radius will become more and more slowly. Under conditions that the initial temperature of filling body 35 °C, inlet velocity 0.72 m/s and inlet temperature 18 °C for fluid, and the pipe diameter is 32 mm, when the heat release time from 180 min to 360 min, the increase of thermal influencing radius is 31.57%; while the heat release time from 540 min to 720 min, the increase of thermal influencing radius is only 10%.

2) The higher the initial temperature of filling body, the larger the thermal influencing radius and the higher the heat transfer rate in heat release process of filling body. Under the inlet velocity of 0.72 m/s, inlet temperature of 18 °C for fluid and pipe diameter of 32 mm, when the initial temperature of filling body increases from 35°C to 45°C, the thermal influencing radius increases from 0.33 m to 0.38 m at the end of heat release, and the heat transfer rate of filling body increases by 336.17, 151.2 and 125.5 W/m², respectively at the heat release time of 20, 300 and 720 min.

3) The total heat transfer of filling body increases with increasing pipe diameter at a certain inlet velocity and a certain mass flow of fluid. Under conditions that the inlet temperature of fluid is 18 °C and the initial temperature of filling body is 40 °C, when the pipe diameter increases from 25 mm to 40 mm, the total heat transfer increases from 2.58 kW to 5.95 kW at an inlet velocity of 0.72 m/s and increases from 3.28 kW to 6.03 kW at a mass flow of 0.58 kg/s at the end of heat release.

4) With the increase of inlet velocity, the temperature difference between inlet and outlet of fluid decreases, while the heat transfer rate of filling body increases, and they all gradually tend to be flat with the continuous increase of inlet velocity. Under conditions that the initial temperature of filling body is 40 °C, the pipe diameter is 32 mm, and the inlet temperature is 18 °C, when the inlet velocity increases from 0.32 m/s to 1.12 m/s, at the end of heat release, the heat transfer rate of filling body increases from 271.65 W/m² to 277.79 W/m². The increase of mass flow caused by increasing inlet velocity is the dominant factor for the increase of heat transfer rate.

5) The heat release performance of filling body decreases with increasing inlet temperature of fluid. Under conditions that the initial temperature of filling body is 40 °C, the pipe diameter is 32 mm, and the inlet velocity is 0.72 m/s, when the inlet temperature increases from 12 °C to 24 °C, the heat is released for 20 min and the heat transfer rate decreases 440.3 W/m², at the end of heat release, the heat transfer rate decreases by 150.8 W/m².

6) Reducing inlet temperature and increasing inlet velocity of fluid can effectively increase the total heat transfer during extracting heat from filling body. But the influence of inlet temperature on the total heat transfer of filling body is significantly higher than that of the inlet velocity.

Nomenclature

T_f,in, T_f,out

Temperature of fluid at the inlet and outlet of microtubule segment respectively

△Z

Microtubule segment

q

Local heat flux of microtubule segment

C_pf

Specific heat capacity at constant pressure of fluid

m_f

Mass flow rate of fluid

T_f

Temperature of fluid

T_w

Temperature of tube wall

T_fb

Temperature of filling body

T_ini

Initial temperature of filling body for heat release process

λ_fb

Thermal conductivity of filling body

h_f

Convection heat transfer coefficient of heat transfer fluid

τ

Time of heat release process

α

Thermal diffusivity of filling body

E

Energy efficiency coefficient

References

[1] QI Chong-chong, LIU Lang, HE Jian-yong, CHEN Qiu-song, YU Li-Juan, LIU Peng-fei. Understanding cement hydration of cemented paste backfill: DFT study of water adsorption on tricalcium silicate (111) surface [J]. Minerals, 2019, 9(4): 202. DOI: https://doi.org/10.3390/min9040202.

[2] ENG Kang, LIU Zhao-peng, ZOU Quan-le, ZHANG Zhen-yu, ZHOU Jia-qi. Static and dynamic mechanical properties of granite from various burial depths [J]. Rock Mechanics and Rock Engineering, 2019. DOI: 10.1007/ s00603-019-01810-y.

[3] QI Chong-chong, FOURIE Andy, CHEN Qiu-song, LIU Peng-fei. Application of first-principles theory in ferrite phases of cemented paste backfill [J]. Minerals Engineering, 2019, 133: 47-51. DOI: 10.1016/j.mineng.2019.01.011.

[4] QIN Li-guo, FENG Xin-an, HAFEZI M, ZHANG Ya-li, GUO Jun-de, DONG Guang-neng, QIN Yuan-bin. Investigating the tribological and biological performance of covalently grafted chitosan coatings on Co–Cr–Mo alloy [J]. Tribology International, 2019, 127: 302-312. DOI: 10.1016/j.triboint.2018.06.018.

[5] MENNDEZ J, ORDEZ A, LVAREZ R, LOREDO J. Energy from closed mines: Underground energy storage and geothermal applications [J]. Renewable and Sustainable Energy Reviews, 2019, 108: 498-512. DOI: 10.1016/ j.rser.2019.04.007.

[6] GUO Ping-ye, HE Man-chao, ZHENG Lian-ge, ZHANG Na. A geothermal recycling system for cooling and heating in deep mines [J]. Applied Thermal Engineering, 2017, 116: 833-839. DOI:10.1016/j.applthermaleng.2017.01.116.

[7] NIU Yong-sheng. Research on thermal energy recycling utilization in high temperature mines [J]. Procedia Engineering, 2015, 121: 389-395. DOI: 10.1016/j.proeng. 2015.08.1083.

[8] LU Hong-jian, QI Chong-chong, CHEN Qiu-song, GAN De-qing, XUE Zhen-lin, HU Ya-jun. A new procedure for recycling waste tailings as cemented paste backfill to underground stopes and open pits [J]. Journal of Cleaner Production, 2018, 188: 601-612. DOI: 10.1016/j.jclepro. 2018.04.041.

[9] DONG Long-jun, TONG Xiao-jie, LI Xi-bing, ZHOU Jian, WANG Shao-feng, LIU Bing. Some developments and new insights of environmental problems and deep mining strategy for cleaner production in mines [J]. Journal of Cleaner Production, 2019, 210: 1562-1578. DOI: 10.1016/j.jclepro. 2018.10.291.

[10] BAO Ting, MELDRUM J, GREEN C, VITTON S, LIU Zhen, BIRD K. Geothermal energy recovery from deep flooded copper mines for heating [J]. Energy Conversion and Management, 2019, 183: 604-616. DOI: 10.1016/ j.enconman.2019.01.007.

[11] CHEN Fei, MAO Jin-feng, CHEN Shang-yuan, LI Chao-feng, HOU Pu-min, LIAO Lu. Efficiency analysis of utilizing phase change materials as grout for a vertical U-tube heat exchanger coupled ground source heat pump system [J]. Applied Thermal Engineering, 2018, 130: 698-709. DOI: 10.1016/j.applthermaleng.2017.11.062.

[12] CHEN Liu, LIU Lang, ZHANG Bo, ZHANG Xiao-yan, WANG Mei. Mechanism of backfill thermal utilization adsorption cooling system in deep mine [J]. Journal of China Coal Society, 2018, 43(2): 483-489. DOI: 10.13225/j. cnki.jccs.2017.165.(in Chinese)

[13] ZHANG Xiao-yan, JIA Yu-hang, WANG Mei, LIU Lang. Experimental research on heat transfer and strength analysis of backfill with ice grains in deep mines [J]. Sustainability 2019, 11(9): 2486. DOI: 10.3390/su11092486.

[14] WANG Mei, LIU Lang, CHEN Liu, ZHANG Xiao-yan, ZHANG Bo, JI Chang-fa. Cold load and storage (CLS) functional backfill for cooling deep mine [J]. Advances in Civil Engineering, 2018. DOI: 10.1155/2018/5435214.

[15] ZHANG Ya-ping, WANG Mei, HAO Gai-hong. Thermomechanical analysis of system used to cooling and dehumidity in mine [J]. Journal of China Coal Society, 2016, 35(10): 146-148. DOI: 10.13301/j.cnki.ct.2016.10.057. (in Chinese)

[16] HUAN Chao, WANG Feng-hao, LI Sheng-teng, ZHAO Yu-jiao, LIU Lang, WANG Zhi-hua, JI Chang-fa. A performance comparison of serial and parallel solar-assisted heat pump heating systems in Xi’an, China [J]. Energy Science & Engineering, 2019: 1-15. DOI: 10.1002/ese3.357.

[17] GHOREISHI-MADISEH S A, HASSANI F, ABBASY F. Numerical and experimental study of geothermal heat extraction from backfilled mine stopes [J]. Applied Thermal Engineering, 2015, 90: 1119-1130. DOI: 10.1016/ j.Applthermaleng. 2014.11.023.

[18] LAMARCHE L. Horizontal ground heat exchangers modelling [J]. Applied Thermal Engineering, 2019, 55: 534-545. DOI: 10.1016/j.Applthermaleng.2019.04.006.

[19] KERME E D, FUND A S. Heat transfer simulation analysis and performance study of single U-tube borehole heat exchanger [J]. Renewable Energy, 2020, 145: 1430-1448. DOI: 10.1016/j.renene.2019.06.004.

[20] KONG Xiang-ri, DENG Ye-lin, LI Lin-yan, GONG Wei-shen, CAO Shi-jie. Experimental and numerical study on the thermal performance of ground source heat pump with a set of designed buried pipes [J]. Applied Thermal Engineering, 2017, 114: 110-117. DOI: 10.1016/ j.applthermaleng.2016.11.176.

[21] KAYACI N, DEMIR H. Numerical modelling of transient soil temperature distribution for horizontal ground heat exchanger of ground source heat pump [J]. Geothermics, 2017, 73: 33-47. DOI: 10.1016/j.geothermics.2018.01.009.

[22] AL-AMEEN Y, LIANAKIEV A, EVANS R. Recycling construction and industrial landfill waste material for backfill in horizontal ground heat exchanger systems [J]. Energy, 2018, 151: 556-568. DOI: 10.1016/j.energy.2018.03.095.

[23] JI Guang-hui HUANG Guang-qin. Impact of load distribution on ground heat exchanger under thermal equilibrium between heat extraction and heat release [J]. Building Science, 2017, 33(10): 104-112. DOI: 10.13614/ j.cnki.11-1962/tu.2017.10.16. (in Chinese)

[24] YANG Wei-bo, KONG Lei, YIN Yan-shan. Numerical simulation and experimental validation on heat exchange characteristics of horizontal slinky soil ground heat exchanger [J]. Fluid Machinery, 2018, 46(6): 60-67. DOI: 10.3969/j.issn.1005-0329.2018.06.013.(in Chinese)

[25] CHEN Jin-hua, XIA Lei, LI Bai-zhan, MMEREKI D. Simulation and experimental analysis of optimal buried depth of the vertical U-tube ground heat exchanger for a ground-coupled heat pump system [J]. Renewable Energy, 2015, 73: 46-54. DOI: 10.1016/j.renene.2014.06.007.

[26] ZHOU Tong. Experimental study on heat transfer performance of buried pipe heat exchanger with twisted tape inserts in the backfill materials of sand/graphite [D]. Beijing: Beijing Jiaotong University, 2018. (in Chinese)

[27] LI Chao, GUAN Yan-ling, YANG Rui-tao, LU Xiong, XIONG Wen-xue, LONG An-jie. Effect of inner pipe type on the heat transfer performance of deep-buried coaxial double-pipe heat exchangers [J]. Renewable Energy, 2020, 145:　1049-1060.　DOI:　10.1016/j.renene.2019.06.101.

[28] LV Yi-qing, FU Yun-zhun, CAI Yin-ling. Numerical simulation and experimental study of heat release performance of multi-port u-type buried pipes [J].　Acta　Energiae Solaris Sinica, 2016, 37(12): 3110-3116. (in Chinese)

[29] LIU Lang, ZHU Chao, QI Chong-chong, ZHANG Bo, SONG Ki-il. A microstructural hydration model for cemented paste backfill considering internal sulfate attacks [J]. Construction and Building Materials, 2019, 211: 99-108.　DOI: 10.1016/j.conbuildmat.2019.03.222.

[30] LIU Lang, YANG Pan, QI Chong-chong, ZHANG Bo, GUO Li-jie, SONG Ki-il. An experimental study on the early-age hydration kinetics of cemented paste backfill [J]. Construction and Building Materials, 2019, 212: 283-294.　DOI: 10.1016/j.conbuildmat.2019.03.322.

[31] GUO Li-jie, YU Bin. Status and future of filling technology and equipment in metal mines in China [J]. Mining Technology, 2011, 1(3): 12-14, 37.　DOI:　10.3969/j.issn.　1671-2900.2011.03.004.

[32] WANG Li-hong, BAO Ai-hua, LUO Yuan-yuan. Development and outlook on the filling method in China [J]. Mining Research and Development, 2017, 37(3): 1-7. DOI: 10.13827/J.cnki.kyyk.2017.03.001. (in Chinese)

[33] GUAN Yan-ling, ZHAO Xiao-li, WANG Guan-jun, DAI Jun, ZHANG Hao. 3D dynamic numerical programming and calculation of vertical buried tube heat exchanger performance of ground-source heat pumps under coupled heat transfer inside and outside of tube [J]. Energy and Buildings, 2017, 139: 186-196. DOI: 10.1016/j.enbuild. 2017.01.023.

(Edited by YANG Hua)

中文导读

埋管内流体采热状态下充填体释热性能的数值模拟

摘要：在矿山充填体内布置采热埋管，是矿床-地热协同开采技术的基本要求，而充填体的释热性能直接影响地热的采出效率。本文基于换热基本理论，利用FLUENT模拟软件建立充填体释热过程的三维非稳态换热模型，并以水平U型采热埋管为研究对象，分析充填体释热过程中采热埋管周围充填体温度场的变化规律，探讨充填体初始温度、采热埋管管径、管内采热流体的入口流速、入口温度对其轴向一定距离内采热流体与周围充填体两区域之间耦合传热，以及对采热流体进出口温差、充填体释热性能的影响，不仅为实现深部矿山矿产资源与地热协同开采奠定理论基础，而且也为充填体内采热埋管的布置、采热流体的工况选择提供参考依据。

关键词：充填体；埋管；换热流体；释热性能

Foundation item: Projects(51974225, 51874229, 51674188, 51904224, 51904225, 51504182) supported by the National Natural Science Foundation of China; Projects(2018JM5161, 2018JQ5183, 2015JQ5187) supported by the Natural Science Basic Research Plan of Shaanxi, China

Received date: 2019-05-31; Accepted date: 2019-07-23

Corresponding author: LIU Lang, PhD, Professor; Tel: +86-29-85583143; E-mail: liulang@xust.edu.cn; ORCID: 0000-0001-9536-0508