Alloying effects of V on stability, elastic and electronic properties of TiFe2 via first-principles calculations
来源期刊:中南大学学报(英文版)2017年第7期
论文作者:农智升 崔普昌 朱景川 赵荣达
文章页码:1551 - 1559
Key words:first-principles; elastic properties; alloying effect; TiFe2 phase
Abstract: The alloying effects of V on structural, elastic and electronic properties of TiFe2 phase were investigated by the first-principles calculations based on the density functional theory. The calculated energy properties including cohesive energy and formation enthalpy indicate V atom would preferentially substitute on 6h sites of Fe atoms in the lattice of TiFe2 to form the intermetallic Ti4Fe7(V). The calculated results of polycrystalline elastic parameters confirm that the plasticity of TiFe2 would be improved with the addition of V. By discussing the percentage of elastic anisotropy, anisotropy in linear bulk modulus and directional dependence of elastic modulus, it is revealed that the anisotropy of TiFe2 and Ti4Fe7(V) is small. Finally, the density of states, charge density distribution and Mulliken population for TiFe2 and Ti4Fe7(V) were calculated, suggesting there is a mixed bonding with metallic, covalent and ionic nature in TiFe2 and Ti4Fe7(V) compounds. These results also clarify that the reason for the improvement of plasticity with the addition of V in TiFe2 is the weakened bonding of covalent feature between Ti and V atoms.
Cite this article as: NONG Zhi-sheng, CUI Pu-chang, ZHU Jing-chuan, ZHAO Rong-da. Alloying effects of V on stability, elastic and electronic properties of TiFe2 via first-principles calculations [J]. Journal of Central South University, 2017, 24(7): 1551-1559. DOI: 10.1007/s11771-017-3560-3.
J. Cent. South Univ. (2017) 24: 1551-1559
DOI: 10.1007/s11771-017-3560-3
NONG Zhi-sheng(农智升)1, CUI Pu-chang(崔普昌)1, ZHU Jing-chuan(朱景川)2, ZHAO Rong-da(赵荣达)3
1. School of Materials Science and Engineering, Shenyang Aerospace University, Shenyang 110136, China;
2. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China;
 Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Central South University Press and Springer-Verlag Berlin Heidelberg 2017
Abstract: The alloying effects of V on structural, elastic and electronic properties of TiFe2 phase were investigated by the first-principles calculations based on the density functional theory. The calculated energy properties including cohesive energy and formation enthalpy indicate V atom would preferentially substitute on 6h sites of Fe atoms in the lattice of TiFe2 to form the intermetallic Ti4Fe7(V). The calculated results of polycrystalline elastic parameters confirm that the plasticity of TiFe2 would be improved with the addition of V. By discussing the percentage of elastic anisotropy, anisotropy in linear bulk modulus and directional dependence of elastic modulus, it is revealed that the anisotropy of TiFe2 and Ti4Fe7(V) is small. Finally, the density of states, charge density distribution and Mulliken population for TiFe2 and Ti4Fe7(V) were calculated, suggesting there is a mixed bonding with metallic, covalent and ionic nature in TiFe2 and Ti4Fe7(V) compounds. These results also clarify that the reason for the improvement of plasticity with the addition of V in TiFe2 is the weakened bonding of covalent feature between Ti and V atoms.
Key words: first-principles; elastic properties; alloying effect; TiFe2 phase
1 Introduction
Nowadays there are more and more Laves phases with AB2 structure being applied in aerospace structure materials, heat resisting materials and hydrogen storage materials, which is due to their excellent structural stability and designability[1-5]. The intermetallic compound TiFe2, which meets the stability range of atomic ratio for the C14 structure, has caught widely attention because its structural degrees of freedom can effectively combine with the magnetic degrees of freedom. Hence, the study on magnetic measurements of the hexagonal TiFe2 Laves phase (Cl4 structure) has been increased. Based on the lattice constants of TiFe2, the magnetic ground state energy was investigated by HOFFMANN et al [6] using first-principles calculations. It was found that as the antiferromagnetic (AF) state is slightly favored, TiFe2 shows continually subdued AF and ferromagnetic (FM) ground states.
Although TiFe2 phase has attractive and potential magnetic applications, its room temperature brittleness enormously limits its development. It is well known that alloying is an effective method to improve the mechanical properties of alloys by changing elastic constants of alloys. The elastic constants of materials play an important role in deciding the reaction of the crystal resisting the external stress, and are necessary parameters for determining the mechanical properties of solid materials [7]. The experimental results have revealed that the addition of V plays a very important role in optimizing the microstructures and mechanical properties of C14 TiX2 (X=Cr, Ti and Mn) alloys [8]. However, there is little theoretical investigation on the elastic and electronic properties of TiFe2 phase, and the study of alloying with V in TiFe2 phase at the atomic and electronic level is not sufficient. Moreover, the effect of V atom on the plasticity, especially the mechanisms of the interaction between TiFe2 and V atom are not clear.
In this work, the stability, elastic constants and electronic structure of TiFe2 alloyed with V atom were obtained by the first-principles calculations. The elastic anisotropy, bonding behavior and interaction between atoms were discussed in detail.
2 Calculation method
For theoretically analyzing the influence of V atom on structure and energy of TiFe2, the density functional theory (DFT) with ultrasoft pseudo-potentials [9] was carried out in the cambridge sequential total energy package (CASTEP) code. In this code, first-principles quantum mechanics calculations were operated by the plane-wave pseudo-potential. The generalized gradient approximation (GGA) of the Perdew-Wang 91 version (PW91) [10, 11] was adopted as the exchange and correlation terms. The cutoff energies of 350 eV were set for all calculations to ensure the precision. The convergence conditions of these calculations can be described as: the maximum force, maximum displacement, maximum stress and energy change were below 0.01 eV/ , 5.0×10-4
, 5.0×10-4  , 0.02 GPa and 5.0×10-6 eV/atom, respectively.
, 0.02 GPa and 5.0×10-6 eV/atom, respectively.
TiFe2 phase crystallizes in C14 structure with symmetry of P63/mmc (No. 194) and contains 12 atoms per unit cell. In this unit cell, 4 Ti atoms are located on 4f sites and 8 Fe atoms on 2a and 6h sites. The Fe (6h) sites take effective magnetic moments, but there are any molecular fields in the Fe (2a) sites due to structural symmetry [12-14]. The direction of the magnetic moments for Fe (6h) sites is along the c-axis, as shown in Fig. 1. The structures, in which the alloying atom V is placed at Fe (2a) and (6h) sites, substituting for Fe atoms, are named as Ti4Fe7(V)-1 and Ti4Fe7(V)-2, respectively. In addition, the alloying atom V is placed at Ti (4f) site, which is Ti3(V)Fe8.

Fig. 1 Crystal structure of Laves phase TiFe2 (Arrows represent direction of magnetic moments for Fe atoms)
3 Results and discussion
3.1 Structure and stability of TiFe2 alloyed with V
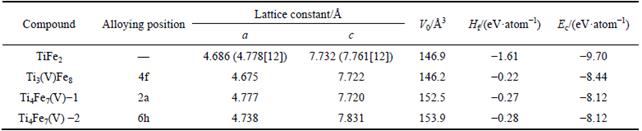
The optimized crystal structures of TiFe2, Ti4Fe7(V)-1, Ti4Fe7(V)-2 and Ti3(V)Fe8 are obtained by using the Broyden-Fletcher-Goldfarb-Shanno (BFGS) methods [15], and then the equilibrium lattice constants can also be calculated. Table 1 shows the calculated results of equilibrium structural parameters for TiFe2, Ti4Fe7(V)-1, Ti4Fe7(V)-2 and Ti3(V)Fe8 at zero pressure, where V0 is the volume of unit cell, Ec is the cohesive energy and Hf is the formation enthalpy. Although there are lack of experimental lattice constants for TiFe2 alloyed with V, the consistent values between calculated and experimental lattice constants of TiFe2 measured by WERTHEIM et al [12] (a=b=4.778  and c=7.761
and c=7.761 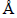 ) indicate that the precision for these calculations meets the requirements of analysis. In addition, there is an obvious increase of cell volumes (or lattice distortion) when Fe atom was substituted by V atom in the crystal structure of TiFe2, which results mainly from the V atom with larger atomic radius (1.71
) indicate that the precision for these calculations meets the requirements of analysis. In addition, there is an obvious increase of cell volumes (or lattice distortion) when Fe atom was substituted by V atom in the crystal structure of TiFe2, which results mainly from the V atom with larger atomic radius (1.71 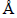 ) occupying the position of Fe atom with lesser atomic radius (1.56
) occupying the position of Fe atom with lesser atomic radius (1.56 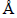 ).
).
For further investigating the structural stability of TiFe2, Ti4Fe7(V)-1, Ti4Fe7(V)-2 and Ti3(V)Fe8 from the view of energy, the formation enthalpy Hf and cohesive energy Ec are introduced to discuss the influence of different substitution positions of V atom on the structural stability of TiFe2. Hf and Ec are usually used to describe the alloying ability and structural stability of a compound, respectively. Hf is defined as the energy difference that the total energy of final compound subtracts that of initial constituents in proportion [16], and can be expressed by Eq. (1). Similarly, Ec is the energy to decompose the crystal structure of initial compound into free atoms by the ratio of chemical formula [17], and can be calculated by Eq. (2):
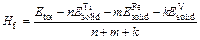 (1)
(1)
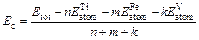 (2)
(2)
Table 1 Calculated and experimental results equilibrium structural parameters
where Etot is the calculated total energy of TiFe2, Ti4Fe7(V)-1, Ti4Fe7(V)-2 or Ti3(V)Fe8, n, m and k are atom numbers of Ti, Fe and V in these compounds, respectively. 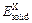 and
and 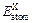 (X=Ti, Fe and V) are the energy per X element in corresponding initial stability states and under each isolated states, respectively. The energy of isolated state for an atom is obtained by calculating the crystal total energy of corresponding elements in a large box.
(X=Ti, Fe and V) are the energy per X element in corresponding initial stability states and under each isolated states, respectively. The energy of isolated state for an atom is obtained by calculating the crystal total energy of corresponding elements in a large box.
The calculated formation enthalpy Hf and cohesive energy Ec for TiFe2 and TiFe2 alloyed with V listed in Table 1 show that TiFe2, Ti4Fe7(V)-1, Ti4Fe7(V)-2 and Ti3(V)Fe8 all have stable crystal structures due to their lower cohesive energies. It can be easily seen that TiFe2 has the lowest value of formation enthalpy and cohesive energy, suggesting that the alloying ability and structural stability of TiFe2 all obviously weaken with the addition of V in the crystal structure of TiFe2. The reason for this result is probably that the magnetic symmetry of TiFe2 compound is broken with the addition of V, and the magnetic disorder would increase the energy of structure resulting in the decline of alloying ability and structural stability. Moreover, it should be noted that the structures in which the alloying atom V substitutes for the Fe atom in the structure of TiFe2 present a lower value of formation enthalpy than that of Ti3(V)Fe8, which indicates that V atom would substitute on the 6h sites of Fe atoms in the lattice of TiFe2 easily, to form the intermetallic Ti4Fe7(V)-2.
3.2 Elastic properties of TiFe2 alloyed with V
The elastic constants (Cij) of a compound reflect the ability of the crystal resisting the applied stress, and the change of Cij is important for investigating the influence of V atom on the plasticity of TiFe2. In this calculation section, the elastic constants are estimated by the method of calculating the fluctuations of total energy of a crystal under different small strains to the equilibrium structure. The elastic strain energy can be calculated by [18]
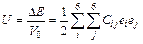 (3)
(3)
where ΔΕ is the total energy of deformed structure minus that of initial one, V0 is the volume of structure at the equilibrium state, Cij represents the elastic constants, and ei and ej are applied strains. For TiFe2 with hexagonal structure, there are five independent elastic constants, and Table 2 lists the corresponding five types of strains for the hexagonal structure [19]. In Table 2, 5 different strain types have corresponding applied strains parameters represented by using δ, and the unlisted strains are all zero. Based on Eq. (3), types of elastic constants Cij are also obtained when ΔE/V0 is equal to 0. In order to obtain the fluctuations of total energy for a hexagonal structure, five appropriate deformations according with each type of strains listed in Table 2 are employed. The calculated elastic constants of TiFe2 and TiFe2 alloyed with V are listed in Table 3. The values of C11 and C33 reflect the ability that structure resists external uniaxial compression along the x and z axes, respectively. The larger the value is, the better the ability of resistance is. It can be easily seen that Ti3(V)Fe8 and TiFe2 show a larger values of C11 and C33, while there is an obvious decrease of C11 or C33 when alloying atom V substitutes for the Fe atom in the structure of TiFe2. It suggests that comparing with TiFe2, the ability of resistance to be uniaxial compressed would weaken when Fe atom is replaced by V atom in the crystal.
Table 2 Strains used to calculate elastic constants of TiFe2 with hexagonal structure

The mechanical stability of a compound is associated with the elastic constants, and the Born stability criteria [20] can be an effective measure to judge whether the structure is stable or not from the values of Cij. The Born stability criteria for a hexagonal structure at zero pressure is given by
C12>0, C44>0, C11-C12>0, 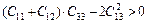 (4)
(4)
From Table 3, the calculated values of elastic constants for TiFe2 and TiFe2 alloyed with V satisfy well the stability criteria. It indicates that these compounds are all with mechanical stable structure at zero pressure.
Table 3 Elastic constants Cij of TiFe2 and TiFe2 alloyed with V

Based on calculated values of Cij, bulk modulus (B), shear modulus (G), Young’s modulus (E) and Poisson ratio (ν), these polycrystalline mechanical properties for TiFe2 and TiFe2 alloyed with V can be easily obtained by using the Voigte-Reusse-Hill (V-R-H) approximations [21], and the computational formulas are listed as follows:

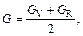

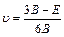 (5)
(5)
where subscripts V and R express the model of Voigt and Reuss, respectively.
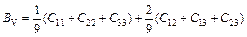 ;
;
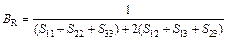 ;
;
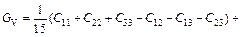
 ;
;
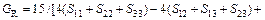
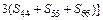 (6)
(6)
The elastic properties for polycrystalline hexagonal TiFe2 and TiFe2 alloyed with V are calculated and listed in Table 4. The B and G reflect the ability that structure resists volume change under external compression and reversible deformations in the direction of shear stress, respectively [22]. The present calculated results indicate that TiFe2 displays larger B and G than Ti4Fe7(V)-1, Ti4Fe7(V)-2 and Ti3(V)Fe8, suggesting that the resistance to volume change and reversible deformations all weaken as V atom enters into the crystal structure of TiFe2. Furthermore, B and G show the lowest values when V atom substitutes on the 6h sites of Fe atoms in the lattice of TiFe2. In addition, the larger E corresponds to the stiffer material. The calculated results indicate that TiFe2 is much stiffer than the others, and there is a similar change rule between E and B in TiFe2 and TiFe2 alloyed with V compounds.
The plasticity of materials plays an important role in industry application, and is usually evaluated by the Poisson ratio ν. The bigger value of ν corresponds to the better plasticity of materials. It can be seen from Table 5 that comparing with TiFe2, the compound that V atom substitutes on the 6h sites of Fe atoms in the lattice of TiFe2 shows a higher Poisson ratio of 0.31. Based on the results of formation enthalpy, V atom would substitute on the 6h sites of Fe atoms in the lattice of TiFe2 easily, to form the intermetallic Ti4Fe7(V)-2. It is clear that the addition of V atom within the TiFe2 lattice can indeed improve the plasticity of TiFe2 alloy. Moreover, according to Pugh’s assumption, the ratio of bulk to shear modulus B/G is an effective parameter to predict brittle or ductile behavior of materials [22]. When B/G> 1.75 is satisfied, the bigger value of B/G is, the better the plasticity is. In the present work, the calculated value of B/G for Ti4Fe7(V)-2 is 2.23, which is higher than that of TiFe2 (B/G=2.06), implying that the compound that V atom substitutes on the 6h sites of Fe atoms in the lattice of TiFe2 is more ductile than TiFe2. These results are also in agreement with the conclusions of Poisson ratio discussed above.
Consequently, in the present work, taking the obtained formation enthalpy and elastic properties of TiFe2 and TiFe2 alloyed with V into consideration, the structure of Ti4Fe7(V)-2, in which V atom substitutes on the 6h sites of Fe atoms in the lattice of TiFe2, is chosen for further investigation on the elastic anisotropy and electronic properties, and is named as Ti4Fe7(V).
3.3 Elastic anisotropy of TiFe2 alloyed with V
The microcracks of materials, which are closely related to the elastic anisotropy of crystals, are an important facet to evaluate the application of materials in engineering [23]. The elastic anisotropy including the compressibility anisotropy (AB) and shear anisotropy (AG) are widely used to investigate the elastic anisotropy, and can be calculated as [24]:
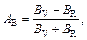
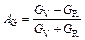 (7)
(7)
where B and G refer to bulk and shear modulus, respectively. When the values of AB and AG are 100%, it means that the structure is maximum anisotropic, while 0 suggests that the isotropy of structure shows the feature of isotropy. As shown in Table 5, TiFe2 and Ti4Fe7(V) all display small anisotropy in shear and compression. TiFe2 is more isotropic in compression, while Ti4Fe7(V) is more isotropic in shear.
Table 4 Elastic modulus for TiFe2 and TiFe2 alloyed with V by using V-R-H approximations
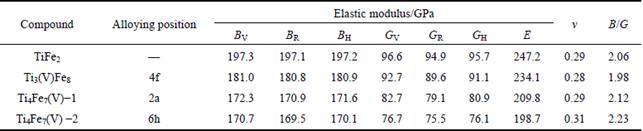
Table 5 Elastic anisotropy AB, AG and anisotropy in linear bulk modulus of TiFe2 and Ti4Fe7(V)

For a hexagonal structure, there is another effective method to express the elastic anisotropy, and it is the anisotropy in linear bulk modulus. Ba and Bc are the linear bulk modulus along the a-axis and c-axis, respectively, and can be taken as [25]:
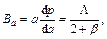
 (8)
(8)
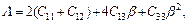
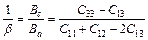 (9)
(9)
where β reflects the influence of deformation function for a-axis on the c-axis, thus, 1/β means the anisotropy in linear bulk modulus along the c-axis regarding the a-axis. If the value of Bc/Ba is closer to 1, it implies the better isotropic compressibility of materials. Table 5 shows the calculated values of Ba and Bc for TiFe2 and Ti4Fe7(V). It can be easily seen that the anisotropy in linear bulk modulus of TiFe2 is smaller than that of Ti4Fe7(V) because the ratio of Bc/Ba for TiFe2 is closer to unity, which is consistent with the conclusion of the elastic anisotropy for bulk modulus AB.
Besides above AB, AG and Bc/Ba which are three dimensionless quantities, another significant method of describing elastic anisotropy is the directional dependence of E, which is the three-dimensional surface representation and can be used to describe the in-plane elastic anisotropy. The directional dependence of E for a hexagonal symmetry crystal can be calculated by [26]
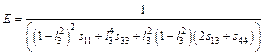 (10)
(10)
where l3 is the direction cosine to the c axis, and Sij are the elastic compliance constants. Based on the calculated elastic compliance constants and direction cosine, the directional dependence of E for TiFe2 and Ti4Fe7(V) can be obtained by Eq. (10), as shown in Fig. 2. The spherical shape of the three-dimensional surface representation for the directional dependence of E implies a fully isotropic system of crystal. It is clearly seen that the obvious non-spherical nature of elastic modulus for TiFe2 and Ti4Fe7(V) shown in Fig. 2 indicates the anisotropy in the plane, which is consistent with the above results on the percentage elastic anisotropy. In addition, This in-plane elastic anisotropy of TiFe2 and Ti4Fe7(V) can be further understood by the interaction between atoms, and also the feature of chemical bonding, which would be investigated in the section of electronic structure.
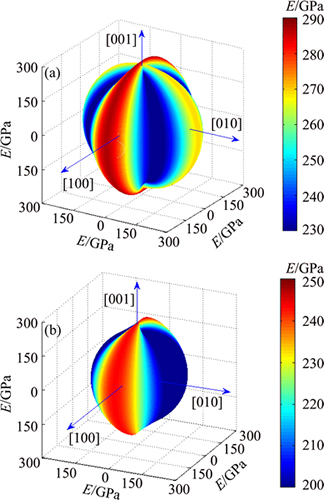
Fig. 2 Calculated directional dependence of elastic modulus E for TiFe2 (a) and Ti4Fe7(V) (b) compounds
3.4 Electronic structure of TiFe2 alloyed with V
The density of states, which is associated with the bonding interaction within compounds, is usually employed to reveal the structural stability and elastic properties. In this section, the total density of states (TDOS) and partial density of states (PDOS) at equilibrium structures for TiFe2 and Ti4Fe7(V) are calculated and presented in Fig. 3. The TDOS of TiFe2 and Ti4Fe7(V) are all mainly constituted by p and d states of Ti and Fe (and V element for Ti4Fe7(V)) elements, and the s states of these elements also have some contributions at lower energy level. These compounds all form metallic bonding due to the positive values of TDOS for TiFe2 and Ti4Fe7(V) at the Fermi level. For the antiferromagnetic TiFe2, as shown in Fig. 3(a), it can be seen that spin-up and down states have the same TDOS while there is difference of direction between these spin-up and down states. The reason can be attributed to the symmetric magnetic structure of TiFe2, because only Fe (6h) sites carry an effective and symmetric magnetic moment (shown in Fig. 1) in TiFe2 compound [12-14]. Regarding Ti4Fe7(V), owing to the alloying atom V replacing the 6h sites of Fe atoms in the lattice of TiFe2, the symmetry of structure is broken, resulting in the broken symmetry of the spin-up and down TDOS for Ti4Fe7(V), as shown in Fig. 3(b). Hence, Ti4Fe7(V) presents an obvious ferromagnetic characteristic. The origin of magnetism as well as hybridization process for TiFe2 and Ti4Fe7(V) can also be revealed by analyzing the feature of PDOS. Figure 3(a) shows that the d-d hybridizations between Ti and Fe atoms in the energy range from about -4 to -2 eV and 0 to 2 eV are clear, and the Fe-p states also play a role in the hybridization within the range of -2 to 2 eV. These d-d hybridizations, which are the common character in the hexagonal structure, imply that some covalent interaction exists between Fe and Ti atoms in TiFe2 compound [27]. Hence, the TiFe2 presents a pronounced structural stability. Comparing with TiFe2, there are four notable peaks at about -3.5, -1.7, 0.3 and 1.2 eV in the up-spin PDOS of Ti4Fe7(V). In particular, the peaks at -3.5 eV and 0.3 eV have strong hybridizations between Fe-d, Ti-d and V-d. In addition, the down-spin PDOS of Ti4Fe7(V) has four peaks located at about -3.8, -2.8, -0.9 and 0.9 eV, and only the peak at -2.8 eV has stronger hybridization between the down-spin electrons of Fe-d and V-d. The different orbital hybridizations between the spin-up and spin-down TDOS in Ti4Fe7(V) which can lead to the charge transfer between different elements are an important reason for bringing the ferromagnetic characteristic of Ti4Fe7(V).
Besides density of states, the charge density distribution can also reveal the feature of bonding from the view of electron density. Figure 4 shows the charge density distributions maps on (0 1 -1 0) plane for TiFe2 and Ti4Fe7(V). The core electron distributions of Fe, Ti and V atoms, which are visualized in the form of higher density regions, usually contribute little to the bonding. Moreover, there is obvious metallic bonding between these metal atoms forming in TiFe2 and Ti4Fe7(V) due to the appearance of the delocalized valence electron clouds in these charge density distributions maps. It also can be seen that the shapes of metal atoms including Fe, Ti and V atoms are slightly deformed, and obvious overlaps of electron densities are found between Fe1 and Fe2 atoms, which indicates that there is covalent bonding forming between the nearest Fe atoms. In addition, in contrast to the covalent bonding of Fe1-Fe2, obvious high density regions, which are found between Fe (or V shown in Fig. 4(b)) and its nearest Ti atoms, are firmly localized around these Fe (or V) atoms. Obviously, the Fe-Ti and V-Ti bonding in these compounds are confirmed to be with covalent and somewhat ionic feature [28].
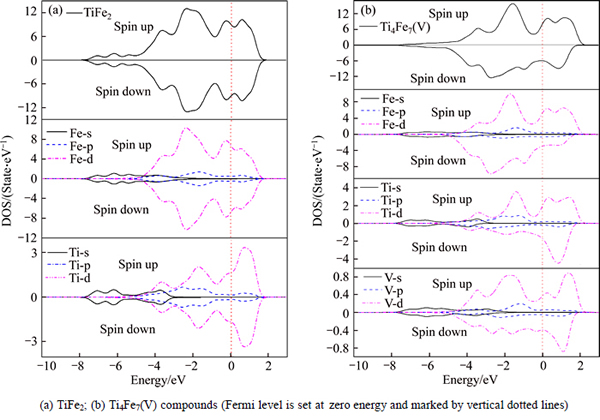
Fig. 3 Total density of states (TDOS) and partial density of states (PDOS)
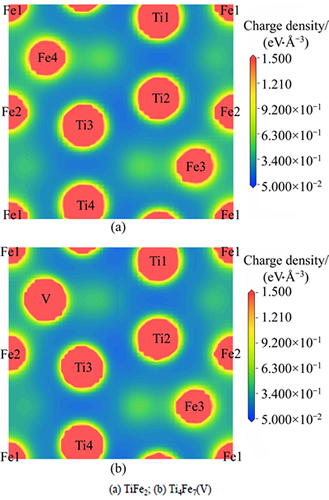
Fig. 4 Charge density distribution maps on  plane
plane
Consequently, there is a mixed bonding of metallic, covalent and ionic nature in TiFe2 and Ti4Fe7(V) compounds. It is the main reason for the high strength and stability, and also a common feature for the electronic structure of C14 AB2 type Laves phases [18]. In particular, it can be seen from Fig. 4(b) that the density of charge localization around V atom is obviously lower than that around Fe3 atom, and this V atom exactly is the atom that replaces on the 6h sites of Fe atoms in the lattice of TiFe2 to form the Ti4Fe7(V), suggesting that comparing with TiFe2, the formation of V-Ti bonding in Ti4Fe7(V) makes the ionic and covalent interaction weak. Generally speaking, a stronger bonding directionality is a disadvantage for ductility in a compound [29, 30]. Therefore, the ductility of TiFe2 may be less than that of Ti4Fe7(V), which agrees with the results of elastic properties. The addition of V in TiFe2 can indeed increase the plasticity by weakening the bonding interaction between Ti and alloying atoms V.
As a necessary complementary to the charge density distributions maps, the atomic Mulliken populations are widely used to analyze the bonding behavior from the view of the change of charge distribution on atoms. The atomic Mulliken population on  plane for TiFe2 and Ti4Fe7(V) are calculated, and the results are listed in Table 6. Valence states of these atoms in this calculation are Ti 3s23p63d24s2, Fe 3d64s2 and V 3s23p63d34s2.
plane for TiFe2 and Ti4Fe7(V) are calculated, and the results are listed in Table 6. Valence states of these atoms in this calculation are Ti 3s23p63d24s2, Fe 3d64s2 and V 3s23p63d34s2.
Table 6 Atomic Mulliken population on  plane for TiFe2 and Ti4Fe7(V) (Ions represent different positions of atoms shown in Fig. 4)
plane for TiFe2 and Ti4Fe7(V) (Ions represent different positions of atoms shown in Fig. 4)
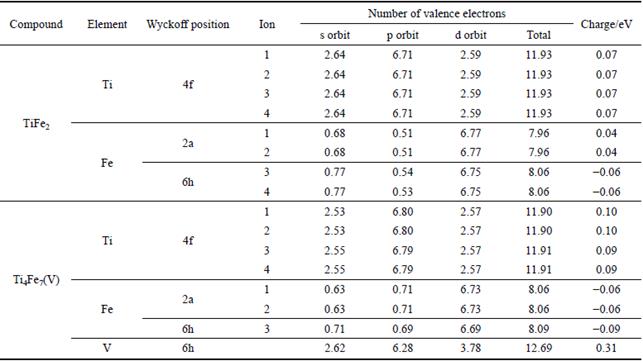
The integrated charge intensities of Ti atoms in TiFe2 and Ti4Fe7(V) are all positive, suggesting that Ti atoms all lose electron, and there is charge transferring from Ti to other atoms. Parts of Ti-4s states are the main orbit of losing valence electrons in these compounds, and these electrons partly transfer to 3p and 3d states of Ti atoms as the incremental free-electron, while the others contribute to other atoms after bonding. Regarding TiFe2 compounds, the change of charge distribution on Fe atoms which are on 2a sites has the same rule with the Ti atoms, while Fe atoms on 6h sites obtain these lost electron and show negative charge. In contrast to TiFe2 compound, Fe atoms in Ti4Fe7(V) all obtain electron because there is a large number of charge transferring from V atom to other atoms. Obviously, the bonding of ionic feature slightly strengthens while the bonding of covalent feature weakens with the addition of V atom in TiFe2. It is the main source of the improvement of plasticity for TiFe2, and consistent with the results of charge density distribution. By the way, it should be noted that the sum of charge for all atoms in Table 6 is not equal to 0, because these atoms are only on the  plane of TiFe2 (or Ti4Fe7(V)), not all the atoms in TiFe2 (or Ti4Fe7(V)) compound.
plane of TiFe2 (or Ti4Fe7(V)), not all the atoms in TiFe2 (or Ti4Fe7(V)) compound.
4 Conclusions
The first-principles calculations based on DFT about the addition of V on C14 TiFe2 compound have been performed. The consistent values between calculated equilibrium lattice constants and experimental ones of TiFe2 confirm the precision of calculations. These compounds all present better structural stability due to their lower Ec. The results of formation enthalpy show that V atom would preferentially substitute on the 6h sites of Fe atoms in the lattice of TiFe2, to form the intermetallic Ti4Fe7(V). The calculated results of polycrystalline elastic parameters show that the addition of V atom within the TiFe2 lattice can indeed improve the plasticity of TiFe2 alloy. Based on the calculated results of electronic structure for TiFe2 and Ti4Fe7(V), it is confirmed that there is a mixed bonding of metallic, covalent and ionic nature in TiFe2 and Ti4Fe7(V) compounds, and the bonding of covalent feature weakens with the addition of V atom in TiFe2, which is the main reason for the improvement of the plasticity. Overall, these results would provide useful data for further investigating the magnetic properties of TiFe2 phase, and for future design of new structural alloys.
References
[1] ROSS J W, CRANGLE J. Magnetization of cubic Laves phase compounds of rare earths with cobalt [J]. Phys Rev, 1964, 133(2A): 509-510.
[2] MCDERMOTT M J, MARKLUND K K. Partial quenching of rare earth moment in cubic laves intermetallic compounds [J]. J Appl Phys, 1969, 40(3): 1007-1008.
[3] KOBLE J, HUTH M. Preparation and structural analysis of Fe2+xTi1-x thin films in the C14 Laves phase stability range [J]. J Cryst Growth, 2002, 234(4): 666-678.
[4] ORMECI A, CHU F, WILLS J M, MITCHELL T E, ALBERS R C, THOMA D J, CHEN S P. Total-energy study of electronic structure and mechanical behavior of C15 Laves phase compounds: NbCr2 and HfV2 [J]. Phys Rev B, 1996, 54(8): 12753-12762.
[5] LIU C T, ZHU J H, BRADY M P, MCKAMEY C G, PIKE L M. Physical metallurgy and mechanical properties of transition-metal Laves phase alloys [J]. Intermetallics, 2000, 8(9-11): 1119-1129.
[6] HOFFMANN E, ENTEL P, WASSERMANN E, SCHWARZ K, MOHN P. Electronic structure and magnetovolume instabilities of the hexagonal laves phase compound Fe2Ti [J]. J Phys IV, 1995, 5(C2): 117-122.
[7] RAVINDRAN P, FAST L, KORZHAVYI P A, JOHANSSON B. Density functional theory for calculation of elastic properties of orthorhombic crystals: application to TiSi2 [J]. J Appl Phys, 1998, 84(9): 4891-4904.
[8] HE Yu-ding, QU Xuan-hui, HUANG Bo-yun. Effect of alloying elements on mechanical properties of TiCr2 laves phase [J]. Chin J Nonferrous Met, 1998, 8(4): 569-572. (in Chinese)
[9] VANDERBILT D. Soft self-consistent pseudopotentials in a generalized eigenvalue formalism [J]. Phys Rev B, 1990, 41(11): 7892-7895.
[10] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Phys Rev Lett, 1996, 77(18): 3865-3868.
[11] KRESSE G, JOUBERT D. From ultrasoft pseudopotentials to the projector augmented-wave method [J]. Phys Rev B, 1999, 59(3): 1758-1775.
[12] WERTHEIM G K, WERNICK J H, SHERWOOD R C. Model for the composition-dependent ferromagnetic to antiferromagnetic transition in Fe2Ti [J]. Solid State Commun, 1969, 7(18): 1399-1402.
[13] BROWN P J, DEPORTES J, OULADDIAF B. Magnetic structure of the Laves phase compound TiFe2 [J]. J Phys: Condens Matter, 1992, 4(49): 10015-10024.
[14] PELLOTH J, BRAND R A, KEUNE W. Local magnetic properties of the Fe2Ti Laves phase [J]. J Magn Magn Mater, 1995, 140-144(1): 59-60.
[15] BROYDEN C G. The Convergence of a Class of Double-rank minimization algorithms: 2. The New Algorithm [J]. J Inst Math Appl, 1970, 6: 222-231.
[16] SAHU B R. Electronic structure and bonding of ultralight LiMg [J]. Mater Sci Eng B, 1997, 49(1): 74-78.
[17] MEDVEDEVA M I, GORNOSTYREV Y N, NOVIKOV D L, MRYASOV O N, FREEMAN A J. Ternary site preference energies, size misfits and solid solution hardening in NiAl and FeAl [J]. Acta Mater, 1998, 46(10): 3433-3442.
[18] WU Meng-meng, WEN Li, TANG Bi-yu, PENG Li-ming, DING Wen-jiang. First-principles study of elastic and electronic properties of MgZn2 and ScZn2 phases in Mg-Sc-Zn alloy [J]. J Alloys Compd, 2010, 506(1): 412-417.
[19] DENG X H, FAN B B, LU W. First-principles investigations on elastic properties of α- and β-Ta4AlC3 [J]. Solid State Commun, 2009, 149(11-12): 441-444.
[20] BORN M, HUANG K. Dynamical theory of crystal lattices [M]. Oxford: Oxford University Press, 1954: 10-12.
[21] YAO Hong-zhi, OUYANG Li-zhi, CHING Wan-Yim. Ab initio calculation of elastic constants of ceramic crystals [J]. J Am Ceram Soc, 2007, 90(10): 3194-3204.
[22] PUGH S F. Relations between the elastic moduli and the plastic properties of polycrystalline pure metals [J]. Philos Magn Ser, 1954, 7(45): 823-843.
[23] TVERGAARD V, HUTCHINSON J W. Microcracking in ceramics induced by thermal expansion or elastic anisotropy [J]. J Am Ceram Soc, 1988, 71(3): 157-166.
[24] HAO Xian-feng, XU Yuan-hui, WU Zhi-jian, ZHOU De-feng, LIU Xiao-juan, MENG Jian. Elastic anisotropy of OsB2 and RuB2 from first-principles study [J]. J Alloys Compd, 2008, 453(1): 413-417.
[25] RAVINDRAN P, FAST L, KORZHAVYI P A, JOHANSSON B, WILLS J, ERIKSSON O. Density functional theory for calculation of elastic properties of orthorhombic crystals: Application to TiSi2 [J]. J Appl Phys, 1998, 84(9): 4891-4904.
[26] NYE J F. Physical properties of crystals [M]. Oxford: Clarendon Press, 1964: 1-18.
[27] LIN W, XU Jian-hua, FREEMAN A J. Electronic structure, cohesive properties, and phase stability of Ni3V, Co3V, and Fe3V [J]. Phys Rev B, 1992, 45(19): 10863-10871.
[28] NONG Zhi-sheng, ZHU Jing-chuan, CAO Yong, YANG Xia-wei, LAI Zhong-hong, LIU Yong. A first-principles study on the structural, elastic and electronic properties of the C14 Laves phase compounds TiX2(X=Cr, Mn, Fe) [J]. Physica B, 2013, 419: 11-18.
[29] SHI Yi-ming, YE Shao-long. First principles study on electronic structure and optical properties of quaternary arsenide oxides YZnAsO and LaZnAsO [J]. Journal of Central South University, 2011, 18(4): 998-1003.
[30] GUAN Y Z, ZHANG H Y, LI W. First-principles study on alloying stability, electronic structure, and mechanical properties of Al-based intermetallics [J]. Physica B, 2011, 406(5): 1149-1153.
(Edited by FANG Jing-hua)
Cite this article as: NONG Zhi-sheng, CUI Pu-chang, ZHU Jing-chuan, ZHAO Rong-da. Alloying effects of V on stability, elastic and electronic properties of TiFe2 via first-principles calculations [J]. Journal of Central South University, 2017, 24(7): 1551-1559. DOI: 10.1007/s11771-017-3560-3.
Foundation item: Project(51401099) supported by the National Natural Science Foundation of China; project(201501079) supported by the Doctor Startup Foundation of Liaoning Province, China
Received date: 2016-03-14; Accepted date: 2016-05-09
Corresponding author: NONG Zhi-sheng, Lecturer, PhD; Tel: +86-24-89724198; E-mail: nzsfir@163.com

