基于Kriging插值无网格法的动力弹塑性分析
熊勇刚1, 2,田万鹏1,陈科良1,陈云飞2 ,杜民献1,吴吉平1
(1. 湖南工业大学 机械工程学院,湖南 株洲,412007;
2. 东南大学 机械工程学院,江苏 南京,210000)
摘要:为了克服移动最小二乘近似难以准确施加本质边界条件的缺点,将滑动Kriging插值引入无单元Galerkin法中,与非线性瞬变动态理论相结合,提出动力弹塑性分析的Kriging插值无网格法,推导Kriging插值无网格法在动力弹塑性问题中的理论公式,给出求解方案。研究结果表明:采用所提方法计算仅需要离散节点的信息,因而处理变得简单;采用预校正形式的Newmark法进行时间离散,计算效率提高;通过2个经典数值算例与有限元软件ABAQUS的计算结果对比,验证了所提理论和方法的正确性与可行性。
关键词:无网格法;滑动Kriging插值;动力响应;弹塑性
中图分类号:O344 文献标志码:A 文章编号:1672-7207(2014)02-0435-06
Dynamic elastoplastic analysis by using meshless Kriging interpolation method
XIONG Yonggang1, 2, TIAN Wanpeng1, CHEN Keliang1, CHEN Yunfei2, DU Minxian1, WU Jiping1
(1. College of Mechanical Engineering, Hunan University of Technology, Zhuzhou 412007, China;
2. College of Mechanical Engineering, Southeast University, Nanjing 210000, China)
Abstract: Because the shape functions constructed by the moving least squares approximation do not possess the Kronecker delta property, accurate imposition of essential boundary conditions in the traditional element free Galerkin (EFG) method is often difficult, the moving Kriging interpolation procedure was introduced into EFG method to be the meshless Kriging interpolation method (MKIM). On the basis of MKIM and nonlinear transient dynamic theory, the MKIM for dynamic elastoplastic analysis was presented. The results show that only a group of discretized nodes is needed and therefore the preprocessing of this method is very simple. The predictor-corrector form of the Newmark algorithm is employed for the time integration scheme. Several numerical examples are presented to verify the validity and accuracy of the presented method.
Key words: meshless methods; moving Kriging interpolation; dynamic response; elastoplasticity
无网格方法近年来得到了较大发展,是目前科学和工程计算方法研究的热点之一[1-3]。与有限元法不同,无网格方法的近似函数是建立在一系列离散点上的,可以部分或彻底消除网格,从而有效地避免了由于网格的依赖性而带来的种种困难。目前,发展的无网格方法主要有无单元Galerkin法[4-5]、无网格局部Petrov-Galerkin法[6]、光滑粒子流体动力学法[7-8]、再生核粒子法[9]、复变量无网格方法[10]、边界无单元法[11-12]、无网格流形方法[13]以及自然单元法[14]等,其中,无单元Galerkin法是发展良好和最具有应用价值的无网格方法之一[1],但该法的最大缺点是采用移动最小二乘法构造的形函数不满足Kronecker delta函数性质,因此,本质边界条件的施加非常困难,需要采用特别技术进行处理。Kriging插值无网格法是在构造形函数时采用滑动Kriging插值代替移动最小二乘法而发展起来的一种改进的无单元Galerkin法。滑动Kriging插值法构造近似函数不仅数值实现简单、计算量小,而且满足Kronecker delta函数性质,从而可以非常方便地施加本质边界条件[15-16]。为此,本文作者将Kriging插值无网格法应用于动力弹塑性问题的求解计算。首先详细推导Kriging插值无网格法在动力弹塑性问题中的理论公式,然后,给出基于Kriging插值无网格法的动力弹塑性分析的数值实现方法和具体算例。
1 滑动Kriging插值
与移动最小二乘法相似,假设任意计算点x的影响域内包含n个节点。滑动Kriging插值的逼近函数采用如下线性回归模型与偏差之和的模式:
 (1)
(1)
式中:pT(x)为多项式基函数;a为待求常系数向量;z(x)为一个均值为0、方差为σ2、协方差不为0时的局部离差。对于二维情况,p(x)可选取如下二次基:
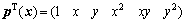 (2)
(2)
用式(1)对n个样本点进行插值,则z(x)的协方差可表示为
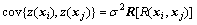 (3)
(3)
式中: 是对角线为单位1的对称相关矩阵;
是对角线为单位1的对称相关矩阵;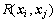 为任意2点xi和xj之间的相关函数,通常可以取为
为任意2点xi和xj之间的相关函数,通常可以取为
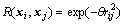 (4)
(4)
θ>0,为模型参数;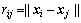 为给定2点xi和xj之间的相关距离。
为给定2点xi和xj之间的相关距离。
计算点x与所给定的n个节点之间的相关函数向量为
 (5)
(5)
在给定的n个节点处的函数值已知时,
 (6)
(6)
式中:u为n个节点处场函数的集合。当采用线性回归模型式(1)表达u时,有
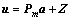 (7)
(7)
式中:Pm与Z分别为给定点上基函数值所形成的矩阵及线性逼近的误差向量,且有
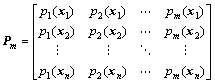 (8)
(8)
 (9)
(9)
对计算点x,采用已知节点的函数值对场函数u(x)进行线性逼近,有
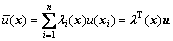 (10)
(10)
于是,式(1)与式(10)之间的误差函数为

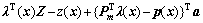 (11)
(11)
要保证无偏估计,必须满足如下约束条件:
 (12)
(12)
式(11)中误差函数的均方差为
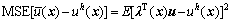 (13)
(13)
为了确定最优的线性估计,将式(13)作为目标函数,式(12)作为约束条件,进而根据Lagrange不定乘子法可以将其转化为无条件的极小值问题。通过对向量λT(x)求偏导数为0得到一组方程,求解此方程组可得到最优线性无偏估计条件下的插值函数[15-16]:
 (14)
(14)
式中:
 (15)
(15)
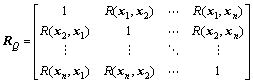 (16)
(16)
同时,为了便于表述,定义
 (17)
(17)
式中:I为n×n阶单位矩阵。于是,式(14)可改写为
 (18)
(18)
式中: 和
和 分别为形函数矩阵和形函数,
分别为形函数矩阵和形函数,
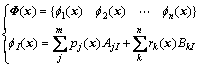 (19)
(19)
AjI为矩阵A的第j行、第I列元素;BkI为矩阵B的第k行、第I列元素。
形函数 关于x和y的导函数分别为
关于x和y的导函数分别为
 (20)
(20)
2 动力弹塑性分析的Kriging插值法
2.1 控制方程
考虑二维动力弹塑性问题,其计算域为Ω,边界为 ,控制方程为:
,控制方程为:
 (21)
(21)
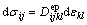 (22)
(22)
 (23)
(23)
式中:ρ为质量密度; 为节点加速度,且有
为节点加速度,且有 ;ui为节点位移;t为时间;σij为应力;εij为应变;bi为体力;
;ui为节点位移;t为时间;σij为应力;εij为应变;bi为体力;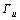 和
和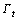 分别为位移和面力已知的边界。采用von Mises屈服准则、关联流动准则和各向同性硬化准则时,式(22)中的弹塑性
分别为位移和面力已知的边界。采用von Mises屈服准则、关联流动准则和各向同性硬化准则时,式(22)中的弹塑性 可以写为
可以写为
 (24)
(24)
其中:
 (25)
(25)
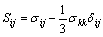 (26)
(26)
σeq和H分别为等效应力和塑性模量;G和v分别为剪切模量和泊松比。
应力和位移满足如下边界条件
 (27)
(27)
和初始条件
 (28)
(28)
式中:nj(x)为 上点x处的外法线方向余弦;
上点x处的外法线方向余弦; 和
和 分别为已知的位移和面力分量;u0和v0分别为初始位移和初始速度。
分别为已知的位移和面力分量;u0和v0分别为初始位移和初始速度。
2.2 空间离散
平衡方程式(21)的弱形式可以通过加权残值法获得,即
 (29)
(29)
式中:wi为权函数。对式(29)进行分部积分,并考虑到自然边界条件式(27),有
 (30)
(30)
由于只对空间域进行离散,求解域Ω内的试函数 可以由式(18)表示为
可以由式(18)表示为
 (31)
(31)
将空间离散后的位移表达式(31)代入式(30),且令权函数等于形函数,最终可得弹性动力学的离散方程为
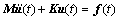 (32)
(32)
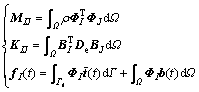 (33)
(33)
式中:M,K和f(t)分别为质量矩阵、刚度矩阵与载荷向量;
 ,
, (34)
(34)
对于动力弹塑性问题,式(32)可以改写为
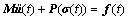 (35)
(35)
节点内力向量 为
为
 (36)
(36)
其中: 为应力向量。
为应力向量。
2.3 求解方案
本文采用传统的Newmark方法对时间域进行离散。Newmark法于1959年由线性加速度法延伸推导而得,是一种应用相当广泛的直接积分法。由于塑性变形的非线性特性,在每个时间步都必须进行迭代计算。在t和t+△t时间步内的迭代求解过程如下[17-19]:
(1) 令迭代计算变量k=0;
(2) 在开始预估阶段,令
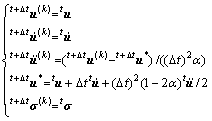 (37)
(37)
(3) 利用下述方程计算残余力:
 (38)
(38)
(4) 如有需要,应用下式形成等效刚度矩阵:
 (39)
(39)
否则,就应用前面已计算的K*。
(5) 求解方程:
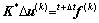 (40)
(40)
得到节点位移增量 ,然后,计算每个高斯点的应力
,然后,计算每个高斯点的应力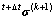 。
。
(6) 进入修正阶段,令
 (41)
(41)
式中:α和△是按积分精度和稳定性要求决定的参数。当△≥0.5和α≥0.25(0.5+△)2时算法是无条件稳定的,即时间步长△t不影响解的稳定性。
(7) 迭代收敛检查。对于给定的收敛误差εR,若||△u(k)||≤εR,则结束本时间步内的迭代循环,否则,令k=k+1并转到第3步。
(8) 为了使下一个时间步使用,令
 (42)
(42)
给定初始位移u0和初始速度v0后,可以从下式求出初始加速度 :
:
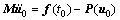 (43)
(43)
3 数值算例
为了验证以上提出的数值方法的有效性,本文分析2个算例。在滑动Kriging插值中,本文选用二次基函数,并且计算点x的影响域取为以点x为圆心的圆形域,半径dmax=scale×s[6](其中s[6]为计算点x到距其最近的第6个节点之间的距离),系数scale取为2.5。
算例1 受内压作用的厚壁圆筒。
1个内径a=1 m,外径b=2 m的厚壁圆筒,受到p=1.85×104 Pa的突加内压作用,如图1所示。材料为理想弹塑性,并服从von Mises屈服准则。材料的弹性模量E=2.1×107 Pa,泊松比ν=0.3,屈服应力σy=3.55×104 Pa,质量密度ρ=7.85 kg/m3。该问题为平面应变状态下的1个经典算例。

图1 受内压作用的厚壁圆筒
Fig. 1 A thick-walled cylinder subjected to internal pressure
由于对称性,可取结构的1/4作为计算模型。计算分析中采用图1(a)所示的节点布置方案,且时间步长取为△t=1.0×10-5 s。图2所示为内表面的径向位移随时间的变化曲线。为了进行对比,图2还给出了有限元软件ABAQUS的计算结果。从图2可以看出:本文的计算结果与ABAQUS的计算结果很吻合,说明本文推导的动力弹塑性分析的Kriging插值无网格法及其离散形式是正确的,方法是可行的。

图2 内表面的径向位移
Fig. 2 Radial displacement history at inner surface
算例2 受突加载荷的悬臂梁。
如图3所示为长L=1.2 m、高H=0.4 m的悬臂梁,在平面应力状态下端部受到突加剪切荷载p=2.5 kPa的作用。材料为理想弹塑性,并服从von Mises屈服准则。材料弹性模量E=2.1×107 Pa,泊松比ν=0.3,屈服应力σy=4.0×104 Pa,质量密度ρ=7.85 kg/m3。
在计算时,把区域均匀地划分为25×7个节点的网格,且时间步长取为△t=1.0×10-4 s。为了检验方法的有效性,本文使用有限元软件ABAQUS的计算结果进行对比。图4所示为悬臂梁右端中点A的竖向位移随时间的变化曲线。从图4可以看出:本文的计算结果与ABAQUS的计算结果很吻合,从而进一步验证了本文方法的有效性。
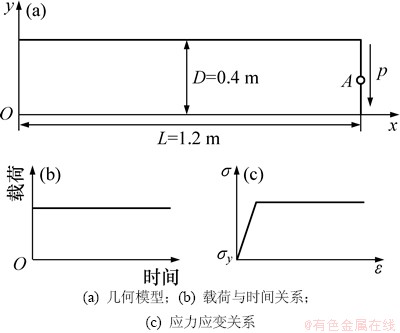
图3 受突加载荷的悬臂梁
Fig. 3 Cantilever beam under Heaviside loading

图4 悬臂梁中A点的竖向位移
Fig. 4 Vertical displacement of point A in beam
4 结论
(1) 采用Kriging插值无网格法,建立了进行结构弹塑性动力响应分析的一种新方法,推导了相应的计算公式,提出了具体的数值实现方法。数值计算结果表明,采用Kriging插值无网格法进行动力弹塑性分析是可行的,它具有稳定性好和精度高等优点。
(2) 采用Kriging插值无网格法进行动力弹塑性分析只需要离散节点的信息,从而减少了前处理的工作量。尤为重要的是,滑动Kriging插值法的形函数满足Kronecker delta函数性质,因而能够直接、准确地施加本质边界条件。此外,形函数导数的计算不涉及逆矩阵的求导,因而计算效率较高。
参考文献:
[1] Belytschko T, Krongauz Y, Organ D, et al. Meshless methods: An overview and recent developments[J]. Computer Methods in Applied Mechanics and Engineering, 1996, 139: 3-47.
[2] Li S F, Liu W K. Meshfree and particle methods and their applications[J]. Applied Mechanics Review, 2002, 55: 1-34.
[3] 宋康祖, 陆明万, 张雄. 固体力学中的无网格方法[J]. 力学进展, 2000, 30(3): 55-65.
SONG Kangzu, LU Mingwan, ZHANG Xiong. Meshless method for solid mechanics[J]. Advance in Mechanics, 2000, 30(3): 55-65.
[4] Belytschko T, Lu Y Y, Gu L. Element-free Galerkin method[J]. International Journal for Numerical Methods in Engineering, 1994, 37: 229-256.
[5] 王东东, 李凌, 张灿辉. 稳定节点积分伽辽金无网格法的应力计算方法研究[J]. 固体力学学报, 2009, 30(6): 586-591.
WANG Dongdong, LI Ling, ZHANG Canhui. On stress evaluation in Galerkin meshfree methods with stabilized conforming nodal integration[J]. Chinese Journal of Solid Mechanics, 2009, 30(6): 586-591.
[6] Atluri S N, Zhu T L. A new meshless local Petrov-Galerkin(MLPG) approach in computational mechanics[J]. Computational Mechanics, 1998, 22(2): 117-127.
[7] Gingold R A, Monaghan J J. Smoothed particle hydrodynamics: theory and application to non-spherical stars[J]. Monthly Notices of the Royal Astronomical Society, 1977, 181: 375-389.
[8] 缪吉伦, 陈景秋, 张永祥. 基于SPH方法的立面二维涌浪数值模拟[J]. 中南大学学报(自然科学版), 2012, 43(8): 3244-3249.
MIAO Jilun, CHEN Jingqiu, ZHANG Yongxiang. Two-dimension numerical simulation of impulsive waves by SPH method[J]. Journal of Central South University (Science and Technology), 2012, 43(8): 3244-3249.
[9] Liu W K, Jun S, Zhang Y F. Reproducing kernel particle methods[J]. International Journal for Numerical Methods in Fluids, 1995, 20: 1081-1106.
[10] 程玉民, 李九红. 弹性力学的复变量无网格方法[J]. 物理学报, 2005, 54(10): 4463-4471.
CHENG Yumin, LI Jiuhong. A meshless method with complex variables for elasticity[J]. Acta Physica Sinica, 2005, 54(10): 4463-4471.
[11] 程玉民, 陈美娟. 弹性力学的一种边界无单元法[J]. 力学学报, 2003, 35(2): 181-186.
CHENG Yumin, CHEN Meijuan. A boundary element-free method for linear elasticity[J]. Chinese Journal of Theoretical and Applied Mechanics, 2003, 35(2): 181-186.
[12] 程玉民, 彭妙娟. 弹性动力学的边界无单元法[J]. 中国科学, 2005, 35(4): 435-448.
CHENG Yumin, PENG Miaojuan. Boundary element-free method for elastodynamics[J]. Science in China, 2005, 35(4): 435-448.
[13] 李树忱, 李术才, 朱维申. 弹性动力学的无网格流形方法[J]. 岩石力学与工程学报, 2006, 25(1): 141-145.
LI Shuchen, LI Shucai, ZHU Weishen. Study on meshless manifold method in elastodynamics[J]. Chinese Journal of Rock Mechanics and Engineering, 2006, 25(1): 141-145.
[14] Sukumar N, Moran B, Belytschko T. The natural elements method in solid mechanics[J]. International Journal for Numerical Methods in Engineering, 1998, 43: 839-887.
[15] Gu L. Moving kriging interpolation and element-free Galerkin method[J]. International Journal for Numerical Methods in Engineering, 2003, 56: 1-11.
[16] Dai K Y, Liu G R, Lim K M, et al. Comparison between the radial point interpolation and the kriging interpolation used in meshfree methods[J]. Computational Mechanics, 2003, 32: 60-70.
[17] Soares D Jr, Sladek J, Sladek V. Nonlinear dynamic analyses by meshless local Petrov-Galerkin formulations[J]. International Journal for Numerical Methods in Engineering, 2010, 81: 1687-1699.
[18] 陈莘莘, 李庆华, 刘应华, 等. 动力弹塑性分析的无网格自然单元法[J]. 固体力学学报, 2011, 32(5): 493-499.
CHEN Shenshen, LI Qinghua, LIU Yinghua, et al. Application of meshless natural element method to dynamic elastoplastic analysis[J]. Chinese Journal of Solid Mechanics, 2011, 32(5): 493-499.
[19] Owen D J R, Hinton E. Finite element in plasticity: Theory and practice[M]. Swansea: Pineridge Press, 1980: 431-463.
(编辑 陈灿华)
收稿日期:2013-06-10;修回日期:2013-08-22
基金项目:国家自然科学基金资助项目(51345005);江苏省博士后基金资助项目(1202003B);湖南省自然科学基金资助项目(13JJ9014)
通信作者:吴吉平(1966-),男,湖南益阳人,副教授,从事机械设计及理论研究;电话:0731-22183429;E-mail:wjp0918@163.com