J. Cent. South Univ. (2018) 25: 418-431

DOI: https://doi.org/10.1007/s11771-018-3747-2

Bayesian framework for satellite rechargeable lithium battery synthesizing bivariate degradation and lifetime data

ZHANG Yang(张洋), JIA Xiang(贾祥), GUO Bo(郭波)

College of Information Systems and Management, National University of Defense Technology,Changsha 410073, China

Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018

Abstract: Reliability and remaining useful life (RUL) estimation for a satellite rechargeable lithium battery (RLB) are significant for prognostic and health management (PHM). A novel Bayesian framework is proposed to do reliability analysis by synthesizing multisource data, including bivariate degradation data and lifetime data. Bivariate degradation means that there are two degraded performance characteristics leading to the failure of the system. First, linear Wiener process and Frank Copula function are used to model the dependent degradation processes of the RLB’s temperature and discharge voltage. Next, the Bayesian method, in combination with Markov Chain Monte Carlo (MCMC) simulations, is provided to integrate limited bivariate degradation data with other congeneric RLBs’ lifetime data. Then reliability evaluation and RUL prediction are carried out for PHM. A simulation study demonstrates that due to the data fusion, parameter estimations and predicted RUL obtained from our model are more precise than models only using degradation data or ignoring the dependency of different degradation processes. Finally, a practical case study of a satellite RLB verifies the usability of the model.

Key words: rechargeable lithium battery; Bayesian framework; bivariate degradation; lifetime data; remaining useful life; reliability evaluation

Cite this article as: ZHANG Yang, JIA Xiang, GUO Bo. Bayesian framework for satellite rechargeable lithium battery synthesizing bivariate degradation and lifetime data [J]. Journal of Central South University, 2018, 25(2): 418–431. DOI: https://doi.org/10.1007/s11771-018-3747-2.

1 Introduction

A rechargeable lithium battery (RLB) has various desirable characteristics of high energy density, long mission life, high operating discharge voltage levels, no memory effect, and others [1, 2], which make it to be a critical component of the electrical power system for long life spacecraft [3]. In recent decades, the power requirement is growing from several watts to several kilowatts with a life of 15–20 years [4]. Failure of a RLB may result in operational disability, sometimes even the catastrophic failure of the entire spacecraft [5]. For the reason of high reliability requirement, a RLB used for satellite power system should have as long and high as possible mission life. Hence it is increasingly essential to assess its real-time reliability and predict the remaining useful lifetime (RUL) of the RLB for prognostic and health management.Unfortunately, limited reliability information causes great difficulties in reliability assessment and RUL estimation for these high- performance satellite components while orbiting in outer space. This paper aims to synthesize all measurable but limited multi-source data, including on-orbit bivariate degradation data of the RLB of interest and the lifetime data of congeneric RLBs, to carry out relevant reliability analysis.

In recent years, it has witnessed an increasing research interest in RUL prediction of lithium battery based on various performance characteristics (PCs). Currently, there are two main types of models for RUL prediction, i.e., physics- of-failure (PoF) and data-driven model [6]. While numerous PoF models have been illustrated the internal dynamics of lithium batteries [7–9], but these models are not applicable to real-time RUL prediction of the on-line RLB due to the complex and changing natural space environments. Aiming at this problem, data-driven approaches based on degradation data of diverse PCs of a RLB are recommended. Owing to irreversible physical and chemical processes, the performance of a RLB drops inevitably over service time. Among numerous PCs, capacity is the most common indicator to directly diagnose the battery’s degradation degree [10–12]. Unfortunately, it has difficulties in collecting on-orbit capacity fading data of a satellite RLB. This is because battery might not be discharged from 100% SOC to 0% SOC or charged from 0% SOC to 100% SOC, and such internal state variables are inaccessible via general sensors [13]. However, researches showed that capacity decrease, and power fading of the battery did not originate from a single cause, but from various processes and their interactions [14]. Therefore, other measurable PCs as alternatives are taken into consideration as the health indicator to give a statement about a RLB’s on-line operating condition, such as charge and discharge voltage, temperature and current [13]. Most existing work about RUL prediction only deals with one- dimensional degradation data. In practice, WANG et al [15] pointed out that many products had two or more PCs charactering their performance. In this paper, study is based on a practical project, in which only degradation data of temperature and discharge voltage are collected. The two health indicators, as the most available monitoring data, are simultaneously considered in our degradation model for on-line degradation analysis. More information of the project is given in Section 4.2.

Existing references pointed out the feasibility of the two PCs to be the health indicators. CHEN et al [16] demonstrated that the thermal behavior of lithium batteries is significant for service life requirements and safety considerations. GAO et al [1] also mentioned the temperature could indicate the heat sinking of a battery which affected its operation. Hence, on-orbit temperature degradation data can be used to implement the RUL prediction. In addition, discharge voltage is another common measurable PC that can imply the decrease of battery’s performance [13, 17]. CHOI and WANG [18] argued that the temperature and discharge voltage were closely related, and they built a voltage–temperature limit circuit for satellite power system to analyze their performance. Therefore, it is reasonable and necessary to take account of these two PCs together.

According to the two PCs’ degradation paths, the degradation processes are governed by a linear Wiener process. Given a predetermined degradation threshold, the first hitting time when the degradation exceeds a given threshold follows an inverse Gaussian distribution [19]. PAN et al [20] proposed to use Copula function to describe the dependency of two PCs, constructing a joint distribution of the RUL. To simplify the model, PAN et al [20] and WANG et al [15, 21] all assumed that the single degradation process was non-decreasing, then the same Copula function could be used in both statistical models of the degradation increments and the RUL distribution. However, this assumption of monotony is unsuitable for modeling the PCs of a satellite RLB. Furthermore, it is not reliable enough to obtain the real-time RUL prediction and reliability evaluation only based on small on-orbit degradation data, because the ageing of several selected PCs may not depict the entire healthy conditions of a RLB. And, in consideration of the complex natural space environments, we do not advise to utilize the population degradation data from laboratory. This is because it is hard to simulate the actual space conditions in laboratory or to use other methods to eliminate the differences between the laboratory test condition and the field condition. Fortunately, from congeneric satellite RLBs running in the same environment, we can collect several lifetime data of extremely small size, even some of which are just zero-failure data. This kind of lifetime data might be useless to predict the RUL alone. But it can be an effective supplement of the limited on-orbit degradation data and it provides possibilities to tackle aforementioned problems.

To take full advantages of the multi-source information, Bayesian method has been widely applied to data fusion in satellite reliability engineering [22, 23]. Recently, a lot of work has been done to integrate univariate degradation testing data and field lifetime information for reliability assessing, which turned out to be effective to increase the accuracy of parameter estimation [24–26]. However, at present, there is no attempt on information fusion of bivariate degradation and lifetime data. Aiming at this, Copula functions are firstly used to characterize the dependency of the two PCs. Next, a novel Bayesian framework is put forward to synthesize bivariate degradation data and lifetime data for RUL prediction and reliability evaluation of a satellite RLB. Regarding the complexity of the model and the high dimension of the unknown parameter vector, Markov Chain Monte Carlo (MCMC) algorithm is introduced to estimate parameters. Besides, an introduction of a model selection criterion named deviance information criterion (DIC) is given for model comparison. Compared to another four models only based on degradation data or ignoring the dependency of two PCs, our novel approach performs better due to DIC.

Figure 1 shows the novel Bayesian framework proposed. Then the paper is organized as follows. Section 2 introduces the bivariate degradation model based on Copula function, as well as models for reliability evaluation and RUL prediction considering two PCs of the satellite RLB. Section 3 introduces the Bayesian framework to synthesize bivariate degradation and lifetime data. In addition, a brief introduction of MCMC algorithm is given in this section. Section 4 presents a simulation study to make a comparison between the novel Bayesian framework and another four models. In addition, a practical case study is provided to verify the usability of the model.Finally, conclusions are drawn in Section 5.

2 Models

In this section, Frank Copula function is introduced. Then, the bivariate Wiener degradation model can be built via Frank Copula function. Further, the joint reliability function and the RUL distribution are obtained for further analysis.

2.1 Frank Copula function

Copulas are functions that join or “couple” multivariate distribution functions to their one- dimensional marginal distribution functions [27], which is a way to study scale-free measures of dependency. Much work has been done to apply Copulas to bivariate or multiple degradation modeling [20, 28]. The central theory of Copulas is Sklar’s Theorem [29], providing the theoretical foundation for applications of Copulas.

Sklar’s Theorem. Let H be a joint distribution function with margins F₁ and F₂. Then there exists a Copula C(·) such that for all x and y in R,

                    (1)

If F₁ and F₂ are continuous, then C(·) is unique; otherwise, C(·) is uniquely determined on RanF₁× RanF₂, where RanF_k (k=1, 2) is the range of F_k. Conversely, if C(·) is a Copula and F₁ and F₂ are distribution functions, then the function H(·) defined by Eq. (1) is a joint distribution function with the margins F₁ and F₂.

Figure 1 Novel Bayesian framework for reliability evaluation and RUL prediction

There are several flexible and convenient families of Copulas to combine the marginal distributions. Archimedean Copulas are a popular class of Copulas because they allow modeling dependency in arbitrarily high dimensions with only one parameter. PAN et al [20] made a comparison between four Copula functions to model the bivariate degradation process and concluded that the Frank Copula function performed better than others. We might as well use Frank Copula function expressed as

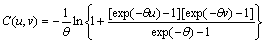   (2)

and the corresponding PDF is

(3)

where Let C_u(v) be the partial derivative with respect to variable u, expressed as

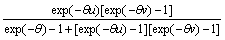    (4)

2.2 Bivariate degradation model

Degradation data can measure some qualities about a product or a component that is indirectly related to reliability or lifetime. In this subsection, a bivariate degradation model is proposed for two PCs of a satellite RLB. Considering the case that for the kth PC (k=1, 2), there are n on-orbit measurements of the degradation process, denoted as {X_k(t_i)}, where t_i is the measurement time and i=1, 2, …, n.

2.2.1 Wiener process and univariate degradation model

It is assumed that each PC’s degradation process follows a linear Wiener process with drift parameter μ_k and diffusion parameter σ_k (k=1, 2). The degradation model at time t_i (i=1, 2, …, n) is defined by

              (5)

where B(t) is the standard Brownian motion process representing a time correlated structure with the mean value of 0 and the variance of t_i, denoted as B(t_i)~N(0, t_i). For simplicity, let X_k(t₀) be 0, and X_k(t_i) represent the cumulative degradation increment. For an individual component, we assume that the drift parameter μ_k and diffusion parameter σ_k can be regarded as constants during a certain measurement period, but their estimates obtained at different measurement time may be distinct due to the different sample size of degradation data.

Owing to the good mathematical properties of Wiener process, it is widely used to model the battery degradation process [3, 30]. Wiener process is a continuous-time stochastic process with stationary and independent increments, which means that the degradation increment ΔX_k(t_i) during the time t_i–1 to t_i is normally distributed, that is

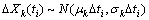                   (6)

where and Δt_i=t_i–t_i–1. So, the probability density function (PDF) of ΔX_k(t_i) is

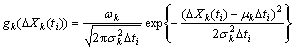(7)

and the cumulative distribution function (CDF) of ΔX_k(t_i) is

            (8)

where Φ(·) denotes the CDF of the standard normal distribution and i=1, 2, …, n, k=1, 2.

2.2.2 Bivariate degradation model

For a satellite RLB, degradation mechanisms are often inter-dependent. Sometimes, two or more PCs can indicate the ageing phenomena during the working period. Taking consideration of all the PCs and the dependency between them to model the degradation process is essential to predict the RUL and evaluate the reliability.

Let X(t_i)=(X₁(t_i), X₂(t_i)) be the degradation measurements of two PCs of a satellite RLB at time t_i, for i=1, 2, …, n. Correspondingly, degradation increment is denoted as ΔX(t_i)=(ΔX₁(t_i), ΔX₂(t_i)). For simplicity, it might as well ignore the dependency between ΔX₁(t_i) and ΔX₂(t_j), when i≠j, and just consider the relationship between ΔX₁(t_i) and ΔX₂(t_i). Due to the Sklar’s theorem and Copulas theory, the joint distribution function of ΔX₁(t_i) and ΔX₂(t_i) is written as

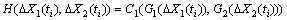(9)

where C₁(·) is a specific Copula function with parameter θ₁. The joint PDF of 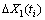and is written as

(10)

where c₁(·) is the PDF of Frank Copula in form of Eq.(3).

2.3 Model for reliability evaluation

Assume that the failure of a satellite RLB is caused by performance degradation. Suppose that the initial degradation increment equals zero and μ_k>0, let ω_k be the failure threshold of the kth PC. When only one PC is considered, it is known that the lifetime T_k of a Wiener process follows an inverse Gaussian distribution [19, 31], written as

          (11)

and the CDF is

             (12)

When there are two PCs leading to the failure of the system, let define T to be the lifetime of a satellite RLB in consideration of bivariate PCs. It can be written as

                          (13)

Then the reliability function is

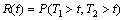                     (14)

According to Sklar’s theorem, given ω₁ and ω₂, there exists another Frank Copula function satisfying

                     (15)

where R_k(t)=P(T_k>t)=1–F_k(t). Then the PDF f(t) is

              (16)

Note that the Frank Copula function C₂(·) should be different from C₁(·) in Eq. (9). In Refs. [15, 20], to simplify the model, authors assumed that the marginal degradation data of the two PCs are non-decreasing functions of time. Then C₂(·) can be approximated by C₁(·). However, this assumption is too strong, restricting the application of the model. Fortunately, by synthesizing the lifetime data, the different unknown parameter θ₂ can be estimated and the monotony assumption can be ignored.

2.4 Model for RUL estimation

When only one PC is considered, given that the kth PC does not exceed the failure threshold ω_k>0 at the given time t_h (h=1, 2, …, n), the RUL denoted as L_kh only considering the kth PC is

 (17)

According to Eq. (5), X_k(t_h+l) can be expressed as

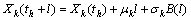            (18)

Let Y_k(l)=X_k(t_h+l)–X_k(t_h), then Y_k(0)=0, and Y_k(k) is a linear Wiener process. Now the transformed failure threshold at time t_h is ω_k(t_h)=ω_k–X_k(t_h). Then the PDF of L_kh is

      (19)

and the corresponding CDF of L_kh is

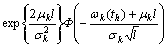            (20)

When there are two PCs, according to Eq. (16), the joint PDF of the RUL of the bivariate degradation process is

           (21)

where R_kh(l)=1–F_kh(l)..

3 Bayesian framework for reliability evaluation and RUL estimation

3.1 Bayesian method

In this work, a Bayesian framework is proposed to construct the prior joint distribution of all unknown parameters by synthesizing degradation data and lifetime data. After that, Bayesian theorem is applied to posterior distribution construction to obtain the estimations.

In Bayesian theorem, the unknown parameters are treated as random variables, following some distributions. If we have observed the on-orbit degradation increments of temperature and discharge voltage of a satellite RLB, represented by ΔX₁=(ΔX₁(t₁), ΔX₁(t₂), …, ΔX₁(t_n)) and ΔX₂= (ΔX₂(t₁), ΔX₂(t₂), …, ΔX₂(t_n)) respectively, and a group of lifetime data D={ξ₁, ξ₂, …, ξ_p, η₁, η₂, …, η_q}, due to Eqs. (10) and (16), the total likelihood function is

  (22)

where Θ=(μ₁, σ₁, μ₂, σ₂, θ₁, θ₂) is the unknown parameter vector.

To facilitate the parameter estimation by MCMC method using the software WinBUGS in the following step, a Bernoulli-ones strategy is used to indirectly specify any arbitrary model likelihood [32]. Let us transform the likelihood function in Eq. (22) to the log-likelihood form as

                     (23)

where

         (24)

Then the likelihood model can be rewritten in a simple form as

            (25)

whereis the binomial probability function with success probability 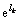and total test number N=1. Hence, the likelihood function can be written as the product of the densities of new pseudo random variables with all observed values set to be one, and these new random variables now follow the Bernoulli distribution with the success probability equal to .

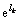According to the Bayesian theorem, the posterior distribution is

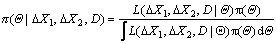
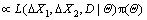               (26)

where π(Θ) is the joint prior distribution of μ₁, σ₁, μ₂, σ₂, θ₁ and θ₂.

In Bayesian method, prior distributions are used to describe the uncertainty of the unknown model parameters. The selection of the prior distributions is the subjective part in Bayesian method, which is important for the parameter estimation. In Ref. [33], PENG gave a specific discussion on the optimal prior PDF selection for the degradation tests. For simplicity, JIN et al [3], WANG et al [34] and YUAN et al [35] assumed that all parameters of inverse Gaussian distribution have independent prior distributions. And μ_k (k=1, 2) follows the normal distribution and σ_k (k=1, 2) follows the inverse gamma distribution. The priors of θ₁ and θ₂ are both normal distributions as PAN [20] recommended. Thus, the total joint prior is

            (27)

3.2 Parameter estimation

In this subsection, we introduce the MCMC method to estimate unknown parameters in Bayesian inference. MCMC algorithm provides an alternative way to simulate large enough samples from the complicated posterior distribution based on a Markov Chain in order to estimate the corresponding posterior distributions with accuracy. In this way, MCMC method has greatly contributed to the development and propagation of Bayesian theory. The two most popular MCMC methods are the Metropolis-Hasting (M-H) algorithm and the Gibbs sampling. Here a brief introduction of M-H algorithm is provided.

In Bayesian framework, let us assume that the posterior distribution is f(θ|y) from which we wish to generate a sample of size T. Denote θ^(t) to be the vector of generated values in the t generation of the algorithm and y are the data. The procedure of M-H algorithm is summarized as follows [32]:

1. Set initial values θ⁽⁰⁾

2. For t=1, 2, …, T, repeat the following steps

a. Set θ=θ^(t–1).

b. Generate new candidate parameter value θ′ from a proposal distribution q(θ→θ′)= q(x′|x).

c. Compute

.

d. Update θ^(t)=θ′ with probability α; otherwise, set θ^(t)=θ.

The other popular MCMC method, the Gibbs sampler, is just a special case of M-H algorithm with fixed probability α=1. To implement the algorithm, WinBUGS software is a convenient tool by using MCMC techniques to evaluate Bayesian models. And the Bernoulli-ones strategy is applied to demonstrate the statistic model. More information about MCMC method and WinBUGS can refer to Ref. [32].

4 Numerical example

4.1 Simulation study

In this subsection, a simulated numerical example about a satellite RLB is presented to illustrate the validity of the proposed approach. First, simulated dependent bivariate degradation data of two PCs are generated using the simulation method proposed by PAN et al [36]. Then, the parameter estimation results using MCMC algorithm are obtained. And DIC is applied to model comparison. Based on the estimation results, RUL prediction and reliability evaluation are carried out. Finally, relative error of predicted RUL is defined to quantitatively check the validity and analyze the precision of the proposed model.

4.1.1 Data simulation

The simulated data are generated via the method proposed by PAN et al [36]. The detailed steps to implement the data simulation are presented in appendix. We assume that there are three RLBs with two PCs (temperature and discharge voltage) coming from the same population. Both bivariate degradation processes have a decreasing tendency governed by Wiener processes. The parameter vector of the proposed model is denoted as θ=(θ₁, θ₂, μ₁, μ₂, σ₁, σ₂). The model parameter settings used for the simulation are θ=(0.95, 0.2, 0.50, 0.60, 0.40, 0.55). The initial values of the two PCs are X₁=5.5 °C and X₂=50.3 V, which are set according to a real project that we will mention later. The degradation time unit is in year and the failure thresholds of two PCs are respectively ω₁=1.5 °C, ω₂=45 V. The simulated lifetime of the three RLBs are respectively ξ₁=6.51 year, ξ₂=6.30 year and ξ₃=6.44 year. We treat the first and the second RLB as congeneric products of the third one of interest. Thus, RUL prediction and reliability evaluation of the third RLB will be conducted by synthesizing the lifetime data of the previous two RLBs and the degradation data of itself. Figure 2 shows the 100 groups of temperature and discharge voltage degradation data within the third RLB’s overall lifetime (around 6.44 years).

4.1.2 Parameter estimation

In this simulated numerical example, another four existing models are compared with the Bayesian framework model that we propose. Let M₁, M₂, M₃, M₄ and M₅ denote the five models, and the definition is:

1) M₁: The Bayesian framework proposed in this work. The two PCs are dependent, characterized by Frank Copula function, and failure lifetime data are synthesized in the model.

2) M₂: Consider the two PCs to be independent and failure lifetime data are incorporated in the model

3) M₃: Only use the bivariate degradation data without considering dependency

4) M₄: Only use the temperature degradation data

5) M₅: Only use the discharge voltage degradation data

Note that if lifetime data are not incorporated in a model, we cannot get the estimation of parameter θ₂ in Copula function C₂(·) in Eq. (15), which is used to model the joint distributions of reliability and RUL. Therefore, in model comparison, we will not take account of the model only based on degradation data of two PCs with dependency, concerning its uselessness in further analysis of reliability and RUL.

Figure 2 Simulated degradation data of temperature (a) and discharge voltage (b) of third RLB

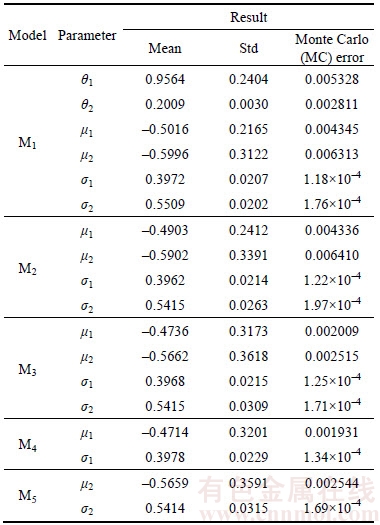
Model parameter estimation can be obtained via Bayesian MCMC method. We use WinBUGS to implement MCMC simulation. It was observed that an independent sample could be obtained by running the MCMC simulation with the sampling interval equal to 20, which means that WinBUGS will generate 20×s iterations but will store only the last one in every sequence of 20 iterations [32]. And Markov chains could be stable after 20000 iterations. So, for every model M_i (i=1, …, 5), we generated 50000 realizations of unknown parameter vector from the posterior distribution and used the last 30000 to estimate the mean, standard deviation (Std) and Monte Carlo (MC) error. Table 1 displays the results. The estimated mean values of unknown parameters will be used to calculate the reliability and predict RUL for comparison in the following parts. The standard deviation is a measure that is used to quantify the amount of variation or dispersion of estimates. What’s more, in the analysis of the MCMC output, MC error is also an important measure, which measures the variability of each estimate due to the simulation. MC error must be low in order to calculate the parameter of interest with increased precision [32]. From Table 1, we observe that the Std and MC error of M₁’s results are smaller than others, which indicates the higher precision of the results.

Table 1 Parameter estimation results of five models

4.1.3 Model selection

Then we used deviance information criterion (DIC) to draw a comparison of five models. DIC was developed by SPIEGELHALTER et al [37, 38], which is typically used as a measure in model comparison and selection [24, 39]. Particularly, it is useful in Bayesian model selection problems where the posterior distributions of the models are obtained by MCMC method.

To calculate the DIC of a model, we introduce some definitions in advance. The first is Bayesian deviance expressed as

                  (28)

where y represents the data, and θ is the vector of unknown parameters of the likelihood p(y|θ); A is a constant that can be canceled out in the comparison of all the models. So, we do not need to know its value. Define the posterior mean deviance as

                            (29)

which can be taken as a Bayesian measure of fitness or adequacy. Then an information theoretic argument is used to motivate a complexity measure p_D for the effective number of free parameters in the model expressed as

                          (30)

where 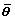is the expectation of the parameter vector θ. The complexity measure p_D indicates the difference between the posterior mean of the deviance and the deviance at the posterior estimates of the parameters of interest.

It is known that the good fitness always results in the increase of complexity. An appropriate model should trade off the two quantities well. Therefore, SPIEGELHALTER et al [37] suggested that the adequacy and complexity p_D may be added to form a DIC for model comparison. The deviance information criterion DIC is given by

                       (31)

Note that the values of DIC can be negative [40] and smaller value of DIC indicates better model.

The results are shown in Table 2. From Table 2, we observe that the model M₁ synthesizing the dependent bivariate degradation and failure lifetime data has the smallest DIC, indicating the best-fitted model. Thus, M₁ may be the best choice to model the degradation process and to do further research on reliability and RUL.

Table 2 DIC of five models

4.1.4 Reliability evaluation and RUL prediction

After obtaining parameter estimation, we can use the models in sections 2.2 and 2.3 to conduct reliability evaluation and real-time RUL prediction of the satellite RLB. Figure 3 shows the comparison of reliability evaluation results using five models. And Figure 4 shows the five different failure PDFs.

Then we uniformly select 2000 sample points in the interval [0, 20] from each reliability curve, and use the sum of squared errors (SSE) to check the goodness-of-fit for each model. The SSE of model M_i is

where r_i,j is the reliability sampled from M_i, and R_j is the actual reliability at the sampling time j. The same operation is also carried out on the failure PDFs. The SSEs of reliability curves and failure PDFs from each model are listed in Table 3. The results demonstrate that M₁ has the smallest SSE, indicating the best goodness-of-fit.

Figure 3 Comparison of satellite RLB’s reliability obtained from 5 different models

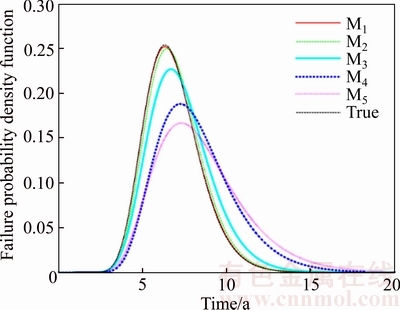
Figure 4 Comparison of failure probability density functions obtained from 5 different models

Table 3 SSE of each reliability curve

We can see the differences between models from Figures 3 and 4. When only concerning degradation of a separate PC (M₄ and M₅), the reliability is much higher than simultaneously considering bivariate PCs (M₁, M₂ and M₃), which implies that a single PC cannot depict the condition of the RLB in the general. Furthermore, the reason that reliability obtained from M₃ is higher than that from M₁ and M₂ is because we just take into consideration of two PCs, but there might be other failure factors (such as current, capacity) and we did not consider but acting upon the RLB’s healthy condition. However, in combination with the lifetime data, we can remedy the weakness to some extent. From Table 1, we can see that obvious differences mainly exist in the estimates of drift parameters μ₁ and μ₂ from five models and the estimated mean values of μ₁ and μ₂ obtained from M₁ and M₂ are much closer to the real values than those from another three models. In addition, when lifetime data are not incorporated (M₃, M₄ and M₅), the estimated results of drift parameters are similar. However, the estimates of σ₁ and σ₂ in five models all highly approximate to the real values. In addition, Figures 3 and 4 also demonstrate that models (M₁ and M₂) synthesizing the degradation and lifetime data simultaneously perform better than others. Thus, we deduced that the failure lifetime data have a great influence on drift parameters μ₁ and μ₂, which control the degradation rate and directly affect the reliability and RUL. Therefore, failure lifetime data fusion is necessary, and they can effectively revise the model parameters. Further, the discrepancy between M₁ and M₂ is caused by whether considering the dependency of the two PCs modeled via Copula function. In reality, the temperature and discharge voltage are closely related. Ignoring the relationship between them might decrease the accuracy of the model to some extent.

According to the results in Table 1, the distribution of RUL can be obtained. Table 4 tablets the results of expected RUL predicted by five models at five measurement times (respectively 1, 2, 3, 4 and 5 year). From Table 4, we can see that the overall trend of real-time RUL declines as time increases. The graphical RUL prediction results of the satellite RLB using model M₁ are shown in Figure 5. It shows that the actual RUL falls within the range of the RUL distribution at each prediction time and the scale of the RUL distribution narrows with the degradation sample size increasing. Thus, the precision of the estimated RUL is gradually improved.

Table 4 Comparison of prediction results of RUL

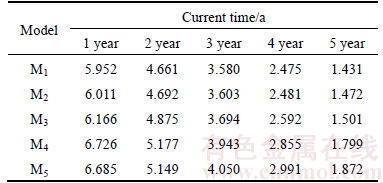
Figure 5 Graphical results of RUL prediction based on model M₁

Moreover, we study the relative error of prediction results with respect to the five models. The relative error of model M_i at measurement time t_j is defined as

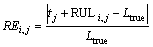                 (32)

where RUL_i,j is the predicted RUL of model M_i at current time t_j, and L_true represents the true overall lifetime of the third RLB. Figure 6 shows the graphic results of the relative errors of five models at five different measurement times. Approximately, the relative errors decrease while more degradation data are used to predict the RUL. It is remarkable that the prediction results obtained from model M₁ are more precise than that from other models. Further, it merits attention that lines of M₃, M₄ and M₅ show a slightly upward trend between the third and the fourth year. This is since the degradation rates of the two simulated degradation processes are little slower than before. Whereas, lines of M₁ and M₂ just slow down the decreasing rate. Therefore, synthesizing the lifetime data (M₁ and M₂) can reduce the influence of this period.

Figure 6 Relative errors of predicted RUL of five models

4.2 A practical case study

In this subsection, we apply the proposed Bayesian framework to a real project to verify the usability of the model. In this project, a communication satellite has been working on orbit for approximate 2 year. A real-time monitoring system is used to monitor the status and collect performance data of a RLB in its electrical power system. Data collection includes PC’s name, degradation value, monitoring time and the real- time environmental stress. However, only temperature and discharge voltage of the RLB were monitored during the satellite’s operation period. In the monitor system, there is a temperature measurement point on the RLB to collect the temperature data, and a sensor to monitor its discharge voltage. In addition, we have several lifetime data of other satellites working in the similar environment. The aim is to take full advantage of the limited data to predict RUL of the RLB for prognostic and health management.

Figure 7 shows the 150 groups of temperature and discharge voltage degradation data within 1.5 year of the satellite RLB and the measurements are taken at the same measurement times. The failure thresholds of two PCs are also respectively ω₁=1.5 °C, ω₂=45 V. Besides, two items of failure lifetime data are respectively ξ₁=6.29 year, ξ₂=6.11 year.

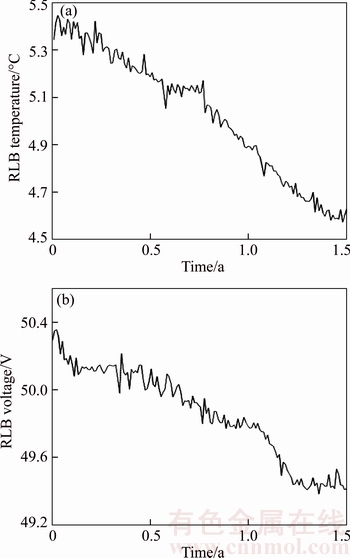
Figure 7 Original data taken from a real project

4.2.1 Linear Wiener model identification

There are many different degradation models, such as Wiener process and Gamma process. Model mis-specification probably leads to different reliability assessment results [41]. To ensure that the single degradation process can be described by linear Wiener process, first we should check the model’s applicability. To ensure that each of PC can be governed by a linear Wiener process, normality test of degradation increments is conducted. Let 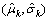be the estimation of 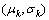for k=1, 2. According to the property of Wiener process, the observed degradation increments Δx_k(t_i) follow normal distribution denoted as

                  (33)

Thus, the inverse function of normal distribution function can be expressed in a linear function of Δx_k(t_i),

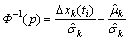                    (34)

where Φ^–1(·) denotes the inverse function of normal CDF and Φ^–1(p) represents p-quantile. Here, we use the normal probability plot to graphically assess whether the degradation increments could come from a normal distribution. If the data are normal, the plot will be approximately linear. Otherwise, it implies poor fit, and other degradation models should be considered. The graphic results shown in Figure 8 indicate a good fit and the two PCs can be governed by linear Wiener processes. In addition, other quantitative methods such as Kolmogorov- Smirnov Test [42] can also be adopted to check model and the quantitative test results also show the validity of the Wiener process model.

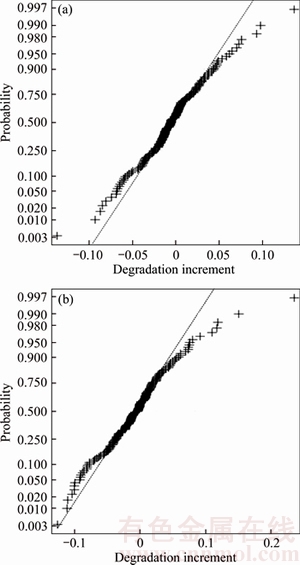
Figure 8 Normal probability of two PCs

4.2.2 Model application

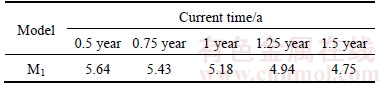
The estimates of unknown parameters of the proposed model M₁ are obtained by MCMC algorithm, as listed in Table 5. The corresponding RUL prediction results are listed in Table 6. Observing Table 6, it is worth noting that the RUL loss between 1.25 and 1.5 year is quite small, just 0.14 year. However, observing the original degradation data of discharge voltage drawn in Figure 7, this abnormal phenomenon can be explained. We can see that the tail of discharging voltage degradation data (approximately the last 30 odds) presents a little different downward trend with lower decreasing rate. So, the estimate of negative diffusion parameter μ₂ based on 125 groups of discharging voltage data is smaller than that based on 150 samples. Thus, the predicted RUL results in the last two columns in Table 6 are accountable. According to the RUL loss between two years, it shows the validity of the model.

Table 5 Parameter estimation of M₁ using data from a real project

Table 6 RUL prediction results of real satellite RLB

5 Conclusions

A Bayesian framework was put forward for RUL prediction and reliability analysis of a satellite RLB by synthesizing bivariate degradation and lifetime data. Frank Copula function was used to characterize the dependency of two PCs (temperature and voltage) of the RLB. A simulation study illustrated the effectiveness and validity of our model. The results showed that the reliability evaluation and RUL estimation were too risky if only considering a single PC or considering the two PCs to be independent. And the fusion of bivariate degradation and lifetime data could obtain more accurate results. This bivariate degradation model can be applied to general linear Wiener process via incorporating lifetime data, without assuming the process to be monotonous. The model is also applicable to non-linear Wiener process with time-scale transformation. In addition, the RLB Bayesian model can account for on-orbit temperature and discharge voltage, as well as the lifetime data of congeneric RLBs. Whereas, temperature and discharge voltage are just taken for example to be the health indicators. In general, it is noted that the model is applicable to other RLBs characterized by some different two PCs because there are no specific assumptions of the battery or two PCs. Finally, the real-time RUL prediction can provide essential information for prognostics and healthy management of RLBs to prevent catastrophic failure of long-life satellites. However, the degradation mechanisms of a RLB are far more complex than we considered in this paper. Degradation model based on more than two PCs as well as failure physics can be studied in the future.

Appendix

Algorithm to simulate bivariate Wiener degradation process:

Step 1: Set initial values (X₁(t₀), X₂(t₀)), t₀=0 and Δt.

Step 2: Simulate degradation increments of two PCs.

1) Generate two independent variables (u, s) from uniform (0, 1);

2) Set where denotes the quasi-inverse of C_u(·):

3) Set degradation increments ΔX₁(t_i) and ΔX₂(t_i) with

where Φ^–1(·) is the quasi-inverse of Φ(·), and t_i=t_i–1+Δt.

Step 3: Obtain degradation measurements of two PCs at time t_i with X₁(t_i)=X₁(t_i–1)+ΔX₁(t_i) and X₂(t_i)=X₂(t_i–1)+ΔX₂(t_i). If X_k(t_i)≥ω_k, set the failure time with t_i and terminate the simulation process. Otherwise, i=i+1, and go to Step 2.

References

[1] GAO Li-jun, LIU Sheng-yi, DOUGAL R A. Dynamic lithium-ion battery model for system simulation [J]. IEEE Transactions on Components and Packaging Technologies, 2002, 25(3): 495–505.

[2] ERDINC O, VURAL B, UZUNOGLU M. A dynamic lithium-ion battery model considering the effects of temperature and capacity fading [C]// International Conference on Clean Electrical Power. Capri, Italy: IEEE, 2009: 383–386.

[3] JIN Guang, MATTHEWS D E, ZHOU Zhong-bao. A Bayesian framework for on-line degradation assessment and residual life prediction of secondary batteries in spacecraft [J]. Reliability Engineering & System Safety, 2013, 113: 7–20.

[4] PATEL M R. Spacecraft power systems [M]. Boca Raton: CRC Press, 2005.

[5] SI Xiao-sheng. An adaptive prognostic approach via nonlinear degradation modelling: Application to battery data [J]. IEEE Transactions on Industrial Electronics, 2014, 62(8): 5082–5096.

[6] TANG Sheng-jin, YU Chuan-qiang, WANG Xue, et al. Remaining useful life prediction of lithium-ion batteries based on the Wiener process with measurement error [J]. Energies, 2014, 7(2): 520–547.

[7] HU Chao, JAIN G, TAMIRISA P, et al. Method for estimating capacity and predicting remaining useful life of lithium-ion battery [J]. Applied Energy, 2014, 126: 182–189.

[8] SONG L, EVANS J W. Electrochemical-thermal model of lithium polymer batteries [J]. Journal of the Electrochemical Society, 2000, 147(6): 2086–2095.

[9] GU W B, WANG C Y. Thermal-electrochemical modeling of battery systems [J]. Journal of the Electrochemical Society, 2000, 147(8): 2910–2922.

[10] LIAW B Y, JUNGST R G, NAGASUBRAMANIAN G, et al. Modeling capacity fade in lithium-ion cells [J]. Journal of Power Sources, 2005, 140(1): 157–161.

[11] SHIM J, KOSTECKI R, RICHARDSON T, et al. Electrochemical analysis for cycle performance and capacity fading of a lithium-ion battery cycled at elevated temperature [J]. Journal of Power Sources, 2002, 112(1): 222–230.

[12] SPOTNITZ R. Simulation of capacity fade in lithium-ion batteries [J]. Journal of Power Sources, 2003, 113(1): 72–80.

[13] LIU Da-tong, WANG Hong, PENG Yu, et al. Satellite lithium-ion battery remaining cycle life prediction with novel indirect health indicator extraction [J]. Energies, 2013, 6(8): 3654–3668.

[14] VETTER J, NOV K P, WAGNER M R, et al. Ageing mechanisms in lithium-ion batteries [J]. Journal of Power Sources, 2005, 147(1): 269–281.

[15] WANG Xiao-lin, GUO Bo, CHENG Zhi-jun. Residual life estimation based on bivariate Wiener degradation process with time-scale transformations [J]. Journal of Statistical Computation and Simulation, 2012, 84(3): 545–563.

[16] CHEN S C, WAN C C, WANG Y Y. Thermal analysis of lithium-ion batteries [J]. Journal of Power Sources, 2005, 140(1): 11–24.

[17] ZHANG Jing-liang, LEE J. A review on prognostics and health monitoring of Li-ion battery [J]. Journal of Power Sources, 2011, 196(15): 6007–6014.

[18] CHOI Young-jin, WANG Jin-suk. Stability analysis of a voltage-temperature (V/T) limit circuit for satellite power system [C]// Proceedings of the Energy Conversion Engineering Conference (IECEC 1996). Washington, DC, USA: IEEE, 1996, 1: 316–321.

[19] COX D R, MILLER H D. The theory of stochastic process [M]. London: Chapman and Hall, 1965.

[20] PAN Zheng-qiang, BALAKRISHNAN N, SUN Q, et al. Bivariate degradation analysis of products based on Wiener processes and copulas [J]. Journal of Statistical Computation and Simulation, 2013, 83(7): 1316–1329.

[21] WANG Xiao-lin, GUO Bo, CHENG Zhi-jun, et al. Residual life estimation based on bivariate Wiener degradation process with measurement errors [J]. Journal of Central South University, 2013, 20(1): 844–851.

[22] SAHA B, GOEBEL K, POLL S, et al. Prognostics methods for battery health monitoring using a Bayesian framework [J]. IEEE Transactions on Instrumentation and Measurement, 2009, 58(2): 291–296.

[23] HE Wei, WILLIARD N, OSTERMAN M, et al. Prognostics of lithium-ion batteries based on Dempster–Shafer theory and the Bayesian Monte Carlo method [J]. Journal of Power Sources, 2011, 196(23): 10314–10321.

[24] WANG Li-zhi, PAN Rong, LI Xiao-yang, et al. A Bayesian reliability evaluation method with integrated accelerated degradation testing and field information [J]. Reliability Engineering & System Safety, 2013, 112: 38–47.

[25] LEHMANN A. Joint modeling of degradation and failure time data [J]. Journal of Statistical Planning and Inference, 2009, 139(5): 1693–1706.

[26] GUO Ji-qiang, WILSON A G. Bayesian methods for estimating system reliability using heterogeneous multilevel information [J]. Technometrics, 2013, 55(4): 461–472.

[27] NELSEN R B. An introduction to copulas [M]. Second ed. New York: Springer Science+Business Media, Inc, 2006.

[28] PENG Wei-wen, HUANG Hong-zhong, LI Yan-feng, et al. Life cycle reliability assessment of new products—A Bayesian model updating approach [J]. Reliability Engineering & System Safety, 2013, 112(10): 9–19.

[29] SKLAR A. Random variables, joint distributions, and copulas [J]. Kybernetica, 1973, 9(6): 449–460.

[30] SAHA B, GOEBEL K. Modeling Li-ion battery capacity depletion in a particle filtering framework [C]// The Annual Conference of the Prognostics and Health Management Society. San Diego, CA: PHMsociety, 2009: 2909–2924.

[31] PENG C Y, TSENG S T. Mis-specification analysis of linear prediction models [J]. IEEE Transactions on Reliability, 2009, 58(3): 444–455.

[32] NTZOUFRAS I. Bayesian modeling using WinBUGS [M]. Canada: John Wiley & Sons, Inc, 2009.

[33] PENG Wei-wen, LIU Yu, LI Yan-feng, et al. A Bayesian optimal design for degradation tests based on the inverse Gaussian process [J]. Journal of Mechanical Science and Technology, 2014, 28(10): 3937–3946.

[34] WANG Zhong-lai, HUANG Hong-zhong, DU Li. Reliability analysis on competitive failure processes under fuzzy degradation data [J]. Applied Soft Computing, 2011, 11(3): 2964–2973.

[35] YUAN T, JI Y. A Hierarchical bayesian degradation model for heterogeneous data [J]. IEEE Transactions on Reliability, 2015, 64(1): 63–70.

[36] PAN Zheng-qiang, BALAKRISHNAN N, SUN Quan. Bivariate constant-stress accelerated degradation model and inference [J]. Communications in Statistics-Simulation and Computation, 2010, 40(2): 247–257.

[37] SPIEGELHALTER D J, BEST N G, CARLIN B P, et al. Bayesian measures of model complexity and fit [J]. Journal of the Royal Statistical Society, 2002, 64(4): 583–639.

[38] SPIEGELHALTER D J, BEST N G, CARLIN B P, et al. The deviance information criterion: 12 years on [J]. Journal of the Royal Statistical Society: Series B, 2014, 76(3): 485–493.

[39] HAO Hui-bing, SU Chun. A Bayesian framework for reliability assessment via wiener process and MCMC [J]. Mathematical Problems in Engineering, 2014, 2014 Article ID 486368. DOI: 101155120141486368.

[40] SANTOS C A, ACHCAR J A. A Bayesian analysis in the presence of covariates for multivariate survival data: An example of application [J]. Revista Colombinana De Estadistica, 2011, 34(1): 111–131.

[41] TSAI C C, TSENG S T, BALAKRISHNAN N. Mis-specification analyses of gamma and Wiener degradation processes [J]. Journal of Statistical Planning and Inference, 2011, 141(12): 3725–3735.

[42] MASSEY J R, FRANK J. The Kolmogorov-Smirnov test for goodness of fit [J]. Journal of the American Statistical Association, 1951, 46(253): 68–78.

(Edited by YANG Hua)

中文导读

卫星蓄电池二元性能退化和寿命数据的贝叶斯模型

摘要：卫星蓄电池剩余剩余寿命预测是卫星系统故障诊断与健康管理的重要一环。本文创新性的提出了一个融合二元性能退化数据和寿命数据的可靠性分析贝叶斯模型，对卫星锂电池的剩余寿命进行预测。二元性能退化是指系统存在两个相关的性能退化现象，二者的共同作用下可能导致系统故障。模型中首先利用Copula函数和线性维纳过程对锂电池的二元性能退化数据进行建模。而后，利用贝叶斯模型融合小子样寿命数据，采用马尔科夫蒙特卡洛仿真估计模型参数，从而对剩余寿命进行预测，并通过仿真和实例分析对所提模型的性能进行分析。结果表明融合了二元性能退化数据和寿命数据后，剩余寿命的预测精度能够有效提高。

关键词：可充电锂电池；贝叶斯柜架；二元性能退化；寿命数据；剩余寿命；可靠性分析

Foundation item: Project(71371182) supported by the National Natural Science Foundation of China

Received date: 2015-10-09; Accepted date: 2017-10-12

Corresponding author: ZHANG Yang, PhD Candidate; Tel: +86–731–84573550; E-mail: sunnyyzhang1992@163.com: ORCID: 0000- 0003-1524-385X