Trans. Nonferrous Met. Soc. China 24(2014) 1690-1697

Precipitation kinetics of NZ30K-Mg alloys based on electrical resistivity measurement

Xiao-na WANG, Li-zhan HAN, Jian-feng GU

Shanghai Key Laboratory of Materials Laser Processing and Modification, School of Materials Science and Engineering, Shanghai Jiao Tong University, Shanghai 200240, China

Received 24 June 2013; accepted 9 August 2013

Abstract: The electrical resistivity of NZ30K-Mg alloy was measured at different heating rates during continuous heating to study the precipitation kinetics. Two kinds of metastable phases, β″ and β′, formed during the heating. Kissinger method and differential isoconversional method were employed to assess the precipitation kinetic parameters of NZ30K-Mg alloy, activation energy E_α and pre-exponential factor 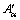. The fraction of transformation (α) and the precipitation sequence in NZ30K-Mg alloy were determined. Continuous heating transformation (CHT) and isothermal heating transformation (IHT) diagrams were further obtained for guiding the aging of NZ30K-Mg alloy. The analysis shows that the precipitation kinetic parameters of NZ30K-Mg alloy can be obtained accurately using isoconversional method.

Key words: NZ30K-Mg alloy; precipitation kinetics; differential isoconversional method; continuous heating transformation; isothermal heating transformation

1 Introduction

Magnesium alloys are widely used in automotive, aeronautical, electrical and electronic products due to their low density and high specific strength [1,2]. However, the conventional magnesium alloys are only suitable for low-temperature application (≤523 K) as their mechanical properties deteriorate at elevated temperatures [3,4]. The addition of rare-earth (RE) elements can effectively enhance the properties, such as the room- and high-temperature strength, creep, heat and corrosion resistance. This allows magnesium alloys to be used in many more areas [2,5-7]. It is found that age-hardening response is prominent in these alloys and is a key factor to achieve the desired properties. Therefore, the age-hardening response and precipitation sequence of a wide range of Mg-RE alloys have been studied recently [7-12].

Four different precipitation phases, leading to complex microstructure and further improving the properties, were found in the ageing process of Mg-RE alloys [1,2,9,11-15]. The four different precipitations, denoted as β″(DO₁₉), β′(CO), β₁(FCC) and β(BCT), were proposed with stoichiometry of Mg₃RE, Mg₅RE, Mg₃RE and Mg₃RE. For Mg-Gd alloys [14,16], the precipitations were β″ and/or β′. In the alloys with the addition of Y, such as WE54 and WE43, all of the four precipitation phases were observed. For Mg-Nd alloys, the materials of interest, three kinds of precipitation phases have been reported: β″ (a=b=0.64 nm, c=0.52 nm), β′(a=0.736 nm) and the equilibrium phase β (a=1.03 nm, c=0.593 nm) [8].

Various experimental methods, such as hardness, calorimetry, X-ray diffraction and TEM [17-21], have been used to analyze the phase transformation and microstructure in the aging process. For Mg-Nd alloys, it was found that the precipitation sequence [8,22,23] is as follows: supersaturated solution→G. P. zones →β″→β′→β. G. P. zones are in fact a form of disc on 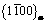planes of α-Mg. β″ with disc shape, is completely coherent with the matrix, and obeys the relationship of (0001)_β″//(0001)_Mg, 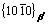//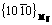. β″ is a stable phase within a wide temperature range and contributes to the peak of age hardening. β′ phase is semi-coherent with the matrix [8,13]. There is no coherent relationship between the matrix and the equilibrium phase β.

The precipitation fraction influences the mechanical properties of Mg-Nd alloys significantly, so it is important to know the kinetic process of precipitation. To determine the kinetic parameters of precipitation, various techniques have been used, such as differential scanning calorimetry (DSC), hardness measurement, and electrical resistivity measurement [18,20,24]. In this research, resistivity measurement is used for qualitative description of phase transformation in magnesium alloy. This technique has been extensively used to analyze the precipitation kinetics because it not only can measure properties at macroscopic scale but also is sensitive to atomic-scale phenomena [25-27].

However, to our knowledge, no quantitative attempt has been made to analyze the precipitation kinetics of NZ30K-Mg alloy. The principle objective of this research is to determine the precipitation kinetic parameters and the continuous heating transformation (CHT) and isothermal heating transformation (IHT) diagrams of NZ30K-Mg alloy, so as to establish the relationships of the heating rate, the extent of conversion and the time, which are valuable to guide the ageing process of NZ30K-Mg alloy.

2 Experimental

The material used in this research was NZ30K (Mg-3.0Nd-0.2Zn-Zr, mass fraction, %) magnesium alloy. It was prepared from pure Mg, Zn, Mg-Nd alloy and Mg-Zr alloy in an electrical resistance crucible under the protection of the SF₆/CO₂ flux. Solution heat treatment was performed in an air resistance furnace at 813 K for 4-10 h under the protection of SO₂ decomposed from pyrites. The specimens were then quenched in the air.

The aging of air-quenched specimens was performed in an electrical resistance furnace at various temperatures in nitrogen gas. The dimension of the samples was 30 mm × 8 mm × 2 mm and their oxide layers were removed before aging.

The four-point probe method was adopted to measure the electrical resistance during the aging process, using a rig designed by ourselves. Figure 1 shows the schematic of the electrical system. The apparatus consisted of heating chamber, heating system, experimental data acquisition and processing system. A constant current of 1.5 A was applied to the sample during the process, and the voltage was recorded. The electrical resistance was converted from the voltage changes measured. The resistance, R, was used to calculate the resistivity (ρ) as follows:

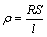                                    (1)

where S is the cross sectional area of the sample, and l is the constant distance between the two potential probes. The time step of the data collecting system was set to be 1.7 s to accumulate large enough data sets, in order to minimize the systematic errors.

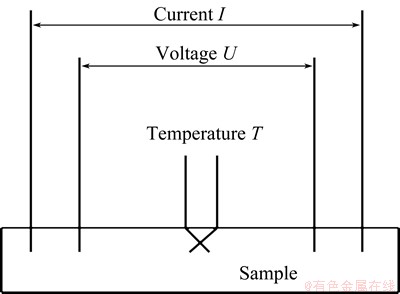
Fig. 1 Schematic of electrical resistivity measurement rig

During the continuous heating, the samples were heated at a fixed heating rate until the phase transformation had finished. The heating rates of 0.10, 0.17, 0.55, 1.08, 2.30, 5.90 and 7.25 K/min were adopted in the experiment, and the schematic diagram of experimental conditions is shown in Fig. 2.

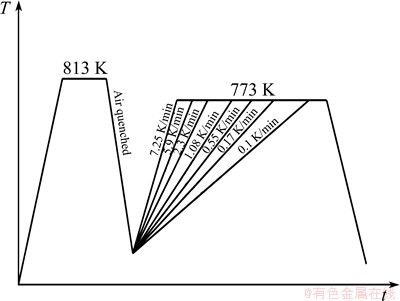
Fig. 2 Schematic diagram of experimental conditions

3 Results

The electrical resistivity revolution during continuous ageing at different heating rates is shown in Fig. 3. It can be found that two inflections (Fig. 3) exist on these curves, which in fact indicate the precipitation of β″ and β′. The inflection points move to higher temperatures with increasing of the heating rate, suggesting the thermally activated nature of the transformation. In addition, as the heating rate increases, the inflection of β″ becomes less obvious while that of β′ becomes more prominent, indicating that the precipitation fraction of β″ decreases while that of β′ increases. When the transformation finishes, the electrical resistivity varies with temperature for different heating rates, indicating that the total amount of precipitation during continuous heating at various heating rates is almost the same.

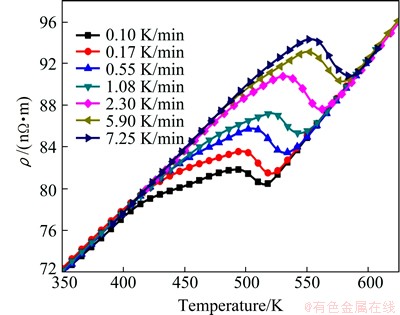
Fig. 3 Electrical resistivity evolution in continuous heating with different heating rates

As the electrical resistivity suggests the accumulated precipitation in the alloy, its differential curve displays the change of the precipitation rate (Fig. 4). The two peaks in each curve correspond to the maximum transformation rates of metastable phases β″ and β′, respectively. Overlap of β″ and β′ peaks occurs, especially at higher heating rates. Both peak transformation temperatures of the two phases increase with heating rates. The area under β″ reaction peak (the amount of β″) is much smaller than that of β′, and is significantly reduced at higher heating rate. From Fig. 4, peak temperatures of phase transformation of β″ and β′ are listed in Table 1.

Fig. 4 Differential curves of electrical resistivity

Table 1 Peak temperatures of phase transformation in NZ30K- Mg alloy at different heating rates

According to the basic theories of the electrical resistivity [28], all factors that tend to disrupt the regularity of the metal lattice are possible to increase resistivity. Among these factors, the solute atoms scatter conducting electrons, hence increase the resistivity. During the aging process, solutes are depleted from the matrix, so its contribution to the resistivity is reduced as precipitation progresses. Based on Matthiessen’s law, the electrical resistivity of the solid solution, ρ, can be described as

ρ_t=ρ(T)+ρ_aC_t                                (2)

where ρ_t and C_t are the resistivity of the solid solution and the concentration of solute in the matrix at time t, respectively; ρ_a is the solute coefficient; ρ(T) is the resistivity of the pure Mg, which is assumed to be constant at certain experimental temperature. Therefore, the change of resistivity during aging is proportional to the change in the solute concentration. In the aging process of NZ30K-Mg alloy, the decrease of Nd solute concentration is proportional to the precipitate fraction. Thus, the reacted fraction at a given heating rate can be expressed according to the resistivity of the alloy:

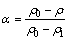                                 (3)

where ρ₀, ρ and ρ₁ are the electrical resistivity of the alloy before, during and after transformation, respectively.

Using the data shown in Fig. 3 and Eq. (3), the conversional curves of the precipitation at different heating rates are calculated and the results are shown in Fig. 5. The curve of transformation fraction versus temperature is sigmoidal in shape, and moves to higher temperature with increasing of the heating rate, suggesting that the metastable phase formation is kinetically driven. The precipitation curves can be divided into two parts, each corresponding to the formation of β″ and β′, respectively. The sum of two metastable phases fraction equals 1. With increasing of the heating rate, the length of the first part decreases while that of the second increases, indicating the fraction of β″ decreases and that of β′ increases. At the beginning of the heating, β″ is only the precipitation phase. As the temperature increases, β′ emerges due to the transformation of β″ to β′ and the precipitation of β′ from the matrix directly. After β″ is consumed, only β′ precipitates from the matrix and grows continuously.

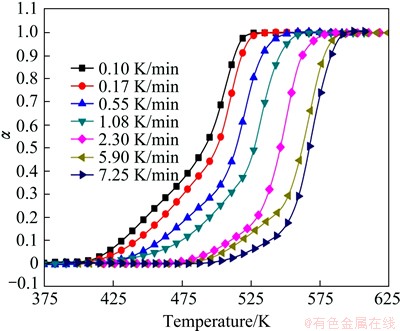
Fig. 5 Precipitation fraction at different heating rates

4 Analysis

There are several methods to study the precipitation kinetics and determine the activation energies associated with the precipitation and dissolution process [19,20,29,30]. In this work, two models, Kissinger model (KM) [29] and isoconversional model (IM) [30,31], were applied.

The KM is based on the fact that the peak temperature (T_p) depends on the heating rate (Φ). The effective energy can be determined from the Kissinger equation:

                     (4)

where T_p is the peak temperature; Φ is the heating rate; E is the activation energy; R is the molar gas constant; and K₀ is the pre-exponential factor of Arrhenius.

Using the data summarized in Table 1, E and K₀ can be obtained from the plot of 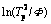 versus 1/RT_p (Fig. 6). The calculated activation energy, which is assumed to be constant in KM, is 142.33 kJ/mol for β′ and 85.13 kJ/mol for β″, respectively. The effective precipitation energy of β″ is much smaller than that of β′.

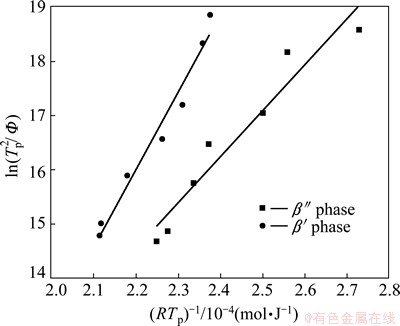
Fig. 6 Kissinger plot of β″ and β′ precipitation peak temperatures for NZ30K-Mg alloy

Another model to determine the precipitation kinetic parameters is the isoconversional model, in which the reaction rate is assumed to be a function of only two variables, T and α. The usual relationship can be expressed as

                            (5)

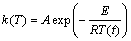                      (6)

where α is the conversional fraction. Isoconversional model can determine the kinetic parameters without the knowledge of detailed reaction and can describe the processes of parallel or consecutive steps precisely. The isoconversional methods obey the isoconversional principle: the reaction rate at a certain level of conversion is only a function of temperature. It can be expressed by taking the logarithmic derivative of Eq. (5) as follows:

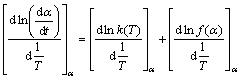      (7)

Because f(α) is the constant for the fixed α, the second term in the right hand side of Eq. (7) is zero. Combining Eq. (7) and the logarithmic derivation of Eq. (6) reduces to the expression as follows:

                         (8)

Then the activation energy E_α can be evaluated. Differential isoconversional method (DIM) is usually more accurate than the integral method, and the most commonly used Friedman [32] differential isoconversional method is proposed as follows:

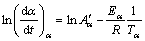                     (9)

                               (10)

where t, T_α, E_α and A_α are the time, temperature, apparent activation energy and pre-exponential factor at conversion α, respectively. –E_α/R and 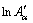 are the slope and the intercept with the vertical axis of the plot of ln(dα/dt)_α versus 1/T_α. For linear nonisothermal program with heating rate Φ, Eq. (9) is usually used in the following form:

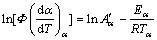                   (11)

The value of effective activation energy E_α is required as a necessary input for analyzing precipitation kinetics, which could be fitted using the experimental data. The energy value associated with a particular step cannot be determined accurately due to the complexity of the precipitation reactions, so the effective kinetic parameters are the value composed of the intrinsic kinetic parameters of many individual steps. Valid values of the precipitation kinetic parameters can be obtained through the DIM mentioned above, without dividing particular steps in the transformation [30,31]. The value of E_α has been obtained as a function of the conversion through Eq. (11). f(α) is a constant at any fixed value of α. In each temperature program, the isoconversional rate and the temperature are obtained for a fixed α. Considering α=0.1, α=0.3 and α=0.6, at the point in each experiment when α=0.1, α=0.3 and α=0.6, the corresponding isoconversional rate and temperature are measured. The Arrhenius plots of the instantaneous rate are shown in Fig. 7, from which E_0.1, E_0.3 and E_0.6 are obtained from the slopes, respectively. One can establish the temperature dependence of the isoconversional reaction rate using a limited but sufficiently diverse set of small scale experiments. This can be used to evaluate the values of the activation energy E_α and a modified pre-exponential factor 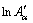 without explicitly assuming a particular form of the reaction model f(α). The two parameters are determined within a wide range of 0.05-0.95 for α, the variations of E_α and  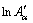with the precipitation fraction of NZ30K-Mg alloys is shown in Fig. 8. One could observe a significant variation of E_α and 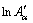with respect to α, which indicates a kinetically complex process.

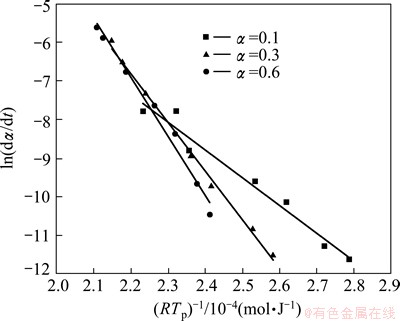
Fig. 7 Arrhenius plots at different heating rates when α=0.1, α=0.3 and α=0.6

Activation energy variation is characterized with two plateaus (Fig. 8). E_α remains almost unchanged when α is below 0.1 and above 0.6. However, the activation energy increases greatly when α is in the range of 0.1 to 0.4, until it reaches the second plateau. Based on the precipitation sequence and the kinetics analysis by Kissinger method, the two plateaus are interpreted as stable precipitation of β″ and β′, respectively. The activation energies of β″ (71.5 kJ/mol) and β′ (149.6 kJ/mol) are estimated from the two plateaus.

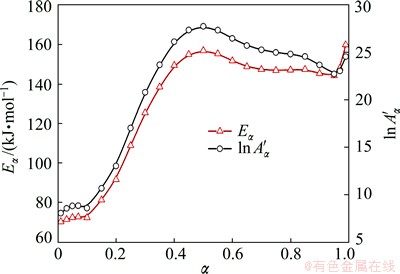
Fig. 8 Activation energy and pre-exponential factor as function of precipitation fraction

When β″ starts to transform into β′, E_α is the activation energy of β″ transforming to β′ and β′ precipitating from matrix. The activation energy increases until it totally steps into the β′ precipitation process.

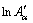shows a similar trend as the effective energy. When the transformation faction is below 0.1, it remains almost the same, at the value of 80, then increases gradually with the increasing conversion and finally reaches 25 when the conversion rate is above 0.5.

Compared with KM, DIM gives the similar effective active energy for both precipitations, β″ and β′, indicating that the DIM has the same efficiency as the conversational KM. In addition, the DIM can display the change of the parameters during the ageing process. Therefore, the DIM is chosen to study the precipitation kinetics.

5 Discussion

5.1 Continuous precipitation kinetics

Using the kinetics parameters calculated from Eq. (11), the precipitation fraction variations can be calculated as follows:

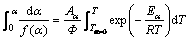              (12)

For infinitesimal ranges of reaction progress Δα, Eq. (12) is rewritten as

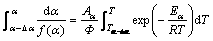          (13)

As Δα is very small, the activation energy E_α can be assumed constant. For Δα→0, the integral isoconversional method is an effective DIM method. Therefore, integral isoconversional method yields the calculated reaction fraction with the obtained parameters.

The comparison between the calculated transformation fraction curves and the experimental results at different heating rates are shown in Fig. 9. They agree particularly well in the higher temperature ranges, which corresponds to the formation of β′. This suggests that the precipitation of the metastable phases in age-hardenable magnesium alloys is well described by the Friedman differential isoconversional method in continuous heating.

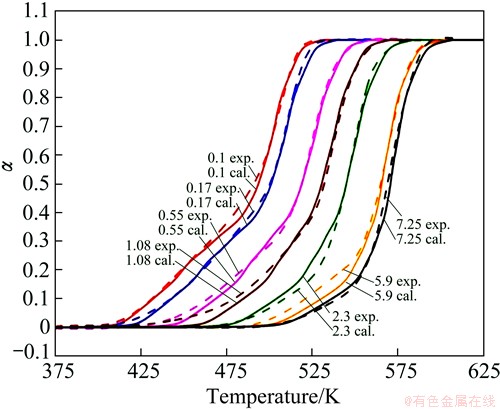
Fig. 9 Phase transformation versus temperature at a set of heating rates and calculated results with isoconversional methods for NZ30K-Mg alloy

5.2 Isothermal precipitation kinetics

From the measured electrical resistivity during the continuous heating, the time to reach a given extent of conversion under isothermal conditions (T₀) can be readily determined using the expression:

            (14)

Equation (14) can be used to predict the isothermal kinetics at any temperature, T₀, directly from the values of  and E_α in Fig. 8.

In this prediction, six temperatures from 453 to 513 K were adopted. For a fixed fraction at each temperature, the time to reach the given conversion was obtained. Then the precipitation fraction dependences of the time at different isothermal temperatures were established, as shown in Fig. 10. The curves move to right side with increasing temperature, suggesting that NZ30K-Mg alloy takes longer time to finish the precipitation process at lower temperature. This is consistent with the precipitation kinetics in continuous heating. In addition, at lower temperatures, there are two obvious inflections in the transformation curves, corresponding to precipitation of β″ and β′, respectively. The reaction rate is lower in β″ while it is higher in β′.

Fig. 10 Calculated transformation fraction curves during isothermal heating

The calculated isothermal aging curves can be validated by experiments. The electrical resistivity change in isothermal aging at 473 and 498 K are measured to test the accuracy of the calculated result in Fig. 10. The electrical resistivity and the conversion curves during isothermal aging at 473 and 498 K are shown in Fig. 11. Compared with the experimental reduced curves, it could be found that the calculated isothermal conversion curves are in good agreement with experimental results.

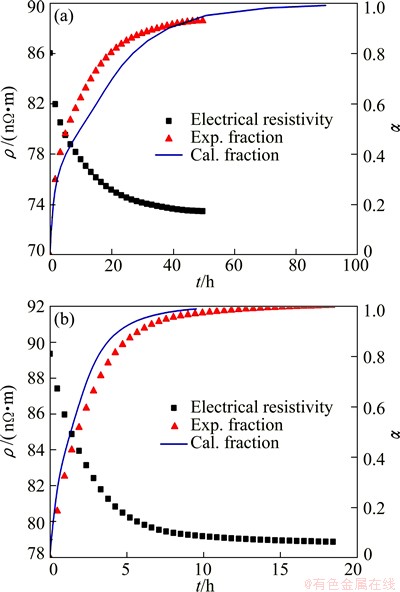
Fig. 11 Electrical resistivity and isothermal transformation curve at 473 K (a) and 498 K (b)

5.3 CHT diagram

CHT diagram of metastable phases was obtained according to the predicted results in Fig. 9. In this research, precipitation fractions of 10%, 20%, 50%, 70%, 90%, 99% were chosen for calculating the CHT diagram. For a specified heating rate, the temperature to reach the fraction α can be obtained. Then, the dependence of temperatures and heating rates for a continuously increasing precipitation fraction can be established. The temperature versus heating rate is shown in Fig. 12. The precipitation kinetics can be calculated in an arbitrary heating history from CHT diagram. In other word, one can get the information of the precipitation behavior at any heating rate or arbitrary temperature routines.

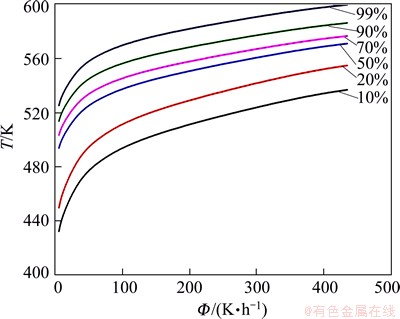
Fig. 12 CHT-diagram of NZ30K-Mg alloy

5.4 IHT diagram

IHT diagram can be obtained based on the isothermal transformation results in Fig. 10. For fixed transformation fraction α, the time to reach α at each temperature can be obtained. The time and corresponding temperature for α ranging from 10% to 99% are taken as abscissa and ordinate respectively, IHT diagram can be got (Fig. 13).

In Fig. 13, the curves move to the upper-right corner with increasing transformation fraction, which suggests that it takes for NZ30K-Mg alloys longer time to finish transformation process at lower isothermal temperatures. The precipitation kinetics at any isothermal temperature can be obtained from IHT diagram.

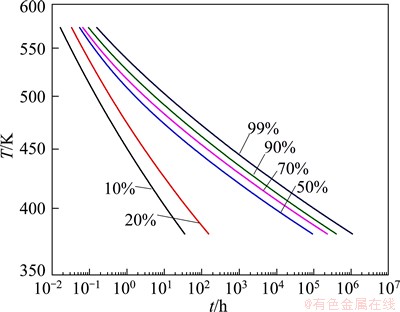
Fig. 13 IHT diagram obtained from isothermal conversion curves

6 Conclusions

1) The electrical resistivity results of NZ30K-Mg alloy measured at different heating rates exhibit two distinct precipitation behaviors: β″ precipitates at lower temperatures while β′ forms at higher temperatures. When temperature increases, β″ transforms into β′. The precipitation fraction of β′ increases as temperature rises. The reaction curves shift to higher temperatures with increasing of the heating rates.

2) Isoconversional method was used to analyze the precipitation kinetics of NZ30K-Mg alloys during continuous heating based on the electrical resistivity results, and the kinetic parameters E_α and 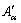 were obtained, which can be further used to calculate the precipitation fraction at any temperature and time. The transformation active energy was determined as 71.5 and 149.6 kJ/mol for β″ and β′, respectively.

3) The dependence of transformation fraction on heating rates was calculated with the obtained kinetic parameters, and the good agreement with the experimental data indicated that the precipitation kinetics of NZ30K-Mg alloys can be described using isoconversional method.

4) The precipitation fraction curves during isothermal aging were calculated from the results in continuous heating, and two of them were validated by electrical resistivity results, indicating that isothermal aging precipitation kinetics can be calculated from continuous heating precipitation kinetics.

5) CHT and IHT diagrams were established based on electrical resistivity variation during continuous heating. Therefore, the precipitation behaviors at any temperature history can be predicted to guide the aging process.

References

[1] LI J H, JIE W Q, YANG G Y. Effect of gadolinium on aged hardening behavior, microstructure and mechanical properties of Mg-Nd-Zn-Zr alloy [J]. Transactions of Nonferrous Metals Society of China, 2008, 18(S1): S27-S32.

[2] LI J H, SHA G, JIE W Q, RINGER S P. Precipitation microstructure and their strengthening effects of an Mg-2.8Nd-0.6Zn-0.4Zr alloy with a 0.2 wt.% Y addition [J]. Materials Science and Engineering A, 2012, 538: 272-280.

[3] POLMEAR I J. Recent developments in light alloys [J]. Light Alloys Metallu, 1996, 37: 12-31.

[4] ANTION C, DONNADIEU P, PERRARD F, DESCHAMPS A, TASSIN C, PISCH A. Hardening precipitation in a Mg-4Y-3RE alloy [J]. Acta Materialia, 2003, 51: 5335-5348.

[5] HANTZSCHE K, BOHLEN J, WENDT J, KAINER K U, YI S B, LETZIG D. Effect of rare earth additions on microstructure and texture development of magnesium alloy sheets [J]. Scripta Materialia, 2010, 63: 725-730.

[6] MISHRA R K, GUPTA A K, RAO P R, SACHDEV A K, KUMAR A M, LUO A A. Influence of cerium on the texture and ductility of magnesium extrusions [J]. Scripta Materialia, 2008, 59: 562-565.

[7] NUTTALL P A, PIKE T J, NOBLE B. Metallography of dilute Mg-Nd-Zn alloys [J]. Metallography, 1980, 13: 3-20.

[8] FU P H, PENG L M, JIANG H Y, CHANG J W, ZHAI C Q. Effects of heat treatments on the microstructures and mechanical properties of Mg-3Nd-0.2Zn-0.4Zr (wt.%) alloy [J]. Materials Science and Engineering A, 2008, 486: 183-192.

[9] GILL L R, LORIMER G W, LYON P. The effect of zinc and gadolinium on the precipitation sequence and quench sensitivity of four Mg-Nd-Gd alloys [J]. Advanced Engineering Materials, 2007, 9: 784-792.

[10] MA L, MISHRA R K, BALOGH M P, PENG L M, LUO A A, SACHDEV A K, DING W J. Effect of Zn on the microstructure evolution of extruded Mg-3Nd(-Zn)-Zr (wt.%) alloys [J]. Materials Science and Engineering A, 2012, 543: 12-21.

[11] NIE J F, MUDDLE B C. Characterisation of strengthening precipitate phases in a Mg-Y-Nd alloy [J]. Acta Materialia, 2000, 48: 1691-1703.

[12] NIE J F, OH-ISHI K, GAO X, HONO K. Solute segregation and precipitation in a creep-resistant Mg-Gd-Zn alloy [J]. Acta Materialia, 2008, 56: 6061-6076.

[13] PIKE T J, NOBLE B. The formation and structure of precipitates in a dilute magnesium-neodymium alloy [J]. Journal of the Less-common Metals, 1973, 30: 63-74.

[14] HONMA T, OHKUBO T, KAMADO S, HONO K. Effect of Zn additions on the age-hardening of Mg-2.0Gd-1.2Y-0.2Zr alloys [J]. Acta Materialia, 2007, 55: 4137-4150.

[15] HONMA T, OHKUBO T, HONO K, KAMADO S. Chemistry of nanoscale precipitates in Mg-2.1Gd-0.6Y-0.2Zr (at.%) alloy investigated by the atom probe technique [J]. Materials Science and Engineering A, 2005, 395: 301-306.

[16] ROKHLIN L L, NIKITINA N I. Recovery after ageing of Mg-Y and Mg-Gd alloys [J]. Journal of Alloys and Compounds, 1998, 279: 166-170.

[17] HUTCHINSON C R, NIE J F, GORSSE S. Modeling the precipitation processes and strengthening mechanisms in a Mg-Al- (Zn) AZ91 alloy [J]. Metallurgical and Materials Transactions A, 2005, 36: 2093-2105.

[18] GHOSH K S, GAO N. Determination of kinetic parameters from calorimetric study of solid state reactions in 7150 Al-Zn-Mg alloy [J]. Transactions of Nonferrous Metals Society of China, 2011, 21: 1199-1209.

[19] BORREGO A,  G. Calorimetric study of 6061-Al-15 vol.% SiCw PM composites extruded at different temperatures [J]. Materials Science and Engineering A, 1998, 245: 10-18.

[20] BARRENA M I,  DE SALAZAR J M, PASCUAL L, SORIA A. Determination of the kinetic parameters in magnesium alloy using TEM and DSC techniques [J]. Journal of Thermal Analysis and Calorimetry, 2013, 113: 713-720.

[21] DONOSO E, DIAZ G, CRIADO J M. Kinetics analysis of precipitation in a quasi-binary Cu-1 at.% CoTi alloy [J]. Journal of Thermal Analysis and Calorimetry, 2008, 91: 491-495.

[22] AVEDESIAN M M, BAKER H [M]. Magnesium and Magnesium Alloys, USA: ASTM International, 1999.

[23] HISA M, BARRY J C, DUNLOP G L. New type of precipitate in Mg-rare-earth alloys [J]. Philosophical Magazine A, 2002, 82: 497-510.

[24] OGUOCHA I N A, YANNACOPOULOS S. Precipitation and dissolution kinetics in Al-Cu-Mg-Fe-Ni alloy 2618 and Al–alumina particle metal matrix composite [J]. Materials Science and Engineering A, 1997, 231: 25-33.

[25] PANSERI C. A resistometric study of preprecipitation in an aluminium-1.4 percent Mg₂Si alloy [J]. Journal of the Institute of Metals, 1966, 94: 99-105.

[26] CERESARA S, DIRUSSO E, FIORINI P, GIARDA A. Effect of Si excess on the ageing behavior of AlMg₂Si 0.8% alloy [J]. Mater Sci Eng, 1969, (5): 220-227.

[27] KOVACS I, LENDVAI J, NAGY E. The mechanism of clustering in supersaturated solid solutions of Al-Mg₂Si alloys [J]. Acta Metallurgica, 1972, 20: 975-983.

[28] ESMAEILI S, VAUMOUSSE D, ZANDBERGEN M W, POOLE W J, CEREZO A, LLOYD D J. A study on the early-stage decomposition in the Al-Mg-Si-Cu alloy AA6111 by electrical resistivity and three-dimensional atom probe [J]. Philosophical Magazine, 2007, 87: 3797-3816.

[29] DONOSO E, G, CRIADO J. Kinetics analysis of precipitation in a quasi-binary Cu-1 at.% CoTi alloy [J]. Journal of Thermal Analysis and Calorimetry, 2008, 91: 491-495.

[30] BURNHAM A, DINH L. A comparison of isoconversional and model-fitting approaches to kinetic parameter estimation and application predictions [J]. Journal of Thermal Analysis and Calorimetry, 2007, 89: 479-490.

[31] VYAZOVKIN S, BURNHAM A K, CRIADO J M, L A, POPESCU C, SBIRRAZZUOLI N. ICTAC kinetics committee recommendations for performing kinetic computations on thermal analysis data [J]. Thermochimica Acta, 2011, 520: 1-19.

[32] FRIEDMAN H L. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic [J]. Journal of Polymer Science (Part C), 1964, 6: 183-195.

电阻法分析NZ30K镁合金的析出动力学

王小娜，韩利战，顾剑锋

上海交通大学 材料科学与工程学院，上海市激光制造与材料改性重点实验室，上海 200240

摘  要：通过测量NZ30K镁合金在连续升温过程中的电阻变化分析其析出动力学。NZ30K镁合金在连续升温过程中有两种析出相出现，即β″ 相和β′相。通过Kissinger法和微分等转变量法得到NZ30K镁合金的析出动力学参数 E_α和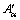，并确定析出量随时间与温度的变化以及NZ30K镁合金的析出序列，进一步得到连续升温转变曲线(CHT)及等温转变曲线(IHT)，以指导NZ30K镁合金的时效工艺。结果表明：等转变量法可用于计算NZ30K镁合金的析出动力学参数。

关键词：NZ30K镁合金；析出动力学；微分等转变量法；连续升温转变；等温转变

(Edited by Chao WANG)

Foundation item: Project (2011ZX04014-052, 2012ZX04012011) supported by CNC Machine Tools and Basic Manufacturing Equipment Technology Comments

Corresponding author: Li-zhan HAN; Tel: +86-21-34203743; E-mail: victory_han@sjtu.edu.cn

DOI: 10.1016/S1003-6326(14)63242-8