J. Cent. South Univ. (2016) 23: 1007-1014
DOI: 10.1007/s11771-016-3149-2
Dynamic recrystallization behavior and kinetics of high strength steel
WU Guang-liang(吴光亮), ZHOU Chao-yang(周超洋), LIU Xin-bin(刘新彬)
School of Minerals Processing and Bioengineering, Central South University, Changsha 410083, China
 Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Central South University Press and Springer-Verlag Berlin Heidelberg 2016
Abstract: The dynamic recrystallization behavior of high strength steel during hot deformation was investigated. The hot compression test was conducted in the temperature range of 950-1150 °C under strain rates of 0.1, 1 and 5 s-1. It is observed that dynamic recrystallization (DRX) is the main flow softening mechanism and the flow stress increases with decreasing temperature and increasing strain rate. The relationship between material constants (Q, n, α and lnA) and strain is identified by the sixth order polynomial fit. The constitutive model is developed to predict the flow stress of the material incorporating the strain softening effect and verified. Moreover, the critical characteristics of DRX are extracted from the stress-strain curves under different deformation conditions by linear regression. The dynamic recrystallization volume fraction decreases with increasing strain rate at a constant temperature or decreasing deformation temperature under a constant strain rate. The kinetics of DRX increases with increasing deformation temperature or strain rate.
Key words: flow stress; dynamic recrystallization kinetics; high strength steel; constitutive model; material constants
1 Introduction
During the high-temperature deformation process, several metallurgical phenomena such as work hardening (WH), dynamic recovery (DRV), and dynamic recrystallization (DRX) occur simultaneously [1-2]. In low stacking fault energy, face-centered cubic alloy and steel, DRX occurs readily during hot working because dynamic recovery is sluggish as climb and cross slip are inhibited so that the driving force for recrystallization is maintained [3]. The DRX softens metals and reduces the hot working loads during hot deformation. Furthermore, it can lead to a significant grain refinement, which will enhance the mechanical properties and thus the formability of the materials [1-3].
In recent research, the microalloying technology coupled with new generation thermo-mechanical control processing (NG-TMCP) is proved efficiently to achieve the proper balance among strength, toughness, ductility, and formability by means of a suitable combination of chemical composition and thermo-mechanical treatment parameters [4-7]. Microalloying elements Ti, Nb, and V are widely used in high strength low alloying (HSLA) steel, and these elements precipitate as carbides and/or carbonitrides at the austenite grain boundary in cooling process. Precipitation hardening together with grain refinement and dislocation strengthening is used to achieve the desired strength and toughness property [5-8].
When adding alloying elements in steel, the dissolved alloying addition in a solid solution raises the temperature of recrystallization of plastically deformed austenite as a result of segregation on the dislocations and grain boundaries, thus causing a decrease in the recovery rate and mobility of grain boundaries [4, 6-8]. Instead, alloying elements precipitating on dislocations in the form of dispersive particles of carbides and/or carbonitrides interstitial phases slow down the course of dynamic recrystallization during plastic deformation [4, 9-10]; Niobium can effectively retard the recovery and recrystallization during hot rolling, whereas vanadium produces greater dispersion hardening retarding the dynamic precipitation of Nb(C, N); titanium provides an improvement in the weld heat affected zone (HAZ) toughness and retardation on DRX kinetics [7, 9, 11-13]. The microstructure control through the DRX process requires a comprehensive knowledge of microstructural evolution as a function of process parameters [12, 14].
The modeling of hot flow stress and the prediction of flow curves are employed in metal-forming processes such as rolling and forging from the mechanical and metallurgical standpoints because any feasible mathematical simulation needs accurate flow description. The characteristic flow behaviors and the associated new grains evolved by DRX have been studied in detail experimentally and theoretically [15-17]. DRX can be initiated at a critical level of stress accumulation during hot deformation. On the flow curve at which the strain hardening rate equals zero, the formation of new grains starts, however DRX actually starts at a critical strain (εc) which is lower than the strain at peak stress [15]. This critical strain is a function of initial microstructure and deformation conditions. So far, many studies have been conducted to study the typical behavior of DRX [18-20].
In high strength steels, the alloy element Ti gets more attentions due to the improvement in metallurgical technology and remarkable decrease in cost compared with V and Nb, and it is widely used in automobile industry. In order to get the appropriate performance and microstructure of high strength steel, the hot flow behavior should be paid more attention. In the majority of previous studies, only the effect of deformation temperature and strain rate was taken into account. However, the influence of strain has not been considered for the development of the constitutive model. The object of this work is to investigate the general nature of the influence of strain, strain rate and temperature on the compressive deformation characteristics of high strength steel by hot compression tests. The model of dynamic recrystallization for hot deformation was used for providing a reliable theoretical basis to make reasonable processing of products. Furthermore, the critical characteristics of DRX were determined using the work hardening rate versus true stress under different hot deformation conditions.
2 Experimental
The chemical composition of the investigated steel is presented in Table 1. Cylindrical hot compression specimens with height of 12 mm and diameter of 8 mm were machined. In order to minimize the frictions between the specimens and die during hot deformation, the flat ends of the specimen were recessed to a depth of 0.1 mm to entrap the lubricant of graphite mixed with machine oil.
Table 1 Main chemical composition of test steel (mass fraction, %)

The hot compression tests were performed on Gleeble-1500 thermo-simulation machine in the temperatures range of 950-1150 °C, at an interval of 50 °C, under constant strain rate of 0.1, 1 and 5 s-1, up to the true strain of 0.9. Each specimen was heated to 1200 °C at a rate of 10 °C/s and held for 3 min, and then cooled to the deformed temperature with the rate of 5 °C/s and held for 30 s. After deformation, the specimens were immediately quenched in tap water. During the whole tests, the high purity argon was used as protective gas. The thermomechanical processing schedule is schematically shown in Fig. 1.
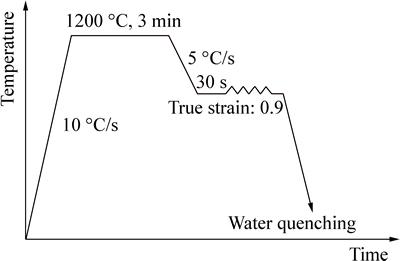
Fig. 1 Schematic diagram of thermomechanical processing schedule
3 Results and discussion
3.1 Analysis of hot flow curves
The effect of deformation temperature and strain rate on the true stress-true strain curves of the investigated steel is shown in Fig. 2.
According to Fig. 2(a), at a constant strain rate, the peak stress and peak strain decrease with an increase in temperature. DRX occurs more easily with the increase of deformation temperature and the decrease of strain rate. For the specimen deformed at 1000 °C under different strain rates, the flow curves show different softening mechanisms in Fig. 2(b). Under the strain rate of 0.1 and 1 s-1, DRX occurs, however, DRV occurs under the strain rate of 5 s-1. Many previous studies [15, 17] also point out that the higher temperatures and lower strain rates can promote the softening process by increasing the mobility of grain boundaries and providing longer time for dislocation annihilation and occurrence of DRX.
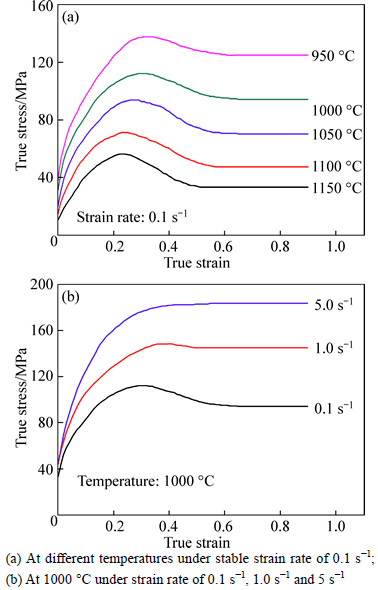
Fig. 2 Flow stress curves of Ti-microalloyed high strength steel:
During the high-temperature deformation process, WH and dynamic softening exist and influence each other at the same time. At the initial stage of straining, the flow stress shows a rapid increase up to a critical value with increasing strain, where WH predominates. As the deformation develops, DRX occurs and the hardening rate decreases. When the hardening rate becomes equal to the softening rate, the peak flow stress is reached. When the flow softening exceeds the hardening, the stress drops gradually. Finally, the flow stress becomes steady when a new balance between softening rate and hardening rate is obtained.
3.2 Establishment and evaluation of constitutive model
Hot working can be considered as a thermally activated process, and it can be described by strain rate equations. The relationship among flow stress, strain rate and temperature can be expressed as hyperbolic sine law (Eq. (1)), the power law (Eq. (2)) and exponential law (Eq. 3) [15]:
 (1)
(1)
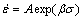 (2)
(2)
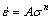 (3)
(3)
where A (s-1), α (MPa-1) and n (stress exponent) are material constants,  is the strain rate (s-1), R is the universal gas constant (8.314 J/(mol·K)), σ is the flow stress (MPa), and Qdef is the activation energy for deformation (J/mol).
is the strain rate (s-1), R is the universal gas constant (8.314 J/(mol·K)), σ is the flow stress (MPa), and Qdef is the activation energy for deformation (J/mol).
The correlation between Zener-Hollomon parameter (Z) and the strain rate can be expressed as follows [17]:
 (4)
(4)
Taking natural logarithm of both sides of Eqs. (2) and (3) at a constant temperature respectively yields
 (5)
(5)
 (6)
(6)
Substituting the values of the flow stress and corresponding strain rate under strain of 0.1 into the Eqs. (5) and (6) gives the relationship between the flow stress and strain rate, as shown in Fig. 3. The value of βand n1 are obtained from the slope of the lines in Fig. 3(a) and Fig. 3(b), respectively. Hence, the value of the constant α at the strain of 0.1 is calculated to be 0.011906 MPa-1.

Fig. 3 Relationship between flow stresses and strain rates at true strain of 0.1 according to exponedtial law (a) and power law (b)
Equation (1) can be changed to another form as Eq. (7), and taking natural logarithm and partial differential from both sides of Eq. (7) and rearranging them, Eq. (8) is derived:
 (7)
(7)
 (8)
(8)
For the parameters, n can be derived from the average slopes of the lines in ln[sinh(ασ)]-ln at all temperature levels with Fig. 4(a), and at the given true strain (ε=0.1), n is 6.89. The parameter b is determined from the slope of ln[sinh(ασ)]-1/T at different strain rates (Fig. 4(b)). The value of Qdef at the true strain of 0.1 is obtained as 535.40 kJ/mol. The value of lnA can be derived from the slope of line in lnZ-sinh(ασ) curves, in Fig. 5. The value of lnA at the true strain of 0.1 is calculated to be 44.382.
at all temperature levels with Fig. 4(a), and at the given true strain (ε=0.1), n is 6.89. The parameter b is determined from the slope of ln[sinh(ασ)]-1/T at different strain rates (Fig. 4(b)). The value of Qdef at the true strain of 0.1 is obtained as 535.40 kJ/mol. The value of lnA can be derived from the slope of line in lnZ-sinh(ασ) curves, in Fig. 5. The value of lnA at the true strain of 0.1 is calculated to be 44.382.
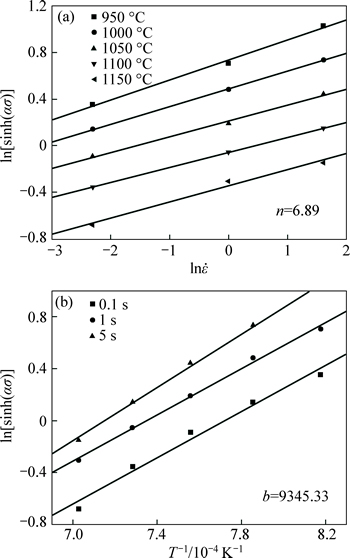
Fig. 4 Relationships between deformation temperature (a), strain rate (b) and stress of high strength steel
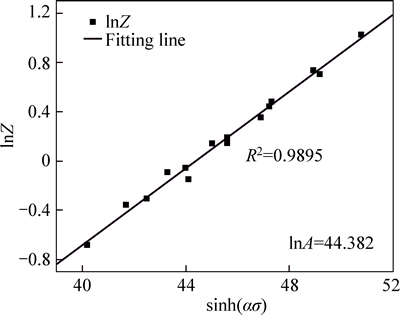
Fig. 5 Relationships between sinh(ασ) and lnZ
In order to describe the relationship between true strain and the material constants (α, n, Q and lnA) under different strain rates and deformed temperatures, the values are chosen in the true strain range of 0.1-0.9 with an interval of 0.05, as shown in Fig. 6.
Figure 6 exhibits that the value of each material parameter drops gradually to a relatively steady state as true strain increases. By mathematic calculation, the appropriate correlation between true strain and material parameters can be given by the sixth order polynomial functions (Eqs. (9)-(12)). The coefficients of the sixth order polynomial functions are given in Table 2.
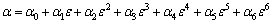 (9)
(9)
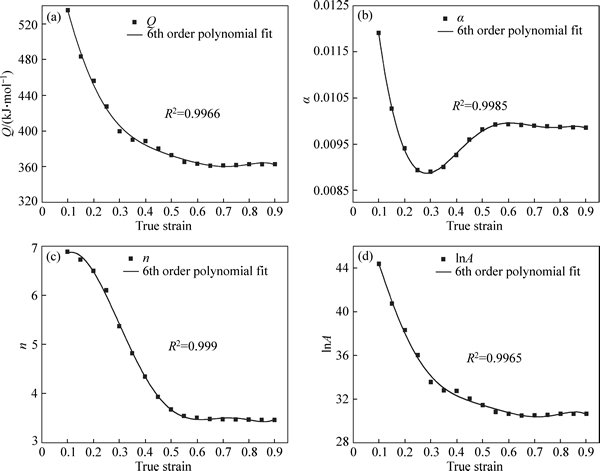
Fig. 6 Variations of material constants Q (a), α (b), n (c) and lnA (d) as a function of true strain using a sixth order polynomial fit for investigated microalloyed steel
 (10)
(10)
 (11)
(11)
 (12)
(12)
Table 2 Coefficients of sixth order polynomial function for α, Q, n and lnA

The flow stress in the temperature range of 950-1150 °C, under strain rates of 0.1, 1 and 5 s-1 can be calculated at a particular strain, using the following equation [16-17]:
 (13)
(13)
The values calculated by Eq. (13) are compared with the experimental data in Figs. 7(a), (b) and (c). The precision of the constitutive model is verified in Fig. 7(d).
From Figs. 7(a), (b) and (c), it can be seen that the constitutive model can efficiently predict the flow stress of the investigated material over the entire range of deformation conditions. The precision in Fig. 7(d) shows that most data points lie fairly close to the best regression line and the square correlation coefficient for the constitutive model is 0.9962. In conclusion, the constitutive model can effectively predict the high temperature flow behavior of the investigated steel.
3.3 Behavior of DRX
Generally speaking, DRX can be initiated at a critical level of stress accumulation during hot deformation. However, DRX actually starts at a critical strain (εc) which is lower than the strain at peak stress [15]. Only when the strain exceeds εc, DRX occurs in hot deformation process. So, it is important to accurately confirm εc in the research of hot deformation parameters.
On the flow curve, the point at which the strain hardening rate equals zero represents the peak stress (σp) and the inflection point indicates the critical stress (σc) for the initiation of DRX. The critical strains can be determined from the inflection points of the lnθ-εplots and the critical stresses can be subsequently obtained either from the θ-σ plots or from the initial flow curves [21]:
lnθ=A1ε3+A2ε2+A3ε+A4 (14)
where A1, A2, A3 and A4 are constant parameters for each deformation condition. The second derivative of Eq. (14) with respect to ε can be expressed as
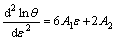 (15)
(15)
At critical stress for initiation of DRX, the second derivative becomes zero. Therefore,
εc=-A2/(3A1) (16)
The lnθ-ε curves and its corresponding third order polynomial are shown in Fig. 8. As it can be seen, the 3rd curve has a good fit. Therefore, this method is used to determine the value of critical stress at different deformation conditions. Using the flow curves, the values of peak and critical stresses and strains are determined. The results are given in Table 3.
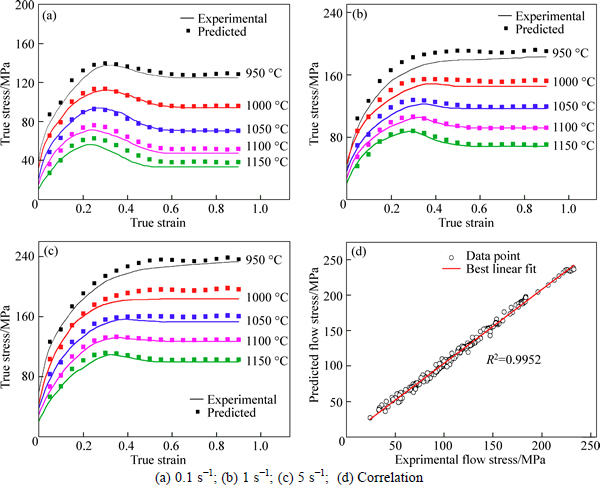
Fig. 7 Comparison between experimental and predicted flow stresses at different constant strain rates:
According to Table 3, the critical and peak strains increase with an increase of the strain rate at a constant temperature. However, these parameters increase as the deformation temperature decreases at a constant strain rate. The average ratio of εc/εp is 0.50.
During the hot deformation process, the peak strain and critical strain are determined by Z and ε. At a constant value of Z parameter, the microstructure of material undergoes the process of WH, DRV, partial recrystallization and full recrystallization. According to the calculated values of calculated εc, εp and Z parameter, the relationship among εc, εp and Z parameter are shown in Fig. 9.
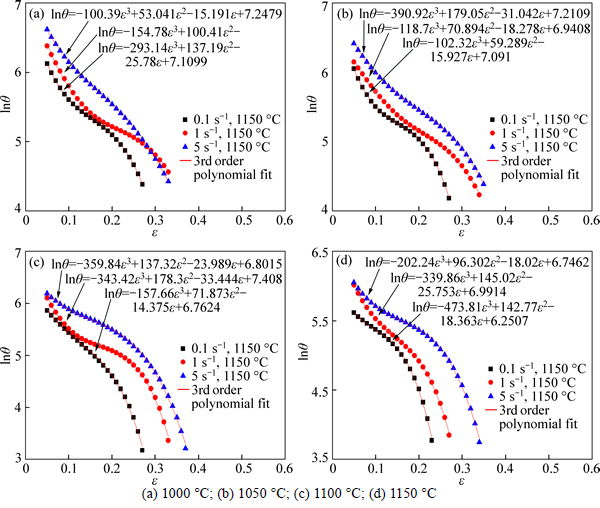
Fig. 8 lnθ-ε curves under hot deformation conditions at different strain rates and temperature:
Table 3 Critical and peak strains at different deformation conditions

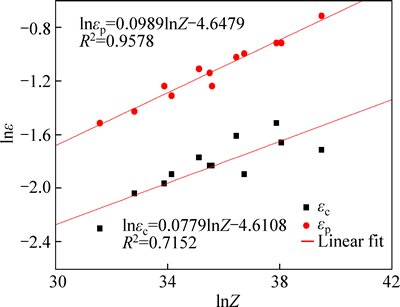
Fig. 9 Relation among εc, εp and Z parameter
Figure 9 exhibits the linear regression results of critical and peak strain on the Zener-Hollomon parameter. It can be seen that the critical characteristics of DRX increase with increasing Z parameter. The relationship between these parameters and deformation conditions is expressed by a power law equation (AZn, where A is a constant and n is a power law exponent). According to the linear regression results, the following equations hold for the investigated steel:
εp=9.58×10-3Z 0.0989 (17)
εc=9.94×10-3Z 0.0779 (18)
According to Eq. (4), Eq. (17) and Eq. (18), the model of dynamic recrystallization of high strength steel can be acquired by using the software MATLAB, as shown in Fig. 10.
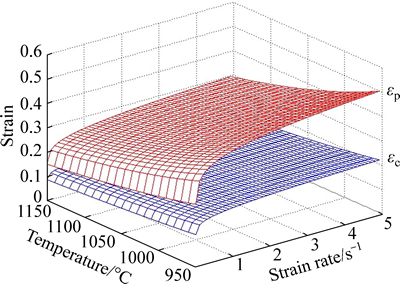
Fig. 10 Model of dynamic recrystallization of high strength steel
In Fig. 10, the space is divided to three parts by the red surface and blue surface. The red surface (εp) represents the critical condition of full DRX and the blue surface (εc) means critical condition of DRX. When the deformation parameters are above εp, between εp and εc, and below εc, the related recrystallization is full DRX, partial DRX and no DRX, respectively.
The volume fraction of DRX (Xd) can be expressed as follows [22]:
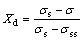 (19)
(19)
where σss is steady stress, σ is the stress on DRX curve, and σs is the stress on DRV curve.
The DRX time (t) from peak strain (εp) to strain of ε may be determined by [2]
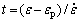 (20)
(20)
The relationship among Xd, ε, T and t are shown in Fig. 11.
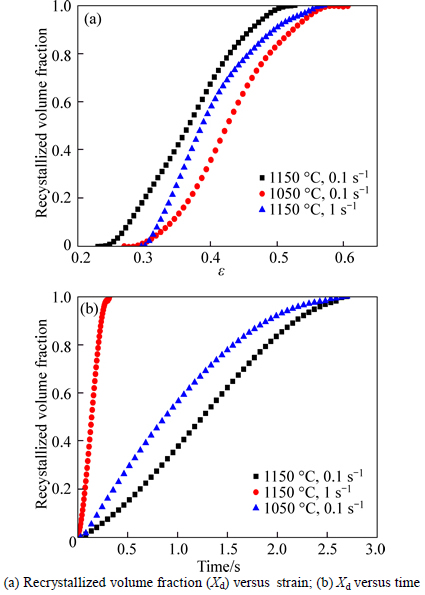
Fig. 11 Effect of deformation temperature and strain rate on kinetics of DRX:
Figure 11(a) shows that the recrystallization curve moves to right by increasing strain rate at the constant temperature of 1150 °C or decreasing deformation temperature under constant strain rate of 0.1 s-1.Figure 11(b) illustrates that the DRX volume fraction (Xd) increases with the increasing of strain rate and decreasing of temperature.
4 Conclusions
1) The material parameters in the constitutive equation (Q, n, A and α) are identified by a sixth order polynomial fit. The constitutive model containing strain achieves a good match with the experimentally recorded flow stress of the investigated steel
2) The εp and εc can be expressed as εp=9.58× 10-3Z0.0989 and εc=9.94×10-3Z 0.0779, respectively.
3) The DRX volume fraction decreases with increasing strain rate at a constant temperature or decreasing deformation temperature under a constant strain rate. However, the kinetics of DRX increases with increasing deformation temperature or strain rate.
References
[1] WU Lai-zhi, LI Xue-song, CHEN Jun, ZHANG Hong-bing, CUI Zhen-shan. Dynamic recrystallization behavior and microstructural evolution in SPHC steel [J]. Journal of Shanghai Jiaotong University (Science), 2010, 15(3): 301-306.
[2] MIRZADEH H, NAJAFIZADEH A. Prediction of the critical conditions for initiation of dynamic recrystallization [J]. Materials and Design, 2010, 31(3): 1174-1179.
[3] MANDAL S, BHADURI A K, SARMA V S. A study on microstructural evolution and dynamic recrystallization during isothermal deformation of a Ti-modified austenitic stainless steel [J]. Metallurgical and Materials Transactions A, 2011, 42(4): 1062-1072.
[4] BANDYOPADHYAY P S, KUNDU S, GHOSH S K, CHATTERJEE S. Structure and properties of a low-carbon microalloyed ultra-high- strength steel [J]. Metallurgical and Materials Transactions A, 2011, 42(4): 1051-1061.
[5] SHUKLA R, DAS S K, RAVIKUMAR B, GHOSH S K, KUNDU S, CHATTERJEE S. An ultra-low carbon, thermomechanically controlled processed microalloyed steel: Microstructure and mechanical properties [J]. Metallurgical and Materials Transactions A, 2012, 43(12): 4835-4845.
[6] OPIELA M. Effect of thermomechanical processing on the microstructure and mechanical properties of Nb-Ti-V microalloyed steel [J]. Journal of Materials Engineering and Performance, 2014, 23(9): 3379-3388.
[7] CHEN Bing-hua, YU Hao. Hot ductility behavior of V-N and V-Nb microalloyed steels [J]. International Journal of Minerals, Metallurgy and Materials, 2012, 19(6): 525-529.
[8] RAJPUT S K, CHAUDHARI G P, NATH S K. Physical simulation of hot deformation of low-carbon Ti-Nb microalloyed steel and microstructural studies [J]. Journal of Materials Engineering and Performance, 2014, 23(8): 2930-2942.
[9] MA Li-qiang, LIU Zhen-yu, JIAO Si-hai, YUAN Xiang-qian, WU Di. Dynamic recrystallization behaviour of Nb-Ti microalloyed steels [J]. Journal of Wuhan University of Technology-Materials Science Edition, 2008, 23(4): 551-557.
[10] SAIKALY W, CHARRIN L,  A, BANO X, ISSARTEL C. The effects of thermomechanical processing on the precipitation in an industrial dual-phase steel microalloyed with titanium [J]. Metallurgical and Materials Transactions A, 2001, 32(8): 1939-1947.
A, BANO X, ISSARTEL C. The effects of thermomechanical processing on the precipitation in an industrial dual-phase steel microalloyed with titanium [J]. Metallurgical and Materials Transactions A, 2001, 32(8): 1939-1947.
[11] NIU Tao, KANG Yong-lin, GU Hong-wei, YIN Yu-qun, QIAO Ming-liang, JIANG Jin-xing. Effect of Nb on the dynamic recrystallization behavior of high-grade pipeline steels [J]. International Journal of Minerals, Metallurgy, and Materials, 2010, 17(6): 742-747.
[12]  B, RODRIGUEZ-IBABE J M. Effect of deformation temperature on microstructure and mechanical behaviour of warm working vanadium microalloyed steels [J]. Journal of Materials Science, 2011, 46(11): 3725-3737.
B, RODRIGUEZ-IBABE J M. Effect of deformation temperature on microstructure and mechanical behaviour of warm working vanadium microalloyed steels [J]. Journal of Materials Science, 2011, 46(11): 3725-3737.
[13] ZENG Y, WANG W. Computer simulation of carbonitride precipitation during deformation in Nb-Ti microalloyed steels [J]. Journal of Materials Science, 2008, 43(3): 874-882.
[14] ARAB N B M, AYAZ M, KHAKI D M. Statistical modeling of strain-hardening exponent and grain size of Nb-microalloyed steels using a two-level factorial design of experiment [J]. Journal of Materials Engineering and Performance, 2013, 22(11): 3337-3347.
[15] FERDOWSI M R G, NAKHAIE D, BENHANGI P H, EBRAHIMI G R. Modeling the high temperature flow behavior and dynamic recrystallization kinetics of a medium carbon microalloyed steel [J]. Journal of Materials Engineering and Performance, 2014, 23(3): 1077-1087.
[16] CABRERA J M, OMAR A A , PRADO J M, JONAS J J. Modeling the flow behavior of a medium carbon microalloyed steel under hot working conditions [J]. Metallurgical and Materials Transactions A, 1997, 28(11): 2233-2244.
[17] MIRZADEH H, CABRERA J M, NAJAFIZADEH A. Modeling and prediction of hot deformation flow curves [J]. Metallurgical and Materials Transactions A, 2012, 43(1): 108-123.
[18] HUANG Shi-quan, YI You-ping, LI Peng-chuan, HE Hai-lin. Simulation of dynamic recrystallization in 23Co13Ni11Cr3Mo steel using a modified cellular automaton [J]. Journal of Central South University, 2014, 21(2): 454-459.
[19] YANG Zhi-qiang, LIU Yong, TIAN Bao-hong, ZHANG Yi. Model of critical strain for dynamic recrystallization in 10%TiC/Cu-Al2O3 composite [J]. Journal of Central South University, 2014, 21(11): 4059-4065.
[20] GU Sen-dong, ZHANG Li-wen, RUAN Jin-hua, ZHOU Ping-zhen, ZHEN Yu. Constitutive modeling of dynamic recrystallization behavior and processing map of 38MnVS6 non-quenched steel [J]. Journal of Materials Engineering and Performance, 2014, 23(3): 1062-1068.
[21] POLIAK E I, JONAS J J. Initiation of dynamic recrystallization in constant strain rate hot deformation [J]. ISIJ International, 2003, 43(5): 684-691.
[22] WAHABI M E, CABRERA J M, PRADO J M. Hot working of two AISI 304 steels: A comparative study [J]. Materials Science and Engineering A, 2003, 343(1/2): 116-125.
(Edited by YANG Bing)
Foundation item: Project(51322405) supported by the National Natural Science Foundation of China; Project(CX2013B085) supported by Hunan Provincial Innovation Foundation for Postgraduate, China
Received date: 2015-03-18; Accepted date: 2015-07-22
Corresponding author: WU Guang-liang, Professor, PhD; Tel: +86-15802567389; E-mail: glwu_899@sina.com