氧化铝种分过程粒度分布的动态模型
张家元1,李永清2,付明辉1,刘 斌1
(1. 中南大学 能源科学与工程学院,湖南 长沙,410083;
2. 湖南工业大学 冶金工程学院,湖南 株州,412007)
摘 要:将实验室实验、工业试验与数值仿真(计算)方法相结合,以种分过程中的动力学规律和粒数衡算为基础,以 MATLAB/Simulink软件为主要开发工具,根据种分过程的粒度变化特性,以MSMPR结晶器为对象,建立种分槽晶体成核、生长和附聚相结合的粒度衡算模型。根据不同温度下的实验数据,利用矩量法对种分过程的重要参数——附聚核β和成核速率RN进行求解。计算结果表明:附聚核在70 ℃左右达到最大值,成核速率则一直随着温度的升高而降低;用MATLAB/Simulink软件求解粒度模型,对不同工艺条件下种分过程的粒度分布进行预测,将预测结果与工业试验数据进行比较,相对误差低于10%。
关键词:氧化铝;种分过程;粒度;模型
中图分类号:TF803.22 文献标识码:A 文章编号:1672-7207(2009)04-0879-05
Particle distribution dynamic model of gibbsite precipitation process during alumina production
ZHANG Jia-yuan1, LI Yong-qing2, FU Ming-hui1, LIU Bin1
(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;
2. School of Metallurgical Engineering, Hunan University of Technology, Zhuzhou 412007, China)
Abstract: The laboratory experiment, industrial test and numerical simulation of the precipitation were synchronously applied. Based on the dynamics law and population balance, with the full characteristics of the particle size variation of the MSMPR gibbsite precipitation process, the combined dynamic model of crystal’s nucleation, growth and agglomeration was developed with MATLAB/Simulink to confirm the value of the important parameters β and RN in different experimental conditions. The results show that β is maximal at about 70 ℃and RN decreases with the increase of temperature. And the particle size distribution is predicted with the dynamic model. The relative error between the model’s prediction and the experimental test data is less than 10%.
Key words: alumina; gibbsite precipitation process; particle; model
20世纪 70年代,随着干法氧化氢净化技术的问世和大型点式下料预焙阳极电解槽的开发应用,对氧化铝的质量指标特别是物理性能提出了新的要求,生产粗粒度和高强度的砂状氧化铝已成为发展趋势[1]。拜耳法种分生产砂状氧化铝新工艺在氧化铝生产中应用更加广泛[2-3]。由于实际种分过程中存在成核、生长、附聚和破损等过程,比理想种分过程要复杂得多,所以,对实际种分过程的粒度分布进行预测是比较困难的,需建立一个同时包括成核、生长、附聚及破损过程的综合作用对种分产品粒度分布影响的仿真模 型[3],该模型以粒数衡算式为基础[4]。
国内外研究者针对其铝土矿特点,对低浓度、低摩尔比的铝酸钠溶液种分过程建立了一些静态种分模型,而对动态种分模型的研究尚未见公开报道[5]。大部分对实际工业体系的分解过程的研究只是运用了一部分动力学基础研究的定性结果[4, 6]。由于种分过程的复杂性,适合中国铝土矿特点的种分过程的准确数学模型和种分参数的求解都还有待于进一步研究。由于粒数衡算式的边界条件和初始条件是随着结晶体系、操作方式和过程条件的不同而发生改变的,影响因素复杂,直接求解比较困难[5]。分类法计算简单、运算速度快以及运算精度能够满足工程设计的需求而被广泛应用于粒数衡算模型的求解[5-6]。在此,本文作者利用分类法建立MSMPR结晶器的粒度模型并用Matlab/ Simulink对模型进行求解,同时,利用工业试验数据对模型进行验证。
1 用分类法建立成核、生长和附聚综合过程的粒度衡算数学模型
将整个粒度区间分成N(2≤N<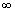 )个,对应的节点粒度从小到大分别为L0, L1, …, LN。其中:L0为晶体的最小粒度,LN为晶体的最大粒度。第i(2≤i≤N)个区间的长度?L=Li-Li-1。在t时刻,单位浆液体积内第i个粒度区间的粒子数为[5]:
)个,对应的节点粒度从小到大分别为L0, L1, …, LN。其中:L0为晶体的最小粒度,LN为晶体的最大粒度。第i(2≤i≤N)个区间的长度?L=Li-Li-1。在t时刻,单位浆液体积内第i个粒度区间的粒子数为[5]:
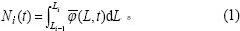
在粒度Li-1~Li的范围内对式(1)进行积分,有[5, 7]:

对于MSMPR结晶器,在结晶过程中,晶体很少有机会被破碎为若干粒度较小的碎块[8],所以,粒数衡算式(2)中破碎粒子数可取为0,即RB, i=0。这样,可以得到考虑成核、生长和附聚情况下的粒数衡算 方程:

2 Simulink模型的建立
在上述模型的基础上,可以建立Simulink模型来求解种分槽的粒度分布。模型需满足以下3个条件[9]:
a. 分解槽是MSMPR结晶器,进口浆液的体积流量和出口浆液的体积流量相等,即Q=Qe,从而有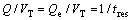 。
。
b. 粒子附聚与颗粒粒度无关,不同粒度区间的附聚核相等。
c. 晶体的生长满足?L定律,即生长速率G与粒度无关,而且符合生长规律,即Al(OH)3的结晶过程是受表面反应控制并且与过饱和度成平方关系,与苛性碱浓度的关系为指数关系[10],即

用分类法将晶体的粒度分为20个离散的粒度区间,即N=20。在Matlab的工作空间中输入初始晶种的粒度分布和工艺条件(分解温度、苛碱浓度、固含、氧化铝浓度、停留时间等),通过模型计算就可以得到在分解过程中各个粒度区间粒子数随时间的变化情况。综合各个离散的粒度区间粒子数的变化就可以得到整个粒度范围的晶体粒度分布变化。
3 模型的求解
由粒数衡算方程可知,上述Simulink模型中含有种分过程中的重要参数:附聚核β和成核速率RN。有研究者[11-12]通过实验数据回归得到了一些经验或者半经验关系式,但都是从各自的实验条件出发,适用范围有限[11]。本文采用矩量法(Method of moments)处理实验数据,对模型中的参数进行求解。
定义体积的j阶矩量变换为:
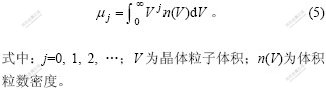
对粒数平衡方程进行矩量变换,可以得到成核速率RN和附聚核β的计算式分别为[13]:
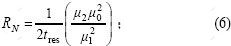
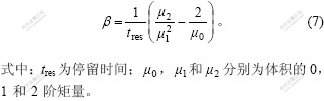 这样,就可以通过激光粒度仪测出实验室种分实验得到的Al(OH)3晶体的粒度分布,由式(8)计算出0~2阶矩量,代入式(6)和(7)计算出成核速率和附聚核。
这样,就可以通过激光粒度仪测出实验室种分实验得到的Al(OH)3晶体的粒度分布,由式(8)计算出0~2阶矩量,代入式(6)和(7)计算出成核速率和附聚核。
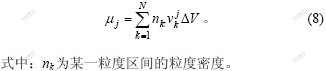
在实验室进行不同分解温度条件下的种分实验,实验条件如表1所示。由激光粒度仪测出晶种和分解反应后晶体的粒度分布[14-15]。由粒度分布数据可计算得到不同温度下的种分过程参数,如表2所示。
表1 种分实验条件
Table 1 Experimental conditions of gibbsite precipitation process
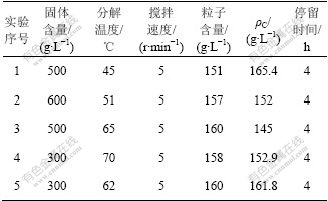
表2 不同温度下的种分过程参数
Table 2 Parameters of gibbsite precipitation process at different temperatures
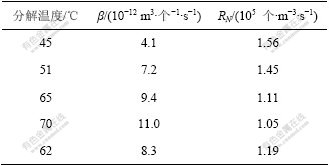
从表2可知,分解过程存在一个最佳的附聚温度,附聚核在70 ℃左右时达到最大值。当温度低于70 ℃时,附聚核随着温度的升高而增加;当温度超过70 ℃后,附聚核随着温度的升高而减少;而成核速率随着温度的升高而降低。
4 粒度模型预测结果与工业实际试验结果的比较
实验中分解槽的温度、进出料流量、固含和浆液苛碱浓度都可看作基本不变。温度由各槽中测温热电偶测得;在各槽进、出料口取分解浆液,固液分离,测得固含;液体样由滴定分析测得苛碱浓度及苛性比,固体样由激光粒度仪测得粒度分析数据。在Matlab的工作空间中输入分解反应初始条件和相应的参数后运行粒度模型,就能求得分解槽在相应工艺条件下的粒度分布。在70.29 ℃和69.52 ℃时的模型计算结果与实测粒度分布的比较如图1和图2所示。
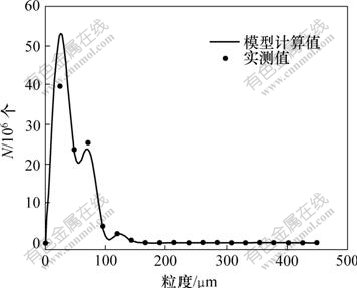
图1 70.29 ℃时的模型计算值与实测值比较
Fig.1 Comparison of value of model and
experimental at 70.29 ℃
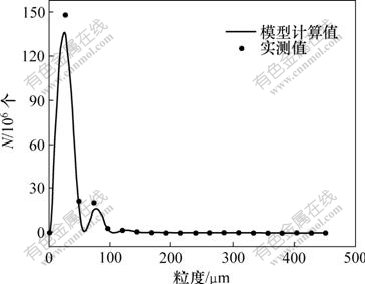
图2 69.52 ℃时的模型粒度计算值与实测值比较
Fig.2 Comparison of value of model and
experimental at 69.52 ℃
由图1和图2可见,实测值与预测值在粒度较小的范围内差别显著,这是由于该条件下主要发生成核过程,使细小粒子比例增多。而在粒度较大的范围内,实测值与模型预测值基本一致。另外,Sweeger[6]对种分成核过程研究认为,在过饱和度较高、温度较低时,成核过程相对容易发生,图1和图2所示结果论证了这一点。
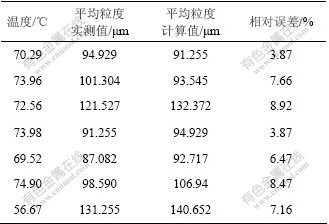
为了使模型计算值与实测值比较更加精确,用平均粒度作为衡量模型预测结果好坏的标准,平均粒度的定义如下:

模型计算的平均粒度与实测的平均粒度的比较如表3所示。从表3可以看出,粒度模型预测的结果与实测的结果的相对误差在10%以内,基本上满足生产砂状氧化铝的粒度要求。
表3 不同温度下的平均粒度对比
Table 3 Comparison of average particle at different temperatures
5 结 论
a. 建立单种分槽晶体成核、生长和附聚相结合的粒度模型,并利用矩量法对种分过程的参数进行求解,计算出不同工艺条件下对应的种分参数范围。用粒度模型对不同工艺条件下的种分过程的粒度分布进行预测,将预测结果与试验厂工业试验数据进行比较,相对误差在10%以内,基本上满足生产要求。
b. 通过所建立的粒度模型来预测在生产现场设定的工艺条件下氢氧化铝的粒度分布,从而判断该工艺是否能达到生产砂状氧化铝的粒度要求。
参考文献:
[1] 毕诗文, 于海燕. 氧化铝生产工艺[M]. 北京:化学工业出版社, 2006.
BI Shi-wen, YU Hai-yan. Alumina production technology[M]. Beijing: Chemistry Industrial Press, 2006.
[2] 吴玉胜, 毕诗文, 杨毅宏. 种分生产砂状氧化铝的研究进展[J]. 轻金属, 2005(12): 13-17.
WU Yu-sheng, BI Shi-wen, YANG Yi-hong. Development of producings and alumina in seed precipitation[J]. Light Metals, 2005(12): 13-17.
[3] 王熙慧, 于海燕, 陈 涛, 等. 高浓度铝酸钠溶液生产砂状氧化铝的新工艺[J]. 轻金属, 2007(8): 35-37.
WANG Xi-hui, YU Hai-yan, CHEN Tao, et al. New technics of producing sandy alumina with high concentration sodium zluminate solution[J]. Light Metals, 2007(8): 35-37.
[4] Tatollah F, Masoud B B. Mechanism and estimation of Al(OH)3 crystal growth[J]. Journal of Crystal Growth, 2002, 234: 721-730.
[5] 程 立, 陈肖虎. 制取砂状氧化铝时分解过程的数学模型[J]. 贵州工业大学学报: 自然科学版, 2002(5): 22-24.
CHENG Li, CHEN Xiao-hu. The model of the precipitation of sodium aluminate solution[J]. Journal of Guizhou Technical University, 2002(5): 22-24.
[6] Sweeger C. Morphology, evolution and other characteristics of gibbsite crystals grown from pure and impure aqueous sodium aluminate solutions[J]. Journal of Crystal Growth, 2001, 233: 567-582.
[7] 白万全. 拜耳法种分附聚动力学初步研究[J]. 轻金属, 2004(10): 11-14.
BAI Wan-quan. Preliminary study of agglomeration dynamics on crystalline particles in Bayer process[J]. Light Metals, 2004(10): 11-14.
[8] 张江峰, 李旺兴, 尹周澜. 铝酸钠溶液晶种分解附聚过程主要影响因素研究[J]. 轻金属, 2004(9): 17-19.
ZHANG Jiang-feng, LI Wang-xing, YIN Zhou-lan. Study of agglo meration during the precipitation of sodium aluminate solution[J]. Light Metals, 2004(9): 17-19.
[9] 吴玉胜, 毕诗文, 李文成. 分解过程氢氧化铝产品粒度变化机理及规律[J]. 中国有色金属学报, 2005, 15(12): 2061-2065.
WU Yu-sheng, BI Shi-wen, LI Wen-cheng. Mechanism and rule of Al(OH)3 particles variation in seed precipitation[J]. The Chinese Journal of Nonferrous Metals, 2005, 15(12): 2061-2065.
[10] 谭 军, 陈启元, 尹周澜, 等. 分形在砂状氧化铝强度研究中的应用[J]. 中南大学学报: 自然科学版, 2005, 36(5): 834-836.
TAN Jun, CHEN Qi-yuan, YIN Zhou-lan, et al. Application of fractal theory to studying strength of sandy alumina[J]. Journal of Central South University: Science and Technology, 2005, 36(5): 834-836.
[11] Ginter D M, Loyalka S K. Apparent size-dependent growth in aggregation crystallizers[J]. Chemical Engineering Science, 1996, 51(14): 3685-3695.
[12] Caliane B B C. Considerations on the crystallization modeling: Population balance solution[J]. Computers and Chemical Engineering, 2006, 6(5): 1-12.
[13] Gomez M J. Crystal size distribution of hydroxyapatite precipitated in a MSMPR reactor[J]. Cryst Res Technol, 2001(36): 1065-1074.
[14] 刘吉波, 刘 斌, 张家元, 等. 氧化铝种分过程理论生长模型[J]. 轻金属, 2006(9): 26-28.
LIU Ji-bo, LIU Bin, ZHANG Jia-yuan, et al. Theoretical growth model of gibbsite precipitation process during alumina production[J]. Light Metal, 2006(9): 26-28.
[15] 刘 斌, 刘吉波, 张家元, 等. 氧化铝种分过程的粒度分析[J]. 有色金属, 2006(5): 25-27.
LIU Bin, LIU Ji-bo, ZHANG Jia-yuan, et al. Analysis of particle size distribution during seed precipitation process of alumina[J]. Nonferrous Metal, 2006(5): 25-27.
收稿日期:2008-10-15;修回日期:2008-12-02
基金项目:中国博士后基金资助项目(291054)
通信作者:张家元(1968-),男,湖北浠水人,博士,副教授,从事热能与动力工程研究;电话:0731-88876111; E-mail: zjyzhq@mail.csu.edu.cn