
Evaluation of forming limit in viscous pressure forming of
automotive aluminum alloy 6k21-T4 sheet
WANG Zhong-jin(王忠金)1, LI Yi(李 毅)1, LIU Jian-guang(刘建光)1, ZHANG Yi-he(张义和)2
1. School of Materials Science and Engineering, Harbin Institute of Technology, Harbin 150001, China
2. Research and Development Center, China FAW Group Corporation, Changchun 130011, China
Received 15 July 2007; accepted 10 September 2007
Abstract: A ductile fracture criterion is introduced into numerical simulation to predict viscous pressure forming limit of the automotive body aluminum alloy 6k21-T4. The material constant in the ductile fracture criterion is determined by the combination of the viscous pressure bulging (VPB) test with numerical simulation. VPB tests of the aluminum alloy sheet are carried out by using various elliptical dies with different ratios of major axis to minor axis(β), and the bugling processes are simulated by the aid of the finite element method software LS-DYNA3D. On the basis of the stress and strain calculated from numerical simulations, the forming limits of bulging specimens obtained are predicted by the ductile fracture criterion, and compared with experimental results. The fracture initiation site and the minimal thickness predicted by the ductile fracture criterion are in good agreement with the experimental results.
Key words: aluminum alloy sheet; viscous pressure forming limit; ductile fracture criteria; finite element analysis
1 Introduction
Mass reduction is one of the key problems in the automotive industries. With the lower density and good mechanical properties, aluminum alloy becomes the ideal material to replace heavier materials in the car. However, aluminum alloy has poorer room-temperature formability than steel. This can result in restrictions in part geometry, then limiting automotive design[1]. Therefore, the new technology that can improve the formability of aluminum alloy sheet is required.
Viscous pressure forming(VPF) is a new sheet flexible forming technology. The previous investigations show that VPF can improve the sheet formability[2-7]. VPF uses a semi-solid, flowable, highly viscous and strain rate sensitive macromolecule polymer (called viscous medium) as the forming flexible-punch. Because of high viscosity and strain rate sensitivity, the viscous medium can produce a non-uniform pressure field adaptively to the deformation of the sheet metal and improve the stress distribution of the sheet to reduce spring-back of formed panels. So VPF is in favor of forming the aluminum alloy sheet with lower ductility and higher spring-back.
The forming limit of the sheet metal is predicted by the onset of localized necking in the conventional approaches[8-11]. In case of aluminum alloy with lower ductility, fracture often occurs before necking instability. So, the conventional approaches don’t fit for prediction of the forming limit of aluminum alloy sheet. Because ductile fracture criteria have been widely used in the bulk forming process, they are recently introduced into the forming limit prediction in sheet metal forming processes [12-16]. In the ductile fracture criterion, the occurrence of ductile fracture is usually estimated by the stress and strain during forming. The distributions and the histories of stress and strain are calculated by finite element analysis of sheet metal forming. The forming limit can be predicted by the combination of finite element analysis with the ductile fracture criterion. TAKUDA et al[17] successfully predicted the forming limits in deep drawing of the Fe/Al laminated composite sheets by using Oyane criterion (one of ductile fracture criteria) [18]. Axisymmetric bore-expanding was simulated by the rigid/plastic finite element method. The fracture initiation site and the critical stroke were predicted by means of the ductile fracture criterion[19]. TAKUDA etal[13] also carried out calculations for various strain paths from balanced biaxial stretching to uniaxial tension of aluminum alloy sheets and predicted the forming limit diagrams. JAIN et al[20] predicted the forming limit of AA6111-T4 sheet by means of various ductile fracture criterion and assessed the applicability of the different fracture criteria.
In this study, VPB tests of the automotive aluminum alloy 6k21-T4 sheet are carried out with various strain paths and the processes are simulated by the finite element code LS-DYNA3D. A ductile fracture criterion is applied to predict the forming limits of VPB specimens.
2 Ductile fracture criterion
Since the history of deformation affects the forming limit of sheet metal, it is necessary for a criterion to allow for the history of stress and strain affecting the occurrence of the ductile fracture. In this study, Cockroft-Latham criterion[21] is used to predict the forming limit of the automotive aluminum alloy 6k21-T4 sheet. The criterion is expressed as
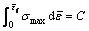 (1)
(1)
where σmax is the maximal principle stress,  is the equivalent strain at which the fracture occurs,
is the equivalent strain at which the fracture occurs, 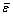 is the equivalent strain during deformation, and C is a material constant.
is the equivalent strain during deformation, and C is a material constant.
To predict the forming limit by means of Eqn.(1), the material constant C is determined by the combination of viscous pressure bulging(VPB) tests with finite element analysis. The bugling process is simulated by the finite element code. When the minimum thickness of the simulative specimen reaches that of the experimental specimen, the fracture to occur is determined. The material constant C is determined by substituting stress and strain values obtained from the finite element analysis into the ductile fracture criterion.
Here, we define the integral Ci, modifying Cockroft and Latham criterion (Eqn.(1)) as
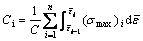 (2)
(2)
when Ci equals 1, the condition of fracture is satisfied.
3 Experiment and finite element modeling
3.1 Experiment materials
The aluminum alloy sheet used in experiments is 6k21-T4 with a thickness of 1.2 mm. Its chemical composition and material properties are listed in Tables 1 and 2, respectively. The viscous medium is methyl vinyl silicone rubber. The flow stress vs. strain rate curve of the viscous medium is shown in Fig.1.
Table 1 Chemical composition of 6k21-T4 aluminum alloy (mass fraction, %)
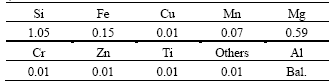
Table 2 Material properties of 6k21-T4 aluminum alloy

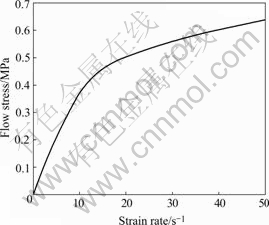
Fig.1 Flow stress vs strain rate curve of viscous medium
3.2 Viscous pressure bugling test
The principle sketch of the viscous pressure bugling test is shown in Fig.2. The forming operation is carried out on the 4 000 kN hydraulic press. The sheet is clamped through a blank holder bead, and the blank holder force is provided by the hydraulic press. A piston pushes the viscous medium upwards and the sheet is bugled. The blank is square with 180 mm×180 mm in size and circle grids with the diameter of 3 mm are printed on the blank surface to measure the strain distribution of specimens.
In order to obtain the limit strains under various strain paths, elliptical dies with four ratios of major axis to minor axis(β) are used, as shown in Fig.2. Dimensions of various elliptical dies are listed in Table 3.
Table 3 Dimensions of various elliptical dies

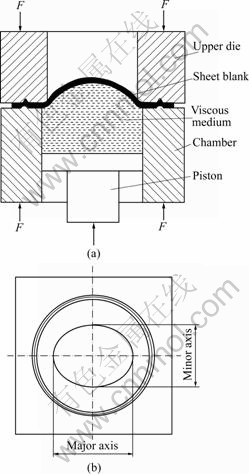
Fig.2 Sketch of viscous pressure bulging test and elliptical die used in test: (a) Sketch of bulging test; (b) Elliptical die
3.3 Finite element modeling
One quarter of the blank is modeled due to symmetric boundary condition, as seen in Fig.3. VPB tests are simulated using commercially available finite element code LS-DYNA3D. In calculations, Barlat’s yield function[22] and power hardening law are used as the material model of aluminum alloy sheet. The viscous medium material model is considered to be rate- dependent. The finite element model of sheet and die is Belytschko-Tsay shell element, and the die is defined as rigid body. The finite element model of viscous medium is solid element.
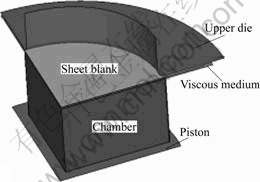
Fig. 3 Finite element modeling of VPB test
4 Results and discussion
4.1 Experimental results
Fig.4 shows the specimens obtained by viscous pressure bulging test. The fractures are along the major axes and cross the centers of specimens. The thickness strain distributions of specimens are shown in Fig.5. There are the maximal thickness strains in the center of specimens. When β=1.58, 1.3, 1.13 and 1, the minimal thicknesses at fracture position are 0.83, 0.80, 0.76 and 0.75 mm, respectively. The maximal thickness strains of specimens increase with decreasing of β. According to thickness strain distributions of specimens, it can be found that the thickness strain gradually decreases from the center to the corner.
4.2 Determination of material constant in ductile fracture criterion
The material constant is determined by the combination of the bulging test with finite element analysis. Here, the simulation is carried out for the bulging test with the elliptical die (the minor axis is 78.5 mm). When the minimum thickness of the simulated specimen reaches that of the experimental specimen, the fracture to occur is determined. The material constant is defined by substituting stress and strain values obtained from the simulation into Eqn.(1), and the calculated value is 104.2.
4.3 Forming limit prediction
The predicted forming limits of 6k21-T4 sheet obtained by VPB are shown in Fig.6. Fig.6(a) shows the distribution of Ci obtained by VPB using the elliptical die (β=1.58) in the minor axis direction at various bulging heights. The value of Ci increases with increase of bulging height. When the bulging height gets to 20.8 mm, the integral Ci at the center is equal to 1. The integral Ci gradually decreases from the center of the specimen to the corner. The distributions of values Ci of the other specimens (i.e. β=1.3, 1.13 and 1) are shown in Figs.6(b), (c) and (d), respectively. When the integral Ci at the center amounts to 1, the bulging heights of specimens are 23.6, 26.0 and 28.5 mm, respectively. According the predicted results, it can be found that the limit bulging height increases with decrease of the ratio of major axis to minor axis(β). And the fracture initiation sites and the Ci distributions of all specimens are similar. In practice, the fractures pass the centers of the bulging specimens (Fig.4). The predicted results are in good agreement with the experimental ones. The minimal thickness predicted by the combination of the numerical simulation and the

Fig.4 Viscous pressure bulging specimens: (a) β=1.58; (b) β=1.30; (c) β=1.13; (d) β=1

Fig.5 Thickness strain distributions of specimens: (a) β=1.58; (b) β=1.30; (c) β=1.13; (d) β=1
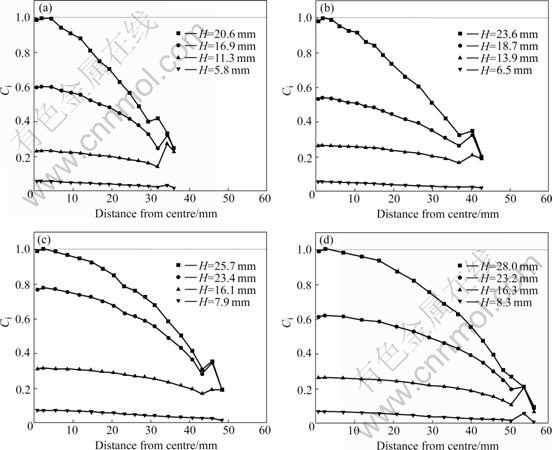
Fig.6 Distributions of Ci values of specimens: (a) β=1.58; (b) β=1.30; (c) β=1.13; (d) β=1.0
ductile fracture criterion are compared with the experimental results in Fig.7. When β=1, 1.13, 1.3 and 1.58, respectively, the minimal thicknesses of experimental specimens are 0.75, 0.76, 0.80 and 0.83 mm, and the predicted results are 0.78, 0.79, 0.80 and 0.81 mm. The difference between the predicted results and the experiment ones is less than 4%. Accordingly, the above results demonstrate that Cockroft-Latham criterion can successfully evaluate the formability of aluminum alloy sheet in finite element analysis. 5 Conclusions
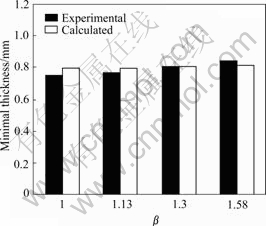
Fig.7 Comparison between calculated and experimental minimal thickness
1) Cockroft-Latham criterion fits for evaluating the viscous pressure forming limit of the aluminum alloy sheet. The material constant is determined by the combination of the viscous pressure bulging (VPB) test with finite element analysis.
2) The viscous pressure forming limits of specimens obtained in various strain paths are predicted by the ductile fracture criterion and the predicted results are in good agreement with the experimental ones.
References
[1] FRIEDMAN P A, LUCKEY S G, COPPLE W B, ALLOR R, MILLER C E, YOUNG C. Overview of superplastic forming research at Ford motor company [J]. J Mater Eng Perform, 2004, 13(6): 670-677.
[2] Liu Jun-hua, Westhoff B, Ahmetoglu M A, ALTAN T. Application of viscous pressure forming (VPF) to low volume stamping of difficult-to-form alloys: Results of preliminary FEM simulations [J]. J Mater Proc Technol, 1996, 59: 49-58.
[3] Liu Jun-hua, Ahmetoglu M, Altan T. Evaluation of sheet metal formability viscous pressure forming (VPF) dome test [J]. J Mater Proc Technol, 2000, 98: 1-6.
[4] Shulkina L B, Posterarob R A, Ahmetoglu M A, KINZEL G L, ALTAN T. Blank holder force (BHF) control in viscous pressure forming (VPF) of sheet metal [J]. J Mater Proc Technol, 2000, 98: 7-16.
[5] Wang Zhong-jin, WANG Xin-yun, WANG Zhong-ren. Viscous pressure forming (VPF) of corrugated thin-walled sheet part with small radius [J]. J Mater Proc Technol, 2004, 145: 345-351.
[6] WANG Zhong-jin, WANG Xin-yun, WANG Zhong-ren. Effect of blank holder pressure forming on aluminum alloy ladder part [J]. Trans Nonferrous Met Soc China, 2002, 12(1): 109-114.
[7] Liu Jian-guang, Wang Zhong-jin, Wang Zhong-ren. Numerical simulation of the influence of viscous adhesive stress on the viscous pressure bulging process of hemispherical sphere [J]. Trans Nonferrous Met Soc China, 2003, 13(6): 1354-1359.
[8] Marciniak Z, Kuczynski K. Limit strains in the processes of stretch-forming sheet metal [J]. Int J Mech Sci, 1967, 9: 609-20.
[9] St?ren S, Rice J R. Localized necking in thin sheets [J]. J Mech Phys Solids, 1975, 23: 421-41.
[10] Swift H W. Plastic instability under plane stress [J]. J Mech Phys Solids, 1952, 1: 1-18.
[11] Hill R. On discontinuous plastic states, with special reference to localized necking in thin sheets [J]. J Mech Phys Solids, 1952, 1: 19-30.
[12] Ozturk F, Lee D Y. Analysis of forming limits using ductile fracture criteria [J]. J Mater Proc Technol, 2004, 147: 397-404.
[13] Takuda H, Mori K, Takakura N, YAMAGUCHI K. Finite element analysis of limit strains in biaxial stretching of sheet metals allowing for ductile fracture [J]. Int J Mech Sci, 2000, 42: 785-798.
[14] Takuda H, Mori K, Fujimotoa H, Hatta N. The application of some criteria for ductile fracture to the prediction of the forming limit of sheet metals [J]. J Mater Proc Technol, 1999, 95: 116-121.
[15] Yu Zhong-qi, Lin Zhong-qin, Zhao Yi-xi. Evaluation of fracture limit in automotive aluminium alloy sheet forming [J]. Mater Des, 2007, 28: 203-207.
[16] Han H N, Kim K H. A ductile fracture criterion in sheet metal forming process [J]. J Mater Proc Technol, 2003, 142: 231-238.
[17] Takuda H, Mori K, Fujimotoa H, Hatta N. Prediction of forming limit in deep drawing of Fe/Al laminated composite sheets using ductile fracture criterion [J]. J Mater Proc Technol, 1996, 60: 291-296.
[18] Oyane M, Sato T, Okimoto K, Shima S. Criteria for ductile fracture and their applications [J]. J Mech Work Technol, 1980, 4: 65-81.
[19] Takuda H, Mori K, Fujimotoa H, Hatta N. Prediction of forming limit in bore-expanding of sheet metals using ductile fracture criterion [J]. J Mater Proc Technol, 1999, 92/93: 433-438.
[20] Jain M, Allin J, Lloyd D J. Fracture limit prediction using ductile fracture criteria for forming of an automotive aluminum sheet [J]. Int J Mech Sci, 1999, 41: 1273-1288.
[21] Cockroft M G, LATHAM D J. Ductility and workability of metals [J]. J Inst Met, 1968, 96: 33-39.
[22] Barlat F, LIAN J. Plastic behavior and stretchability of sheet metals [J]. Int J Plast, 1989, 51: 51-66.
(Edited by YANG Bing)
Corresponding author: WANG Zhong-jin; Tel: +86-451-86418643; E-mail: wangzj@hit. edu. cn