J. Cent. South Univ. (2012) 19: 562-571
DOI: 10.1007/s11771-012-1040-3
One-dimensional consolidation of double-layered soil with non-Darcian flow described by exponent and threshold gradient
LI Chuan-xun(李传勋)1, 2, XIE Kang-he(谢康和)2, HU An-feng(胡安峰)2, HU Bai-xiang(胡白香)1
1. Department of Civil Engineering, Jiangsu University, Zhenjiang 212013, China;
2. Key Laboratory of Soft Soils and Geoenvironmental Engineering of Ministry of Education, Zhejiang University,Hangzhou 310027, China
? Central South University Press and Springer-Verlag Berlin Heidelberg 2012
Abstract: Based on non-Darcian flow law described by exponent and threshold gradient within a double-layered soil, the classic theory of one-dimensional consolidation of double-layered soil was modified to consider the change of vertical total stress with depth and time together. Because of the complexity of governing equations, the numerical solutions were obtained in detail by finite difference method. Then, the numerical solutions were compared with the analytical solutions in condition that non-Darcian flow law was degenerated to Dary’s law, and the comparison results show that numerical solutions are reliable. Finally, consolidation behavior of double-layered soil with different parameters was analyzed, and the results show that the consolidation rate of double-layered soil decreases with increasing the value of exponent and threshold of non-Darcian flow, and the exponent and threshold gradient of the first soil layer greatly influence the consolidation rate of double-layered soil. The larger the ratio of the equivalent water head of external load to the total thickness of double-layered soil, the larger the rate of the consolidation, and the similitude relationship in classical consolidation theory of double-layered soil is not satisfied. The other consolidation behavior of double-layered soil with non-Darcian flow is the same as that with Darcy’s law.
Key words: one-dimensional consolidation; double-layered soil; non-Darcian flow; depth dependent vertical total stress; time- dependent loading
1 Introduction
The theory of consolidation which forecasts settlement rates and dissipation rates of excess pore-water pressure in soft clays has always been a research focus in the field of soil mechanics. As well known, Darcy’s flow law was widely applied in most existing theories of consolidation for its simplicity. However, numerous studies have shown that the water flow in fine-grained soils under low hydraulic gradients may deviate from the Darcy’s flow law [1-7]. The deviation of water flow from Darcy’s law was called as non-Darcian flow by HANSBO [1]. In addition, the non-Darcian flow proposed by HANSBO has been recognized by more researchers, and this non-Darcian flow within fine-grained soil may obey an exponential relationship at low gradients and a linear relationship at high gradients.
Since this non-Darcian flow can be recognized by many researchers, it has a theoretical significance in acquainting the influence of this non-Darcian flow law on consolidation behavior. DUBIN and MOULIN [6] firstly investigated the problem of one-dimensional consolidation with this non-Darcian flow. However, they replaced the exponential relation, v=κim, with a linear relation, v=κi, in the case of il. HANSBO [7] analyzed one-dimensional consolidation with this non-Darcian flow, and observed a better agreement to the field settlement observations. Moreover, based on this non- Darcian flow, TEH and NIE [8] analyzed the consolidation of sand-drained ground with the radial and vertical drainages and investigated the influence of non-Darcian flow on the consolidation behavior. XIE et al [9] applied a semi-analytic method to get the solution of one-dimensional consolidation equation incorporating this non-Darcian flow, but the linear flow relationship at high gradients in this non-Darcian flow was omitted. LIU et al [10] studied one-dimensional consolidation taking into consideration this non-Darcian flow by the finite volume method. E et al [11] analyzed the reason for this non-Darcian flow, and showed that the laggard dissipation of pore water pressure induced laggard rate of consolidation with this flow law. LI et al [12] made a comprehensive analysis of one-dimensional consolidation of homogeneous soil layer, taking into consideration this non-Darcian flow, along with the change of vertical total stress with depth and time together. All these previous works, however, did not deal with familiar layered soils in an actual foundation, including a double-layered soil, which is the simplest layered soil. In addition, according to the study by ZHU and YIN [13], in most cases, the consolidation of a double-layered soil occurs simultaneously with the change of vertical total stress that varies with time and depth due to a time-dependent external loading. Therefore, in this work, one-dimensional consolidation of double-layered soil was analyzed, considering the non-Darcian flow described by exponent and threshold gradient, along with the linear change of vertical total stress with depth and time together.
2 Derivation of governing equations
2.1 Presentation of problem
As shown in Fig. 1, the foundation consists of two soil layers, and an arbitrary layer is indexed with j (j=1 or 2). The water flow in both soil layers conforms to the non-Darcian flow described by exponent and threshold gradient, and the exponent and threshold gradients in the j-th layer are denoted as mj and i1j. According to the continuity conditions, i0j=i1j(mj-1)/mj and κj=kj/ 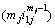 can be obtained. The coefficient of permeability, the coefficient of constrained compressibility and the coefficient of consolidation of the j-th layer are denoted as kj, mvj and cvj, respectively. The thickness of the whole double-layered soil is denoted as H, and that of the j-th soil layer is denoted as hj. Time-dependent external loading σ(0,t) is applied to the surface of double-layered soil. Drainage conditions of double-layered soil in the vertical direction are either pervious top and pervious bottom (PTPB), or pervious top and impervious bottom (PTIB).
can be obtained. The coefficient of permeability, the coefficient of constrained compressibility and the coefficient of consolidation of the j-th layer are denoted as kj, mvj and cvj, respectively. The thickness of the whole double-layered soil is denoted as H, and that of the j-th soil layer is denoted as hj. Time-dependent external loading σ(0,t) is applied to the surface of double-layered soil. Drainage conditions of double-layered soil in the vertical direction are either pervious top and pervious bottom (PTPB), or pervious top and impervious bottom (PTIB).

Fig. 1 Schematic diagram of one-dimensional consolidation of double-layered soil with non-Darcian flow
2.2 Basic assumptions
In order to get the governing equations of consolidation of a double-layered soil to consider non-Darcian flow law and linear change of vertical total stress with depth and time, the following assumptions are made:
1) Both the water and the solid constituents of the soil are perfectly incompressible;
2) The soil profile of a foundation consists of two soil layers, and the soil within each layer is homogeneous and fully saturated;
3) The deformation and the water flow within a double-layered soil only take place in the vertical direction and the small strain assumption is incorporated;
4) The soils in each layer are linearly elastic, and the coefficients of constrained compressibility are constants;
5) The water flow in the soil obeys the non-Darcian flow law described by exponent and threshold gradient, and the parameters keep constant during the process of consolidation;
6) As shown in Fig. 2, the vertical total stress within the double-layered soil is assumed to change linearly with depth within the whole soil layers and linearly increases with time up to the final value. Therefore, the vertical total stress can be expressed as
 (1)
(1)
where z and t are coordinates; s(z, t) is a function of vertical total stress; s(0, t) is the vertical total stress on time at the top surface of double-layered soil; s(H1, t) is the vertical total stress on time at z=H1; s(H, t) is the vertical total stress on time at z=H; tc is the construction time; σ0 is the value of vertical total stress at t=tc and z= 0; σ1 is the value of vertical total stress at t=tc and z=h1; σ2 is the value of vertical total stress at t=tc and z=H.
2.3 Derivation of governing equations
As shown in Fig. 1, a unit cell is taken out from the j-th soil layer of the double-layered soil. According to the continuity condition that the change of water quantity in a unit cell should be equal to the volume change of the unit cell, the differential equations governing one- dimensional consolidation of the double-layered soil with non-Darcian flow can be derived, considering variation of vertical total stress with depth and time:
 (2)
(2)
where 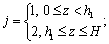 uj(z, t) is excess pore water
uj(z, t) is excess pore water
pressure in the j-th soil layer; ij(z, t) is the hydraulic gradient in the j-th soil layer.
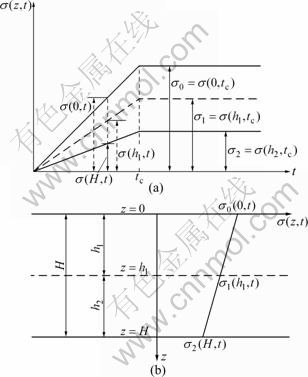
Fig. 2 Variations of vertical total stress with time (a) and depth (b)
Two common drainage conditions in the vertical direction, either pervious top and pervious bottom (PTPB), or pervious top and impervious bottom (PTIB), can be written as
 (PTIB) (3a)
(PTIB) (3a)
 (PTPB) (3b)
(PTPB) (3b)
Continuity conditions of excess pore water pressure and flow velocity between different soil layers can be expressed as
 (4a)
(4a)
 (4b)
(4b)
where i1(h1, t) is the hydraulic gradient of the first soil layer at z=h1; i2(h1, t) is the hydraulic gradient of the second soil layer at z=h1.
The initial condition can be further given as
 (5)
(5)
3 Derivation of numerical solutions
3.1 Governing equation in terms of dimensionless variables
In order to simplify the process of calculation, the dimensionless variables are introduced as follows:




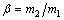









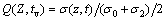


 (6)
(6)
where j=1 or 2.
In terms of these dimensionless variables, the governing Eq. (2) can be rewritten as
 (7)
(7)
where

 (8)
(8)
In terms of aforementioned dimensionless variables, Eqs. (3a), (3b), (4a), (4b) and (5) can be rewritten as
 (PTIB) (9a)
(PTIB) (9a)
 (PTPB) (9b)
(PTPB) (9b)
 (10a)
(10a)
 (10b)
(10b)
 (11)
(11)
3.2 Discretization of governing equation
Equation (7) is a second order non-linear differential equation, and analytical solutions can hardly be obtained. Therefore, finite differential method is adopted to get numerical solutions of excess pore water pressure and average degree of consolidation. Firstly, the spatial domain within the first soil layer, 0≤Z≤Zf, is divided into N1 equant segments from the top down by the proportional spacing ΔZ, and the second soil layer is divided by the proportional spacing ΔZ into N2 equant segments. If the spatial nodal points are denoted as Zl, there is
Zl=lΔZ, l=1, 2, 3, …, N1, N1+1, …, N (12)
where N=N1+N2.
At the same time, the time domain is divided into numerous time increment Δtvk. If the nodal points of time domain is denoted as tvk, there is
tvk=∑Δtvk, k=0, 1, 2, 3, … (13)
Thus, a finite differential grid has been placed in the (Z,tv)-plane. The Crank-Nicolson difference scheme is adopted for its relative stability. In terms of Crank- Nicolson difference scheme, the governing Eq. (7) can be expressed as

 (14)
(14)
where  ; k=0, 1, 2, 3, …;
; k=0, 1, 2, 3, …;  is
is
dimensionless expression for excess pore water pressure of the j-th soil layer at Z=lΔZ and tv =tvk; 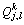 is dimensionless expression for vertical total stress of the j-th soil layer at Z=lΔZ and tv =tvk.
is dimensionless expression for vertical total stress of the j-th soil layer at Z=lΔZ and tv =tvk.
λ=(Δtv)/(ΔZ)2



In terms of discrete points in the differential grid, drainage and continuity conditions can be rewritten as
 (PTIB) (15a)
(PTIB) (15a)
 (PTPB) (15b)
(PTPB) (15b)
 (16a)
(16a)
 (16b)
(16b)
In terms of matrix, the difference of Eq. (14) in drainage condition and continuity conditions can be rewritten as
 (17)
(17)
According to the difference of Eq. (14), the elements of matrices A and B can be expressed as
 (18a)
(18a)
 (18b)
(18b)

 (18c)
(18c)
where l=1, 2, …, N1-1, N1+1, …, N-1.
According the flow continuity condition at the interface of different soil layers,  and
and  can be written as
can be written as
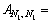

 (19a)
(19a)

 (19b)
(19b)

 (19c)
(19c)
 (19d)
(19d)
For the case of PTIB, it can be seen from Eq. (7) that mathematical calculation difficulties with non-Darcian flow law may be encountered at the bottom boundary surface for its imperviousness. Since both Darcy’s flow law and non-Darcian flow pass through the original, Darcy’s flow law is equivalent to this non-Darcian flow law at the impervious boundary. In order to get rid of the mathematical calculation difficulties, Darcy’s flow law should be adopted at the impervious boundary. So, AN,N, AN,N-1 and BN can be expressed as
AN,N=-2(1+λ) (20a)
AN,N-1=2λ (20b)
 (20c)
(20c)
For the case of PTPB, according to Eq. (15b), AN,N, AN,N-1 and BN should be expressed as
AN,N=1 (21a)
AN,N-1=0 (21b)
BN=0 (21c)
U is an unknown column matrix, and its elements 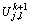 are dimensionless expressions of excess pore water pressure at tv,k+1. B is a known column matrix, and its elements can be expressed by the dimensionless variables of excess pore water pressure at tv,k. In order to obtain the unknown column matrix U, matrix A should be a constant matrix. If a time increment is little enough, replacing the dimensionless value of excess pore water pressure at tv,k+1 by that at tv,k can be allowed, and approximation for matrix U could be obtained by solving Eq. (17). Moreover, the exact solutions for matrix U can be obtained by iterations, i.e. repeating the above solving scheme. According to the study by ELNAGGAK and KRIZEK [14], the solving conditions of Eq. (17) during the process of iterations can be satisfied.
are dimensionless expressions of excess pore water pressure at tv,k+1. B is a known column matrix, and its elements can be expressed by the dimensionless variables of excess pore water pressure at tv,k. In order to obtain the unknown column matrix U, matrix A should be a constant matrix. If a time increment is little enough, replacing the dimensionless value of excess pore water pressure at tv,k+1 by that at tv,k can be allowed, and approximation for matrix U could be obtained by solving Eq. (17). Moreover, the exact solutions for matrix U can be obtained by iterations, i.e. repeating the above solving scheme. According to the study by ELNAGGAK and KRIZEK [14], the solving conditions of Eq. (17) during the process of iterations can be satisfied.
3.3 Solutions of degree of consolidation
The average degree of consolidation in terms of deformation Ust can be defined as
 (22)
(22)
The deformation of double-layered soil at any time St follows

 (23)
(23)
The final settlement of double-layered soil S∞ can be written as
 (24)
(24)
Substituting Eqs. (23) and (24) into Eq. (22), in terms of dimensionless variables, the following equation can be obtained:
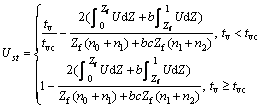 (25)
(25)
Since the analytical solution of excess pore water pressure can not be derived, numerical integration must be introduced to Eq. (25). In terms of numerical integration, Eq. (25) can be expressed as
 (26)
(26)
The definition of average degree of consolidation in terms of stress (or excess pore water pressure) is the ratio of average effective stress at any time to average final effective stress in double-layered soil:
 (27)
(27)
If dimensionless variables and numerical integration are incorporated, Eq. (27) can be rewritten as
 (28)
(28)
It can be seen from Eqs. (26) and (28) that average degree of consolidation in terms of deformation is equal to that in terms of stress at the case of b=1. Otherwise, average degree of consolidation in terms of deformation is not equal to that in terms of stress for the case of PTIB. That is, for double-layered soil, the dissipation rate of excess pore water pressure is usually not equal to the rate of deformation any more.
4 Verification of difference results
Based on Darcy’s law, XIE [15] gave a general analytical solution to the problem of one-dimensional consolidation for a double-layered soil with arbitrary distribution of initial pore water pressure and casual variation of surface load with time, and ZHU and YIN [13] presented an analytical solution for the consolidation analysis of a double-layered soil profile under depth-dependent ramp loading. When the equation m1=m2=1 is satisfied, non-Darcian flow in the double- layered soil can be degenerated into Darcy’s law. Thus, the theory of consolidation of double-layered soil with non-Darcian flow law will be turned into Darcy’s law. Table 1 gives a comparison between the results by FDM and that by analytical method at the case of m1=m2=1. It can be seen that the maximum value of absolute error of average degree of consolidation is 0.531 7%, and corresponding relative error is 0.84%. Therefore, the results of average degree of consolidation by FDM can be supposed to be consistent with the analytical solutions, and the reliability of difference program is verified.
5 Consolidation behavior of double-layered soil with non-Darcian flow
It can be seen from solution procedure that influencing factors of double-layered consolidation with non-Darcian flow include parameters of non-Darcian flow, relative permeability and relative compressibility of double-layered soil, the ratio of the equivalent water head of external load to the thickness of double-layered soil, uniform distribution of vertical total stress and ramp loading rate. Then, PTIB is taken from drainage conditions as an example to explain consolidation behavior of double-layered soil.
5.1 Influence of non-Darcian flow law on consolidation behavior of double-layered soil
LI et al [12] analyzed consolidation behavior of homogeneous soil with non-Darcian flow described by exponent and threshold gradient, and indicated the influence of non-Darcian flow on consolidation behavior. The lager the exponent and threshold gradient of non-Darcian flow, the little the rate of consolidation for homogeneous soil. Figures 3 and 4 show the influence of the exponent and threshold gradient on consolidation behavior of double-layered soil. The consolidation rate of Case 1 is larger than that of other cases, and that of Case 4 is the lowest. Thus, for double-layered soil, the smaller the exponent and threshold gradient, the larger the consolidation rate. Meanwhile, the exponent and threshold gradient of the first soil layer greatly influence the consolidation rate of double-layered soil for the case of PTIB.
5.2 Influence of permeability and compressibility of double-layered soil on consolidation behavior
For homogeneous soil with non-Darcian flow, if the parameters of non-Darcian flow are considered constant, coefficient of consolidation is a unique soil indicator deciding consolidation rate, and it is unnecessary to consider permeability and compressibility of soil layers. For double-layered soil, however, such position of consolidation coefficient is no longer satisfied. As shown in Fig. 5, even if consolidation coefficients of both soil layers with different permeability and compressibility are the same, the rate of deformation is no longer equivalent. Thus, consolidation behavior of double-layered soil largely depends on relative permeability, the value of a, and relative compressibility, the value of b. Such consolidation behavior of double- layered soil is consistent with that based on Darcy’s flow law.
Table 1 Comparison between results by FDM and analytic solutions


Fig. 3 Influence of exponent on average degree of consolidation in terms of deformation (Case 1: m1=1.2, m2=1.2; Case 2: m1= 1.2, m2=1.5; Case 3: m1=1.5, m2=1.2; Case 4: m1=1.5, m2=1.5)

Fig. 4 Influence of threshold gradient on average degree of consolidation in terms of deformation (Case 1: i11=5, i12=5; Case 2: i11=5, i12=20; Case 3: i11=20, i12=5; Case 4: i11=20, i12=20)

Fig. 5 Curve of average degree of consolidation in double- layered soils with different permeability and compressibility
Figure 6 shows that the consolidation rate of double-layered soil decreases with the increase of the thickness of low-permeability and high-compressibility soil layer, and increases with the increase of the thickness of high-permeability and low-compressibility soil layer. Therefore, based on non-Darcian flow, replacing soft soil with high-permeability and low-compressibility materials in actual engineering not only decreases the total settlement, but also accelerates the consolidation of soil. This consolidation behavior of double-layered soil is the same as that with Darcy’s law.

Fig. 6 Influence of relative thickness of double-layered soil on average degree of consolidation
It can be seen from Fig. 7 that the average degree of consolidation in terms of deformation is not equal to that in terms of stress except the case of b=1. If b is not equal to one, the dissipation rate of excess pore water pressure of double-layered soil is not consistent with deformation rate. This consolidation behavior of double-layered soil with non-Darcian flow is different from that of homogeneous soil with non-Darcian flow, but is the same as that of double-layered soil with Darcy’s flow.

Fig. 7 Comparison of average degree of consolidation in terms of stress and in terms of deformation (Case 1: a=10, b=10; Case 2: a=1, b=1; Case 3: a=0.1, b=0.1)
5.3 Influence of external load and thickness of double- layered soil on consolidation behavior
Influence of qh on consolidation behavior can be seen from Fig. 8. The larger the value of qh, the faster the consolidation. In addition, the curve of consolidation with non-Darcian flow can gradually approach that with Darcy’s flow with the increase of the value of qh. The value of qh is the ratio of the equivalent water head of external load to the total thickness of double-layered soil. The consolidation rate of the double-layered soil with different ratios of the equivalent water head of external load to the thickness will be different, even if at the same time factor. Therefore, influences of external load and the thickness of double-layered soil are the same as those of homogeneous soil with non-Darcian flow. The similitude relationship between thin samples and field layers with non-Darcian flow is no longer satisfied.

Fig. 8 Influence of qh on average degree of consolidation in terms of deformation
5.4 Influence of uniform distribution of vertical total stress on consolidation behavior
Figure 9 shows the influence of uniform distribution of vertical total stress on average degree of consolidation. The consolidation rate of Case 1 is faster than that of other cases, and the consolidation in terms of deformation accelerates with the increase of the value of n0. Case 1 indicates that vertical total stress decreases from maximum with increasing the depth of soil layers, naming reverse triangle distribution. Case 5 indicates that vertical total stress increases from zero with the increase of depth of soil layers, naming triangle distribution. Therefore, for the case of PTIB, the rate of consolidation is at its maximum for the case of reverse triangle distribution of vertical total stress while at its minimum for the case of triangle distribution. This consolidation behavior of double-layered soil is the same as that with Darcy’s law.
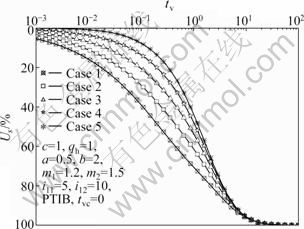
Fig. 9 Influence of uniform distribution of vertical total stress on average degree of consolidation in terms of deformation (Case 1: n0=2, n1=1, n2=0; Case 2: n0=1.5, n1=1, n2=0.5; Case 3: n0=1, n1=1, n2=1; Case 4: n0=0.5, n1=1, n2=1.5; Case 5: n0=0, n1=1, n2=2)
5.5 Influence of loading rate on consolidation behavior
Figure 10 shows the influence of loading rate on average degree of consolidation in terms of deformation. tvc=0 indicates that the external load is instantly applied to the surface of double-layered soil, and the rate of deformation is larger than other values of tvc. Therefore, the rate of deformation decreases with the increase of the value of construction time factor, tvc. This consolidation behavior of double-layered soil is the same as that with Darcy’s law.

Fig. 10 Influence of loading rate on average degree of consolidation in terms of deformation
6 Conclusions
1) The consolidation rate of double-layered soil decreases with the increase of the value of exponent and threshold of non-Darcian flow, and the exponent and threshold gradients of the first soil layer greatly influence the consolidation rate of double-layered soil. Even if the parameters of non-Darcian flow keep constant, coefficient of consolidation is not a unique soil indicator deciding the consolidation behavior of double-layered soil any more. Relative permeability and relative stiffness of double-layered soil greatly influence the rate of consolidation.
2) In condition that the stiffness of soil layers is not equivalent, for double-layered soil, the average degree of consolidation in terms of deformation is no longer equal to that in terms of stress. The dissipation rate of excess pore water pressure is not equal to the rate of deformation.
3) Based on non-Darcian flow, the larger the ratio of the equivalent water head of external load to the total thickness of double-layered soil, the faster the consolidation, and the similitude relationship between thin samples and field layers under non-Darcian flow is not satisfied. The rate of consolidation of double-layered soil decreases with the increase of the thickness of low-permeability and high-compressibility soil layer, and increases with the increase of the thickness of high- permeability and low-compressibility soil layer.
4) Distribution of vertical total stress is closely related to the consolidation rate of double-layered soil. For the case of PTIB, the rate of consolidation is at its maximum for the case of reverse triangle distribution of vertical total stress. The less the value of construction time factor, the faster the deformation of double-layered soil.
References
[1] HANSBO S. Consolidation of clay with special reference to influence of vertical drains [C]// Proceedings of Swedish Geotechnical Institute. Stockholm: Swedish Geotechnical Institute, 1960, 18: 45-50.
[2] SWARTZENDRUBER D. Modification of Darcy’s law for the flow of water in soils [J]. Soil Science, 1962, 93(1): 22-29.
[3] MILLER R J, LOW P E. Threshold gradient for water flow in clay systems [J]. Soil Science Society of American Journal, 1963, 27(6): 605-609.
[4] OLSEN H W. Osmosis: A cause of apparent deviation from Darcy’s law [J]. Canadian Geotechnical Journal, 1985, 22(2): 238-241.
[5] HANSBO S. Aspects of vertical drain design: Darcian or non-Darcian flow [J]. Geotechnique, 1997, 47(5): 983-992.
[6] DUBIN B, MOULIN G. Influence of a critical gradient on the consolidation of clays [C]// Consolidation of soils: testing and evaluation, ASTM STP 892. West Conshohocken (PA): American Society for Testing and Materials, 1986: 354-377.
[7] HANSBO S. Deviation from Darcy’s law observed in one-dimensional consolidation [J]. Geotechnique, 2003, 53(6): 601-605.
[8] TEH C I, NIE X Y. Coupled consolidation theory with non-Darcian flow [J]. Computers and Geotechnics, 2002, 29(3): 169-209.
[9] XIE Hai-lan, WU Qiang, ZHAO Zeng-min, JIN Xiao-li, LI Juan. Consolidation computation of aquitard considering non-Darcy flow [J]. Rock and Soil Mechanics, 2007, 28(5): 1061-1065. (in Chinese)
[10] LIU Zhong-yu, SUN Li-yun, YUE Jin-chao, MA Chong-wu. 1D consolidation theory of saturated clay based on non-Darcy flow [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 973-979. (in Chinese)
[11] E Jian, CHEN Gang, SUN Ai-rong. One-dimensional consolidation of saturated cohesive soil considering non-Darcy flows [J]. Chinese Journal of Geotechnical Engineering, 2009, 31(7): 1115-1119. (in Chinese))
[12] LI Chuan-xun, XIE Kang-he, WANG Kun. Analysis of 1D consolidation with non-Darcian flow described by exponent and threshold gradient [J]. Journal of Zhejiang University: Science A (Applied Physics & Engineering), 2010, 11(9): 656-667.
[13] ZHU G., YIN J H. Consolidation of double soil layers under depth-dependent ramp load [J]. Canadian Geotechnical Journal, 1999, 49(3): 415-421.
[14] ELNAGGAK H A, KRIZEK R J. Effect of non-Darcy flow on time rate of consolidation [J]. Journal of the Franklin Institute, 1973, 296(5): 323-337.
[15] XIE Kang-he. Theory of one dimensional consolidation of double-layered ground and its application [J]. Chinese Journal of Geotechnical Engineering, 1994, 16(5): 24-35. (in Chinese)
(Edited by HE Yun-bin)
Foundation item: Projects(50878191, 51109092) supported by the National Natural Science Foundation of China
Received date: 2011-01-14; Accepted date: 2011-04-06
Corresponding author: XIE Kang-he, PhD; Tel: +86-571-87951339; E-mail: zdkhxie@zju.edu.cn