Transient analysis of Casson fluid thermo-convection from a vertical cylinder embedded in a porous medium: Entropy generation and thermal energy transfer visualization
来源期刊:中南大学学报(英文版)2019年第5期
论文作者:JANARDHANA REDDY G BHASKERREDDY Kethireddy MAHESH Kumar ANWAR BEG O
文章页码:1342 - 1361
Key words:vertical cylinder; entropy generation; Casson fluid; finite difference method; heat function; porous medium
Abstract: Thermal transport in porous media has stimulated substantial interest in engineering sciences due to increasing applications in filtration systems, porous bearings, porous layer insulation, biomechanics, geomechanics etc. Motivated by such applications, in this article, a numerical study of entropy generation impacts on the heat and momentum transfer in time-dependent laminar incompressible boundary layer flow of a Casson viscoplastic fluid over a uniformly heated vertical cylinder embedded in a porous medium is presented. Darcy’s law is used to simulate bulk drag effects at low Reynolds number for an isotropic, homogenous porous medium. Heat line visualization is also included. The mathematical model is derived and normalized using appropriate transformation variables. The resulting non-linear time-dependent coupled governing equations with associated boundary conditions are solved via an implicit finite difference method which is efficient and unconditionally stable. The outcomes show that entropy generation and Bejan number are both elevated with increasing values of Darcy number, Casson fluid parameter, group parameter and Grashof number. To analyze the heat transfer process in a two-dimensional domain, plotting heat lines provides an excellent approach in addition to streamlines and isotherms. It is remarked that as the Darcy number increases, the deviations of heat lines from the hot wall are reduced.
Cite this article as: JANARDHANA REDDY G, BHASKERREDDY Kethireddy, MAHESH Kumar, ANWAR B G O. Transient analysis of Casson fluid thermo-convection from a vertical cylinder embedded in a porous medium: Entropy generation and thermal energy transfer visualization [J]. Journal of Central South University, 2019, 26(5): 1342–1361. DOI: https://doi.org/10.1007/s11771-019-4091-x.
G O. Transient analysis of Casson fluid thermo-convection from a vertical cylinder embedded in a porous medium: Entropy generation and thermal energy transfer visualization [J]. Journal of Central South University, 2019, 26(5): 1342–1361. DOI: https://doi.org/10.1007/s11771-019-4091-x.

J. Cent. South Univ. (2019) 26: 1342-1361
DOI: https://doi.org/10.1007/s11771-019-4091-x
JANARDHANA REDDY G1, BHASKERREDDY Kethireddy1, MAHESH Kumar1, ANWAR B G O2
G O2
1. Department of Mathematics, Central University of Karnataka, Kalaburagi, 585367, India;
2. Fluid Mechanics, Aeronautical and Mechanical Engineering Department, School of Computing,
Science and Engineering, University of Salford, Manchester M54WT, UK
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Thermal transport in porous media has stimulated substantial interest in engineering sciences due to increasing applications in filtration systems, porous bearings, porous layer insulation, biomechanics, geomechanics etc. Motivated by such applications, in this article, a numerical study of entropy generation impacts on the heat and momentum transfer in time-dependent laminar incompressible boundary layer flow of a Casson viscoplastic fluid over a uniformly heated vertical cylinder embedded in a porous medium is presented. Darcy’s law is used to simulate bulk drag effects at low Reynolds number for an isotropic, homogenous porous medium. Heat line visualization is also included. The mathematical model is derived and normalized using appropriate transformation variables. The resulting non-linear time-dependent coupled governing equations with associated boundary conditions are solved via an implicit finite difference method which is efficient and unconditionally stable. The outcomes show that entropy generation and Bejan number are both elevated with increasing values of Darcy number, Casson fluid parameter, group parameter and Grashof number. To analyze the heat transfer process in a two-dimensional domain, plotting heat lines provides an excellent approach in addition to streamlines and isotherms. It is remarked that as the Darcy number increases, the deviations of heat lines from the hot wall are reduced.
Key words: vertical cylinder; entropy generation; Casson fluid; finite difference method; heat function; porous medium
Cite this article as: JANARDHANA REDDY G, BHASKERREDDY Kethireddy, MAHESH Kumar, ANWAR B G O. Transient analysis of Casson fluid thermo-convection from a vertical cylinder embedded in a porous medium: Entropy generation and thermal energy transfer visualization [J]. Journal of Central South University, 2019, 26(5): 1342–1361. DOI: https://doi.org/10.1007/s11771-019-4091-x.
G O. Transient analysis of Casson fluid thermo-convection from a vertical cylinder embedded in a porous medium: Entropy generation and thermal energy transfer visualization [J]. Journal of Central South University, 2019, 26(5): 1342–1361. DOI: https://doi.org/10.1007/s11771-019-4091-x.
1 Introduction
Natural convection boundary layer flows external to various bodies constitute a major area of interest in thermofluid dynamics. Geometries may include cylinders, ellipses, spheres, curved walls, wavy plates, cones, etc. These feature frequently in industrial manufacturing and process engineering systems. The thermal buoyancy force associated with natural convection flows can exert a critical role in determining wall shear stress and heat transfer rates at the boundary. The popularity of cylindrical bodies in thermal engineering has motivated an exceptional interest in analysing the free convection boundary layer flows from cylinders. SPARROW et al [1] were among the first researchers to investigate free convective fluid flow adjacent to the vertical cylinder with asymptotic methods. LEE et al [2] extended the model in Ref. [1] to the non-isothermal case for a thin vertical cylinder. These investigations were however restricted to Newtonian viscous flows, i.e., they did not consider rheological effects which characterize numerous working fluids and complex materials for example polymer processing operations. In the past several decades, non- Newtonian transport phenomena have motivated considerable interest among engineers, physicists, and mathematicians. This area presents a rich spectrum of nonlinear boundary value problems largely due to the extremely diverse range of rheological models available for simulating complex flow behavior. Popular non-Newtonian models include viscoelastic models, shear-thinning fluids, viscoplastic models and polar fluid models. A particular group of viscoplastic fluids is quite accurately simulated with the Casson model. These include gels, foodstuffs, blood, certain polymers under shear rates (due to the existence of fibrinogen, protein, and globulin in aqueous base plasma substances) [3] and also paints and inks. The Casson model fits the rheological data of many real working fluids more closely than alternative viscoplastic models (e.g., Bingham model). Casson fluids are “shear thinning liquids which are assumed to have an infinite viscosity at zero rate of shear, a yield stress below which no flow occurs and zero viscosity at an infinite rate of shear [4]”. The Casson fluid model was originally introduced to represent pigment-oil suspensions in printing ink [5].Owing to the applicability of this model also in polymer sheet processing, several researchers [6, 7] investigated heat transfer Casson fluid flow problem for stretching sheet/surface geometries by considering various conditions. The time-dependent flow of a Casson fluid from a plate and cone with radiation heat flux and chemical reaction effects was examined by MYTHILI et al [8]. Time- dependent magnetic Casson boundary layer flow from a plate with chemical reaction and radiation was examined by DAS et al [9]. NADEEM et al [10] studied analytically for hydromagnetic Casson fluid flow from a sheet. RAJU et al [11] analyzed the wall blowing/suction effects on Casson fluid flow from a stretching heat surface with mass transfer.
Entropy generation minimization (EGM) has emerged as a fundamental modern technique for designing thermal systems. EGM assists the engineer in identifying which procedure, system or installation is the most efficient, and it has been deployed in many sophisticated areas including electric cooling, energy systems, combustion, refrigeration, and materials processing. Some recent entropy generation minimization applications include design of pseudo-optimization processes for solar heat exchangers [12], reducing lost obtainable work during processes of heat transfer [13] and multi-field flows [14]. Further studies include Refs. [15–17] in which entropy generation was conducted for several flow formations. MAHIAN et al [18] considered the entropy analysis in the thermal flow of electrically-conducting fluids flanked by two isothermal cylinders with different wall conditions in the occurrence of a magnetic field. Analysis of thermodynamic for fluid flows for rotating cylinders was reported in [19–21]. JIA et al [22] examined the concept of entropy generation in MHD Casson nanofluid convection flow past a porous surface.
Fluid dynamics in porous media arises in widespread applications including thermal insulation systems, filtration, chemical reactor design, contaminant dispersion in soils, tissue biophysics, etc. Hydrodynamics of “non-Newtonian fluids in porous media” with and without heat transfer features in chemical engineering packed beds, gel manufacture, viscous fingering in geological transport (gas and oil flow in reservoirs), digestive transport in physiology and also tribological bearings. A popular approach is to simulate bulk porous matrix drag effects with the classical Darcy law which is valid for viscous dominated flows (low Reynolds numbers) wherein inertial effects are negated. Casson viscoplastic transport in porous media has also stimulated some attention. ASMA et al [23] studied the transient MHD flow of Casson fluid through a porous medium over a vertical plate. RAMACHANDRA et al [24] analyzed the heat-transfer characteristics in thermal convection of Casson fluids through non-Darcy porous media engulfing a horizontal cylinder. The transient flow of MHD Casson fluid with chemical-reaction effects was analysed by HARI et al [25].
Thus far, a relatively limited number of works have been directed towards physico-mathematical modeling of Casson fluid flow and heat transfer from a vertical cylinder in porous media with entropy heat generation. The present study is therefore concentrated on applying second law thermodynamic analysis to thermal convection in viscoplastic boundary layer flow of a Casson fluid adjacent to the isothermal vertical cylinder embedded in a Darcian porous media. Additionally, it is worth to study the heatlines along with streamlines and isotherms. KIMURA et al [26] and BEJAN [27] introduced the concept of heatline flow visualization. For a cylindrical geometry, RANI et al [28] studied the heatlines for non-Newtonian fluid. Subsequently, they analyzed the visualization of massline for the same geometry [29]. The deployment of the heat lines approach for convection problems is further elucidated in Ref. [30]. Thus far, the heat line visualization approach has not been employed widely in heat transfer simulations for non- Newtonian fluids. The current work presents for the first time “accurate and detailed visualization of Casson viscoplastic heat transfer flow from an isothermal vertical cylinder with entropy generation using this heat function concept”.
The present article is organized in succeeding ways: Section 2 describes the mathematical transport model and its non-dimensionalisation. Section 3 presents Crank-Nicolson numerical finite difference solutions and grid generation aspects. Section 4 includes extensive computational results (via graphs) for the time-dependent 2-D flow-field profiles. This section also includes the heat function derivation and its normalization. Extensive discussion is also presented. Lastly, in Section 5 key findings are summarized and possible extensions to the investigation are described.
2 Mathematical modelling
Time-dependent, 2-D, laminar incompressible Casson viscoplastic fluid flow from a cylinder of radius r0, embedded in a porous medium, is considered, as illustrated in Figure 1. A cylindrical coordinate scheme is adopted in which axes (x-axis and r-axis) are orientated along the length of the cylinder and radially from the origin point at the base. The neighboring fluid temperature is constant and alike to that prescribed for the ambient temperature T′∞. At the beginning, i.e., t′=0, the temperature T′∞ is identical for the vertical cylinder and neighboring fluid. Soon after (t′>0), the vertical cylinder temperature is amplified to T′w(>T′∞) and conserved consistently thereafter.
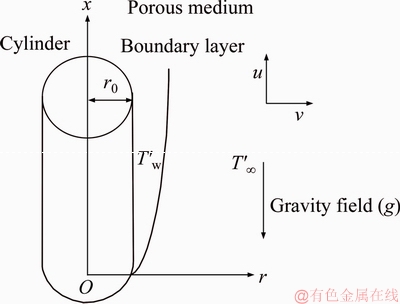
Figure 1 Schematic of investigated problem
The rheological model presents the convection flow of Casson fluid and is given by [5]:
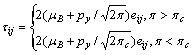 (1)
(1)
The symbols featured in Eq. (1) is explained in Ref. [31]. Implementing the Boussinesq approximation (linear variation in density), the appropriate “conservation for continuity, momentum and heat-transfer governing equations for thermal free convective boundary layer flow of a Casson fluid in a Darcian porous medium” assume the form [32, 33]:
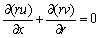 (2)
(2)
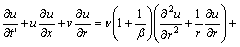
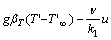 (3)
(3)
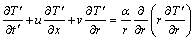 (4)
(4)
The associated initial and boundary conditions are given by
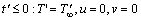
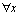 and r;
and r;
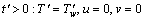 at
at 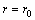 ;
;
 at x=0;
at x=0;
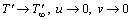 as
as 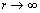 (5)
(5)
where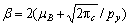 is the Casson viscoplastic parameter.
is the Casson viscoplastic parameter.
Invoking the following non-dimensional quantities:
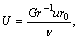
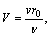
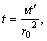
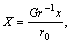
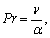
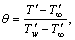

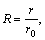
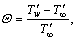
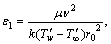
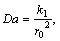
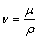 (6)
(6)
(the description of symbols mentioned in the nomenclature) in Eqs. (2)–(4) and (5), the unsteady boundary layer equations reduce to the following form:
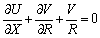 (7)
(7)
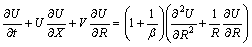 +
+
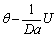 (8)
(8)
 (9)
(9)

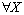 and R;
and R;
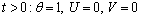 at R=1;
at R=1;
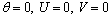 at X=0;
at X=0;
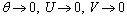 as
as 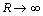 (10)
(10)
3 Finite difference numerical solutions
Analytical solutions of the time-dependent Eqs. (7)–(9) are intractable. A computational approach is therefore selected based on the “Crank-Nicolson finite difference iteration scheme which is unconditionally stable”. The finite difference discretized versions of Eqs. (7)–(9) take the form:
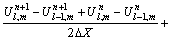
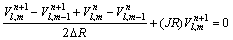 (11)
(11)
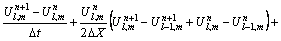

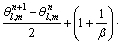
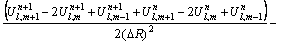
 (12)
(12)

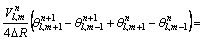
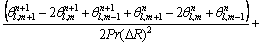
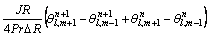 (13)
(13)
where 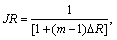 l, m are the grid levels and n denotes time step level.
l, m are the grid levels and n denotes time step level.
The above coupled finite difference non-linear equations are solved on a rectangular grid with “Xmax=1, Xmin=0, Rmax=20 and Rmin=1,” where Rmax correlates to R=∞ which keeps distant from the thermal and hydrodynamic boundary layers. For a complete explanation of this finite difference procedure the reader can refer to RANI et al [34].
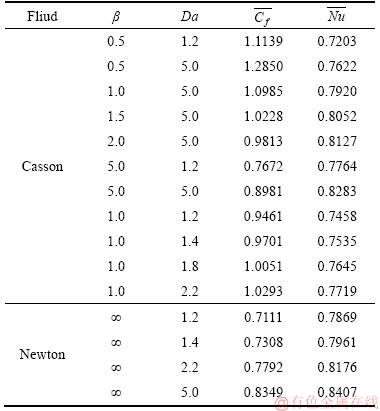
To achieve an efficient and reliable grid system for the simulations, “a grid independency test” is done for distinct grid sizes of 25×125, 50×250, 100×500 and 200×1000. The values of 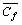 and
and 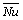 on the cylindrical boundary R=1 are presented in Table 1. A consistent grid is applied for all cases. It is perceived from Table 1 that the 100×500 grid compared with 50×250 and 200×1000 grids does not noticeably modify the results for
on the cylindrical boundary R=1 are presented in Table 1. A consistent grid is applied for all cases. It is perceived from Table 1 that the 100×500 grid compared with 50×250 and 200×1000 grids does not noticeably modify the results for 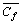 and
and 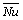 . Hence consistent with this remark, a unique grid size of 100×500 is of adequate accuracy for the current problem with the grid stepping distances of 0.03 and 0.01 in R and X directions, respectively. In the same way, to calculate efficient result pertaining to time, a time-independent test is done for distinct time step sizes and is summarized in Table 2. The effective time step size Δt (t=nΔt, n=0, 1, 2, …) is set as 0.01.
. Hence consistent with this remark, a unique grid size of 100×500 is of adequate accuracy for the current problem with the grid stepping distances of 0.03 and 0.01 in R and X directions, respectively. In the same way, to calculate efficient result pertaining to time, a time-independent test is done for distinct time step sizes and is summarized in Table 2. The effective time step size Δt (t=nΔt, n=0, 1, 2, …) is set as 0.01.
4 Results and discussion
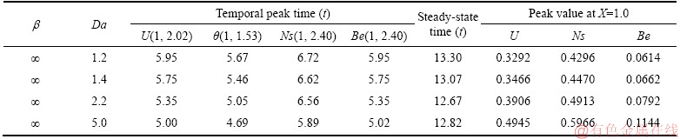
To analyse the unsteady nature of the key variables, i.e., “velocity and temperature”, computations are presented at a representative location near the cylindrical wall. The computed variables for the Newtonian fluid case without porous medium (β=∞) are analogous with previous results given by LEE et al [2] for “Prandtl number (Pr)=0.7” and are shown in Figure 2. Generally, close correlation is achieved which corroborates the validity and accuracy of the present numerical method. The outcomes are denoted to explain the nature flow variables, stream and heat functions, average wall shear stress and Nusselt number which are studied along with “entropy generation number (Ns) and Bejan number (Be)” for different thermophysical control parameters. The Darcy number (Da) denotes the relative effect of the permeability of the medium to the cross-sectional area. When Darcy number is high (i.e., Da>1), the influence of viscous forces is important and slows down the convective motion in porous media, which results in lower heat transfer. On the other hand, for Da>1 reproduces the clear fluid limit with a high degree of accuracy. When Darcy number is small (Da<1), the viscous effect becomes smaller and it can be said to be negligible. In view of the above physical explanation, the authors have chosen the Da>1 values in this manuscript to simulate high-permeability media which feature in filtration materials in industry.
Table 1 Grid independence test for selecting mesh size
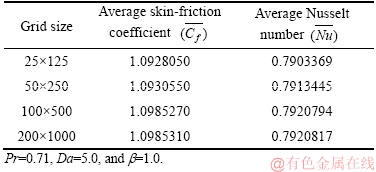
Table 2 Time independence test for selecting time step size
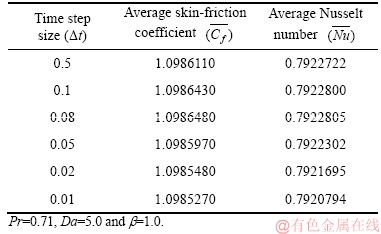
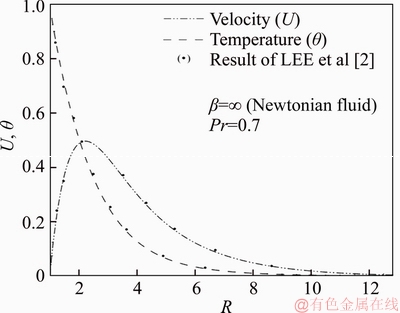
Figure 2 Comparison of velocity and temperature profiles
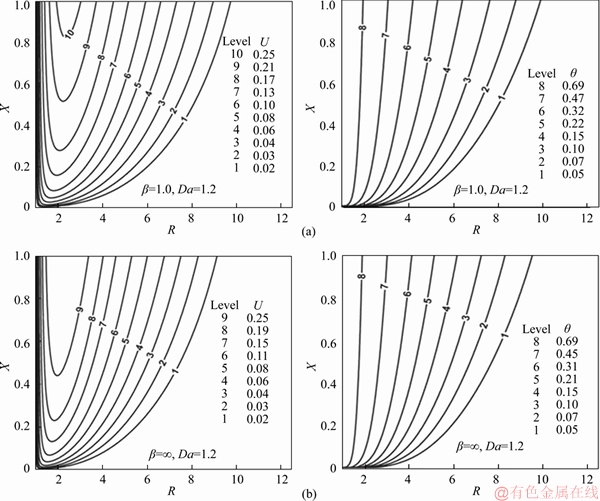
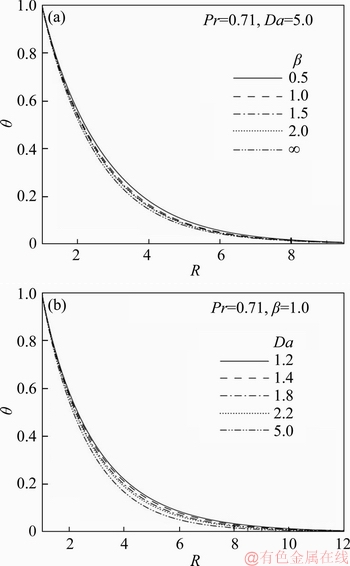
4.1 Flow variables
Figure 3 demonstrates the unsteady graph for velocity (U) profiles against t at the spatial coordinate (1, 2.02) for certain values of non-dimensional Casson fluid parameter (β) and Darcy number (Da). Figure 3(a) displays the unsteady nature of velocity curves for distinct β values with Da=5 and Figure 3(b) for values of Da with β=1. From Figures 3(a) and (b), the behavior of velocity is identified that initially, it is enhanced with time (i.e., boundary layer flow acceleration), reaches the temporal maxima, and then declines and at the end it becomes asymptotic steady. For example, in Figure 3(a) when β=1.0 and Da=5, with t, the velocity at the wall intensifies consistently, reaches the temporal peak and finally, achieves the asymptotic steady-state. Further, it is noticed that for small interval of time, the effect of heat transfer is conquered by conduction (t<<1). Consequently, there arises a time phase where “the heat transfer rate” is affected by the result of free convection and this accelerates the Casson fluid flow pertaining to time. Soon after, before achieving the time- independent state, overshoot is found for velocity curves. Also, Figure 3(a) shows that firstly the unsteady velocity profiles concur with each other for t<0.4 whereas subsequently, they diverge for t≥0.4. Furthermore, the overshoot of the U curves is elevated as β is increased. The reason behind this augmentation is that cumulative β values decrease the magnitude of the viscous shear diffusion terms in Eq. (8) which manifests in a reduction in resistance “to the fluid flow in the region of the temporal maximum of velocity”. Also, for each Da values with β=1, Figure 3(b) depicts that it has equivalent transient nature as the deviation of velocity profile pertaining to β as shown in Figure 3(a). As explained in Figure 3(a), it is seen that initially, unsteady U profiles merge together for t<1 and then diverge for t≥1. Also, the overshoot of the U curve increases as Da is enhanced, since greater Darcy number corresponds to higher permeability of the porous medium and an associated depletion in bulk matrix drag of the porous medium fibers. The flow is therefore accelerated with higher Darcy number. Also, it is evident from Figures 3(a) and (b) that when parameters β or Da increase, the time taken to achieve temporal peak decreases for the velocity. Further, from Figure 3(a), it is observed that the time to attain the steady-state increases when β increases and the converse response is computed for increasing Da in Figure 3(b). These observations are confirmed in Table 3. The steady-state velocity (U) drawn in Figure 4 along “R coordinate at X=1.0” for distinct values of β and Da. Figure 4(a) shows the “unsteady U profile” for various values of β with Da=5 and Figure 4(b) for variation of Da with β=1 (note that the Newtonian case is retrieved only for infinite β values). Apparently, the velocity graph “starts with zero value at surface of cylinder”, attains the peak value and subsequently reduces to zero in the R direction. From Figure 4(a), it is seen that neighboring to the heated cylindrical wall (i.e., in the province 1 Figure 3 Time-dependent velocity profile (U) versus time (t) at point (1, 2.02) for effect of b (a) and Da (b) Figure 4 Simulated time-independent state velocity profile (U) versus R at X=1.0 for effect of b (a) and Da (b) The time-dependent temperature (θ) profiles at the spatial coordinate (1, 1.53) are illustrated in Figure 5. Figure 5(a) depicts the influence of β with Da=5 and Figure 5(b) for the effect of Da with β=1. From Figure 5(a), it is remarked that for various β values, the unsteady θ curves at first coincide together and then diverge after some interval of time. Further, it is perceived that the maximum value of temperature reduces as the Casson fluid parameter increases implying that greater viscoplastic effect serves to cool the regime and to decrease thickness of the thermal boundary layer. Figure 5(b) illustrates that for all values of Da with β=1, the same transient features are computed in temperature distributions as encountered earlier in Figure 5(a) with Da fixed and β varied. Also, it is remarked that as the Da rises the temperature decreases. The decrease in presence of “solid fibers in the porous medium” with higher permeability (i.e., larger Da) results in a diminished thermal conduction effect. This cools the regime and lowers temperatures also decreasing thermal boundary layer thickness. Also, from Figures 5(a) and (b) it is seen that the time required for achieving the temporal maximum decreases as Da or β increases. The simulated graph of time-independent θ profiles for distinct β values and Da against the R are revealed in Figure 6. Figure 6(a) shows the effect of Casson fluid parameter (β) with Da=5 and Figure 6(b) for Da with β=1. These figures indicate that the temperature (θ) curves commence with a wall temperature and then decay progressively to the free stream zero value along the radial axis R. Also, from Figure 6(a) it is remarked that the time-independent state temperature (θ) profile decreases with Casson viscoplastic effect, i.e., with greater β values. The thicker temperature profiles occur due to larger β and since a larger β induces deceleration in the flow which aids thermal diffusion. Also, the time required to accomplish the steady-state rises as β rises. Figure 6(b) depicts that the steady-state temperature value is diminished with greater Da. Also, the time taken to attain the time-independent state decreases as Da increases. 4.2 Friction and heat transport coefficients The non-dimensional average skin-friction Figure 5 Simulated time-dependent temperature profile (θ) versus time (t) at point (1, 1.53) for effect of β (a) and Da (b) Figure 6 Time-independent state temperature profile (θ) versus R at X=1.0 for effect of β (a) and Da (b) The The variations β and Da values on Nusselt number ( Figure 7 Average momentum transport coefficient Figure 8 Average heat transport coefficient 4.3 Entropy heat generation analysis and Bejan number The entropy generation per unit volume for incompressible Casson fluid is given as [35–37] Eq. (14) can be rewritten as The individual terms are defined by Above entropy generation expression (16) contains S1, S2 and S3 which represent the irreversibility owing to conductivity (k), viscosity (μ) and porous medium (μ/k1) effects, respectively. The non-dimensional form of Sgen is represented as entropy heat generation parameter Ns which is defined ratio of actual entropy heat generation rate to the characteristic entropy heat generation rate. Therefore, parameter Ns can be written as [38] where where To measure the irreversibility distribution, the parameter Be (Bejan number) represents the ratio of entropy heat generation due to heat transfer to the overall entropy heat production, and is given by Ref. [39]. The impact of the key thermophysical and rheological flow parameters on entropy generation (Ns) against t at the position (1, 2.40) is depicted in Figure 9. The impact of non-dimensional Casson fluid parameter (β), Darcy parameter (Da), group parameter (ε1Θ–1) and Grashof number (Gr) on unsteady Ns profiles are shown in Figures 9(a)–(d), respectively. From all these graphs, it is seen that, in the beginning, the Ns curves upsurge drastically, then decline, then again ascend, attain a temporal maximum, and lastly turn out to be steady-state. This unsteady behavior of Ns is noticed at another location also. In the initial stage, the time- dependent nature of the entropy profiles is more dramatic. From Figure 9(a), it is seen that for various β values, the steady-state entropy profiles which initially concur with each other subsequently split after a certain time. Also, a critical look from Figure 9(a), is that the Ns upturns with augmenting β. Also, in Figure 9(b), it may be deduced that as Da increases the transient Ns reduces strongly and becomes weak in the interval Figure 9 Transient entropy generation number (Ns) against time (t) at point (1, 2.40) for different values: The computer-generated time-independent entropy (Ns) profiles for different hydrodynamic and thermal control parameters β, Da, Gr and ε1Θ–1 along the R coordinate at X=1.0 are presented in Figures 10(a)–(d), respectively. The Ns magnitudes substantially increase quickly arriving at the peak value as the radial position augments. Following this there is a sharp descent and then a gradual monotonic decay to zero. Ns profiles are sharpened edge at the peak value in the environs of the hot cylindrical surface. On the other hand, the velocity curves are smoother at the peak value as revealed in Figures 4(a) and (b). The entropy production results in a thinner R boundary layer for all control parameter values, which is attributable to higher entropy production nearby the hot wall. Figure 10(a) signifies the effect of β on Ns. As viscoplastic Casson parameter β, is increased, there is a strong enhancement in steady-state Ns values in close proximity to the cylinder wall (i.e., in the interval Figure 10 Steady-state entropy generation number (Ns) against R at X=1.0 for different values: Figures 11(a)–(d) are plotted to explain the evolution of Bejan number (Be) with time (t) at the location (1, 2.40) for selected ranges of the parameters β, Da, Gr and ε1Θ–1, respectively. These figures imply that Be commences initially with zero value, increases radically and achieves the maximum value, then falls marginally, and finally turn out to be asymptotically steady after a slight oscillation. From Figure 11(a), it is observed that, in the initial stages of flow, the irreversibility caused by “heat transfer controls the entropy” and when t>0.45 the “fluid friction” dominates. In Figures 11(a)–(b), it is noticed that for all β and Da values Bejan number drastically increases in the interval Figure 11 Transient Bejan number (Be) against time (t) at location (1, 2.40) for different values: Finally, Figures 12(a)–(d) illustrate the distribution of time-independent state Bejan number, Be versus radial coordinate at X=1.0 for variation in β, Da, Gr and ε1Θ–1, respectively. Invariably the steady-state features of Be are analogous to the time-independent state Ns described earlier in Figures 10(a)–(d). From Figure 12(a), as β rises, it is viewed that the steady-state Be increases in the interval Figures 13(a)–(b) present the entropy lines distinct values of β, Da, ε1Θ–1 and Gr. In Figure 13(a), the effect of β is shown in the sub Figures 13(a1) and (a2); and the effect of Da is shown in Figure 13(a2) and (a3). Similarly, the variation of control parameters ε1Θ–1 & Gr is shown in Figure 13(b). From Figures 13(a1), (a2), (a3), it is revealed that the entropy lines becoming close to the hot wall as β or Da increases. Likewise, in Figures 13(b1) and (b2), the entropy lines are observed to move away from the hot wall as ε1Θ–1 increases. However, in Figures 13(b2) and (b3), there is no substantial variation in entropy lines as the flow takes place from the hot wall to the cold wall with increasing values of Gr. The significant remark from these figures is the entropy production take place only in the vicinity of the hot cylindrical wall for all values of β, Da, Gr and ε1Θ–1. Figure 12 Steady-state Bejan number (Be) against R at X=1.0 for different values: Figure 13 Simulated steady-state entropy lines (Ns) in 2D coordinate system (X, R) for various values: In a similar way, the Bejan lines for various values of thermophysical parameters are visualized in Figures 14(a) and (b). For all values of β, Da, Gr and ε1Θ–1, it is identified that the variation of Bejan lines is confined to the vicinity of the hot cylindrical surface only. From Figure 14(a), it is clear that the Bejan lines approach closer to the hot wall with increasing values of β whereas they depart further from the all with increasing Da. Figure 14(a) also indicates that the Be curves fluctuate in the rectangular region, i.e., 0≤X≤1, 2≤R≤3. This fluctuation is more significant for Da as compared to β. However, in Figure 14(b), this type of fluctuation is absent for Be curves when Grashof number, Gr or ε1Θ–1 increase. Finally, in Figure 14(b) it is apparent that the Bejan lines back off from the hot wall as ε1Θ–1 or Gr increases. 4.4 Stream and heat functions The fluid motion is presented by means of the dimensionless stream function ψ which is obtained from velocity constituents U and V and which satisfies the mass conservation (continuity) Eq. (7). The correlation between U, V, and ψ for 2-D incompressible flows is given by On simplification, this equation yields Likewise, the “heat function Ω′ for the temperature” is defined as Clearly, Ω′ satisfies the energy Eq. (4). The dimensionless heat function, Equations (22a) and (22b) in terms of Ω can be re-written as Clearly above Eqs. 23(a) and 23(b) satisfy the steady-state version of energy equation Eq. (9) identically and using Eqs. (23a, b), Poisson equation is constructed for the heat function. Figures 15(a)–(c) describe the streamlines, isotherms and heat lines graphs for different values of β and Da, respectively. The dimensionless values of ψ, θ and Ω, are evaluated by central differences formulae of second-order. In each graph the effect of β is revealed in Figures 15(a1, b1, c1) and (a2, b2, c2); also, Da shown in Figures 15(a2, b2, c2) and (a3, b3, c3); and again Figures 15(a3, b3, c3) and 15(a4, b4, c4) for Casson and Newtonian fluid (β=∞) flows, respectively. The heat lines and isotherms appear nearby by the hot cylindrical wall in comparison to the streamlines. From Figures 15(a1) and (a2), it is seen that as Casson viscoplastic parameter, β, increases, the streamlines tend to gravitate closer to the hot wall. Figure 15(a2) and (a3) shows that the streamlines depart away from the cylindrical surface as Da increases. Also, it is viewed that as Da upsurges, the streamlines pattern is transformed strongly. Similarly, from Figure 15(a3) and (a4), the streamlines are closer for the Newtonian fluid as compared to the Casson fluid. The streamlines are thicker around the leading edge of the cylinder as observed in Figure 15(a1)–(a4). From Figure 15(b1)–(b4), it is evident that isotherms wall as Da or β, augments. Also, as β, or Da are increased, the variation in isotherms is minimized. Further, the drawback of streamlines and isotherms can be overcome by using heat lines which is explained in Refs. [31, 40]. Figure 14 Simulated steady-state Bejan lines (Be) in 2D coordinate system (X, R) for various values of β, Da (a) and ε1Θ–1, Gr (b) Figure 15 Time-independent state: The heat lines specify surrounded passageways and are a useful tool for visualization of heat transfer and analysis, providing much more information than isotherms. Heat lines are found to migrate slightly towards the cylindrical surface as Da increases and the opposite trend is computed with increasing seen β. Also, as β, or Da increases, the extreme value of Ω increases, since 4.5 Casson and Newtonian fluid flows comparison Tables 3 and 4 document the temporal maximum and the steady-state values for the flow- field variables between Casson and Newtonian fluid flows for Da, β, Gr and ε1Θ–1. Table 3 signifies Casson fluid and Table 4 corresponds to a Newtonian fluid. With increasing Da and β, the time taken for U and θ variables to reach the temporal peak for the Casson fluid is more than the Newtonian fluid and the converse trend is observed for Ns and Be. Similarly, for every Da and β, the steady-state time for U, θ, Ns and Be is greater for Newtonian fluid as compared to that of Casson fluid. Also, for each Da and β, the maximum velocity values occur at X=1.0, and these values for “Casson fluid” are smaller compared with those of “Newtonian fluid”. Table 3 Time required for various variables to attain temporal peak and time-independent state, peak velocity for various β, Da, Gr and ε1Θ–1 with Pr=0.71 for Casson fluid Table 4 Time required for various variables to attain temporal peak and time-independent state, peak velocity for various β, Da, Gr and ε1Θ–1 with Pr=0.71 for Newtonian fluid Table 5 presents the variances between the “Casson fluid” and “Newtonian fluid” for average skin-friction and Nusselt number with various Da and β. From Table 5, it is perceived that the values of the wall shear stress of a “Casson fluid” are superior compared to the “Newtonian fluid”. However, the reverse trend is noted for the average Nusselt number. Thus, the features of average wall shear stress and heat transfer rate of “Casson fluid” considerably vary from that of the “Newtonian fluid”. Computational domain (X, R) except at the boundary points (X=0, R=1 & R=20), the flow of “Casson fluid” velocity is seeming to be smaller than for a “Newtonian fluid”. However, for the temperature profiles, the trend is reversed. Also, the “time-independent state” velocity and temperature contours for a “Casson fluid” are somewhat different with thicker hydrodynamic and thermal boundary layers than those of a “Newtonian fluid”. Figures 16(a) and (b) depict the Casson and Newtonian flow-field contours (U and θ) respectively. At any spatial coordinate location in the 2-dimensional rectangular computational domain (X, R) except at the boundary points (X=0, R=1 & R=20), the flow of “Casson fluid” velocity seems to be smaller than for a “Newtonian fluid”. However, for the temperature profiles, the trend is reversed. Also, the “time-independent state” velocity and temperature contours for a “Casson fluid” are somewhat different with thicker hydrodynamic and thermal boundary layers than those of a “Newtonian fluid”. Table 5 Comparison between Casson fluid and Newtonian fluid flows for various values of β and Da with respect to average values of 5 Concluding remarks The entropy generation minimization along with Bejan’s heatline visualization technique has been employed in this article to examine heat transfer optimization in time-dependent free convective Casson fluid boundary layer flow from an isothermal cylinder embedded in a porous medium using the Crank-Nicolson technique. The physical characteristics of heatlines are enormously useful in visualizing heat transfer in the rectangular domain. Also, in a given rectangular 2-D computational domain, the heatlines provide a powerful method for evaluating the heat transfer rate at all levels. Also, the entropy generation and Bejan numbers are derived and assessed using flow-field variables. The influences of Casson fluid parameter and Darcy parameter on flow-field profiles along with friction factor and heat transfer rate are discussed. Furthermore, the effect of Casson fluid parameter, Darcy number, group parameter and Grashof number upon entropy generation and Bejan numbers are analyzed. The pertinent deductions from the present study may be summarized as follows: Figure 16 Time-independent state contours of velocity (U) and temperature (θ) in 2D coordinate system (X, R) with fixed values of Pr=0.71 and Da=1.2 for Casson fluid (β=1.0) (a) and Newtonian fluid (β=∞)(b) 1) The time needed for achieving the steady-state rises as Casson viscoplastic fluid parameter increases and the contrary trend is computed with increasing Darcy number. 2) The velocity upsurges and temperature reduces with escalating values of Casson viscoplastic fluid parameter or Darcy number. Also averaged momentum transport coefficient (skin friction) is amplified with greater values of Darcy number whereas it is decreased with increasing Casson viscoplastic fluid parameter. Similarly, the averaged heat transport coefficient (Nusselt number) is observed to increase with increasing values of Casson viscoplastic fluid parameter or Darcy number. 3) Entropy heat generation parameter and Bejan number increase with increasing values of Casson viscoplastic fluid parameter, Darcy number, Grashof number or group parameter. 4) The time to reach the temporal peak for entropy generation decrease with increasing Casson viscoplastic fluid parameter or Darcy number, Grashof number or group parameter. 5) The time to accomplish the steady-state for the velocity, temperature, entropy generation and Bejan number increase with increasing viscoplastic fluid parameter, Darcy number or group parameter whereas they are reduced with increasing Grashof (free convection) number. 6) The transient and steady-state consequences of flow variables, friction factor and heat transfer rate, entropy production, Bejan number for non-Newtonian Casson fluid differ significantly from those computed for a Newtonian fluid. The present study has provided some interesting insights in entropy generation associated with non-Newtonian thermal convection boundary layer flows in porous media. Future studies will consider thermal stratification effects in porous media and alternative (e.g., Oldroyd-B viscoelastic) rheological models and also nanofluids and will be communicated imminently. Acknowledgements The third author MAHESH Kumar wishes to thank DST-INSPIRE (Code No. IF160028) for the grant of research fellowship and to Central University of Karnataka for providing the research facilities. The authors wish to express their gratitude to the reviewers who highlighted important areas for improvement in this article. Their suggestions have served to enhance the clarity and depth of the interpretation in particular. Nomenclature Be Dimensionless Bejan number Average momentum transport coefficient cp Specific heat g Gravity Da Darcy number Gr Grashof number k1 k1permeability parameter Ns Dimensionless entropy heat generation number k Thermal-conductivity of the fluid Nusselt number py Yield stress Pr Prandtl number r0 Radius of the cylinder r Radial coordinate R Dimensionless radial coordinate t′ Time t Dimensionless time T′ Temperature u, v Velocity components x Axial coordinate U, V Dimensionless velocity components X Dimensionless axial coordinate Greek letters θ Dimensionless temperature ε1 Dimensionless viscous dissipation parameter μ Viscosity of fluid α Thermal diffusivity Ω′ Heat function v Kinematic viscosity Ω Dimensionless heat function ρ Density ψ Dimensionless stream function βT Volumetric coefficient of thermal expansion ε1Θ–1 Dimensionless group parameter Θ Non-dimensional temperature difference Subscripts l, m Grid levels w Wall conditions ∞ Ambient conditions Superscript n Time step level References [1] SPARROW E M, GREGG J L. Laminar free convection heat transfer from the outer surface of a vertical circular cylinder [J]. ASME Journal of Heat Transfer, 1956, 78(8): 1823–1829. [2] LEE H R, CHEN T S, ARMALY B F. Natural convection along slender vertical cylinders with variable surface temperature [J]. ASME Journal of Heat Transfer, 1988, 110: 103–108. [3] MAKANDA G, SHAW S, SIBANDA P. Diffusion of chemically reactive species in Casson fluid flow over an unsteady stretching surface in porous medium in the presence of a magnetic field [J]. Mathematical Problems in Engineering, 2015: Article ID 724596. [4] DASH R K, MEHTA K N, JAYARAMAN G. Casson fluid flow in a pipe filled with a homogeneous porous medium [J]. International Journal of Engineering Science, 1996, 34: 1145–1156. [5] CASSON N. A flow equation for pigment oil suspensions of the printing ink type [M]// Rheology of Disperse Systems. Oxford: Pergamon Press, 1956: 84–102. [6] ABBAS Z, SHEIKH M, MOTSA S S. Numerical solution of binary chemical reaction on stagnation point flow of Casson fluid over a stretching/shrinking sheet with thermal radiation [J]. Energy, 2016, 95: 12–20. [7] MUSTAFA M, HAYAT T, POP I, HENDI A. Stagnation- point flow and heat transfer of a Casson fluid towards a stretching sheet [J]. Zeitschrift für Naturforschung A, 2012, 67: 70–76. [8] MYTHILI D, SIVARAJ R. Influence of higher order chemical reaction and non-uniform heat source/sink on Casson fluid flow over a vertical cone and flat plate [J]. Journal of Molecular Liquids, 2016, 216: 466–475. [9] DAS M, MAHATO R, NANDKEOLYAR R. Newtonian heating effect on unsteady hydromagnetic Casson fluid flow past a flat plate with heat and mass transfer [J]. Alexandria Engineering Journal, 2015, 54: 871–879. [10] NADEEM S, HAQ R U, LEE C. Magnetohydrodynamic flow of a Casson fluid over an exponentially shrinking sheet [J]. Scientia Iranica, 2012, 19: 1550–1553. [11] RAJU C S K, SANDEEP N, SUGUNAMMA V, BABU M J, REDDY J R. Heat and mass transfer in magnetohydrodynamic Casson fluid over an exponentially permeable stretching surface [J]. Engineering Science and Technology, 2016, 19: 45–52. [12] GIANGASPERO G, SCIUBBA E. Application of the entropy generation minimization method to a solar heat exchanger: A pseudo-optimization design process based on the analysis of the local entropy generation maps [J]. Energy, 2013, 58: 52–65. [13] BADESCU V. Optimal paths for minimizing lost available work during usual heat transfer processes [J]. Journal of Non-Equilibrium Thermodynamics, 2004, 29: 53–73. [14] KOCKUM H, JERNQVIST A. Entropy generation in multifield flows: Equations and Examples of Applications [J]. Chemical Engineering Research and Design, 1998, 76: 210–222. [15] BEJAN A. A study of entropy generation in fundamental convective heat transfer [J]. ASME Journal of Heat Transfer, 1979, 101: 718–725. [16] BEJAN A. Second law analysis in heat transfer [J]. Energy, 1980, 5: 720–732. [17] BEJAN A. Second law analysis in heat transfer and thermal design [J]. Advances in Heat Transfer, 1982, 15: 1–58. [18] MAHIAN O, OZTOP H, POP I, MAHMUD S, WONGWISES S. Entropy generation between two vertical cylinders in the presence of MHD flow subjected to constant wall temperature [J]. International Communications Heat and Mass Transfer, 2013, 44: 87–92. [19] MIRZAZADEH M, SHAFAEI A, RASHIDI F. Entropy analysis for non-linear viscoelastic fluid in concentric rotating cylinders [J]. International Journal of Thermal Science, 2008, 47: 1701–1711. [20] MAHIAN O, MAHMUD S, HERIS SZ. Analysis of entropy generation between co-rotating cylinders using nanofluid [J]. Energy, 2012, 44: 438–446. [21] BASSAM A K ABU-H, WALEED N H. Entropy generation due to laminar natural convection over a heated rotating cylinder [J]. International Journal of Heat and Mass Transfer, 1999, 42: 4225–4233. [22] JIA Q, MUHAMMAD M B, MUNAWWAR A A, MOHAMMAD M R, MOHAMED EL-S A. Entropy generation on MHD Casson nano fluid flow over a porous stretching/shrinking surface [J]. Entropy, 2016, 18(4): 1–14. [23] ASMA K, ILYAS K, ARSHAD K, SHARIDAN S. Unsteady MHD free convection flow of Casson fluid past over an oscillating vertical plate embedded in a porous medium [J]. Engineering Science and Technology, 2015, 18(3): 309–317. [24] RAMACHANDRA P V, SUBBA R A, ANWAR B O. Flow and heat transfer of Casson fluid from a horizontal circular cylinder with partial slip in non-Darcy porous medium [J]. Journal of Applied & Computational Mathematics, 2013, 2(2): 1–12. [25] HARI R, KATARIA, HARSHAD R P. Radiation and chemical reaction effects on MHD Casson fluid flow past an oscillating vertical plate embedded in porous medium [J]. Alexandria Engineering Journal, 2016, 55: 583–595. [26] KIMURA S, BEJAN A. The heatline visualization of convective heat transfer [J]. ASME Journal of Heat Transfer, 1983, 105: 916–919. [27] BEJAN A. Convection heat transfer [M]. New York: John Wiley and Sons, 1984. [28] RANI H P, REDDY G J. Heatline visualization for conjugate heat transfer of a couple stress fluid from a vertical slender hollow cylinder [J]. International Communications in Heat and Mass Transfer, 2013, 48: 46–52. [29] RANI H P, REDDY G J, KIM C N, RAMESHWAR Y. Transient couple stress fluid past a vertical cylinder with Bejan’s heat and mass flow visualization for steady state [J]. ASME Journal of Heat Transfer, 2015, 137: 032501. [30] MOREGA A. The heat function approach to the thermomagnetic convection of electroconductive melts [J]. Revue Roumaine des Sci Tech. Electrot et Energ, 1998, 33: 359–368. [31] MABOOD F, ABDEL-RAHMAN R G, LORENZINI G. Effect of melting heat transfer and thermal radiation on Casson fluid flow in porous medium over moving surface with magnetohydrodynamics [J]. Journal of Engineering Thermophysics, 2016, 25: 536–547. [32] RANI H P, JANARDHANA R G, KIM C N. Transient analysis of diffusive chemical reactive species for couple stress fluid flow over vertical cylinder [J]. Applied Mathematics and Mechanics ( English Edition), 2013, 34: 985–1000. [33] QING J, BHATTI M M, ABBAS M A, RASHIDI M M, ALI M EL-S. Entropy generation on MHD Casson nanofluid flow over a porous stretching/shrinking surface [J]. Entropy, 2016, 18: 1–24. [34] BUTT A S, ALI A, MEHMOOD A. Numerical investigation of magnetic field effects on entropy generation in viscous flow over a stretching cylinder embedded in a porous medium [J]. Energy, 2016, 99: 237–249. [35] MAHDAVI M, SAFFAR-AVVAL M, TIARI S, MANSOORI S. Entropy generation and heat transfer numerical analysis in pipes partially filled with porous medium [J]. International Journal of Heat and Mass Transfer, 2014, 79: 496–506. [36] BEJAN A. Entropy Generation Minimization [M]. New York, USA: CRC Press, 1996. [37] REDDY G J, KUMAR M, KETHIREDDY B, CHAMKHA A J. Colloidal study of unsteady magnetohydrodynamic couple stress fluid flow over an isothermal vertical flat plate with entropy heat generation [J]. Journal of Molecular Liquids, 2018, 252: 169–179. [38] REDDY G J, HIREMATH A, KUMAR M. Computational modeling of unsteady third-grade fluid flow over a vertical cylinder: A study of heat transfer visualization [J]. Results in Physics, 2018, 8: 671–682. [39] REDDY G J, KETHIREDDY B, KUMAR M, RANI H P, GORLA R S. Effect of Prandtl number for Casson fluid flow over a vertical cylinder: Heatline approach [J]. International Journal of Applied and Computational Mathe matics 2018, 4: 1–19. [40] SHEHZAD S A, HAYAT T, ALSAEDI A. Three-dimensional MHD flow of Casson fluid in porous medium with heat generation [J]. Journal of Applied Fluid Mechanics, 2016, 9: 215–223. (Edited by HE Yun-bin) 中文导读 多孔介质中垂直圆柱内Casson流体热对流的瞬态分析: 熵产和热能转移可视化 摘要:随着多孔介质在过滤系统、多孔轴承、多孔隔热层、生物力学、地质力学等方面的应用日益广泛,多孔介质中的热传输引起了工程科学领域的广泛兴趣。基于上述应用,本文就熵产对Casson黏塑性流体在多孔介质中均匀加热垂直圆柱上的分层不可压缩边界层流动中传热和动量传递的影响进行了数值研究。采用Darcy定律模拟了各向同性均质多孔介质在低Reynolds数时的体阻力效应,并进行热线可视化。利用适当的变换变量,推导了数学模型并进行归一化。利用隐式有限差分法求解了具有相关边界条件的非线性时变耦合控制方程,该方法有效且无条件稳定。结果表明,随着Darcy数、Casson流体参数、群参数和Grashof数的增大,熵产和Bejan数均增大。除了流线和等温线外,绘制热线为分析二维区域内的传热过程提供了一种很好的方法。结果表明,随着Darcy数的增加,热壁之间的传热线偏差减小。 关键词:垂直圆柱;熵产;Casson流体;有限差分法;热方程;多孔介质 Received date: 2017-12-17; Accepted date: 2018-10-23 Corresponding author: JANARDHANA REDDY G, PhD, Assistant Professor; Tel: +91-9491472461; E-mail: gjr@cuk.ac.in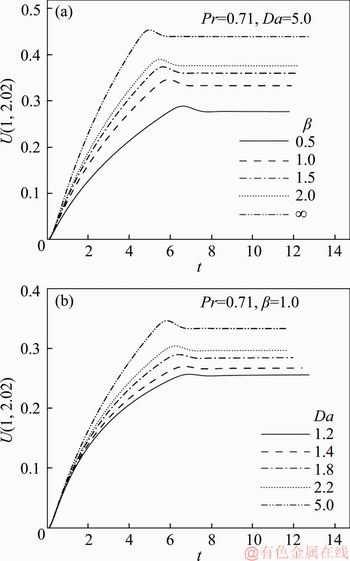

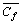 and heat transfer rate
and heat transfer rate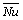 are given by
are given by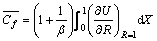 and
and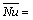
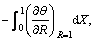 respectively.
respectively.
 graph for various β and Da are depicted in Figure 7. In Figures 7(a) and (b), it is seen that in the beginning for each value of β and Da, skin friction
graph for various β and Da are depicted in Figure 7. In Figures 7(a) and (b), it is seen that in the beginning for each value of β and Da, skin friction  upsurges with t, extents the maximum value, and then slightly diminishes, at the end it becomes asymptotically steady. This is logical since the free convective flow-field velocity is relatively small during the early transient period, as indicated in Figure 3, and the
upsurges with t, extents the maximum value, and then slightly diminishes, at the end it becomes asymptotically steady. This is logical since the free convective flow-field velocity is relatively small during the early transient period, as indicated in Figure 3, and the  remains less, as seen in Figure 7. Also, Figure 7(a) exhibits that
remains less, as seen in Figure 7. Also, Figure 7(a) exhibits that 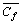 lessens for rising values of β and the reverse trend is seen for Da in Figure 7(b). It is apparent from Figures 7(a) and (b), that in the beginning time, the impact of the Casson viscoplastic parameter (β) on
lessens for rising values of β and the reverse trend is seen for Da in Figure 7(b). It is apparent from Figures 7(a) and (b), that in the beginning time, the impact of the Casson viscoplastic parameter (β) on 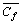 is more prominent than the Darcy parameter (Da). This is probably attributable to the augmented value of Casson fluid parameter (β) inducing an augment in the fluid viscosity which in turn retards the flow, i.e., decreases the U values in the boundary layer zone. Additionally, Figure 7 demonstrates that skin friction,
is more prominent than the Darcy parameter (Da). This is probably attributable to the augmented value of Casson fluid parameter (β) inducing an augment in the fluid viscosity which in turn retards the flow, i.e., decreases the U values in the boundary layer zone. Additionally, Figure 7 demonstrates that skin friction,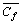 for the Casson fluid is more than Newtonian fluid.
for the Casson fluid is more than Newtonian fluid.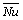 ) are depicted graphically in Figure 8, respectively. In these plots, it can be renowned that, for each β and Da value, initially the
) are depicted graphically in Figure 8, respectively. In these plots, it can be renowned that, for each β and Da value, initially the 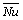 drastically reduces, then slightly upsurges and lastly achieves the steady-state. In the beginning time, the
drastically reduces, then slightly upsurges and lastly achieves the steady-state. In the beginning time, the 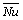 curves intersect each other for β and Da values and thereafter deviate once some time has elapsed. This indicates that in the initial period, heat conduction is the dominant heat transfer mode whereas with further time elapsing thermal conduction is subjugated by the thermal convection mode. Figures 8(a) and (b) determines that an augmenting in β or Da which implies to increasing values of the
curves intersect each other for β and Da values and thereafter deviate once some time has elapsed. This indicates that in the initial period, heat conduction is the dominant heat transfer mode whereas with further time elapsing thermal conduction is subjugated by the thermal convection mode. Figures 8(a) and (b) determines that an augmenting in β or Da which implies to increasing values of the 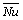 . It is apparent that escalating β values increase the spatial decay of the temperature flow-field in the vicinity of the hot wall due to flow deceleration near to the surface, which affects the escalation in heat transfer rate to the wall, i.e.,
. It is apparent that escalating β values increase the spatial decay of the temperature flow-field in the vicinity of the hot wall due to flow deceleration near to the surface, which affects the escalation in heat transfer rate to the wall, i.e., 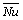 . Moreover, the heat transfer rate is swayed by the temperature gradient. In Figure 8(b), it is perceived that in the initial time level, i.e.,
. Moreover, the heat transfer rate is swayed by the temperature gradient. In Figure 8(b), it is perceived that in the initial time level, i.e., 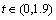
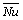 is almost the same for increasing values of Da (i.e., with higher k1), i.e., a variation in permeability does not markedly modify heat transfer rates at the wall. However, with further passage of time,
is almost the same for increasing values of Da (i.e., with higher k1), i.e., a variation in permeability does not markedly modify heat transfer rates at the wall. However, with further passage of time, 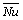 is significantly enhanced with increasing values of Da and attains the time-independent state. A further pertinent point of interest is that in Figure 8,
is significantly enhanced with increasing values of Da and attains the time-independent state. A further pertinent point of interest is that in Figure 8,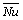 for a Casson fluid is substantially lower than that of the Newtonian fluid.
for a Casson fluid is substantially lower than that of the Newtonian fluid.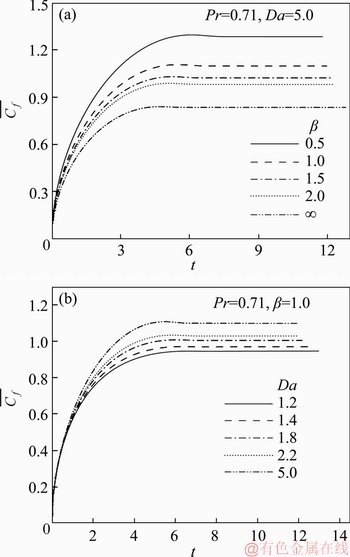
 profile against t for effect of β (a) and Da (b)
profile against t for effect of β (a) and Da (b)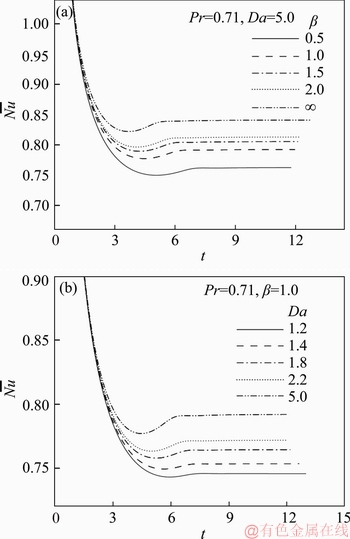
 profile against t for effect of β (a) and Da (b)
profile against t for effect of β (a) and Da (b)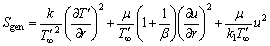 (14)
(14)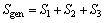 (15)
(15)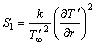 ,
,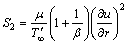 ,
,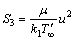 (16)
(16)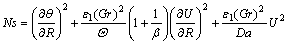 (17)
(17)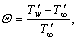 is the dimensionless temperature difference parameter, and
is the dimensionless temperature difference parameter, and 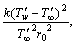 is the characteristic entropy heat generation. The Eq. (17) can be rephrased in the following form:
is the characteristic entropy heat generation. The Eq. (17) can be rephrased in the following form: (18)
(18) and
and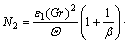
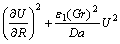 represents the irreversibility by heat transfer as a result of radial conduction and viscous dissipation to entropy generation respectively.
represents the irreversibility by heat transfer as a result of radial conduction and viscous dissipation to entropy generation respectively.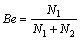 (19)
(19) and the converse trend is noticed for t>6.1. From Figures 9(a) and (b), it is comprehended that the time taken to attain temporal peak decreases as β or Da rises. In Figures 9(c) and (d), it is evident that, at first, the Ns curves rise radically, then reduces, next again upsurges, attains a temporal maximum, and at the end reaching the time-independent state. The significant remark noted here is that in the initial time phase all the Ns curves converge with each other and only deviate after some time for each control parameter values. The time required for achieving the temporal maxima decreases slightly as Gr or ε1Θ–1 increases. Thus, an elevation in Grashof number values (i.e., stronger thermal buoyancy force relative to viscous hydrodynamic force) results in increased entropy production.
and the converse trend is noticed for t>6.1. From Figures 9(a) and (b), it is comprehended that the time taken to attain temporal peak decreases as β or Da rises. In Figures 9(c) and (d), it is evident that, at first, the Ns curves rise radically, then reduces, next again upsurges, attains a temporal maximum, and at the end reaching the time-independent state. The significant remark noted here is that in the initial time phase all the Ns curves converge with each other and only deviate after some time for each control parameter values. The time required for achieving the temporal maxima decreases slightly as Gr or ε1Θ–1 increases. Thus, an elevation in Grashof number values (i.e., stronger thermal buoyancy force relative to viscous hydrodynamic force) results in increased entropy production.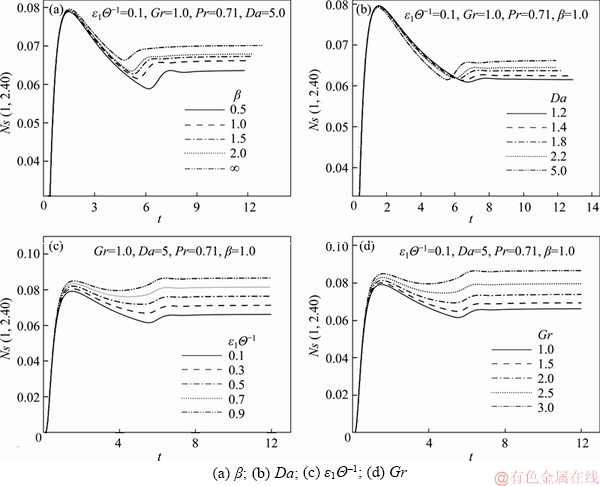
 ), and subsequently there is a depression in Ns magnitudes when R>3.5. The increase in the
), and subsequently there is a depression in Ns magnitudes when R>3.5. The increase in the  near to the cylinder surface results in an elevation in entropy generation, Ns (Figure 8(a)). From Figure 10(b), with increasing value of Da, the entropy profiles are boosted adjacent to the cylinder surface (i.e., in the region
near to the cylinder surface results in an elevation in entropy generation, Ns (Figure 8(a)). From Figure 10(b), with increasing value of Da, the entropy profiles are boosted adjacent to the cylinder surface (i.e., in the region  ), however, they are subsequently decreased when R>3. It is identified that as either Da or β is increased, the entropy profiles initially merge with each but later diverge with greater values of radial coordinate, R. Therefore, the variation of Da on Ns is of a similar nature to the impact computed with increasing Casson viscoplastic parameter, β. Figure 10(a) further indicates that the production of entropy nearby the hot wall (i.e., in the interval 1
), however, they are subsequently decreased when R>3. It is identified that as either Da or β is increased, the entropy profiles initially merge with each but later diverge with greater values of radial coordinate, R. Therefore, the variation of Da on Ns is of a similar nature to the impact computed with increasing Casson viscoplastic parameter, β. Figure 10(a) further indicates that the production of entropy nearby the hot wall (i.e., in the interval 1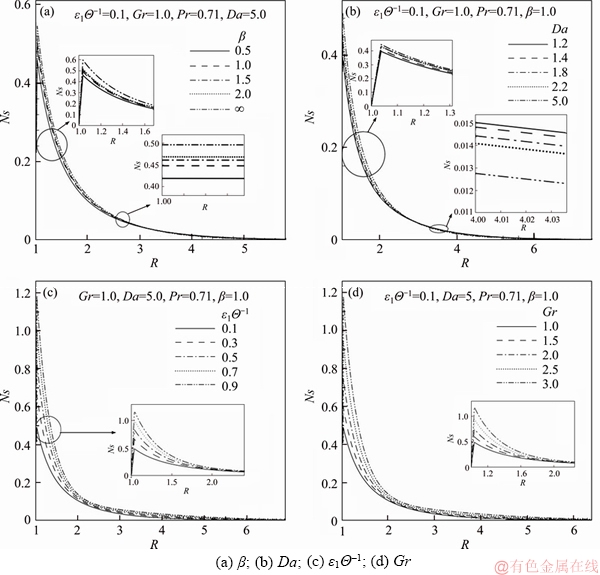
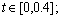 however when t>0.4, Be splits and reaches the temporal peak and thereafter attains the steady-state asymptotically. Also, as β increases, the Bejan number rises. From Figure 11(b), it is evident that increasing Da manifests in decreasing values in Be. Another remark in Figures 11(a) and (b) is that the time taken to reach the temporal peak decreases as β or Da increases. Figures 11(c) and (d) reveal that as Gr or ε1Θ–1 rises, there is a resultant elevation in Bejan number and additionally it is emphasized that the time elapse before a temporal-peak and the “time-independent” state is attained follows a similar behaviour to that computed as Gr or ε1Θ–1 are increased. Also, it is perceived that as Gr or ε1Θ–1 increases, Bejan number increases.
however when t>0.4, Be splits and reaches the temporal peak and thereafter attains the steady-state asymptotically. Also, as β increases, the Bejan number rises. From Figure 11(b), it is evident that increasing Da manifests in decreasing values in Be. Another remark in Figures 11(a) and (b) is that the time taken to reach the temporal peak decreases as β or Da increases. Figures 11(c) and (d) reveal that as Gr or ε1Θ–1 rises, there is a resultant elevation in Bejan number and additionally it is emphasized that the time elapse before a temporal-peak and the “time-independent” state is attained follows a similar behaviour to that computed as Gr or ε1Θ–1 are increased. Also, it is perceived that as Gr or ε1Θ–1 increases, Bejan number increases.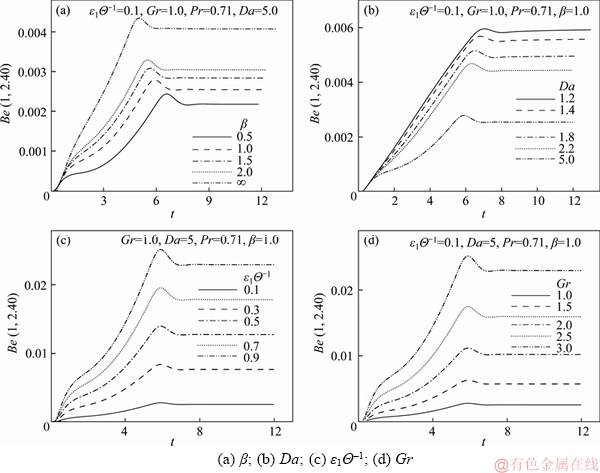
 , then decreases in the interval
, then decreases in the interval  and again increases in the interval
and again increases in the interval 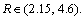 Similarly in Figure 12(b), the same tendency is attained for augmenting values of Da. Figures 12(c) and (d) reveal that, in the neighbourhood of the hot cylindrical wall, the Bejan number escalates rapidly, then shrinkage drastically, and eventually approaches a vanishing value at high values of the radial coordinate. With increasing values of Gr or ε1Θ–1, Bejan numbers are clearly enhanced. A noteworthy feature of both Figures 10 and 12 is that the time-independent state entropy production exceeds the Bejan number nearby the wall. This endorses that less Be yields an escalation in N2, i.e., N1
Similarly in Figure 12(b), the same tendency is attained for augmenting values of Da. Figures 12(c) and (d) reveal that, in the neighbourhood of the hot cylindrical wall, the Bejan number escalates rapidly, then shrinkage drastically, and eventually approaches a vanishing value at high values of the radial coordinate. With increasing values of Gr or ε1Θ–1, Bejan numbers are clearly enhanced. A noteworthy feature of both Figures 10 and 12 is that the time-independent state entropy production exceeds the Bejan number nearby the wall. This endorses that less Be yields an escalation in N2, i.e., N1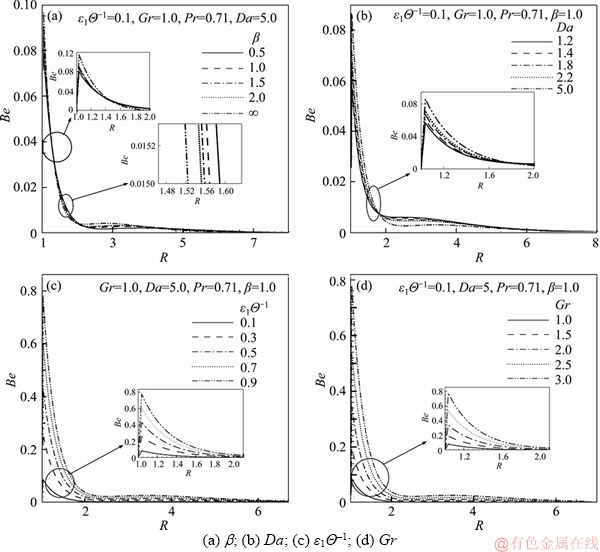
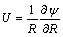 and
and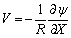 (20)
(20)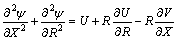 (21)
(21)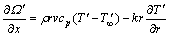 (22a)
(22a)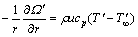 (22b)
(22b)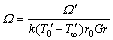 portray the heat function non-dimensional. It is well-known that the maximum value of this function conforming the overall
portray the heat function non-dimensional. It is well-known that the maximum value of this function conforming the overall 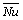 value on the hot wall [26].
value on the hot wall [26].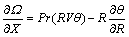 (23a)
(23a)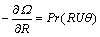 (23b)
(23b)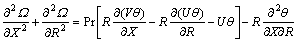 (24)
(24)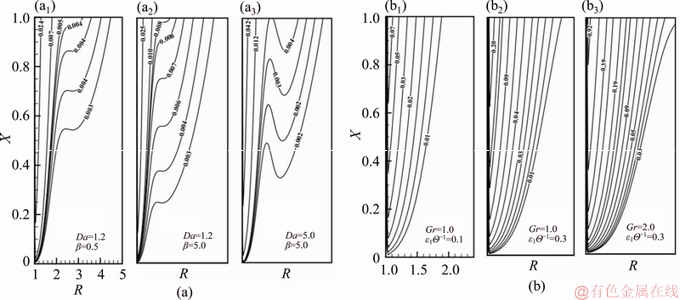
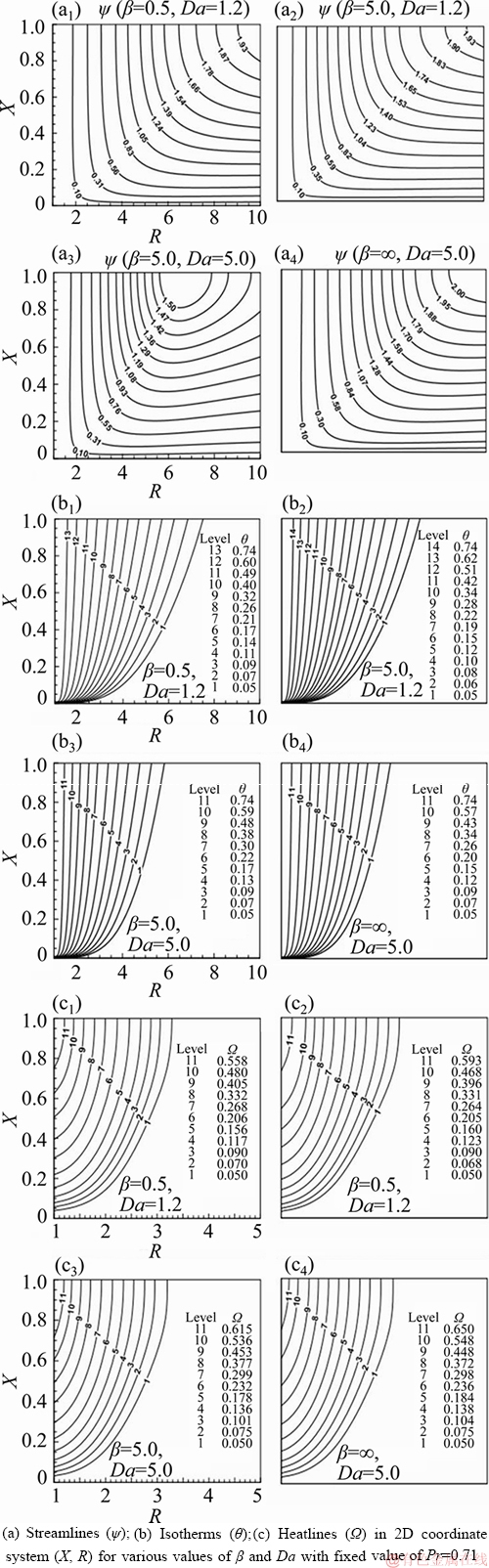
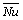 upsurges on the hot wall as presented in Table 4. The heat function Ω values for the Newtonian fluid exceed those for the Casson fluid. Furthermore, the deviation of heat lines from the hot cylindrical wall for a Newtonian fluid (β=∞) is less pronounced than that computed for the Casson fluid. Lastly, it is remarked that the heatlines variation is intensified in the proximity of the hot cylindrical wall in contrast to the streamlines and isotherms.
upsurges on the hot wall as presented in Table 4. The heat function Ω values for the Newtonian fluid exceed those for the Casson fluid. Furthermore, the deviation of heat lines from the hot cylindrical wall for a Newtonian fluid (β=∞) is less pronounced than that computed for the Casson fluid. Lastly, it is remarked that the heatlines variation is intensified in the proximity of the hot cylindrical wall in contrast to the streamlines and isotherms.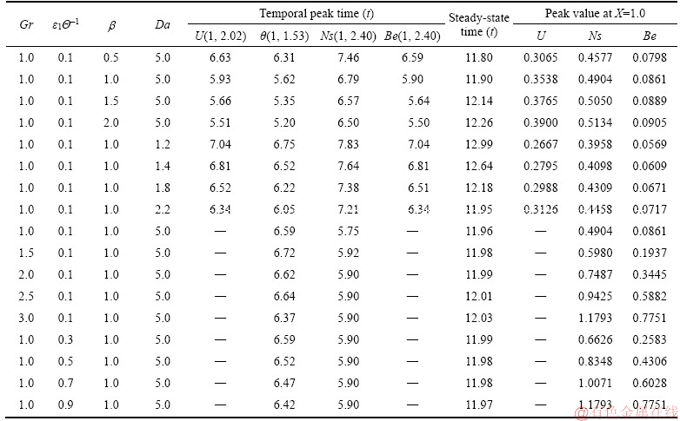
 and
and  with Pr=0.71
with Pr=0.71