Relaxations and bonding mechanism of arsenic in-situ impurities in MCT: first-principles study

 Sun Li-zhong(孙立忠)^{1, 2}, Zhong Xiang-li(钟向丽)¹, Wang Jin-bin(王金斌)¹,

Chen Xiao-shuang(陈效双)², Lu Wei(陆 卫)²

1. Key Laboratory of Advanced Materials and Rheological Properties of Ministry of Education,

Faculty of Materials and Optoelectronic Physics, Xiangtan University, Xiangtan 411105, China;

2. National Laboratory for Infrared Physics, Shanghai Institute of Technical Physics,

Chinese Academy of Sciences, Shanghai 200083, China

Received 1 March 2006; accepted 30 May, 2006

Abstract: The structural and electronic properties of the arsenic in-situ impurity in Hg_1-xCd_xTe(MCT) were studied by combining the full-potential linear augmented plane wave (FP-LAPW) and plane-wave pseudopotential methods base on the density functional theory. Structural relaxations, local charge density, densities of states are computed to investigate the effects of the impurity on the electronic structure. The bonding characteristics between the impurity and the host atoms are discussed by analysis of the valence charge density and the bonding charge density. The amphoteric behavior of arsenic impurity in MCT has been shown. The defect levels introduced by the in-situ arsenic impurities are determined by the single-particle electron energy calculations, which are in good agreement with the experimental results.

Key words: Hg_1-xCd_xTe; arsenic impurity; atom relaxation; bonding mechanism; first-principle study

1 Introduction

Mercury cadmium telluride (Hg_1-xCd_xTe, MCT) is currently one of the most widely used semiconductor materials for infrared detector arrays. It is well known that the applications of the semiconductor materials, especially for Ⅱ-Ⅵ compounds and alloys, mainly depend on whether they can be doped with donor or acceptor[1]. For infrared detectors fabricated by Hg_1-xCd_xTe, the p on n heterojunction is currently the preferred device design. In recent years, due to its low diffusivity in Hg_1-xCd_xTe[2] compared with the native acceptor and the group Ⅰ elements, attention has been focused on group Ⅴ elements, especially arsenic, as the p-type dopant in heterojunction devices where a sharp doping profile is essential for device performance [3]. The experimental results indicat that arsenic can provide a shallow acceptor level in molecular beam epitaxy(MBE) Hg_1-xCd_xTe[4]. But the arsenic doping is strongly self-compensated, requiring annealing for its p-type electric activation[5]. At the same time, the amphoteric behavior of arsenic in Hg_1-xCd_xTe has been found in materials grown by bulk method[6], liquid phase epitaxy (LPE)[7], MBE[8], and MOCVD[9], with incorporation as a p-type dopant under Hg-rich conditions, and as an n-type dopant or un-active dopant under Te-rich conditions. Although MBE is done at much lower temperatures than LPE, and thus offers some distinct advantages, the group Ⅴ impurities are still observed to incorporate as donors[4], self-compensating the p-type doping. HARMAN ponted out that there is a significant fraction of the arsenic residing on the cation sub-lattice even under cation-saturated conditions. According to the arsenic dopant incorporation model[11] and the quasichemical predictions[12], some of  the doped arsenics in MCT grown by MBE are incorporated on the cation sublattice as isolated defects, As_Hg, unbound to vacancies, as donors. Although the arsenic incorporation can be switched from an n- to p-type through post-growth annealing, the electronic properties of in-situ As_Hg not only determine the material properties before annealing, but also mainly dominate the annealing activation process from n- to p-type. As we know that the the annealing process not only affect the electronic properties but also affect the structural properties [13,14] which is worth studying thoroughly. Moreover, for doping levels above 5×10¹⁸ cm^-3, the As activation efficiency drastically drops because of the As_Hg self-compensation[15,16]. Herein the complicated behavior of the arsenic impurities in MCT, we must study thoroughly the electronic properties of both As in-situ substitute Hg and As in-situ substitute Te in MCT. Although the models of the amphoteric behavior are suggested, there is not comprehensive consensus on the microscopic mechanism of group Ⅴ impurity incorpo- ration in MCT, which is essentially important for infrared focal plane array technology.

Some theoretical studies the arsenic doped MCT materials. However, the calculations reported with the ab initio method, to our knowledge, are lack. In our previous work[17], we have reported the relaxations, bonding mechanism and electronic structure of As_Hg in Hg_0.5Cd_0.5Te. In order to give full understanding of the electronic behaviors of the As in-situ impurities in MCT, we have performed the total energy calculations of full potential linear augmented plane wave (FP-LAPW) to systematically investigate the effect of the arsenic in-situ impurity on the electronic structure, the bonding mechanism with the host atoms, and the relaxation procedure in Hg_1-xCd_xTe. In this paper, we choose Hg_0.5Cd_0.5Te as the major prototype system. The reason why we choose such a mole fraction is that the computational results can be compared with that of the thoroughly studied Ⅱ-Ⅵsemiconductors (CdTe and HgTe) to some extent. On the other hand, the results can be easily extrapolated to other mole fraction composi- tions. Furthermore, the results and conclusions of the calculations on Hg_0.5Cd_0.5Te are confirmed, and also extended to the other mole fractions by using plane-wave pseudopotential calculations with larger supercells.

2 Computational procedure

The density functional theory (DFT) [18] calcula- tions are performed using the FP-LAPW method implemented in the WIEN2K package[19]. We adopt Perdew-Burke-Ernzerhof(PBE) functional[20] to describe the exchange-correlation interaction. We consider a 2×2×2 supercell(SC) with totally 64 atoms, consisting of eight quasi-zinc-blende crystal structure of unit cells Hg_0.5Cd_0.5Te (each unit cell contains eight atoms including 4 Te atoms, 2 Hg atoms, and 2 Cd atoms). In the SC model, one of the 16 mercury atoms or one of the 32 tellurium atoms, on the lattice site (0.5, 0.5, 0.5) of SC, is replaced by an arsenic atom. A  2×2×1 SC with 32 atoms of no impurity has been chosen as reference system for comparison purpose, and the computational parameters are set to be the same as the vacancy case. In order to ensure well convergence, the muffin-tin (MT) radius and the number of k-points for generating the final results have been carefully chosen after optimization. The states treated as valence are Hg(5d¹⁰6s²), Cd(4d¹⁰5s²), Te(5s²5p⁴), and As(4s²4p³). The muffin-tin radii are chosen to be 2.60 atomic unit (a.u.) for all the four kinds atoms. A satisfactory self-consistent convergence has been achieved by considering a number of FP-LAPW basis functions up to R_MTK_max=6.0 for the 64-atoms SC and R_MTK_max=7.0 for 32-atoms SC. The K_max is the maximum value of the planwave vector which determines the so called energy cutoff for the plane wave expansion. The self-consistent iteration is considered to be converged when both the total energy and the total charge in the atomic sphere are stable within 10^-4 eV per unit cell and 10^-4 electron charges per atom, respectively. The localized levels are deduced from the calculations of the single-electron energy levels at Γ point and are aligned using the energy levels of core electrons. The relaxation procedures are conducted following the damped Newton dynamic schemes. The criterion of the forces convergence for all atoms is set below 0. 5 eV/nm. The relativistic effect of spin-orbit(SO) coupling is also included.

To confirm the results on the supercell of 64 atoms using FP-LAPW calculations and extend the conclusions to the other mole fractions of MCT, the plane-wave pseudopotential code Vienna ab initio simulation package (VASP) is also used in this paper. In the VASP calculations, the core-electron interaction is modeled by the ultrasoft pseudopotentials, which can yield reasonably precise results with relatively low cutoff energy. Thus, it is possible to deal with the larger supercell. In the present paper, supercells with 256 and 512 atoms have been chosen. The plane-wave cutoff energy is chosen as 300 eV, the standard ultrasoft pseudopotentials from the VASP package are employed for all the cases, and the Brillouin zone is sampled by using 5×5×5 and 3×3×3 Monkhorst-Pack grid for 256-atoms and 512-atoms supercells, respectively. The energy convergent criterion is 1×10^-4 eV per unit cell, and forces on all relaxed atoms are less than 0.1 eV/nm

3 Results and discussion

3.1 Structural relaxation

The appearance of arsenic impurity in MCT induces the structural relaxation of the host and modifies the electronic structure of the system. Before relaxation of atomic structures, from the calculated total energy versus five different volumes around the lattice constants given by Vegard’s law, the equilibrium volumes have been obtained for MCT systems with and without impurities, respectively. All the calculated values are fitted to the Murnaghan equation of state. In comparison with the experimental results, the computed bond lengths of R(Te-Cd) and R(Te-Hg) are about 1% larger than that of the experimental results of CdTe and HgTe. Geometry optimizations reveal that the arsenic impurity, either substituted Hg or Te lead to inward relaxation of the NN atoms around the impurity, the calculated results of the radial relaxation of the NN atoms around the impurity are shown in Table 1.

Table 1 Radial relaxation results of nearest neighbor atoms around arsenic impurity(nm)

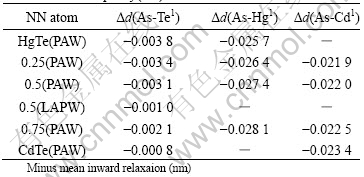
The relationship between the radial relaxation and mole fractions is also shown in Fig.1. The results indicate that the NN atoms around the impurity relax inward, either arsenic in-situ substitute Hg or Te. On the one hand, the inward radial relaxations due to the difference of the covalent radii between arsenic and host atoms, the covalent radii are 1.20, 1.36, 1.49, and 1.48 for As, Te, Hg, and Cd, respectively. On the other hand, the inward relaxation of the NN atoms around impurity is induced by the strong bonding mechanism between the arsenic and the host atoms, the detail will be discussed below. The relaxation also show that the As_Te impurity induce larger inward radial relaxations of the NN cations than that of the As_Hg. The results shown in Table 1 come from the calculations by using the PAW method with 64-atoms SC. In order to confirm the results of the FP-LAPW and PAW calculations on the supercell with 64 atoms, larger supercells have been used, such as supercells with 256 atoms and 512 atoms, respectively. The structural relaxations are conducted by using PAW method implemented in VASP. PAW calculations with 512-atoms supercells give the same relaxation trend of NN-atoms that of the 64 atoms SC calculations. The numerical results using two different methods both demonstrate the inward relaxations of NN-Te for x=0.5, as listed in Table 1. Larger radial relaxation of the PAW calculations comes from relatively small force criterion by comparison with that of FP-LAPW calculations. Considering the large calculated time consuming, full relaxation of atomic positions is used in PAW calculations, while symmetry constraint is applied in FP-LAPW calculations. Approximately linear relation- ship between the inward relaxation of the NN atoms and the mole fractions of MCT is shown in Fig.1. But, the linear relationship is inversed for As_Te and As_Hg doping case. Namely, the inward relaxations of the NN atoms become smaller as the mole fractions become larger for As_Hg, and become larger as the mole fractions larger for As_Te doping case.

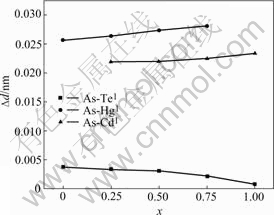
Fig.1 Relationship between inward radial relaxations of NN atoms and mole fraction of MCT

3.2 Bonding mechanism

In order to find out the reason of the NN atoms inward relaxation in MCT caused by arsenic impurity, the valence charge density and the bonding-charge density have been calculated. The bonding charge density is defined as the difference between the total charge density in the solid and the superpositions of neutral atomic charge densities placed at atomic sites, i.e.

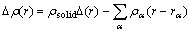              (1)

Therefore, the bonding-charge density represents the net charge redistribution as atoms are brought together to form the crystal. The bond re-hybridization induced by the arsenic impurity also can be revealed clearly by the bonding charge density. The calculated valence charge density and the bonding charge density of Hg_0.5Cd_0.5Te in the (110) plane, containing the arsenic impurity site are shown in the Figs.2 and 3. In which the dash lines mean the electrons move out relative to that of the atom superposition. From the Figs.2 and 3, we can see that the charge density distribution between the arsenic impurity and NN host atoms show the covalent characteristic either in the As_Hg or As_Te case. The valence charge density along the As-Te bond line in the case of As_Hg and As-Hg/Cd bond line in the case of As_Te have been picked up as shown in Figs.4 and 5. The figures indicate that As-Te bond and As-Hg/Cd bond are nearly perfect covalent bonds. Besides the smaller radius of arsenic than that of mercury and tellurium makes the NN tellurium inward relaxation, the stronger covalent bonding also results in NN host atoms inward relaxation. The bonding characteristics also give an explanation for the stably doping behavior of As in MCT.

Fig.2 Total charge density bonding charge density in (110) plane for As_Hg (Contour step size is 6×10^-3e/a.u.³ and 5×10^-3 e/a.u.³ for total charge density and bonding charge density, respectively.)

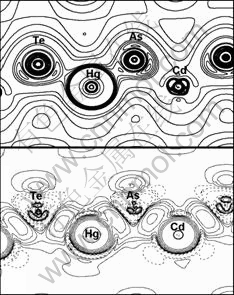
Fig.3 Total charge density bonding charge density in (110) plane for As_Te (Contour step size is 6×10^-3e/a.u.³ and 5×10^-3 e/a.u.³ for total charge density and bonding charge density, respectively.)

To obtain a measure of the hybridization strength

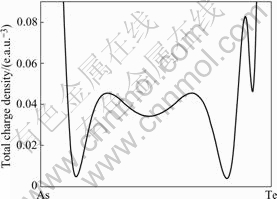
Fig.4 Total charge density along bond line of As-Te for case of As_Hg

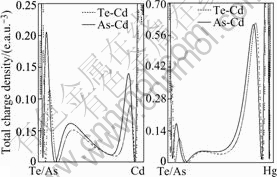
Fig.5 Total charge density along bond line of As-Hg/Cd for case of As_Te (Dash lines give charge density along Te-Hg/Cd bond line.)

between the orbital in the system, one can examine the density of states (DOS) and its partial density of states (p-DOS) which show how the “atomic” levels evolve into band states. The density of state(DOS) was calculated using the modified tetrahedron integration method and broadened using a Gaussian-like function with full width at half maximum (FWHM) equal to 0.1 eV. The total density of states (DOS) of un-doped and As_Hg- and As_Te-doped Hg_0.5Cd_0.5Te are shown in Fig.6. Substitution of a mercury and tellurium by a arsenic atom makes the resulting system metallic because of one arsenic p state electrons fill up to the conduction band for As_Te doping and want of one valence electrons relative tellurium for As_Te doping. The Fermi level does not lie within the band gap, but it extends to conduction band and valence band for As_Hg and As_Te, respectively, as shown in Fig.6. The density of states (DOS) integrated from CBM to the Fermi level accommodates one electron in As_Hg doped material. And in As_Hg doped material the integration from Fermi level to the mid of band gap also accommodates one electron. The results mean that the impurity As_Hg and As_Te in Hg_0.5Cd_0.5Te will behave as a single donor and a single acceptor, respectively. The theoretical predications agree well with the experimental results[7,8].

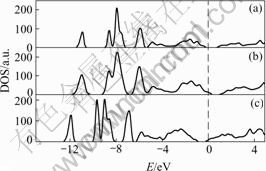
Fig.6 Total DOS of undoped-MCT-0.5(a), As_Te-MCT-0.5(b) and As_Hg-MCT-0.5(c) (Fermi level is set to zero)

For the case of charged neutral As_Hg, the defect center has total eleven electrons. Two of them occupy the a₁^V states, six of them occupy the t₂^V states and two of them occupy the a₁^C states which all locate in the valence band. The remaining one electron occupies the t₂^C which locates close to the conduction band as single donor. For the case of charged neutral As_Te, the defect center has total seven electrons. Two of them occupy the a₁^V states, five of them occupy the t₂^V states. One of unoccupied t₂^V state just above the VBM, behaves as single acceptor. The donor and acceptor levels for As_Hg and As_Te in MCT-0.5 determined by single-particle energy state are 19 meV above the VBM and 60 meV below the CBM which agree well with the experimental results[11].

4 Conclusions

The relaxations induced by the in-situ arsenic impurity have been given by combining FP-LAPW and PAW method. Both calculations give the same inward relaxation around the impurity. Through analysis of the charge density, nearly perfect covalent bond has been found between the impurity and host atoms. The bond characteristics between impurity and host atoms give the explanations for the stable doping behavior of arsenic in MCT. In the same time, the amphoteric behavior of arsenic impurity in MCT has been shown in the present paper.

The authors would like to thank Shanghai Super- computer Center for the computational supports.

[1] Neumark G F. Defects in wide band gap II-VI crystals [J]. Mater Sci Eng R, 1997, R21: 1-4.

[2] Berding M A, Sher A. Amphoteric behavior of arsenic in HgCdTe [J]. Appl Phys Lett, 1999, 74: 685-687.

[3] Sivananthan S, Wijewarnasuriya P S, Faurie J P. Recent progress in the doping of MBE HgCdTe [J]. Proc SPIE, 1995, 2554: 55-68.

[4] Shi x h, Rujirawat S, Ashokan R, Grein C H, Sivananthan S. Ionization energy of acceptors in as-doped HgCdTe grown by molecular beam epitaxy [J]. Appl Phys Lett, 1998, 73: 638-640.

[5] Garland J W, Grein C H, Yang B, Wijewarnasuriya P S, Aqariden F, Sivananthan S. Evidence that arsenic is incorporated as As4 molecules in the molecular beam epitaxial growth of Hg_1–xCd_xTe:As [J]. Appl Phys Lett, 1999, 74: 1975-1977.

[6] Vydyanath H R, Abbott R C, Nelson D A. Mode of incorporation of phosphorus in Hg_0.8Cd_0.2Te [J]. J Appl Phys, 1983, 54: 1323-1331.

[7] Vydyanath H R, Ellsworth J A, Devaney C M. Electrical activity, mode of incorporation and distribution coefficient of group V elements in Hg/sub 1-x/Cd/sub x/Te grown from tellurium rich liquid phase epitaxial growth solutions [J]. J Electron Mater, 1987, 16: 13-25.

[8] Sivananthan S, Wijewarnauriya P S, Awariden F, Vydyanath H R, Zandian M, Edwall D D, Arias J M. Mode of arsenic incorporation in HgCdTe grown by MBE [J]. J Electron Mater, 1997, 26: 621-624.

[9] Edwall B D, Chen J S, Bubulac L O. Arsenic doping in metalorganic chemical vapor deposition Hg_1–xCd_xTe using tertiarybutylarsine and diethylarsine [J]. J Vac Sci Tochnol B, 1991, 9: 1691-1694.

[10] Harman T C. Optically pumped LPE-growth Hg/sub 1-x/Cd/sub x/Te lasers [J]. J Electron Mater, 1989, 8: 191-200.

[11] Vydyanath H R. Amphoteric behaviour of group V dopants in (Hg, Cd)Te [J]. Semicond Sci Technol, 1990, 5: S213-S216.

[12] Berding M A, Sher A, Van Schilfgaarde m, Chen a c, Arias j. Modeling of arsenic activation in HgCdTe [J]. J Electron Mater, 1998, 27: 605-609.

[13] Zheng X J, Yang Z Y, Zhou Y C. Residual stresses in Pb(Zr_0.52Ti_0.48)O₃ thin films deposited by metal organic decomposition [J]. Scripta Mater, 2003, 49: 71-76.

[14] Zheng X J, Zhou Y C, Zhong H. Dependence of fracture toughness on annealing temperature in PZT thin films produced by metal organic decomposition [J]. Journal of Materials Research, 2003, 18(3): 578-584.

[15] Zandian m, Chen a c, Edwall d d, Pasko j g, Arias j m. p-type arsenic doping of Hg_1–xCd_xTe by molecular beam epitaxy [J]. Appl Phys Lett, 1997, 71: 2815-2817.

[16] Wijewarnasuriya p s, Sivananthan s. Arsenic incorporation in HgCdTe grown by molecular beam epitaxy [J]. Appl Phys Lett, 1998, 72: 1694-1696.

[17]SUN L Z, CHEN X S, SUN Y L, ZHOU X H, QUAN Z J, DUAN H, LU W. Structural and electronic properties of the in situ impurity AsHg in Hg_0.5Cd_0.5Te: first-principles study [J]. Phys Rev B, 2005, 71: 193203(1-4).

[18] Hohenberg p, Kohn w. Inhomogeneous electron gas [J]. Phys Rev, 1964, 136: B864-B971.

[19] Kohn w, Sham l j. Self-consistent equations including exchange and correlation effects [J]. Phys Rev, 1965, 140: A1133-A1138.

[20] Blaha p, Schwarz k, Madsen g, Kvasnicka d, Luitz j. 2001WIEN2k, An Augmented Plane Wave + Local Orbitals Program for Calculating Crystal Properties (Karlheinz Schwarz, Techn. University Wien, Austria).

(Edited by LONG Huai-zhong)

Corresponding author: SUN Li-zhong; Tel: +86-732-8292200; E-mail: lzsun@xtu.edu.cn