文章编号: 1004-0609(2006)06-0951-07

贵金属Cu、 Ag、 Au的电子结构和物理性质

陶辉锦, 谢佑卿, 彭红建, 余方新, 李晓波, 聂耀庄, 刘锐锋

(中南大学 材料科学与工程学院, 长沙 410083)

摘 要: 由纯金属单原子理论(OA)确定了面心立方结构(FCC)贵金属Cu、 Ag、 Au的电子结构依次为[Ar](3d_n)^5.58(3d_c)^4.21(4s_c)^0.23(4s_f)^0.98、 [Kr](4d_n)^4.87(4d_c)^4.56(5s_c)^0.66(5s_f)^0.91、[Xe](5d_n)^4.20(5d_c)^4.90 (6s_c)^1.57(6s_f)^0.33, 并确定了Cu、 Ag、 Au的密排六方结构(HCP)和体心立方结构(BCC)两种初态特征晶体和初态液体的电子结构。 根据自然态的电子结构定性解释了熔点、 拉伸强度、 维氏硬度、 体弹性模量、 电导和热导率物理性质差异与电子结构的关系, 定量计算了晶格常数、 结合能、 势能曲线及线热膨胀系数随温度的变化。 根据非自然态的电子结构, 定性解释了晶体结构BCC和HCP的关系。

关键词: Cu, Ag, Au; 电子结构; 晶体结构; 晶格常数; 结合能; 物理性质 中图分类号: TG111

文献标识码: A

Electronic structures and physical properties of Cu, Ag and Au

TAO Hui-jin, XIE You-qing, PENG Hong-jian, YU Fang-xin,

LI Xiao-bo, NIE Yao-zhuang, LIU Rui-feng

(School of Materials Science and Engineering,

Central South University, Changsha 410083, China)

Abstract: With the application of the One-Atom (OA) theory, the electronic structures of pure Cu, Ag and Au with FCC structure were determined, respectively. The electronic structures of these metals with HCP and BCC structure and LIQUID state were also determined. According to the electronic structure in natural state, the relationships between the differences of physical properties of Cu, Ag and Au and their electronic structures were explained qualitatively, and the lattice constants, cohesive energies, potential curves and the temperature dependence of linear thermal expansion coefficient of FCC-Cu, Ag and Au were calculated quantitatively as well. According to the electronic structure in unnatural state of HCP and BCC phases, the relationship between the electronic structure and crystalline structure was explained qualitatively.

Key words: Cu, Ag, Au; electronic structure; crystalline structure; lattice constant; cohesive energy; physical properties

金属材料系统科学框架^[1-5]包括3部分: 纯金属系统科学, 合金物理与化学和合金统计热力学。 建立这一框架的目的在与探索对金属与合金的电子结构与物理性质关系的全面描述。 这一框架以多原子相互作用势^{[6, 7]}, 晶格常数方程^[8], 原子状态杂化理论^{[9, 10]}和其它物理性质的理论作为基础, 对Ag-Cu^[11-14], Ti-Al^[15-17]和Au-Cu^[18-20]等合金系的原子状态, 原子势能, 原子动能, 原子体积, 体弹性模量和热膨胀系数等性质进行了系统研究。

在这一框架中, 核心内容是单原子(OA)理论。 基于这一理论, 运用自洽计算的方法可以计算纯金属的电子结构, 包括原子布居数、 原子价和化学键参数; 通过拟合计算的方法可以计算包括体弹性模量、 热膨胀系数和势能函数。 OA理论的目标在于建立纯单质数据库, 为复杂合金的设计、 制备及应用提供基本信息, 从而使材料设计在系统科学地指导下由经验设计步入科学设计阶段。 本文作者运用OA理论计算软件, 完成了纯金属Cu、 Ag和Au的电子结构和物理性质的计算, 并且分别和实验资料进行了对比和分析。

1 金属Cu、 Ag、 Au的基本原子态

在OA理论中, 纯金属的电子结构以若干基本原子态φ_k组成的单原子态ψa中准电子占有数(QEO)来描述:

在金属Cu、 Ag、 Au原子的外壳层中存在有共价电子n_c, 近自由电子n_f和非键电子n_n。 在每一基本原子态中, 电子分布服从Pauli不相容原理。

由Cu、 Ag、 Au各种基本原子态原子组成的赝晶体的特征性质(晶格常数a和结合能E_c)可由已建立的一系列公式^[3]求得。 表1所列为基本原子态及其相应的FCC结构赝晶体的特征性质。

2 自然态FCC-Cu、 Ag、 Au电子结构的确定

本研究中, 先以晶格常数a和结合能E_c这两个特征性质为依据, 在基本态组合系数步长为0.001的条件下对10个基本原子态选取三态进行杂化; 然后以晶格常数和结合能这两个物理量为主要依据确定对Cu、 Ag、 Au所取的三态组合成份为表2所列。

根据上表确定的电子结构分别为:

ψ(FCC-Cu)=[Ar](3d_n)^5.58(3d_c)^4.21(4s_c)^0.23(4s_f)^0.98

ψ(FCC-Ag)=[Kr](4d_n)^4.87(4d_c)^4.56(5s_c)^0.66(5s_f)^0.91

ψ(FCC-Au)=[Xe](5d_n)^4.20(5d_c)^4.90(6s_c)^1.57(6s_f)^0.33

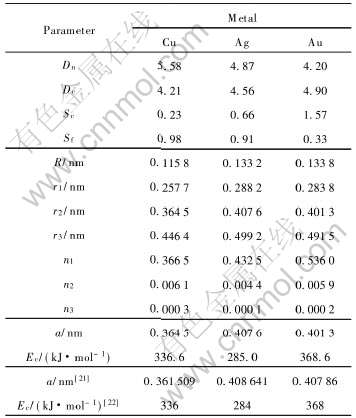
表3列出了FCC-Cu、 Ag、 Au晶体的原子状态参数、 键参数和特征性质, 其中r₁、 r₂、 r₃和n₁、 n₂、 n₃分别表示共价键键长(nm)和共价电子对数。

3 非自然态HCP-Cu、 Ag、 Au和BCC-Cu、 Ag、 Au初态特征晶体的电子结构

3.1 HCP-Cu、 Ag、 Au和BCC-Cu、 Ag、 Au的结合能

在等压条件下, 纯金属的Gibbs自由能为比热c_p(T)的函数:

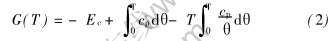
式中 H(0K)=-Ec。

在SGTE数据库中, Gibbs能用温度的幂级数形式表示为^[23]

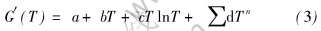
根据SGTE的晶格稳定参数^[24]得到的HCP和BCC结构的结合能分别为:

E_c(HCP-Cu)=335.4kJ/mol, E_c(BCC-Cu)=331.98kJ/mol; E_c(HCP-Ag)= 283.7kJ/mol; E_c(BCC-Ag)=280.6kJ/mol; E_c(HCP-Au)=367.76kJ/mol, E_c(BCC-Au)= 363.75kJ/mol.

表1 Cu, Ag和Au FCC赝晶体的基本原子态和特征性质

Table 1 Basic atom states and characteristic properties of pseudocrystals of Cu, Ag and Au

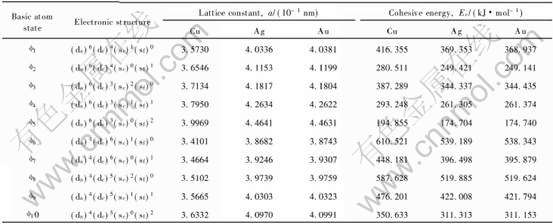
表2  FCC-Cu、 Ag和Au三态杂化成分表

Table 2 Hybridized concentration of three states of noble metal Cu, Ag and Au

表3 FCC-Cu、 Ag、 Au晶体的原子状态参数、键参数和特征性质

Table 3 Atom state parameters, bond parameters and characteristic properties of FCC-Cu, Ag and Au crystals

3.2 HCP-Cu、 Ag、 Au和BCC-Cu、 Ag、 Au的晶格常数

由于无法直接测定HCP-Cu、 Ag、 Au和BCC-Cu、 Ag、 Au的晶格常数, 故在本研究中采用对实验资料进行拟合外推的方法来求, 如对HCP结构选择Cu-Ge、 Cu-Sb、 Ag-Al、 Ag-Sb、 Au-In、 Au-Sn合金系中HCP固溶体相区的晶格常数进行多项式拟合, 并外推至端点求算术平均值求得HCP-Cu、 Ag、 Au的晶格常数和轴比分别为: a(HCP-Cu)=0.25533nm, c/a=1.669; a(HCP-Ag)=0.29386nm, c/a=1.660; a(HCP-Au)=0.2962nm, c/a=1.650, 同样选择Cu-Sn、 Cu-Zn、 Ag-Mg、 Ag-Zn、 Au-Cd、 Au-Zn合金系中BCC固溶体相区的晶格常数进行多项式拟合, 并外推至端点求算术平均值, 计算出BCC-Cu、 Ag、 Au的晶格常数分别为: 0.29066、 0.332和0.3187nm。

3.3 HCP-Cu、 Ag、 Au和BCC-Cu、 Ag、 Au的电子结构

与确定自然态FCC-Cu、 Ag、 Au的电子结构类似, 根据结合能和晶格常数由OA理论方可以确定HCP-Cu、 Ag、 Au的电子结构依次为: ψ(HCP-Cu)=[Ar](3d_n)^6.00(3d_c)^4.00 (4s_c)^0.32 (4s_f)^0.68, ψ(HCP-Ag)=[Kr](4d_n)^5.78(4d_c)^3.22(5s_c)^1.89(5s_f)^0.11, ψ(HCP-Au)=[Xe](5d_n)^6.00 (5d_c)^3.02 (6s_c)^1.83(6s_f)^0.15; BCC-Cu、 Ag、 Au的电子结构依次为: ψ(BCC-Cu)=[Ar](3d_n)5.26(3d_c)4.37 (4s_c)0.08 (4s_f)^1.29, ψ(BCC-Ag)=[Kr](4d_n)^5.75(34d_c)^3.29(5s_c)^1.84(5s_f)^0.13, ψ(BCC-Au)=[Xe](5d_n)^4.00(5d_c)^5.18 (6s_c)_1.20(6s_f)_0.62。

4 初态液体LIQUID-Cu、 Ag、 Au的电子结构

与HCP和BCC初态特征晶体的情况类似, 由SGTE数据库晶格稳定参数可求得初体LIQUID-Cu、 Ag、 Au的结合能依次为E_c(L-Cu)= 323.035kJ/mol, E_c(L-Ag)=272.975kJ/mol, E_c(L-Au)=355.448kJ/mol。

假定Cu、 Ag、 Au在熔化后仍具有FCC短程有序结构, 则根据其在熔化前后的密度^[25]及固态FCC-Cu、 Ag、 Au的晶格常数可推得液态L-Cu、 Ag、 Au的晶格常数依次为: a(L-Cu)=0.36675nm, a(L-Ag)=0.41441nm, a(L-Au)=0.41437nm。 与前面类似, 可以确定初体LIQUID-Cu、 Ag、 Au的电子结构依次为: ψ(L-Cu)=[Ar](3d_n)^4.35(3d_c)^4.65 (4s_f)^2.00, ψ(L-Ag)=[Kr](4d_n)^4.76(4d_c)^4.43 (5s_f)^1.81, ψ(L-Au)=[Xe](5d_n)^5.80(5d_c)^3.33 (6s_c)^1.76(6s_f)^0.10。

5 Cu、 Ag、 Au晶体结构演变的电子结构解释

p轨道电子云沿x、 y和z轴方向伸展, 轴向上的电子对核电菏的屏蔽作用最强, 而在轴间屏蔽较弱, 因此在轴间形成了两个弱屏蔽方向系统^[26]: 〈111〉方向的第一方向系统和〈110〉方向的第二方向系统, 前者是体对角线, 与px, py和pz轨道的夹角为54°44′, 后者是面对角线, 与px, py或pz轨道的夹角为45°。 原子核对第一方向系统上的电子吸引力最大, 对第二方向系统方向上的电子吸引力次之。

Cu、 Ag、 Au原子的p壳层已经充满, 而p⁶壳层外的d电子分裂为e_g和t_2g, 它们具有不同的能量和对称性。 e_g态d电子云沿〈111〉方向(即第一方向系统)伸展, 而t_2g态d电子云沿〈110〉方向(即第二方向系统)伸展。 d电子首先填充能量较低的e_g态轨道, 在〈111〉方向形成键瓣, 这些状态的原子聚合有利于形成对称性低的BCC结构的晶体^[14]。 同时, s电子云具有球对称性, 有利于形成高配位数结构的晶体。 本研究中电子结构的计算结果解释了Cu、 Ag、 Au贵金属BCC→HCP转变过程中晶体结构的成因, 即d_c电子减少(Cu: 4.37→4.00; Ag: 3.29→3.22; Au: 5.18→3.02), s_c电子增加(Cu: 0.08→0.32; Ag: 1.84→1.89; Au: 1.20→1.83), 使电子云分布的对称性增强而方向性减弱, 晶体结构向配位数增加的方向演变, 从而由BCC结构转化为HCP结构。

6 Cu、 Ag、 Au物理性质差异的电子结构解释

为了与实验结果进行比较, 这一部分的讨论只涉及自然态FCC结构Cu、 Ag、 Au。 金属的性质从本质上来说是金属晶体结合性质的体现。 可以认为, 总共价电子数n_c越多, 结合越强, 硬度和强度越大; 总自由电子n_f越多, 流动性越好, 塑性和延性越好, 因此可以以此二者作为判据来衡量金属力学性能的差异, 同时考虑体积因素, 可作如下参数定义: 共价电子浓度Tf=n_c/V和自由电子浓度Tr=n_f/V, V为原子体积。 根据凝聚态物理的固体电子论^[22], 电导率σ=ne²τ/m和热导率K=π²nk²BTτ/3m, 其中n为电子浓度, e为电子电量, τ为弛豫时间, m为电子质量, k_B为Boltzman_n常数, T为绝对温度。 若定性假定弛豫时间τ相等, 则在相同的温度T下, Cu、 Ag、 Au的电导率σ和热导率K只和电子浓度有关。

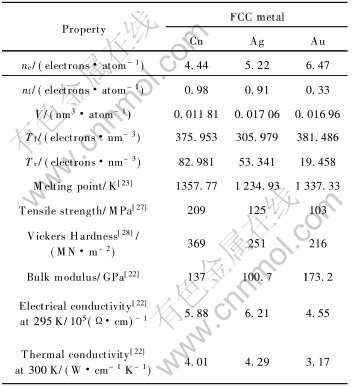
表4列出了FCC结构Cu、 Ag、 Au的电子浓度参数和各种性质, 熔点虽然一般不被当做力学性质, 但它可以作为一个衡量金属晶体结合强度的物理量, 又因为它可以被精确地测定, 且结果的分散度很小, 所以我们把熔点值也列入表3中。 结果表明: Cu、 Ag和Au的熔点、 体弹性模量、 电导率和热导率与T_f变化一致, 即共价电子浓度越大, 电子局域化程度越高, 流动性越差, 使得原子结合能越大, 抗压能力越强, 电导率和热导率越低; 另外一个方面, Cu, Ag和Au的抗拉强度和维氏硬度与T_r变化一致, 即, 自由电子浓度越大, 材料塑性和拉伸强度越好, 虽然硬度同时受到T_f与T_r的影响, 但是对于Cu、 Ag和Au, 其维氏硬度主要受到T_r的影响, 因而呈现与拉伸强度相似的规律。

表4 FCC结构Cu、 Ag、 Au物理性质差异与电子结构的关系

Table 4 Relationship between differences of physical properties of FCC-Cu, Ag and Au and their electronic structures

7 自然态FCC-Cu、 Ag、 Au物理性质的定量计算

以上部分对贵金属Cu、 Ag、 Au的电子结构与晶体结构和物理性质的关系进行了定性解释, 本节将对自然态FCC-Cu、 Ag、 Au的势能曲线和线热膨胀系数随温度的变化进行定量计算。 需要说明的是, 为了便于与实验结果比较, 本文仅给出自然态FCC-Cu、 Ag、 Au的计算结果。

7.1 理论势能曲线

根据MAI势能函数, 计算得到FCC-Cu、 Ag、 Au的理论势能曲线, 如见图1所示。

7.2 线热膨胀系数随温度的变化

根据Debye模型和线热膨胀系数Grüneisen公式^[21], 由MAI势能函数计算所得的常数Q₀和k, 结合文献[22]的Debye温度θ_D, 得到FCC-Cu、 Ag、 Au的线热膨胀系数随温度的变化关系曲线如图2所示, 其中实验数据来自参考文献[21]。

8 结论

1) 由纯金属单原子理论OA方法计算了FCC-Cu、 Ag、 Au的电子结构, 发现当自由原子聚合形成FCC-Cu、 Ag、 Au时, 每个原子分别约有0.21, 0.57, 0.90个d电子转化为s电子, 故FCC-Cu、 Ag、 Au的电子结构可以依次描述为: (FCC-Cu)=[Ar](3d_n)^5.58 (3d_c)^4.21 (4s_c)^0.23 (4s_f)^0.98 , ψ(FCC-Ag)=[Kr](4d_n)^4.87(4d_c)^4.56(5s_c)^0.66(5s_f)^0.91, ψ(FCC-Au)=[Xe] (5d_n)^4.20(5d_c)^4.90 (6s_c)^1.57(6s_f)^0.33。

2) 根据自然态FCC-Cu、 Ag、 Au的电子结构定性解释了物理性质差异与电子结构的关系; 定量计算了晶格常数、 结合能、 势能曲线和线热膨胀系数随温度的变化, 这些性质的理论值和实验值吻合较好。

3) 根据SGTE纯单质数据库的热力学数据, 结合实验外推的晶格常数, 由OA方法计算了非自然态的电子结构, 并定性解释了晶体结构BCC和HCP的关系, 所确定的非自然态电子结构结果分别为: ψ(HCP-Cu)=[Ar](3d_n)^6.00(3d_c)^4.00 (4s_c)^0.3 (4s_f)^0.68,ψ(HCP-Ag)=[Kr](4d_n)^5.78(4d_c)^3.22(5s_c)^1.89(5s_f)^0.11,ψ(HCP-Au)=[Xe](5d_n)^6.00 (5d_c)^3.02 (6s_c)^1.83(6s_f)^0.15; ψ(BCC-Cu)=[Ar](3d_n)^5.26(3d_c)^4.37 (4s_c)^0.08 (4s_f)^1.29, ψ(BCC-Ag)=[Kr](4d_n)^5.75(4d_c)^3.29(5s_c)^1.84(5s_f)^0.13,ψ(BCC-Au)=[Xe](5d_n)^4.00(5d_c)^5.18 (6s_c)_1.20(6s_f)_0.62; ψ(L-Cu)=[Ar](3d_n)^4.35(3d_c)^4.65 (4s_f)^2.00, (L-Ag)=[Kr](4d_n)^4.76(4d_c)^4.43 (5s_f)^1.81, ψ(L-Au)=[Xe](5d_n)^5.80(5d_c)^3.33 (6s_c)^1.76(6s_f)^0.10。

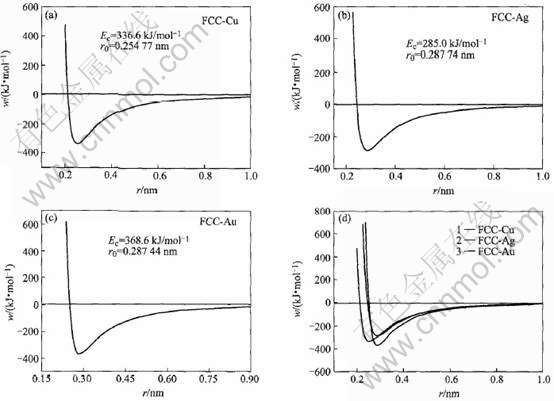
图1 贵金属Cu(a)、 Ag(b) 和Au(c)的理论势能曲线及对比(d)

Fig.1 Theoretical potential curves of noble metal Cu(a), Ag(b), Au(c) and their comparison(d)

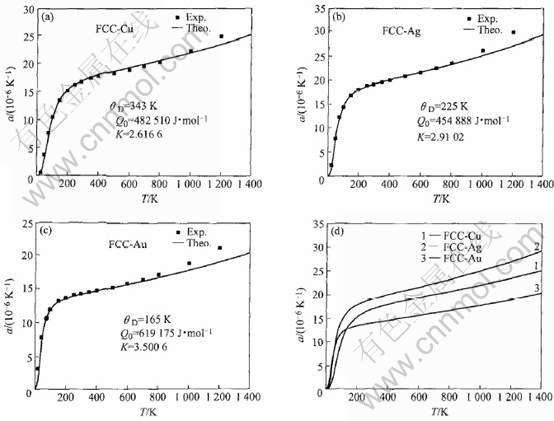
图2 贵金属Cu(a)、 Ag(b)和Au(c)线热膨胀系数随温度变化及其对比图(d)

Fig.2 Linear thermal expansion variation with temperature of noble metals Cu(a), Ag(b), Au(c) and their comparison(d)

REFERENCES

[1]谢佑卿, 彭坤, 刘心笔, 等. 无序HCP TixAl_1-x合金的单原子操纵设计[J]. 中国有色金属学报, 2002, 12(2): 205-212.

XIE Yon-qing, PENG Kun, LIU Xin-bi, et al. Monoatom control designing of disordered HCP TixAl_1-x alloy[J]. The Chinese Journal of Nonferrous Metals, 2002, 12(2): 205-212.

[2]XIE You-qing, TAO Hui-jin, PENG Hong-jian, et al. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC TiAl₂ type alloys[J]. Physica B, 2005, 366: 17-37

[3]PENG Kun, XIE You-qing, PENG Hao, et al. Structures and properties of Sc and Y metals[J]. Journal of Central South University of Technology, 2000, 7(3): 136-139.

[4]XIE You-qing, PENG Kun, YANG Xin-xin. Electronic structures and properties of Ti, Zr and Hf metals[J]. Journal of Central South University of Technology, 2001, 8(2): 83-88.

[5]HE Yu, XIE You-qing. Electronic structures and properties of V, Nb and Ta metals[J]. Journal of Central South University of Technology, 2000, 7(1): 7-11.

[6]XIE You-qing. A new potential function with Many-Atom interactions in solid[J]. Science in China(series E) , 1993, 36(1): 90-99.

[7]XIE You-qing. Relationship of Lennard-Jones potential and Morse potential with W_x(r) potential[J]. Trans Nonferrous Met Soc China, 1994, 4(1): 63-66.

[8]XIE You-qing, ZHANG Xiao-dong, ZHAO Li-yin, et al. Electronic structure and properties of Cu metal[J]. Science in China(series A), 1993, 36(4): 487-494.

[9]XIE You-qing, MA Liu-yin, ZHANG Xiao-dong, et al. Microstructure and properties of Au-Ni alloys[J]. Science in China(series A) , 1993, 36(5): 612-623.

[10]XIE You-qing. Electronic structure and properties of pure iron[J]. Acta Metallurgica Materialia, 1994, 42(11): 3705-3715.

[11]XIE You-qing. Atomic energies and Gibbs energy functions for Ag-Cu alloys[J]. Science in China(series E) , 1998, 41(2): 146-156.

[12]XIE You-qing, ZHANG Xiao-dong. Atomic volumes and volume functions for Ag-Cu alloys[J]. Science in China(series E) , 1998, 41(2): 157-168.

[13]XIE You-qing, ZHANG Xiao-dong. Electronic structure of Ag-Cu alloys[J]. Science in China(series E) , 1998, 41(3): 225-236.

[14]XIE You-qing, ZHANG Xiao-dong. Phase diagram and thermodynamic properties of Ag-Cu alloys[J]. Science in China(series E) , 1998, 41(4): 348-356.

[15]Xie Y Q, Peng K, Liu X B. Influences of xTi/xAl on atomic states, lattice constants and potential-energy planes of ordered FCC TiAl-type alloys[J]. Physica B, 2004, 344: 5-20.

[16]Xie Y Q, Liu X B, Peng K, et al. Atomic states, potential energies, volumes, stability, and brittleness of ordered FCC TiAl₃-type alloys[J]. Physica B, 2004, 353: 15-33.

[17]Xie Y Q, Peng H J, Liu X B, et al. Atomic states, potential energies, volumes, stability and brittleness of ordered FCC Ti₃Al-type alloys[J]. Physica B, 2004, 362: 1-17.

[18]YU Fang-xin, XIE You-qing, NIE Yao-zhuang. Electronic structure of Au-Au alloys[J]. Trans Nonferrous Met Soc China, 2004, 14(6): 1041-1049.

[19]谢佑卿. Au-Au合金系中无序和有序相的晶格常数[J]. 金属学报, 1998, 34(12): 1233-1242.

XIE You-qing. Lattice constants of disordered and ordered phases in the Au-Cu system[J]. Acta Metallurgica Sinica, 1998, 34(12): 1233-1242.

[20]谢佑卿, 张晓东. Au-Au合金的微观结构和性质[J]. 金属学报, 1994, 30(12): 531-539.

XIE You-qing, ZHANG Xiao-dong. Microstructure and properties of Au-Cu alloys[J]. Acta Metallurgica Sinica, 1994, 30(12): 531-539.

[21]American Institute of Physics. American Institute of Physics Handbook, 3rd ed[M]. New York: McGraw-Hill Book Company, 1972. 9-5-9-7.

[22]Kittel C. Introduction to Solid State Physics, 6th ed[M]. New York: John Wiley & Sons, Inc, 1986. 55, 57, 144, 110.

[23]Dinsdale A T. SGTE data for pure elements[J]. Calphad, 1991, 15(4): 317-425.

[24]Saunders N, Miodowik A P, Dinsdale A T. Metastable lattice stability for the elements[J]. Calphad, 1988, 12(4): 351-374.

[25]Weast R C. CRC Handbook of Chemistry and Physics[M]. 70th ed. Florida: CRC Press Inc, 1990. B-215, 216.

[26]Grigorovich V K. The Metallic Bond and Structure of Metals[M]. New York: Nova Science, 1989.

[27]ASM International Handbook Committee. Metals handbook(vol 2): Properties and Selection: Nonferrous Alloys and Special-purpose Materials[M]. 10th ed. OH: Materials Park, 1990. 1113, 1117, 1157.

[28]Kirby R K, Hahn T A, Rothroch B D. Thermal expansion[A]. American Institute of Physics Handbook[C]. New York: McGraw-Hill Book Company, 1972.4-119-4-138.

基金项目: 国家自然科学基金资助项目(50271085), 湖南省自然科学基金重大项目(99JZY1005)

收稿日期: 2005-09-30; 修订日期: 2006-01-21

通讯作者: 陶辉锦; 电话: 0731-8879287; E-mail: taohuijin@hotmail.com

(编辑何学锋)