J. Cent. South Univ. Technol. (2011) 18: 1256-1262

DOI: 10.1007/s11771-011-0830-3

Coupled thermo-hydro-mechanical-migratory model for dual-porosity medium and numerical analysis

ZHANG Yu-jun(张玉军)¹, YANG Chao-shuai(杨朝帅)²

State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics,

Chinese Academy of Sciences, Wuhan 430071, China

? Central South University Press and Springer-Verlag Berlin Heidelberg 2011

Abstract: A coupled thermo-hydro-mechanical-migratory model of dual-porosity medium for saturated-unsaturated ubiquitous-joint rockmass was established, in which the stress field and the temperature field were single, but the seepage field and the concentration field were double, and the influences of sets, spaces, angles, continuity ratios, stiffnesses of fractures on the constitutive relationship of the medium were considered. Also, the relative two-dimensional program of finite element method was developed. Taking a hypothetical nuclear waste repository as a calculation example, the case in which the rockmass was unsaturated dual-porosity medium and radioactive nuclide leak was simulated numerically, and the temperatures, negative pore pressures, saturations, flow velocities, nuclide concentrations and principal stresses in the rockmass were investigated. The results show that the negative pore pressures and nuclide concentrations in the porosity and fracture present different changes and distributions. Even though the saturation degree in porosity is only about 1/10 that in fracture, the flow velocity of underground water in fracture is about three times that in porosity because the permeability coefficient of fracture is almost four orders higher than that of porosity. The value of nuclide concentration in fracture is close to that in porosity.

Key words: ubiquitous-joint rockmass; dual-porosity medium; thermo-hydro-mechanical-migratory coupling model; numerical analysis

1 Introduction

Some countries like China, Japan, Sweden, Switzerland and Canada plan to carry out geological disposal for high-level radioactive nuclear waste in granite body, and now the related studies are underway. The United States has completed the Drift Scale Test in tuff located in Nevada, and prepared to build the first geological disposal repository for high-level radioactive nuclear waste in the world in Yucca Mountain [1-2]. As the medium of high-level radioactive geological disposal waste, the granite and tuff have some advantages including large scale of rockmass, high strength, high thermal conductivity and stability, good absorbability and retardation capability of radioactive nuclide and so on; but they also have some distributed joints and fractures with variable lengths and densities which promote the flow of groundwater [3]. The media resembling granite and tuff, which are ubiquitous-jointed and have both pore and fracture in themselves, are called dual-porosity media.

For the interaction among temperature field, stress field, seepage field and solute migration in porous medium, a number of multi-field coupling problems have been studied. For instance, considering the effect on concentration contribution of nuclides due to variable density groundwater flow, LING et al [4] developed a coupled numerical model describing the transportation of radionuclides in matrix-fracture media. Based on the differential control equations of the coupled thermo- hydro-mechanical (THM) processes of dual media, ZHAO et al [5] presented a three-dimensional coupled model of dual media to study the coupled THM processes in fractured rock masses, and developed a three-dimensional FEM code for analysis of coupled THM processes of dual media. LIU et al [6] established an iterative computation model for the analysis of water flow coupled with stress, adopting the element-by- element (EBE) finite element parallel computation method for numerical simulation.  Adopting a double structure approach based on two superimposed domains, OLIVELLA et al [7] presented the THM analyses to simulate the drift scale test (DST) performed at Yucca Mountain. RUTQVIST and TSANG [8] developed a program, TOUGH-FLAC, in which a double permeability model is used to simulate the rock mass consisting of matrix continuum and fractured continuum. SONNENTHAL et al [9] performed thermo-hydro- chemical simulations using TOUGHREACT code, which includes the coupling among heat, water and vapor flow, aqueous and gaseous species transport, kinetic and equilibrium mineral-water reactions, and feedback of mineral precipitation/dissolution on porosity, permeability and capillary pressure. However, all these researches are limited to hydro-migratory coupling, hydro-mechanical coupling, thermo-hydro-migratory (chemical) coupling, and thermo-hydro-mechanical coupling. The fully coupled thermo-hydro-mechanical- migratory (THMM) model has not been developed for dual-porosity media.

The study of coupled thermo-hydro-mechanical- migratory model and numerical method for the ubiquitous-jointed rock mass called dual-porosity media not only is a practical need in high-level radioactive geological disposal waste engineering, but also is a basic, prospective, and innovative scientific subject. For this reason, against the insufficiencies in the above- mentioned studies and on the basis of existing research results [10-11], firstly, the mathematical model for thermo- hydro-mechanical-migratory coupling process in dual-porosity media is theoretically put forward. Secondly, a relative two-dimensional elastic-plastic FEM program is developed with independent intellectual property right. And then, taking a hypothetical nuclear waste repository located in an unsaturated dual-porosity rock mass as the calculation example, and assuming certain initial conditions of temperature, pore water pressure, in-situ stress and nuclide release intensity, the distributions and changes of temperatures, pore pressures, flow velocities of groundwater, nuclide concentrations and normal stresses in the near field of the repository are investigated.

2 Thermo-hydro-mechanical-migratory coupling equations for dual-porosity media

For the dual-porosity medium shown in Fig.1, it can be thought that there exist pore water pressure and fracture water pressure, pore concentration and fracture concentration, but the stress field and temperature field are single in the medium [12-14]. So, one kind of three- dimensional model for coupled thermo-hydro- mechanical-migratory process is created. By omitting the complex deriving steps, the governing equations are given as follows.

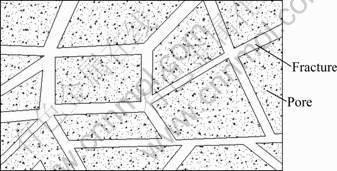
Fig.1 Porous-fractured media

2.1 Equilibrium stress equation

Supposing there are n sets of fractures in a fractured porous rock mass, the equilibrium stress equation can be written in the global coordinate system as [15]

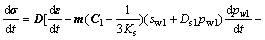
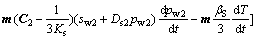 (1)

where σ and ε are the total stress and total stain, respectively; D=(C₁+C₂)^-1 is the elastic matrix; m^T=   [1 1 0], is the unit normal column matrix; K_s, β_S and T are the bulk modulus, synthesized thermal expansion coefficient and temperature of the fractured porous rock mass, respectively; s_w1, p_w1, D_s1, C₁ and s_w2, p_w2, D_s2, C₂ are the saturation degree, water pressure, specific moisture content and flexibility matrix of rock matrix and fractured network, respectively; t is the time.

2.2 Continuity equation for groundwater

On the basis of the principle of mass balance, the water volume flowing into an object during a time increment of dt is equal to the rate of water accumulation within the object. Assuming that the seepage of water can be expressed by Darcy’s law, the continuity equation for rock matrix is expressed by

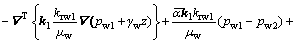
  (2)

where k₁ and k_rw1 are the intrinsic permeability tensor and relative permeability of rock matrix, respectively; ρ_w, μ_w, and γ_w are the density, dynamic viscosity and unit weight of water, respectively; z is the head above some arbitrary datum; 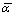 is a coefficient which depends on the fracture width and geometry; k_w is the bulk modulus of water; β_w is the thermal coefficient of water; D_tl is the thermal water diffusivity of rock matrix; A₁, B₁, E₁ and F₁ are the constant matrixes.

For the fractured medium, the continuity equation of groundwater is

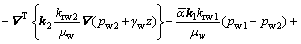
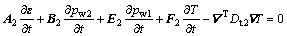  (3)

where k₂ and k_rw2 are the intrinsic permeability tensor and relative permeability of fractured medium, respectively; A₂, B₂, E₂ and F₂ can be obtained by replacing subscripts 1 and 2 in expressions of A₁, B₁, E₁ and F₁; D_t2 is the thermal water diffusivity of fractured medium.

2.3 Energy conservation equation

In accordance with the principle of energy conservation, the rate of heat flow into an object equals the increase of the internal energy within the object. The energy conservation equation takes the form of

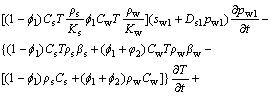
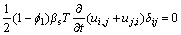                       (4)

where C_w is the specific heat of water; C_s, ρ_s and λ are the specific heat, density and thermal conductivity matrix of fractured porous rock mass, respectively; 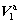 and  are the apparent flow velocities of pore water and fracture water, respectively; u_i and u_j are the displacement components; δ_ij is the Kronecker’s delta.

2.4 Percolation-migration equation

According to Ref.[16], the percolation-migration equation is introduced for porous rockmass and fractured network as

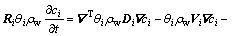
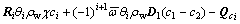      (5)

where i=1, 2, corresponding to rock matrix and fractured network, respectively; R_i is the retardation coefficient; V_i is the apparent velocity of groundwater; θ_i is the volumetric water content; ρ_w is the water density; D_i is the diffusion tensor; c_i is the concentration of solute; χ is the radioactive decay constant; 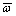 is the coefficient which depends on the fracture width and geometry; Q_ci is the source term.

By means of the Galerkin method, the finite element discretization in both space and time domain is carried out for the equilibrium equation, the continuity equation, the energy conservation equation and the percolation- migration equation. The corresponding finite element scheme can also be obtained.

3 Verification of coupling model for dual- porosity media

For the above-mentioned thermo-hydro-mechanical- migratory coupling model for the dual-porosity media, a two-dimensional FEM code was developed. The rationality of the model and code is verified as follows.

Because there is no analytic solution for thermo-hydro-mechanical-migratory coupling which can be used as a standard of comparison up to now, and it is difficult to find the suitable in-situ test data for simulation at this time, we try to utilize the existing numerical solution for proving the model. ELSWORTH put forward a coupled hydro-mechanical model for dual-porosity media. As an examination example, it is assumed that a well-distributed loading p₀ acts on the top of a one-dimensional saturated column containing orthogonal fractures of uniform spacing of 0.1 m, and the hydrologic-mechanical properties of material are given in Table 1. A numerical simulation of hydro-mechanical coupling for the column was executed by using the relative FEM software, and the computation results complied with the objective laws [17]. In order to compare the coupled thermo-hydro-mechanical- migratory model with ELSWORTH’s model, a FEM analysis of  hydro-mechanical coupling for the same column, in which the temperature is a constant and the solute migration is not considered temporarily, was also made. The fluid pressure responses with depth of the column obtained by ELSWORTH and in this work are illustrated in Fig.2, and the corresponding surface settlement associated with the expulsion of fluid from the dual-porosity system is represented in Fig.3. It can be seen that the simulation results by two computation programs are really close, indicating that the model established in this work is reliable.

Table 1 Column coefficients

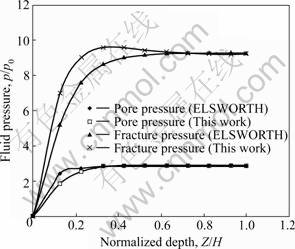
Fig.2 Pore pressure equilibration responses for one- dimensional column loaded axially at 4 000 s

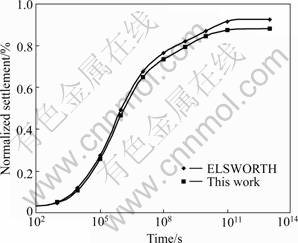
Fig.3 Surface settlements versus time for one-dimension column loaded

4 Computation example

As shown in Fig.4, it is assumed that a canister filled with the vitrified radioactive nuclear waste is disposed at the depth of 500 m beneath the ground surface. As an approximate simplification, it is treated to be a plane strain problem. A computation region with a horizontal length of 4 m and a vertical length of 8 m is taken. There are 800 elements and 861 nodes in the mesh. The node numbers are 432, 433, 434 and 435 from the outer margin of waste canister to the right. The rock mass is an unsaturated medium, in which there exist one set of horizontal fracture and one set of vertical fracture which are orthogonal. Referring to the rockmass situations of DST test performed at Yucca Mountain in USA [18], the relative calculating parameters are presented in Tables 2 and 3.

Fig.4 FEM mesh

The porous rockmass has a high water content, but the fractured network is quite dry. The initial saturations of the rock matrix and fracture system are 0.9, 0.1 and 0.2, respectively, and their water retention curves conform to the Van Genuchten model, that is

                           (6)

where α, n and m=1-1/n, are the material constants; ψ is the water potential head; s_ws and s_wr are the maximum saturation and the minimum saturation, respectively. For the rock matrix, α=2.25×10^{-6 m-1}, n=1.33, s_ws and s_wr are 1.0 and 0.18, respectively, so the initial pore pressure in rock matrix is -0.34 MPa; for the fracture system, α= 9.74×10^{-6 m-1}, n=1.97, s_ws and s_wr are 1.0 and 0.01, respectively, so the initial pore pressure in fracture system is -0.14 MPa.

The relationship between relative permeability and saturation degree is

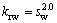                                                                  (7)

Table 2 Main computation parameters for rock and vitrified waste

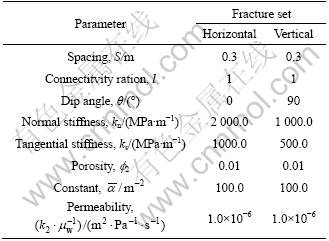
Table 3 Parameters for fracture sets used in calculation

Both of the thermal water diffusivities of the rock matrix and fracture system are taken as D_t=2.0×10^{-5  m2}/(s?°C^-1).

The boundary conditions are as follows. The free displacement and the fixed temperature and pore water pressure are allowed for the top of computation domain on which the vertical stress acts due to the overburden load. Both the left and right sides are fixed displacement-horizontal, adiabatic and impermeable. The vertical displacement of the bottom surface, temperature and pore water pressure are fixed. The initial conditions are that the temperature of rock mass and buffer is a uniform value of 20.0 °C. It is supposed that after finishing embedding of a waste canister, the canister is damaged by some reasons, so that the radioactive nuclides begin to leak out into the near field with a constant concentration and rate from the canister. The time when the nuclides begin to leak out is taken as the starting time of the computation. The temperature in the computation domain is 24 °C (uniformly distributed). The vitrified waste is the source term with a diffusive mass flux of radioactive nuclides of Q_c=1.44×10^-6 mol?kg/(m³?s^-1). The constants used in the computation concerned with the percolation-migration of nuclide are supposed as follows. The tortuosity coefficients, τ₁ and τ₂, are 0.4 and 0.8, respectively; the dispersivities in the longitudinal direction, α_1L and α_2L, are 1.0 and 2.0 m, respectively; the dispersivity in the transversal direction is α_iT=α_iL/10; the molecular diffusion coefficients, α_1m and α_2m, are 1.0×10^-9 and 2.0×10^{-9 m2}/s, respectively; the distribution coefficients, K_d1 and K_d2, are 8.0 and     5.3 mL/g, respectively; the dry densities, ρ_d1 and ρ_d2, are 23.0 and 21.0 kg/m³, respectively; the parameter 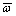 is 100.0 m^-2; the radioactive decay constant χ=ln2/T_half, where T_half is the half life of the nuclide which is taken as 1 000 a in the computation. The waste radiates heat continuously with a power of 300 W during a period of   4 a, and the time step is taken as 100 000 s. The main computation results and analyses are as follows.

In the early 0.15 a, the temperature of buffer increases fast, and then it grows slowly. At the termination of computation, the temperatures of nodes 432, 433, 434 and 435 are 77.9, 63.1, 54.4 and 47.9 °C, respectively.

The pore pressures versus time of nodes 432, 433, 434, 435 are shown in Fig.5, from which it is known that at the beginning stage, the negative pore pressures rise fast, and until approximately 0.15 a, their values tend towards stability; however, the negative fracture pressures decrease rapidly at the early stage, and after about 0.15 a, the values change quite little. Taking node 433 for instance, at the time of 0.01, 0.1 and 4.0 a, the pore pressures are -1.86, -3.17 and -3.34 MPa and the fracture pressures are -0.223, -0.185 and -0.186 MPa, respectively.

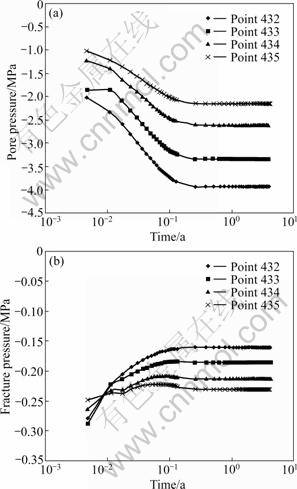
Fig.5 Groundwater pressures versus time in porosity rock mass (a) and fracture system (b)

The saturations of the pore and fracture versus time in calculating domain are similar to those of the corresponding pore and fractured pressure. Taking node 433 for instance, at the time of 0.01, 0.1 and 4.0 a, the degrees of pore saturation are 0.68, 0.60, 0.59 and the degrees of fracture saturation are 0.06, 0.08, 0.08, respectively. The flow velocities of nodes 432, 433, 434, 435 are 1.67×10^-3, 1.54×10^-3, 1.09×10^-3 and 0.83×10^{-3 m/s in pore rock mass and 6.00×10-3}, 5.75×10^-3, 4.13×10^-3 and 2.48×10^{-3 m/s in fracture network, respectively.}

The nuclide concentrations of nodes 432, 433, 434, 435 versus time in pore and fracture are plotted in Fig.6. It is seen that during the first 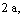 the increasing velocities of nuclide concentrations in the pore matrix are the maximum, and then they grow slowly. Until  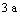they perform a decreasing tendency at node 432 and its adjacent node 432 in margin of canister. However,  during the early 2 a, the growing velocities of nuclide concentrations in fracture network rise quickly, and then they tend towards stability. At the termination of calculating, the flow velocities of nodes 432, 433, 434, 435 are 1.11, 0.68, 0.35, 0.16 mol/m³ in the pore rock mass and 1.20, 0.64, 0.35, 0.12 mol/m³ in the fracture network, respectively.

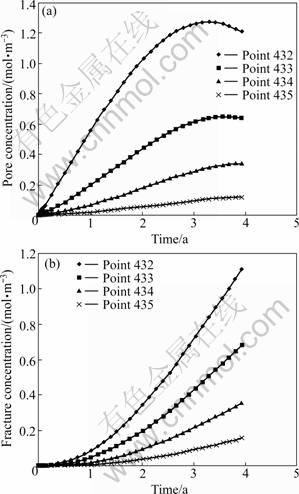
Fig.6 Concentration versus time plots in porosity rock mass (a) and fracture system (b) at different nodes for nuclide with half life of 1 000 a

The stress concentration is significant in vicinity of the canister for the reason that the temperature and pore pressure of this section are relative high. The max/min main stresses of nodes 432, 433, 434, 435 are 1.52/-3.55, 0.67/-3.75 and -0.22/-4.03 MPa, respectively.

5 Conclusions

1) The temperatures in the near field of the repository rise rapidly during 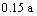 at the beginning, then change quite little. At the end of computation    (4.0 a), the temperatures in the near field can reach 30.0- 80.0 °C.

2) Due to the effect of temperature gradient, the pore water near the waste canister migrates towards both the far field and fractures fast, causing the negative pore pressure in the near field to rise rapidly to a high value (about -3.94 MPa), the saturation of pore to reduce obviously and the corresponding sections become dryer. During the same process, in spite of the fracture water migrating form the near field to the far field, it obtains more recharge from the pore groundwater, causing the negative fracture pressure in the near field to reduce (the mix value is about -0.16 MPa) and the saturation of fracture system to increase moderately. Even though the saturation of pore water is about 10 times the magnitude of the saturation of fracture water, the flow velocities of fracture water are approximately three times those of pore water because the hydraulic conductivity of fracture is almost four orders higher than that of porosity.

3) At the beginning, the increasing velocity of nuclide concentration is the largest. Then, it grows slowly, and until a certain moment, the nuclide concentrations in the near canister do not rise. Due to the nuclide concentration difference between porosities and fractures, the concentration in fractures increases rapidly at the beginning, and then this growth becomes slow, but the concentration always grows and in the end of computation, the value of it in fracture is close to that in porosity.

References

[1] WANG Ju, ZHENG Hua-ling, XU Guo-qing, FAN Xian-hua, WANG Chen-zhu, FAN Zhi-wen. Geological disposal of high level radioactive waste in China: Progress in last decade (1991-2000) [C]// WANG Ju, FAN Xian-hua, XU Guo-qing, ZHENG Hua-ling. Geological Disposal of High Level Radioactive Waste in China: Progress in Last Decade. Beijing: Atomic Energy Press, 2004: 1-12. (in Chinese)

[2] TRW Environmental Safety Systems Inc. Drift scale test progress report No.1 [R]. Las Vegas: TRW Environmental Safety Systems Inc., 1998.

[3] MIN Mao-zhong, XU Guo-qing. Principles for disposal of radioactive waste [M]. Beijing: Atomic Energy Press, 1998. (in Chinese)

[4] LING Bing, LIU lei, XUE Qiang, SUN Wei-ji. Study on numerical simulation of nuclides leakage for groundwater pollution [J]. Journal of System Simulation, 2007, 19(2): 261-311. (in Chinese)

[5] ZHAO Yan-lin, CAO Pong, ZHAO Yang-sheng, LIN Hang, WANG Yi-xian. Dual media model for thermo-hydro-mechanical coupling and 3D numerical simulation [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(Supp.2): 4024-4031. (in Chinese)

[6] LIU Yao-ru, YANG Qiang, HUANG Yan-song, LI Xiao-qin. Parallel numerical analysis of coupled fluid flow and stress based on dual porosity media mode [J]. Chinese Journal of Rock Mechanics and Engineering, 2007, 26(4): 705-711. (in Chinese)

[7] OLIVELLA S, GENS A. Double structure THM analyses of a heating test in a fractured tuff incorporating intrinsic permeability variations [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 667-679.

[8] RUTQVIST J, TSANG C F. Analysis of thermal-hydrologic- mechanical behavior near an emplacement drift at Yucca mountain [J]. Journal of Contaminant Hydrology, 2003, 62/63: 637-652.

[9] SONNENTHAL E, ITO A, SPYCHER N, YUI M, APPS J, SUGITA Y, CONRAD M, KAWAKAMI S. Approaches to modeling coupled thermal, hydrological, and chemical processes in the drift scale heater test at Yucca Mountain [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 698-719.

[10] ZHANG Yu-jun, ZHANG Wei-qing. 2D FEM analysis for coupled thermo-hydro-mechanical-migratory processes in near field of a hypothetical nuclear waste repository [J]. Journal of Central South University of Technology, 2010, 17(3): 612-620.

[11] ZHANG Yu-jun. Model and numerical simulation for coupled thermo-hydro-mechanical-migratory processes considering influence of solute concentration [J]. Rock and Soil Mechanics, 2008, 29(1): 212-218. (in Chinese)

[12] LEIWS R W, SCHREFLER B A. The finite element method in the static and dynamic deformation and consolidation of porous media [M]. Chichester, West Sussex: Wiley, 1998: 307-322.

[13] RUTQVIST J, WU Y S, TSANG C F, BODVARSSON G. A modeling approach for analysis of coupled multiphase fluid flow, heat transfer, and deformation in fractured porous rock [J]. International Journal of Rock Mechanics and Mining Sciences,2002, 39(4): 429-442.

[14] RUTQVIST J, BARR D, DATTA R, GENS A, MILLARD A, OLIVELLA S, TSANG C F, TSANG Y. Coupled thermal- hydrological-mechanical analyses of the Yucca Mountain Drift Scale Test-Comparison of field measurements to predictions of four different numerical models [J]. Int J of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 680-697.

[15] ZHANG Yu-jun. Coupled thermo-hydro-mechanical model and finite element analyses of dual-porosity fractured medium for ubiquitous-joint rock mass [J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28(5): 947-955. (in Chinese)

[16] NISHIGAKI M. Density dependent transport analysis saturated- unsaturated porous media—3 dimensional Eulerian Lagrangian method [R]. Okayama University, 2001.

[17] ELSWORTH D, MAO B. Flow-deformation response of dual-porosity media [J]. Journal of Geotechnical Engineering, 1992, 118(1): 107-124.

[18] RUTQVIST J, BARR D, DATTA R, GENS A, MILLARD A, OLIVELLA S, TSANG C F, TSANG Y. Coupled thermal- hydrological-mechanical analyses of the Yucca Mountain Drift Scale Test—Comparison of field measurements to predictions of four different numerical models [J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(5/6): 680-697.

(Edited by YANG Bing)

Foundation item: Project(2010CB732101) supported by the National Basic Research Program of China; Project(51079145) supported by the National Natural Science Foundation of China

Received date: 2010-07-15; Accepted date: 2010-10-22

Corresponding author: ZHANG Yu-jun, PhD; Tel: +86-27-87198482; E-mail: yjzhang@whrsm.ac.cn