An improved brain emotional learning algorithm for accurate and efficient data analysis
来源期刊:中南大学学报(英文版)2018年第5期
论文作者:谭冠政 梅英
文章页码:1084 - 1098
Key words:prediction; classification; brain emotional learning; genetic algorithm
Abstract: To overcome the deficiencies of high computational complexity and low convergence speed in traditional neural networks, a novel bio-inspired machine learning algorithm named brain emotional learning (BEL) is introduced. BEL mimics the emotional learning mechanism in brain which has the superior features of fast learning and quick reacting. To further improve the performance of BEL in data analysis, genetic algorithm (GA) is adopted for optimally tuning the weights and biases of amygdala and orbitofrontal cortex in BEL neural network. The integrated algorithm named GA-BEL combines the advantages of the fast learning of BEL, and the global optimum solution of GA. GA-BEL has been tested on a real-world chaotic time series of geomagnetic activity index for prediction, eight benchmark datasets of university California at Irvine (UCI) and a functional magnetic resonance imaging (fMRI) dataset for classifications. The comparisons of experimental results have shown that the proposed GA-BEL algorithm is more accurate than the original BEL in prediction, and more effective when dealing with large-scale classification problems. Further, it outperforms most other traditional algorithms in terms of accuracy and execution speed in both prediction and classification applications.
Cite this article as: MEI Ying, TAN Guan-zheng. An improved brain emotional learning algorithm for accurate and efficient data analysis [J]. Journal of Central South University, 2018, 25(5): 1084–1098. DOI: https://doi.org/10.1007/ s11771-018-3808-6.

J. Cent. South Univ. (2018) 25: 1084-1098
DOI: https://doi.org/10.1007/s11771-018-3808-6
MEI Ying(梅英)1, 2, TAN Guan-zheng(谭冠政)1
1. School of Information Science and Engineering, Central South University, Changsha 410083, China;
2. Electrical and Information Engineering College, Hunan University of Arts and Science,Changde 415000, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2018
Abstract: To overcome the deficiencies of high computational complexity and low convergence speed in traditional neural networks, a novel bio-inspired machine learning algorithm named brain emotional learning (BEL) is introduced. BEL mimics the emotional learning mechanism in brain which has the superior features of fast learning and quick reacting. To further improve the performance of BEL in data analysis, genetic algorithm (GA) is adopted for optimally tuning the weights and biases of amygdala and orbitofrontal cortex in BEL neural network. The integrated algorithm named GA-BEL combines the advantages of the fast learning of BEL, and the global optimum solution of GA. GA-BEL has been tested on a real-world chaotic time series of geomagnetic activity index for prediction, eight benchmark datasets of university California at Irvine (UCI) and a functional magnetic resonance imaging (fMRI) dataset for classifications. The comparisons of experimental results have shown that the proposed GA-BEL algorithm is more accurate than the original BEL in prediction, and more effective when dealing with large-scale classification problems. Further, it outperforms most other traditional algorithms in terms of accuracy and execution speed in both prediction and classification applications.
Key words: prediction; classification; brain emotional learning; genetic algorithm
Cite this article as: MEI Ying, TAN Guan-zheng. An improved brain emotional learning algorithm for accurate and efficient data analysis [J]. Journal of Central South University, 2018, 25(5): 1084–1098. DOI: https://doi.org/10.1007/ s11771-018-3808-6.
1 Introduction
Data analysis is an important task of machine intelligence in the field of information and it can extract useful information from large-scale data, which is helpful to provide guidance for the next decision. Nowadays, many artificial intelligence methods have been proposed for classification, pattern recognition, prediction and fitting problems, such as support vector machine (SVM) [1], k-nearest neighbor (k-NN) [2] and artificial neural network (ANN) [3]. Among these methods, ANN is very popular due to the characteristics of self-learning, self-adaptive and high generalization capability. However, the traditional ANNs have been proven to have some significant drawbacks, such as low training speed, high computational complexity and the convergence rate is hard to meet the requirements of real-time applications. To overcome these deficiencies, researchers have to study new neural networks and new machine learning algorithms.
Thanks to the neurobiology and cognition research of emotion, emotional intelligence is playing an important role in artificial intelligence in recent years, and it has attracted an increasing interest around the world. Several bio-inspired brain emotional learning (BEL) models have been proposed and successfully applied in intelligent engineering applications [4, 5]. These BEL models are based on a computational model called amygdala-orbitofrontal model [6], which was inspired by LEDOUX’s anatomical findings [7] of emotional learning mechanism in mammalian brain. BEL-based models mimic the high speed of emotional learning in brain, which have the superior features of fast learning and quick reacting. Thus, they are also widely used in classification, prediction and control applications [8–10].
In amygdala-orbitofrontal model [6], the reward signal plays an important role to adjust the weights of amygdala and orbitofrontal cortex in emotional learning process, but it is not clearly defined so far. Many researchers proposed different versions of BEL models based on amygdala- orbitofrontal model, as well as different reward signal determinations. LUCAS et al [11] proposed the BEL-based intelligent controller (BELBIC) which had been successfully applied in intelligent engineering applications. ABDI et al [12] applied a modified BEL model to predict short-term traffic flow and defined the reward signal as the multiplication of some related weights. CHEN et al [13] presented a BEL-based controller for a four- wheel drive robot. Although these BEL-based models achieved success in the applications, they were based on reinforcement learning to adjust the weights of Amygdala and Orbitofrontal cortex. These methods are model-sensitive and cannot be generalized to other issues. LOTFI et al [14] proposed a novel BEL-based pattern recognizer (BELPR), instead of employing reward-based reinforcement learning, it employed activation functions and target values to update the weights of BEL network in the learning phase. The BELPR can be learned by using pattern-target examples and it is model-free and time-saving. However, the pattern-target learning method reduced the precision of the process, and the performance of accuracy in data analysis needs to be further improved.
In this study, we aim to optimize the BEL network and make it more accurate. Recently, several evolutionary algorithms have been available to apply in optimization problems, such as artificial bee colony algorithm (ABC) [15], differential evolution (DE) [16] and genetic algorithm (GA) [17]. However, the standard ABC suffers from a slow convergence speed for its solution search equation [15]. Although DE is relatively simple and easily to converge, it may easily fall into local minimum in the searching process [18]. GA tends to efficiently explore various regions of the decision space, and find an optimal solution with a high probability [19]. It has been demonstrated that the performance of neural network can be substantially improved by optimizing the weights with GA [20–22] and the learning process of network is regarded as the process of searching for optimum in the weight space. Therefore, the present work intends to integrate GA with the novel BEL neural network to determine properly weights of the network. The integrated algorithm named GA-BEL takes advantage of the fast learning and low computational complexity of BEL, as well as the global optimum solution of GA. Thus, GA-BEL is expected to achieve better performance than the original BEL in data analysis. The GA-BEL has been tested on a chaotic time series of geomagnetic index for real-world prediction, eight datasets of benchmark university California at Irvine (UCI) and a functional magnetic resonance imaging (fMRI) dataset for classifications. The comparisons of experimental results indicate the superiority of the proposed GA-BEL in terms of accuracy and execution speed.
2 Related works
2.1 Anatomical foundation
The limbic system theory [23] is the neural basis for emotional brain studies. Figure 1(a) [14] shows the limbic system in the brain and its components, including the sensory cortex, thalamus, amygdala, orbitofrontal cortex etc. There are two main parts among these components. One is amygdala, which is properly situated to reach the emotional stimulus and plays a pivotal role in emotional learning process. Another is orbitofrontal cortex, which assists amygdala to process emotional stimulus. LEDOUX [7] stated that emotional stimuli can reach amygdala by two different paths, as shown in Figure 1(b). One is long and precise path, coming from the sensory cortex, and another is short but imprecise path, coming directly from the Thalamus. LEDOUX [7] argued that due to the existence of short path in the emotional brain, emotional stimuli were processed much faster than normal stimuli.

Figure 1 Limbic system and emotion circuits in brain
2.2 Previous BEL model
Motivated by LEDOUX’s anatomical findings [7] in the mammalian brain, MOR N and BALKENIUS [6] firstly proposed the amygdala- orbitofrontal model in 2000 and the framework of amygdala-orbitofrontal model is shown in Figure 2. In amygdala-orbitofrontal model, amygdala and orbitofrontal cortex are two crucial parts of emotional learning and reacting. Amygdala receives emotional stimuli from the Sensory cortex and Thalamus as well as the external reward signal, and it interacts with the orbitofrontal cortex and reacts to the emotional stimuli based on the reward signal. The orbitofrontal cortex receives sensory input from the sensory cortex and evaluates the amygdala’s response to prevent inappropriate learning connections. They interact frequently to mimic the functionality of the emotional brain responsible for processing emotional stimulus.
N and BALKENIUS [6] firstly proposed the amygdala- orbitofrontal model in 2000 and the framework of amygdala-orbitofrontal model is shown in Figure 2. In amygdala-orbitofrontal model, amygdala and orbitofrontal cortex are two crucial parts of emotional learning and reacting. Amygdala receives emotional stimuli from the Sensory cortex and Thalamus as well as the external reward signal, and it interacts with the orbitofrontal cortex and reacts to the emotional stimuli based on the reward signal. The orbitofrontal cortex receives sensory input from the sensory cortex and evaluates the amygdala’s response to prevent inappropriate learning connections. They interact frequently to mimic the functionality of the emotional brain responsible for processing emotional stimulus.

Figure 2 Framework of amygdala-orbitofrontal model
In amygdala-orbitofrontal model, Si is sensory input; Aj is the internal output of the amygdala; Oj is the internal output of the orbitofrontal cortex. The reward signal Rew is used to update weights of amygdala and orbitofrontal cortex in emotional learning, and the learning rules are expressed as follows [6]:
 (1)
(1)
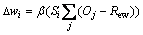 (2)
(2)
where △vi and △wi represent the weights of amygdala and orbitofrontal cortex, respectively; α and β are learning rates, which are used to adjust the learning speed. The reward signal Rew is used to adjust the weights in the emotional learning process.
Various modified BEL models that are based on amygdala-orbitofrontal model have been proposed [11, 13], as well as the reward signal determination. In Ref. [12], the reward signal Rew is defined as:
 (3)
(3)
where rj stands for the factor of the reinforcement agent and wj represents the related weight.
CHEN et al [13] proposed a BEL controller for a four-wheel drive robot and the reward signal Rew is defined as:
 (4)
(4)
where r1, r2, r3 stand for the factors of weights; e represents the error.
Although these BEL models achieved success in the special applications, they applied reward- based reinforcement learning to adjust the weights of amygdala and orbitofrontal cortex, and they were model-sensitive and cannot be generalized to other issues.
LOTFI et al [14] firstly proposed the model- free version of BEL-based pattern recognizer, which employed the target value (T) of input pattern in the learning phase and the reward signal Rew is defined as follows:
 (5)
(5)
Thus, the supervised learning rules in BEL model are described as follows:

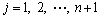 (6)
(6)

 (7)
(7)
where vk j and wk j represent the weights of amygdala and orbitofrontal cortex, respectively; Tk is the target value associated with the kth input pattern Pk; Ek a is the internal output of amygdala; Ek is the final output of the BEL model; γ is the decay rate in the amygdala learning rule; α and β are learning rates. The model can be employed to learn the pattern-target relationship of an application by using BEL algorithm, but this method reduces the precision of the process. Thus, we employed GA to optimally tune the weights of BEL neural network. At the same time, we improved BEL neural network for prediction and classification applications.
3 Implementation
3.1 Single-output BEL neural network for prediction
In contrast to the previous BEL-based models, in this study, we applied fitness function in GA instead of reward-based reinforcement learning to update the weights of amygdala and orbitofrontal cortex in emotional learning. Therefore, motivated by the network in Ref. [9], we deleted the reward signal in the BEL neural network. In addition, according to the biological interaction between amygdala and orbitofrontal cortex in the emotional learning, we added the bias for each part to make the model more accurate. The improved BEL-based neural network is shown in Figure 3. Similar to the amygdala-orbitofrontal model, it consists of four common components including thalamus, sensory cortex, orbitofrontal cortex and amygdala. Amygdala and orbitofrontal cortex are the two main parts, which are mainly responsible for emotional learning and response.
The model is presented as multi-input single- output architecture, amygdala receives m input patterns S=[S1, S2, …, Sm] from the Sensory cortex and Ath from the thalamus. Ath is calculated by
 (8)
(8)
As shown in Figure 3, vi is the amygdala weight and ba is the bias of amygdala neuron. For each sensory input, there is an amygdala node Ai to receive. EA is the internal output of the amygdala and it is calculated by
 (9)
(9)
 (10)
(10)
For each sensory input, there is an orbitofrontal cortex node Oi to receive. EO is the output of the orbitofrontal cortex that is used to inhibit the amygdala’s output, which is calculated by
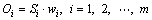 (11)
(11)
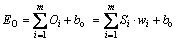 (12)
(12)
where wi represents orbitofrontal cortex weight; bo represents the bias of orbitofrontal cortex neuron.

Figure 3 Improved single-output BEL network for prediction
Finally, the final output is simply calculated by
 (13)
(13)
where E is the final output that represents the correct response of amygdala.
In the single-output BEL neural network, the number of input patterns determines the neurons number in the thalamus and sensory cortex units. The BEL neural network can be learned by pattern-target examples and it is model free and can be utilized in prediction application.
3.2 Multiple-output BEL neural network for classification
The single-output BEL neural network can be extended to multiple-output network for classification. The number of sample classes determines the number of orbitofrontal cortex and amygdala units. Thus, the extended BEL model can be applied in binary and multiple classifications. In the proposed m–n architecture as shown in Figure 4,m represents the number of input features; n represents the number of sample classes; each amygdala-orbitofrontal cortex unit interacts separately in the learning process.
In this study, the weights and biases of amygdala and orbitofrontal cortex in BEL neural network is optimized by GA. The data analysis with GA-BEL can be divided into three parts: BEL neural network structure determination, parameters optimization and prediction or classification output of BEL neural network.
3.3 Optimizing BEL neural network with GA
1) Chromosome representation
For the advantage of high precision, real encoding is adopted to acquire optimal results. One real number string represents one chromosome, which consists of connection weights and biases of orbitofrontal cortex and amygdala. According to the structure of BEL neural network, each chromosome is initialized as follows [9]:
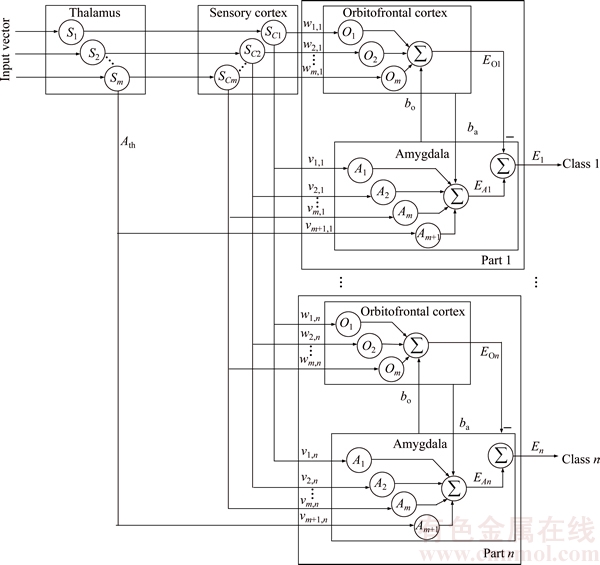
Figure 4 Improved multiple-output BEL network for classification
 (14)
(14)
where wm and bo represent orbitofrontal cortex weights and bias, respectively; vm and ba represent amygdala weights and bias, respectively. The values of the weights and biases are chosen in [–1, 1]; m is the number of input features; the number of genes in each chromosome is 2m+3.
2) Fitness function
Fitness function is used to evaluate the adaptability of each individual in the whole population, and the individual fitness will provide reference to selection operation. The learning process aims to minimize the total error for all training samples. As a consequence, we select the root mean squared error as the evaluation criterion of weights, and the fitness function is defined as
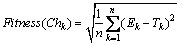 (15)
(15)
where Ek is the response to the kth input pattern with given weights and biases in Chk, which can be calculated by Eq. (13); Tk is the target value of kth input pattern; n is the number of pattern-target pairs.
3) Operations
(a) Selection. To choose better individual for subsequent iteration, we adopt the roulette wheel selection scheme [18]. The fitness of each individual corresponds to the proportion of selection. There are three steps: Firstly, find out the best chromosome and the worst chromosome in the current generation according to the fitness value. Secondly, copy the best individual if it is better than the best individual from the previous generation. At last, replace the worst individual with the best one from the previous generation. The selection probability pi for each individual i is given as follows:
 (16)
(16)
where Fi is the fitness value of individual i; k is the coefficient; n is the number of individuals in a group.
(b) Crossover. To enlarge the diversity and searching space, the crossover operation is needed to produce two new individuals by exchanging information between the parent individuals [24]. We defined the crossover rules as follows:
 (17)
(17)
where ck i and ck j represent the chromosomes which occur crossover in the kth bit; n denotes the number of iterations; α is a random number uniformly distributed in [0, 1].
(c) Mutation. To further enlarge the searching space, mutation is another way to create new individual. Mutation operation is needed to change one or some gene values of chromosome. The method of mutation is given as follows:
 (18)
(18)
where cj i(g) represents the chromosome which occurs mutation in the jth bit; cmax is the upper limit of allele; cmin is the lower limit of allele; g represents current generation; Gmax is the maximum iteration; r1 and r2 are random numbers within the range [0, 1].
After the operations of selection, crossover and mutation, the best chromosome can be found which represents the best combination of weights and biases in BEL network. The original weights and biases will be updated by the genes of the best chromosome, and the trained BEL network can be used for data analysis.
The pseudo-code of GA-BEL is given as follows:
begin
t←0; /* t represents the number of current
generation*/
Initialize genetic parameters, cmax, cmin, Gmax, etc.;
Initialize a population P(t) of chromosomes defined in Eq. (14);
for i=1:m /*m represents the number of samples*/
Calculate BEL network output according to Eq. (8)–Eq. (13);
Evaluate the fitness of P(t) according to Eq. (15);
Obtain the best found result from P(t);
while termination criterion is not fulfilled do
t←t+1;
Select P(t) from P(t-1) by selection process according to Eq. (16);
Alter P(t) by crossover according to Eq. (17) based on the crossover probability;
Mutate offspring according to Eq. (18) based on the mutation probability;
Update the weights and biases of the BEL network;
Calculate BEL network output according to Eq. (8)–Eq. (13);
Evaluate the new fitness function of P(t) according to Eq. (15);
Obtain the best found result from P(t) and compare with P(t–1);
Replace the worst chromosome of P(t) with the best result of P(t–1);
end while
Output the best chromosome;/* The best chromosome represents the combination of the best weights and biases in BEL network according to Eq.(14)*/
end
4 Simulation results
In this section, two case studies are constructed to evaluate the performance of the proposed GA-BEL algorithm. The first experiment is built to show the performance of GA-BEL in prediction. The second experiment is arranged to test the GA-BEL on classification. The comparative experiments are also carried out in the two cases. Both experiments are performed in MATLAB R2013a running in Intel core-i7 3.4GHz CPU with 8.00 GB RAM and Windows 7 operation system.
4.1 Case 1: Experimental results on prediction
4.1.1 Dataset description
In this work, one real-world prediction problem has been studied. The geomagnetic storm disturbs the earth’s magnetosphere and causes harmful damage to the ground-based communication. Therefore, it is essential to predict the geomagnetic activity indices for alert systems development. The disturbance storm time (Dst) index [25] is one of the main indices of geomagnetic storms, which is usually defined to measure the intensity of geomagnetic storms. Dst is a chaotic time series which has been utilized by many data-driven models and it can be downloaded from the World Data Center for Geomagnetism, Kyoto, Japan. Here, 1000 pattern-target pairs of hourly Dst index in year of 2000 are used for online prediction.
4.1.2 Performance evaluation
Prediction performance can be evaluated by mean squared error (MSE) and linear correlation coefficient (R), which are expressed as follows [14]:
 (19)
(19)
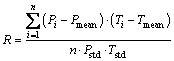 (20)
(20)
The single-output BEL neural network in Figure 3 can be used in time series prediction problems. In this study, we considered the first four-sequence samples as input patterns, and the 5th sequence as the target pattern. Consider the following time series: Dst1, Dst2, Dst3,…, Dstt, …, Dstt+1 is the predicted value at time t+1 which can be calculated by
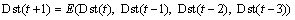 (21)
(21)
where E is the final output of single-output BEL neural network which can be calculated by Eq. (13).
4.1.3 Results and discussions
The single-output BEL neural network can be used in time series prediction problems. For the BEL network, there are four features as sensory input, and one output of amygdala-orbitofrontal cortex unit. Thus, the input nodes, hidden nodes and output node are set to 4, 3, 1, respectively. The initial weights and biases of amygdala and orbitofrontal cortex units are randomly selected between [–1, 1]. In GA, the population groups are set to 200 and each population size is set to 11; the maximal generation is set to 100; the crossover and the mutation rates are 0.8 and 0.001, respectively. Finally, the results of prediction for the Dst index are presented in Figure 5.
Figure 5(a) shows the MSE corresponding to each epoch during the evolution. As illustrated in Figure 5(a), the best MSE is obtained at 100 epoch after the process is in steady state. Figure 5(b) illustrates the predicted versus desired output of the Dst index. Target on the X-axis represents the desired output. Output on the Y-axis represents the actual output of the GA-BEL model. The linear relationship between target and output is also given on the left side. As illustrated in Figures 5(b) and (c), the values of R are 0.95897 and 0.97128 in the training and testing samples, respectively. It indicates that the linear correlation between the output and the desired value is very good in the testing samples.
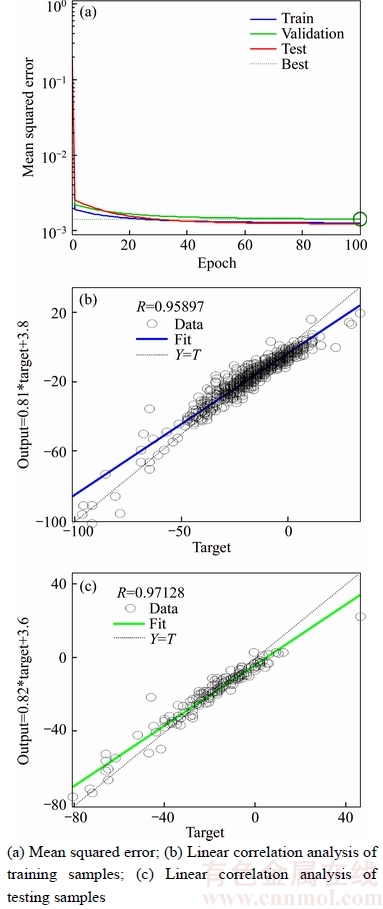
Figure 5 Prediction results of Dst index with GA-BEL
For comparison, we apply the original BEL to test on the same Dst index dataset. Figure 6 presents the prediction results in steady states.
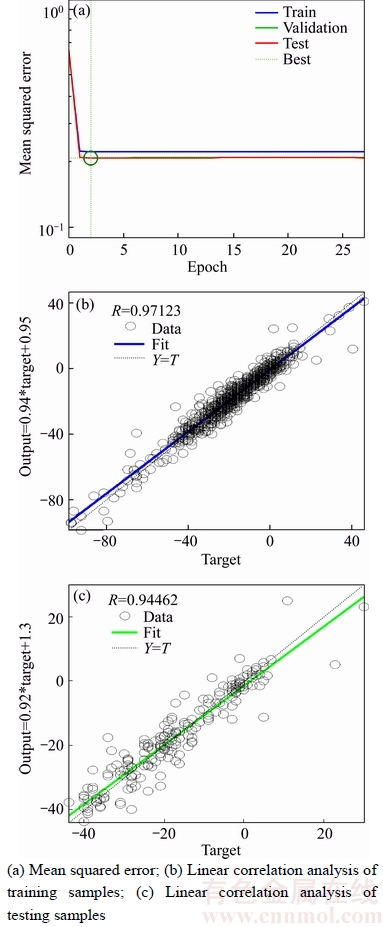
Figure 6 Prediction results of Dst index with BEL
As illustrated in Figure 6(a), the best MSE is obtained at epoch 2. After the process is in steady state, Figure 6(b) illustrates the predicted versus desired output of the Dst index. As illustrated in Figure 6(b), the BEL obtained R=0.94462 in testing samples, which is much less than R=0.97128 of GA-BEL in testing samples.
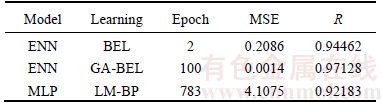
We also compared GA-BEL with the traditional multilayer perceptron (MLP) [26].Table 1 presents the detailed MSE and R obtained from the GA-BEL, BEL and LM-BP in the testing samples. It is obvious that fast training is the main feature of BEL-based algorithms compared to LM-BP algorithm [26]. Although the original BEL needs less epochs to reach the steady state, GA-BEL achieves higher correlation and lower mean square error, which implies that GA-BEL is more accurate than BEL in prediction.
Table 1 Comparisons of GA-BEL, BEL and LM-BP on Dst prediction
4.2 Case 2: Experimental results on classification
4.2.1 Datasets description
UCI [27] datasets are usually used to evaluate the performance of the algorithm. In this study, we chose eight benchmark datasets for testing, including binary and multiclass datasets, which are of relatively high or low dimensions, large or small sizes, and the details are summarized in Table 2.
Table 2 Datasets description

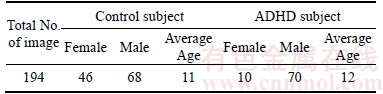
The fMRI data contain numerous spatiotemporal observations, which can reflect changes of functional networks in the brain. FMRI data are always used for investigating healthy brain function and detecting abnormalities. Attention deficit hyperactivity disorder (ADHD) is one of the most common diseases in young children. In this study, the fMRI dataset called “ADHD-200” is used for fMRI classification problem, which can be downloaded from the competition website [28]. The ADHD-200 data are time-series of 3D images of which size is 49*58*47. It consists of resting state fMRI data as well as different phenotypic information for each subject, including age, gender, verbal IQ, performance IQ, etc. There are several imaging sites: NeuroImage (NI), New York University Medical Center (NYU), Peking University (Peking), etc. We adopted the widely used ADHD-200 dataset provided by Peking University and the description is shown in Table 3.
Table 3 ADHD-200 dataset description
We preprocessed the ADHD-200 dataset using SPM8 toolbox [29], and chose 125 samples (68 controls, 57 ADHD) for this study. After feature extraction based on wavelet transform and reduction [30], the feature vectors are sent to the proposed GA-BEL for classification. By combining all ADHD subtypes in one category, the classification on ADHD-200 dataset is posed as a two-class classification, that is, ADHD’s subjects and normal controls.
4.2.2 Performance evaluation
Classification performance can be evaluated by the confusion matrix as described in Figure 7, in which measures such as accuracy, precision and recall are commonly used to assess the performance of bankruptcy classification systems. Among them, the classification accuracy (row 3-column 3, blue area) is the main evaluation index, which is calculated as follows [30, 31]:
 (22)
(22)
where TP is the number of true positives; TN is the number of true negatives; FP is the number of false positives; FN is the number of false negatives [30, 31]. Taking the classification on Breast Cancer dataset for example, the detailed explanations of TP, TN, FP and FN are given as follows:
TP: It means that some breast cancer cases (positives) are correctly classified as patients with breast cancer.
TN: It means that some healthy persons (negatives) are correctly classified as healthy persons.
FP: It means that some healthy persons are incorrectly classified as patients with breast cancer.
FN: It means that some cases with breast cancer are incorrectly classified as healthy persons.
The performance of execution speed can be evaluated by the computing time in training and testing process.

Figure 7 Confusion matrix
4.2.3 Classification results
1) Classification on Breast Cancer dataset
As mentioned above, the input patterns determine the number of neurons in Sensory cortex units, and the classes of samples determine the number of output units. Therefore, the learning parameters vary according to the samples. For the Breast Cancer dataset, parameters setting is separated for BEL and GA, as shown in Table 4. We used 70% of samples as training data, and the remaining 30% of samples were used to serve the validation and test purposes. The simulation results are shown in Figure 8.
Table 4 Parameters setting for GA-BEL algorithm (Breast Cancer dataset)

As shown in Figure 8(a), GA-BEL comes to convergence at iteration 100 where the value of mean fitness is nearly equal to the best fitness value, GA-BEL obtains the best chromosome. The confusion matrices in Figures 8(b, c) show the classification accuracies (row 3-column 3, blue area) are 96.1% and 97.6% in training and testing samples, respectively. The precision and recall are also given in the two confusion matrices. The whole process finished after 50 trials have been conducted, and finally the average results were recorded.
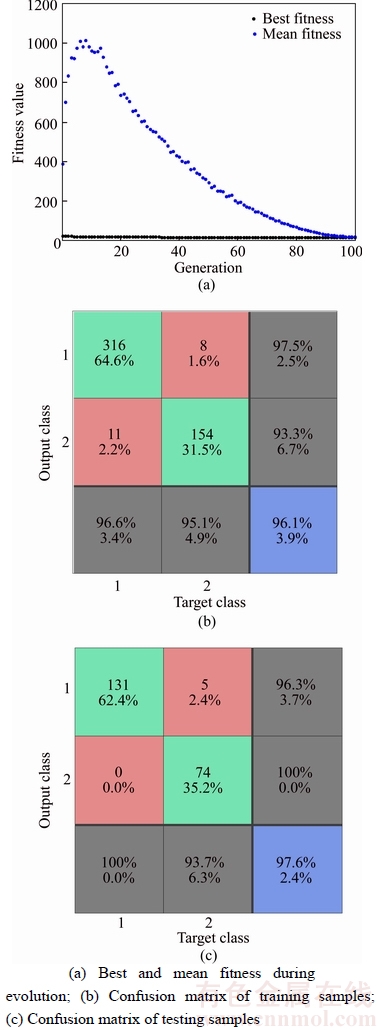
Figure 8 Classification results of GA-BEL (Breast Cancer dataset)
2) Classification on Heart dataset
To evaluate the GA-BEL on relatively small sizes and high dimensions dataset, we chose Heart dataset for test. Heart dataset has 270 samples with 13 features. According to the features of Heart dataset, the input nodes, hidden nodes and output nodes are respectively set to 13, 6, 2. We used 70% of samples as training data, while the rest is used to serve the validation and classification purposes. In GA, the population groups are set to 850 and each population size is set to 29, the crossover and the mutation rates are 0.7 and 0.03, respectively. To find the best value of the iteration number, different numbers of iterations from 100 to 900 were tried. Finally, GA-BEL achieves the best performance when the iteration number is equal to 700. Figures 9 and 10 show the results when the maximal generations are set to 500 and 700, respectively.
Compared with Figures 9(a) and 10(a), the best fitness value is improved. According to the confusion matrices in Figures 9(b, c) and 10(b, c), we can see that the GA-BEL achieves the testing accuracy (row 3-column 3, blue area) with 86.4% and 88.9% in 500 generations and 700 generations, respectively. We obtained the average accuracy and computing time after 50 trials have been conducted.
Next, GA-BEL was tested on Banana, Iris, SVMguide1, ADHD-200, etc. in turn. For each problem, 50 trials have been conducted, and finally the average accuracies were recorded, as well as the computing time.
4.2.4 Comparisons and discussions
The performance of GA-BEL is compared with SVM and the original BEL on the same datasets. The SVM is performed using the SVM toolbox [32] with Gaussian kernel. 50 trials have been conducted for each algorithm. The results in terms of average accuracy and computing time are recorded. Detailed comparison results are given in Table 5. For each dataset, the best accuracies and the shortest training time are highlighted.
As observed from Table 5, comparing to SVM, the BEL-based methods have the superior feature of fast training for they mimic the high speed of emotional processing in the emotional brain, and the computational complexity is low. While the training of SVM involves a quadratic programming problem, so the computational complexity is usually high. Thus, the execution speed is lower than BEL-based method. Although, SVM achieves higher accuracies in few cases.
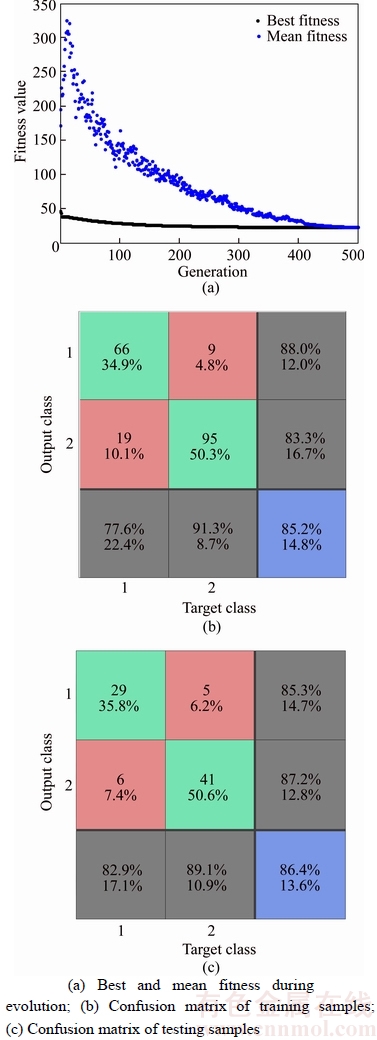
Figure 9 Classification results of GA-BEL (Heart dataset, 500 generations)

Figure 10 Classification results of GA-BEL (Heart dataset, 700 generations )
Compared with the original BEL algorithm, GA-BEL shows a significant improvement in terms of classification accuracy. GA-BEL employs GA to optimize the initial weights of amygdala and Orbitofrontal cortex in the BEL neural network, and the BEL network can be substantially improved after optimization. Thus GA-BEL is more accurate than BEL. Moreover, for the GA-BEL may encourage a grouping effect, it requires less training time for large size samples, so it is more efficient when dealing with large-scale classification problems.
For further comparison, we list the performance of the previous methods which investigated on the classification problem and seven datasets are specially chosen including high or low dimensions, large or small sizes. For each dataset, we report the testing accuracy and average computing time of each method. As shown in Table 6, GA-BEL achieves better classification accuracy and faster execution speed than the previous methods for most datasets.
5 Conclusions
An improved brain emotional learning algorithm (BEL) based on GA is proposed. The proposed GA-BEL algorithm mimics the high speed of emotional learning mechanism in the brain, which has the superior features of fast learning and low computational complexity. In addition, GA is applied to optimize the weights and biases of amygdala and orbitofrontal cortex in BEL neural network, which makes the BEL model more accurate.
A modified version of BEL neural network based on amygdala-orbitofrontal model is developed for prediction, as well as the extended architecture for classification. Instead of using reward-based reinforcement learning to adjust the learning rules, in this study, GA-BEL is employed to learn the pattern-target relationship of an application, it is model-free and can be generalized to classification, prediction and pattern recognition applications.
Two case studies were carried on benchmark prediction and classification problems, a chaotic time series of geomagnetic index for real-world prediction application, eight benchmark UCI datasets and a fMRI dataset for classification application. Results demonstrate the proposed GA- BEL achieves better generalization performance at faster execution speed compared to other algorithms for most datasets.
Table 5 Performance comparison of different algorithms

Table 6 Classification results obtained with proposed method and previous methods

This study introduces emotional intelligence into artificial intelligence, which opens a lot of research gates for the bio-inspired research. In future work, other optimization method can be employed, e.g., particle swarm optimization (PSO), which employs different strategies and computational effort to find a solution. Moreover, it is appropriate to combine GA with PSO to further improve the performance of the BEL network in the future investigation, and apply them in real-time applications.
References
[1] LARROZA A, MORATAL D, PAREDES-S NCHEZ A. Support vector machine classification of brain metastasis and radiation necrosis based on texture analysis in MRI [J]. Journal of Magnetic Resonance Imaging, 2015, 42(5): 1362–1368.
NCHEZ A. Support vector machine classification of brain metastasis and radiation necrosis based on texture analysis in MRI [J]. Journal of Magnetic Resonance Imaging, 2015, 42(5): 1362–1368.
[2] YAMASHITA Y, WAKAHARA T. Affine-transformation and 2D-projection invariant k-NN classification of handwritten characters via a new matching measure [J]. Pattern Recognition, 2016, 52(C): 459–470.
[3] SHI Tian, KONG Jian-yi, WANG Xing-dong, LIU Zhao, ZHENG Guo. Improved Sobel algorithm for defect detection of rail surfaces with enhanced efficiency and accuracy [J]. Journal of Central South University, 2016, 23(11): 2867–2875.
[4] KHOOBAN M H, JAVIDAN R. A novel control strategy for DVR: Optimal bi-objective structure emotional learning [J]. International Journal of Electrical Power & Energy Systems, 2016, 83: 259–269.
[5] SHARMA M K, KUMAR A. Performance comparison of brain emotional learning-based intelligent controller (BELBIC) and PI controller for continually stirred tank heater (CSTH) [J]. Lecture Notes in Electrical Engineering, 2015, 335: 293–301.
[6] MOR N J, BALKENIUS C. A computational model of emotional learning in the Amygdala [C]// Proceedings of the 6th International Conference on the Simulation of Adaptive Behaviour. MIT Press, 2000: 115–124.
N J, BALKENIUS C. A computational model of emotional learning in the Amygdala [C]// Proceedings of the 6th International Conference on the Simulation of Adaptive Behaviour. MIT Press, 2000: 115–124.
[7] LEDOUX J E. Emotion circuits in the brain [J]. Annual Review of Neuroscience, 2000, 23: 155–184.
[8] SHARAFI Y, SETAYESHI S, FALAHIAZAR A. An improved model of brain emotional learning algorithm based on interval knowledge [J]. Journal of Mathematics and Computer Science, 2015, 14: 42–53.
[9] LOTFI E. Wind power forecasting using emotional neural networks [C]// Proceedings of the IEEE International Conference on Systems, Man and Cybernetics. San Diego, USA: MIT Press, 2014: 311–316.
[10] SHARBAFI M A, LUCAS C, DANESHVAR R. Motion control of omni-directional three-wheel robots by brain- emotional-learning-based intelligent controller [J]. IEEE Transactions on Systems Man & Cybernetics Part C, 2010, 40(6): 630–638.
[11] LUCAS C, DANIAL S, NIMA S. Introducing Belbic: Brain emotional learning based intelligent controller [J]. Intelligent Automation & Soft Computing, 2004, 10(1): 11–21.
[12] ABDI J, MOSHIRI B, ABDULHAI B, SEDIGH A K. Forecasting of short-term traffic-flow based on improved neuro-fuzzy models via emotional temporal difference learning algorithm [J]. Engineering Applications of Artificial Intelligence, 2012, 25(5): 1022–1042.
[13] CHEN Jian-ping, WANG Jian-bin, YANG Yi-min. Velocity compensation control for a four-wheel drive robot based on brain emotional learning [J]. CAAI Transactions on Intelligent Systems, 2013, 8(4): 361–366.
[14] LOTFI E, AKBARZADEH T M R. Brain emotional learning-based pattern recognizer [J]. Cybernetics & Systems, 2013, 44(5): 402–421.
[15] CUI Lai-zhong, LI Geng-hui , LIN Qiu-zhen , DU Zhi-hua, GAO Wei-feng, CHEN Jian-yong, LU Nan. A novel artificial bee colony algorithm with depth-first search framework and elite-guided search equation [J]. Information Science, 2016 (367, 368): 1012–1044.
[16] CUI Lai-zhong, LI Geng-hui, LIN Qiu-zhen, CHEN Jian-yong, LU Nan. Adaptive differential evolution algorithm with novel mutation strategies in multiple sub-populations [J]. Computers & Operations Research, 2016, 67: 155–173.
[17] HOLLAND J H. Adaptation in Natural and Artificial Systems [M]. Cambridge, UK: MIT Press, 1992.
[18] DAS S, ABRAHAM A, KONAR A. Automatic clustering using an improved differential evolution algorithm [J]. IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2008, 38(1): 218–237.
[19] COOK D F, RAGSDALE C T, MAJOR R L. Combining a neural network with a genetic algorithm for process parameter optimization [J]. Engineering Applications of Artificial Intelligence, 2000, 13(4): 391–396.
[20] SHEN Z Q, KONG F S. Optimizing weights by genetic algorithm for neural network ensemble [J]. Lecture Notes in Computer Science, 2004, 3173: 323–331.
[21] WU Jian-shen, LONG Jin, LIU Ming-zhe. Evolving RBF neural networks for rainfall prediction using hybrid particle swarm optimization and genetic algorithm [J]. Neurocomputing, 2015, 148(2): 136–142.
[22] HOSSEINI Z, NAKHAE I M. Estimation of groundwater level using a hybrid genetic algorithm-neural network [J]. Pollution, 2015, 1(1): 9–21.
[23] LEDOUX J E. Emotion and the limbic system concept [J]. Concepts in Neuroscience, 1991, 2: 169–199.
[24] SRINIVAS M, PATTANAIK L M. Genetic algorithms: A survey [J]. Computer, 1994, 27(6): 17–27
[25] LOTFI E, AKBARZADEH-T M R. Adaptive brain emotional decayed learning for online prediction of geomagnetic activity indices [J]. Neurocomputing, 2014, 126(3): 188–196.
[26] HAGAN M T, DEMUTH H B, BEALE M. Neural network design [M]. Beijing: China Machine Press, 2002: 357.
[27] UCI machine learning repository [EB/OL]. [2017–03–02]. http://archive.ics. uci.edu/ml.
[28] ADHD-200 database. [2017–03–02]. http://fcon_1000.projects. nitrc.org/indi/adhd200/.
[29] SPM toolbox [2017–03–02]. http://www.fil.ion.ucl.ac.uk/ spm/.
[30] TAN Ying, ZHANG Tao, TAN Rui, SHEN Xiao-tao, XIAO Jing-zhong. Classification based Wavelet Translate and SVM in the ADHD [J]. Journal of University of Electronic Science and Technology of China, 2015, 44(5): 789–794.
[31] ZUO Wan-li, WANG Zhi-yan, LIU Tong, CHEN Hui-ting. Effective detection of Parkinson’s disease using an adaptive fuzzy k-nearest neighbor approach [J]. Biomedical Signal Processing & Control, 2013, 8(4): 364–373.
[32] LIBSVM: A library for support vector machines [EB/OL]. [2017–03-05]. http://www.csie.ntu.edu.tw/~cjlin/libsvm.
[33] ZHANG Zhao, ZHAO Ming-bo. Binary- and multi-class group sparse canonical correlation analysis for feature extraction and classification [J]. IEEE Transactions on Knowledge & Data Engineering, 2013, 25(10): 2192–2205.
[34] LUO Xiong, CHANG Xiao-hui, BAN Xiao-juan. Regression and classification using extreme learning machine based on L1-norm and L2-norm [J]. Neurocomputing, 2016, 174: 179–186.
[35] HUANG Guang-bin, ZHOU Hong-ming, DING Xiao-jian, ZHANG Rui. Extreme learning machine for regression and multiclass classification [J]. IEEE Transactions on Systems Man & Cybernetics: Part B, Cybernetics, 2012, 42(2): 513–529.
[36] BAI Zuo, HUANG Guang-Bin, WANG Dan-wei. Sparse extreme learning machine for classification [J]. IEEE Transactions on Cybernetics, 2014, 44(10): 1858–1870.
[37] RIAZ A, ALONSO E, SLABAUGH G. Phenotypic integrated framework for classification of ADHD using fMRI [C]// Proceedings of the 13th International Conference Image Analysis and Recognition. Springer International Publishing, 2016: 217–225.
(Edited by YANG Hua)
中文导读
基于改进大脑情感学习算法的有效数据分类
摘要:提出了采用遗传算法优化大脑情感学习模型的方法。大脑情感学习(BEL)模型是一种计算模型,由Morén等人于2000年根据神经生理学上的发现提出。该模型根据大脑中杏仁体和眶额皮质之间的情感学习机制建立,不完全地模拟了情感刺激在大脑反射通路中的信息处理过程。大脑情感学习模型具有结构简单、计算复杂度低、运算速度快的特点。为了进一步提高模型的精度,采用遗传算法优化调整大脑情感学习模型的权值,构造具有强泛化能力的大脑情感学习数据分析模型,并用于数据预测与数据分类两方面。在数据预测方面,采用典型的磁暴环电流指数Dst时间序列作为测试数据。实验结果表明,从均方差MSE和线性相关性R指标来看,GA-BEL算法的误差小、相关度高,说明该算法用于预测的有效性。在分类方面,采用8个典型的UCI数据集和一个典型的头部磁共振图像数据集(fMRI)作为测试数据。分类实验结果表明,GA-BEL算法的分类正确率高,运算速度快于传统算法,说明该算法用于分类的有效性。
关键词:预测;分类;大脑情感学习;遗传算法
Foundation item: Project(61403422) supported by the National Natural Science Foundation of China;Project(17C1084) supported by Hunan Education Department Science Foundation of China; Project(17ZD02) supported by Hunan University of Arts and Science, China
Received date: 2017-03-20; Accepted date: 2017-10-20
Corresponding author: TAN Guan-zheng, PhD, Professor; Tel: +86–13873646526; E-mail: 63641214@qq.com; ORCID: 0000-0003- 1237-7166

