Influence of melt superheat on breakup process of close-coupled gas atomization

OUYANG Hong-wu(欧阳鸿武), CHEN Xin(陈 欣), HUANG Bai-yun(黄伯云)

State Key Laboratory of Powder Metallurgy, Central South University, Changsha 410083, China

Received 13 October 2006; accepted 2 February 2007

Abstract: In close-coupled gas atomization(CCGA), the influences of melt superheat on breakup process are fundamental to obtain desired or finer powder. Based on a series of Cu atomization experiment under different superheating conditions, the influences of melt superheat on breakup process were studied. Experimental results indicate that as the melt superheat is increased to 150, 200, 250 and 300 K, the mean particle size (D₅₀) decreases consequently to 34.9, 32.3, 30.9 and 19.7 μm. Theoretical analysis reveals that the primary breakup and secondary breakup processes are close coupled, and the melt superheat radically influences the melt properties, and plays a crucial role on governing the filming process of primary breakup and the atomization modes of secondary breakup. There exists a strong nonlinear decrease of contact angle of melt to nozzle orifice wall when the superheat is increased from 250 K to 300 K, leading to a marked fall of the film thickness formed in primary breakup, and D₅₀ of copper powders is therefore sharply reduced. However, the log-normal distribution feature of particle size has not been substantially improved.

Key words: gas atomization; superheat; close-coupled nozzle; powder; particle size

1 Introduction

Close-coupled gas atomization(CCGA), with high fine powder productivity, high cooling rate and relatively lower gas consumption, is increasingly becoming the leading technology of manufacturing fine spherical metallic powders[1-3].

The main feature of CCGA is that there exists a unique gas recirculation zone below the nozzle, where interactions between melt and high pressure gas become so complex that it has not been understood well. How to optimize the operation parameters of CCGA is still an art more than a science. Despite of a wide range of application in modern powder processing technologies, the CCGA needs more control and enhancement to meet the demands of specific powder qualities for specific application, especially the particle size[4-6].

The melt superheat, one of the basic gas atomization parameters, is crucial to the powder particle size and distribution. However, it is hard to on-line observe the atomizing process and measure the continuous change of melt properties under high temperature and high speed gas flow within complex flow field structure, even the numerical methods cannot simulate the actual conditions as well. Thus, previous studies focused on this problem were all carried out by roughly correlating operation parameters and particle size while neglecting detailed atomization process, which only leads to individual and empirical results[7-12].

In this study, based on the experiment of atomizing copper melt under different superheats, an “inverse method”[13] was presented in term of the numerical mode of detailed breakup process to quantitatively analyze the influences of melt superheat on the particle size and distribution in CCGA.

2 Experimental

The experimental procedure was performed with a close-coupled atomizer. Commercial pure nitrogen was used as the atomizing gas. The gas resource consists of a band of twelve nitrogen gas cylinders manifold to a single two-stage high pressure gas regulator, with a maximum of 5 MPa. The experimental pressure was 3.5 MPa. The copper of 6 kg was atomized while being heated up to 1 506, 1 556, 1 606 and 1 656 K, respectively (the melting point of copper is 1 356 K,namely the superheat is 150, 200, 250 and 300 K), and the accuracy of temperature measurement was ±2 K. Each atomization process lasted about 90 s.

The morphology of atomized Cu powders was analyzed by scanning electron microscopy (SEM, Japan JEOL JSM-5600LV). The particle size distribution was measured with XRD (Micro-Plus LALLS).

3 Results

Fig.1 shows the SEM morphologies of copper powders under different superheats. All the four atomized powders show the similar feature, various in diameter, but all highly spherical. Furthermore, with gradual rise of melt superheat, the proportion of small particles (＜20 μm) increases whereas that of large particles (about 80 μm) decreases, as a result, the medium diameter falls. This trend becomes markable when the superheat is increased to 300 K.

Fig.1 SEM morphologies of Cu powders under different superheat: (a) 150 K; (b) 200 K; (c) 250 K; (d) 300 K

Fig.2 depicts the particle size distribution. All the four curves appear log-normal profiles, which is just the basic feature of close-coupled gas atomized powders. However, the curve of 300 K stands alone, where the particle size falls in a wide margin, which shows agreement with Fig.1. Fig.3 shows the medium diameters of copper powders under four different conditions. Apparently, it declines correspondingly with the rise of superheat. Firstly it declines at low pace (34.9, 32.3, and 30.9 μm, respectively), nevertheless, it plummets to 19.7 μm with a sharp fall by 36% at 300 K. So it is necessary to know why the powder particle sizes all appear the same log-normal distribution and what causes the sharp fall at the superheat of 300 K.

Fig.2 Particle size distribution under different superheating conditions

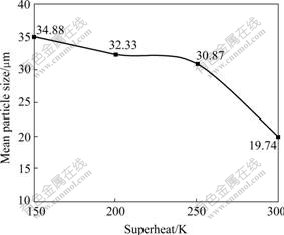
Fig.3 Mean particle size under different superheating conditions

4 Discussion

4.1 Schematic profile of gas velocity and melt tem- perature field of CCGA

The unique feature of CCGA is that there is a gas recirculation zone like a reverse cone downstream jet below the nozzle (orifice), as shown in Fig.4. The top of the cone is the gas stagnation point, where gas velocity goes to zero while pressure rises to maximum. The gas stream enters into the recirculation zone upstream via the stagnation front with a subsonic velocity. Near the melt orifice, the recirculating gas turns laterally (in radial direction) towards the circumferential edge. On reaching the edge, it encounters the sonic boundary, which forces the gas flow to turn downstream; consequently the recirculating gas is restricted within the cone, and separated from the outside supersonic flow. Thus, the gas velocity distribution within the atomization area is complex. Typically, the gas velocity and melt temperature fields along the central axis of close-coupled atomizer are illustrated in Fig.5[6]. On top of the diagram is the profile of temperature gradient of melt. The melt temperature approximately reduces in a step of 25 K per 6 mm accompanying with the liquid melt stream’s breakup, where T₀ is the initial temperature of the copper melt. In general, the cooling rate of melt droplet in CCGA is so high (about 10³-10⁸ K/s) that the whole disintegration process finishes in such a short period (nearly 10^-6 s)[14].

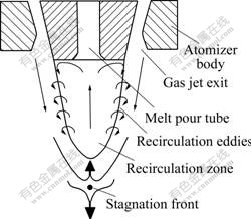
Fig.4 Schematic of gas recirculation zone

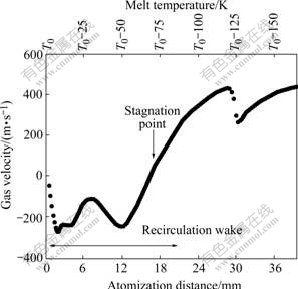
Fig.5 Profiles of gas velocity and melt temperature along central axis

4.2 Breakup process of melt in CCGA

Generally, the whole gas atomization goes through three closed coupled stages: primary breakup, secondary breakup and solidification. The primary breakup process undergoes three orderly steps: film growth, ligament and droplet formation, which are shown in Fig.6[15-17].

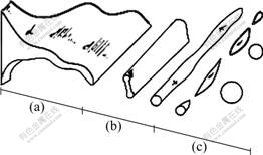
Fig.6 Primary breakup of liquid melt: (a) Film growth; (b) Ligament formation; (c) Droplets formation

a) In film growth step, firstly the liquid melt column exiting from the delivery tube runs into the recirculating gas zone; immediately the recirculating gas generates two opposite forces on melt column, where the stagnation pressure is upstream while the ambient suction is downstream. So those two forces are just like umbrella trestles, supporting the liquid column to be extruded into film, so called umbrella effect.

b) In ligament formation step, the liquid film under gas flow forms surface waves as a result of perturbation and instability, then it swells rapidly, so that it is torn into ligaments at half wave-length.

c) In droplet formation step, according to the Rayleigh instability, liquid ligament under high speed gas flow is dreadfully instable, so it develops instantly as short waves under the interaction of aerodynamic friction and surface tension. Furthermore given the shock-expansive wave’s oscillation, liquid ligaments are disintegrated into fine droplets in the end.

During the filming process, the thickness of film depends on the contact angle θ of the liquid to delivery tube orifice interface, and cannot be thinner than a minimum H_min (mm)[18]:

H_min=(1-cosθ)^0.22                             (1)

The diameter of ligament obtained from the tearing of continuous film is determined by the film thickness H and the maximum instable wave number K[19]:

;                        (2)

where  ρ_g is the gas density, U is the gas to melt flow velocity.

σ is the melt surface tension, which is a function of temperature T [20]:

σ=σ_m-k(T-T_m)                               (3)

where  σ_m is the melt’s surface tension at melting point T_m, k is a constant related to material’s property.

Obeying the Rayleigh instability, liquid ligament is broken into fine droplets. And the diameter of these droplets can be calculated with the following equation[19]:

d_p=1.88d_L(1+3Oh)^1/6                          (4)

where  d_p is diameter of droplet, Oh=μ_l/(ρ_lσd_L)^1/2, μ_l is viscosity of liquid droplet, ρ_l is density of liquid material. However, this breakup process is of randomness for the sake of Rayleigh instability itself, which leads to random distribution of droplet diameter.

As primary breakup is finished, liquid droplets immediately undergo the secondary breakup. During the secondary breakup, the droplet’s atomization conforms to the Weber number criterion:

We=ρ_gU²d_p/σ                                 (5)

Only those melt droplets whose Weber number reaches the critical value (generally considered to be 10.7) can be disintegrated further with a relevant mode as Twins, Bag, Film stripping and Catastrophic (according to Weber number)[21-23], which are illustrated in Fig.7. Combining Eqns.(1)-(5) and replacing superheat T-T_m with ΔT, while neglecting the influence of Oh number (too small) and considering that the fall of temperature during the primary breakup is about 50 K, we can get the equation as follows:

We=10.6U[ρ_g(1-cosθ)^0.22/σ_m-k(ΔT-50)]^0.5         (6)

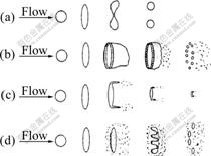
Fig.7 Droplets’ secondary breakup modes: (a) Twins, 10.7≤We≤12.0; (b) Bag, 12≤We≤100; (c) Film stripping, 100≤We≤350; (d) Catastropic, 350≤We

In different breakup modes, the melt droplets will undergo different deforming processes, as a result, powders finally gained are diversified in particle size and microstructure (droplet’s cooling rate depends on its diameter[24], and the final powder’s microstructure is determined by initial droplet’s cooling rate[25]). As regards to the Twins, the droplet diameter d_s can be computed by the equation below[21]:

                                (7)

For the Bag, the ring edge breaks into comparatively larger droplets, and the mean diameter is given as d_sr; while the hollow bag breaks into smaller droplets, with a mean diameter d_sb[26]:

d_sr=0.3d_p, d_sb=0.042d_p                          (8)

In the Film Stripping, droplet’s mean diameter can be represented by d_s as shown in the following equation [27]:

d_s=7.44d_p(ρ_l/ρ_g)^-0.25[μ_l/(ρ_ld_pU)]^0.5                (9)

Catastrophic breakup means a dramatic and complicated process that has not been understood well and can’t achieve in conventional conditions, but it is usually considered to produce ultra-fine and uniform powders. In fact, the final droplet’s diameter (after secondary breakup) decreases obviously as the Weber number rises. So we may safely draw a conclusion that in order to produce finer powders, one of the available ways is to get higher Weber number before secondary breakup.

According to Eqn.(6), there are four key factors influencing the Weber number, namely U, ρ_g, θ and σ, with the former two being positive, so all those methods of increasing U and ρ_g are effective to produce finer powders, such as optimizing nozzle design, increasing gas pressure, changing gas type and controlling melt flow rate. However, because of complicated gas recirculation zone below the melt exit and the uneven gas velocity distribution, the melt droplets in different position before secondary breakup will get different U, which leads to different Weber number and further undergo different secondary breakup modes. Besides, the breakup of this liquid melt sheet based on Rayleigh instability is random and the droplet diameters appear log-normal distribution. For this reason, close-coupled atomized powders are inevitably various in particle size, usually showing log-normal distribution.

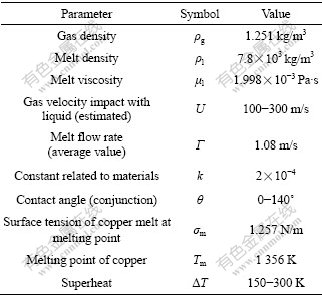
For θ and σ, they are both decreased with the rise of melt temperature, namely superheat here. Generally, the higher the melt superheat, the finer the particle size. The reason for the sharp fall of D₅₀ of atomized copper powders will be quantitatively analyzed in the following section. All related parameters are listed in Table 1.

Table 1 List of operation parameters

4.3 Influence of melt superheat on whole breakup process

Since operation parameters such as gas pressure, gas density, melt density and melt flow rate are fixed in the experiment, only the contact angle, surface tension and other variables in the breakup process need to be considered. As to the contact angle θ, it is completely different from that under the normal condition (static and without gas flow), and is therefore hard to measure or calculate. Besides, other variables’ influences are much easier to evaluate according to those equations mentioned above, θ is therefore probably the very factor causing the nonlinear change of D₅₀. Now we try to calculate it theoretically by using the so-called inverse method on the concrete basis of description of the detailed breakup process of melt, as well as the actual experimental results. Firstly, we should present a basic formulation to correlate θ and D₅₀. Given that there are probably one to four modes in secondary breakup, we thus impose θ an approximate value of 110?, without considering its decrease with the rise of superheat based on our recent works[16-17], and choose the immediate U of 200 m/s. Subsequently, the actual breakup mode is estimated according to Eqn.(6). The results are listed in Table 2.

Table 2 Estimation of secondary breakup mode

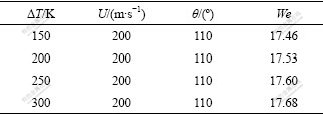
Obviously, the bag breakup mode should be dominant, so the basic formulation can be defined as follows:

d_s=C′(1-cosθ)^0.11[1.257-0.000 2(ΔT-50)]^0.5       (10)

where  C′ is a constant related to the breakup process, for the droplet obtained from the ring. C′ can be given as 0.014; as to the bag, C′ is 0.002[26].

In general, the droplets formed from the breakup of ring are much larger in diameter than that of hollow bag (In fact, most of the large particles in powders are originated from them), but much less in mass proportion. Moreover, they are still able to experience further breakup as the mode of twins, so here we only consider the breakup of bag. Based on Eqn.(10) and the experimental results of D₅₀, the appropriate value of θ under four superheats can be obtained with iterative adjustment. Since none of the above mentioned empirical equations could be used directly to approximate the given experiment, the best data fit could be achieved with necessary modification. Eqn.(10) can be transformed to the following from:

C″(1-cosθ)^0.11[1.257-2×10^-4(ΔT-50)]^0.5-D₅₀=0   (11)

where  C″ is a modified constant of 3.7×10^-5 relative to the present experiment; D₅₀ is the experimental results of mean particle size of copper powders. So the contact angle θ of melt to nozzle orifice wall can be approximately calculated as 60?, 45?, 35?, and 5? respectively, when superheat is gradually increased from 150 K to 300 K and the corresponding D₅₀ decreases nonlinearly from 34.9 μm to 19.7 μm.

Fig.8 illustrates the contact angle versus superheat temperature, which shows fair agreement to the profile of D₅₀ versus superheat. There is a dramatic decrease of contact angle when superheat is increased from 250 K to 300 K, which has been found by some investigations on the change of melt properties e.g. viscosity and surface tension with temperature[28]. The nonlinear change of melt properties with the rise of superheat temperature causes the dramatic decrease of contact angle, and the detailed mechanisms of this elusive physical chemistry phenomenon need further studies.

Fig.8 Contact angle versus superheat

Now we try to calculate the whole breakup process with the above estimated contact angle and modified Eqns.(1)-(9), so that we can correlate the nonlinear change of contact angle to the sharp fall of D₅₀. The calculation results are listed in Table 3.

Table 3 Calculation results of parameters in breakup process

Obviously, the higher the melt superheat, the thinner the film formed in primary breakup; the smaller the droplet formed in primary breakup, the finer the powder particle obtained in the end. Moreover, the bag breakup mode is dominative. They are both pretty accordant to the normal feature of CCGA.

When superheat is increased from 150 K to 250 K, the contact angle deceases slightly from 60? to 35?, so D₅₀ is reduced at low pace. Furthermore, the contact angle plunges into 5? with an 85.7% fall as superheat is increased to 300 K, which leads to the dramatic decrease of thickness of film formed in primary breakup from 0.686 mm to 0.294 mm. Therefore D₅₀ of powders is reduced sharply to 19.7 μm with a fall of 11.1 μm.

However, if the superheat is increased higherly, the Weber number of droplet will decrease below the critical value 10.7 and cannot break any more, so the powder particle size cannot be reduced further only by enhancing superheat much higher beyond normal range. Also, the evaporation of melt and durability of equipments are another limitation. In addition, the basic breakup mode of melt cannot be changed with the rise of superheat only. The primary breakup based on Rayleigh instability and secondary breakup of bag mode inevitably leads to the log-normal distribution.

  5 Conclusions

1) The melt superheat radically influences the melt properties, and therefore has crucial effects on the breakup process in CCGA. Generally, the higher the melt superheat, the smaller the contact angle; the thinner the melt film in primary breakup, which leads to finer powder particle size.

2) Experimental results indicate that as melt superheat is increased to 150, 200, 250 and 300 K, respectively, D₅₀ is decreased consequently to 34.9, 32.3, 30.9 and 19.7 μm. The analytical result reveals that there exists a dramatic nonlinear decrease of contact angle from 35? to 5? when superheat is dropped from 250 K to 300 K, which probably attributes to the radical change in melt properties. The inverse method used is demonstrated to be available to quantitatively analyze the detailed breakup process of CCGA.

3) The log-normal distribution of close-coupled atomized powders cannot be changed simply by increasing melt superheat, which is the instinct feature of CCGA. The mean particle size cannot be reduced further only by increasing superheat (due to the limitation of Weber number, melt evaporation and equipments durability) without the modification of nozzle design and other atomization parameters. Consequently, the whole operation parameters have to be adjusted synergy with the nonlinear feature of melt properties.

Appendix

List of symbols

H          Thickness of liquid film, m;

d          Diameter of liquid droplet, m;

Г          Flow rate of liquid melt, m/s;

K          Wave number;

U          Gas to melt velocity, m/s;

T          Melt temperature, K;

k          Constant related to melt properties;

ΔT          Melt superheat, K;

C          Modified coefficient.

Greek letters

θ          Contact angle, ?;

ρ          Density, kg/m³;

σ          Surface tension, N/m;

μ          Viscosity, Pa?s.

Subscripts

g          Corresponding to gas;

l          Corresponding to melt;

m          At melting point;

L          Ligament formed in primary breakup;

p          Droplets formed in primary breakup;

s          Droplets formed in secondary breakup;

min          Minimum;

max          Maximum.

References

[1] DOWSON A G. Atomization dominates powder production [J]. MPR, 1999, 54(1): 15-17.

[2] MILLER S A. Close-coupled gas atomization of metal alloy [C]// Proceedings ’PM’ 86. 1986: 29-32.

[3] MATES S P, SETTLES G S. High-speed imaging of liquid atomization by two different close-coupled nozzles [C]// CADLE T M, NARASIMHAN K S. Advances in Powder Metallurgy and Particulate Materials-1996. Princeton, NJ: MPIF, 1996: 67-80.

[4] TING J, ANDERSON I E. A computational fluid dynamics(CFD) investigation of the wake closure phenomenon [J]. Mater Sci Eng A, 2004, A379: 264-276.

[5] TING J, PERETTI M W, EISEN W B. The effect of wake-closure phenomenon on gas atomization performance [J]. Mater Sci Eng A, 2002, A326: 110-121.

[6] BEDDOW J K, HU Yun-xiu, CAO Yong-jia. The production of metal powders by atomization [M]. Beijing: Metallurgy Industry Press, 1985. (in Chinese)

[7] LAWLEY A. Atomization—The production of metal powders [M]. Princeton: Metal Powder Industries Federation, 1992.

[8] RAO P. Shape and other properties of gas atomized metal powders [D]. Philadelphia: Drexel University, 1973.

[9] STRAUSS J T, MILLER S A. Effect of melt superheat on powder characteristics produced by close-coupled gas atomization [C]// CADLE T M, NARASIMHAN K S. Advances in Powder Metallurgy and Particulate Materials-1996. Princeton, NJ: MPIF, 1996: 55-66.

[10] OZBILEN S, UNAL A, SHEPPARD T. Influence of superheat on particle shape and size of gas atomized copper powders [J]. Powder Metal, 1991, 34(1): 53-61.

[11] WOLF G, BERGMANN H. Investigations on melt atomization with gas and liquefied cryogenic gas [J]. Mater Sci Eng A, 2002, A326: 134-143.

[12] ANDERSON I E, TERPSTRA R L. Progress toward gas atomization processing with increased uniformity and control [J]. Mater Sci Eng A, 2002, A326: 101-109.

[13] BOHR T, PUTKARADZE V, WATANABE S. Averaging theory for the structure of hydraulic jumps and separation in laminar free-surface flows [J]. Physical Review Letters, 1997, 79(6): 1038-1041.

[14] LIU Y Z, CHEN Z H, WANG J N. Numerical simulation of the thermal history of droplets during multi-stage atomization [J]. Science and Technology of Advanced Materials, 2001, 2: 177-180.

[15] LI Q Q. The principle of powder production by the close-coupled gas atomization [J]. Powder Metallurgy Industry, 1999, 9(5): 3-16. (in Chinese)

[16] OUYANG Hong-wu, HUANG Bai-yun, CHEN Xin, YU Wen-tao, ZHANG Xin. Filming mechanism of high-pressure gas atomization in state of ‘opened’ wake [J]. The Chinese Journal of Nonferrous Metals, 2005, 15(7): 1000-1005. (in Chinese)

[17] OUYANG Hong-wu, HUANG Bai-yun, CHEN Xin, YU Wen-tao. Melt metal sheet breaking mechanism of close-coupled gas atomization [J]. Trans Nonferrous Met Soc China, 2005, 15(5): 985-992.

[18] EL-GENK M S, SABER H H. Minimum thickness of a flowing down liquid film on a vertical surface [J]. International Journal of Heat and Mass Transfer, 2001, 44: 2809-2825.

[19] SENECAL P K, SCHMIDT D P, NOUAR I, RUTLAND C J, REITZ R D, CORRADINI M L. Modeling high-speed viscous liquid sheet atomization [J]. International Journal of Multiphase Flow, 1999, 25: 1073-1097.

[20] MATSUMOTO T, FUJII H, UEDA T, KAMAL M, NOGL K. Measurement of surface tension of molten copper using the free-fall oscillating drop method [J]. Measurement Science and Technology, 2005, 16: 432-437.

[21] SHEIKHALI M, BERYUKHOV A V, DUNKLEY J J. Metal droplet’s deformation and break-up by a gas stream [C]// Shrewsbury. Powder Manufacturing and Processing. Vienna: European Powder Metallurgy Association, 2004: 1-6.

[22] LEE C H, REITZ R D. An experimental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream [J]. International Journal of Multiphase Flow, 2000, 26: 229-244.

[23] JOSEPH D. Breakup of a liquid drop suddenly exposed to a high-speed air stream [J]. International Journal of Multiphase Flow, 1999, 25: 1263-1303.

[24] BERGMANN D, FRITSCHING U, BAUCKHAGE K. A mathematical model for cooling and rapid solidification of molten metal droplets [J]. International Journal of Thermal Science, 2000, 39: 53-62.

[25] LEE E S, AHN S. Solidification progress and heat transfer analysis of gas-atomized alloy droplets during spray forming [J]. Acta Metal Mater, 1994, 9: 3231-3243.

[26] CHOU W H, FAETH G M. Temporal properties of secondary drop breakup in the bag breakup regime [J]. International Journal of Multiphase Flow, 1998, 24: 889-912.

[27] FAETH G M, HSIANG L. Structure and breakup properties of sprays [J]. International Journal of Multiphase Flow, 1995, 21: 99-127.

[28] TOMU T M, CHIRIAC H. Viscosity and surface tension of liquid Fe-metalloid glass-forming alloys [J]. Mater Sci Eng A, 2001, A304/306: 272-276.

Foundation item: Projects(10476043; 50574103) supported by National Natural Science Foundation of China

Corresponding author: OUYANG Hong-wu; Tel: +86-731-8877192; E-mail: oyhw1816@sina.com.cn

(Edited by HE Xue-feng)