J. Cent. South Univ. Technol. (2008) 15(s1): 187-191

DOI: 10.1007/s11771-008-343-x

Application in metal rheological forming of element-free Galerkin method

LUO Ying-she(罗迎社), YIN Shui-ping(殷水平)?，YU Min(余 敏)

(Institute of Rheological Mechanics and Material Engineering,

Central South University of Forestry and Technology, Changsha 410004, China)

Abstract: The element-free method is a new numerical technique presented in recent years. It uses the moving least square(MLS) approximation as its shape function, and it is determined by the basic function and weight function. The weight function is the mainly determining factor, so it greatly affects the accuracy of the computational results. The element-free Galerkin method(EFGM) was applied for the solution to plastic large deformation. The simulation of metal rheological forming was successfully done by programming and its results were visualized by using the plotting and data analyses software Tecplot. Then plastic strain under different stages during rheological forming and the three principal stresses at the last deformation were obtained. The example shows the feasibility of EFGM used for metal rheological forming and provides a new method for numerical simulation of rheological forming of complex parts.

Key words: element-free Galerkin method; weight function; rheological forming; numerical simulation

1 Introduction

At present, the finite element method(FEM) has become an important method for numerical calculation. However, some problems still exist in it. For example, the pre-processing has difficulties, and the results are usually discontinuous with stress and strain^[1-5], and the convergence problems caused by the distortion of grids are difficult and usually encountered in the larger deformation problems, such as high-speed impact analysis, the processing of metal forming, dynamic crack growth, solid-fluid coupled and the localization of strain and so on^[2]. The meshless method, whose basic idea is to remove the grids of finite element method completely, would be replaced with a series of nodes, using one treatment approximate to the related weight function indicating the characteristics information with weight function so as to get rid of grids.

Element-free Galerkin method(EFGM), which is one of the most developmental methods at present, has the advantages of high accuracy, steady solution and can eliminate volume atresia, and all these are relative closely to its weight functions.

In EFGM, the accuracy of calculation, efficiency, convergence and the steady of solution are influenced by different weight functions^[6-9]. Because the quartic spline weight function can keep a better accuracy and less consumptions in a larger support domain, the meshless Galerkin programming was designed to solve large deformation problems by quartic spline weight function, and the simulation of metal extrusion rheological forming was done by it, the result was visualized by data analysis software Tecplot, by which the three principle stress cloud diagram of final shape and plastic strain in different stages were obtained. Example shows the feasibility of metal rheological forming and provides a new way for volume forming.

2 Rheological forming of metal extrusion

Metal rheological forming technology is a metal processing method of less or without cutting, which plays an important role in the manufacture of metal parts. It not only has the advantages of high efficiency, high product quality and stability, and less material consumption, but also can effectively improve the organization of metal. Metal forming process is a complex physical process, which includes geometric non-linearity, physical non-linearity and contact non- linearity. The meshless method disperses the continuous body into finite particles and avoids the generation of grid, and provides a field function with a better continuity and flexibility, and it has tremendous advan-tages such as in dealing with large elastic-plastic deformation characteristics of the practical forming.

2.1 Constitutive theory

The large deformation of material in the metal process can use ratio form as expression in meshless Galerkin method of constitutive, and the stress and deformation can be described by Cauchy stress and strain ratio.

The strain vs displacement in geometry can be defined as

                            (1)

The relationship between the strain increment and the displacement increment is

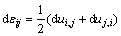                         (2)

Dividing Eqn.(2) with dt, the strain ratio vs velocity is obtained. Strain ratio is defined as the symmetry parts of velocity gradient.

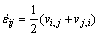                            (3)

The strain ratio can be determined by Eqn.(3) and the power of inner deformation of unit volume 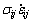 can also be obtained when the displacement velocity component of deformable body is given.

For the body with pre-stress, the Cauchy stress component changes as rotating, it does not equal zero, and cannot use in constitutive relationship as a non- objective-tensor. The objective ratio of considering rotation is used in the constitutive of large deformation rotation.

In this work, the Jaumann stress ratio is used, deviation Jaumann stress ratio is defined as

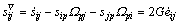                (4)

where  G is tangent modulus; Ω_ij is the rotation tensor component, and

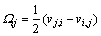                            (5)

Assume that the stress state is in elastic field when updating stress, there is

             (6)

where 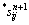  is proof stress. Define the valid proof stress as

                           (7)

If s* is larger than yield stress σ_s, then use Misses yield criterion

s_ijs_ij≤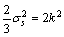                            (8)

and put proof stress to multiply a coefficient to yield surface,

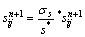                              (9)

2.2 Full Lagrange dispersion

Define the initial configuration as a reference configuration, the weak-form of Galerkin in nonlinear dynamics is

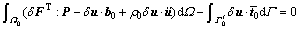 (10)

where  P is nominal stress tensor; b₀ is the body force of unit volume in domain Ω₀; 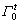 is the given surface force boundary in initial configuration;  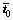is the given surface force load on  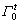and F is the deformation tensor of gradient. The motion equation of system is

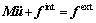                            (11)

Define the mass matrix M as

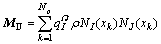                  (12)

The internal force vector matrix f ^int is

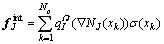                  (13)

The external force vector matrix f ^ext is

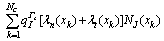             (14)

The description of stress increment in rheological forming is based on Eulerian coordinate. The derivative of stress with respect to time is relative to the velocity gradient of current configuration, and it can be transformed into the initial configuration by mixed derivation.

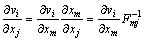                     (15)

The high non-linearity of material, physics and boundary condition exist in the process of rheological forming. The displayed time integral doesn’t require tangent stiffness matrix and doesn’t need to inverse tangent stiffness matrix, so it has a large advantage in analyzing metal rheological forming.

The particle shape function and its derivative which is described by Lagrange can be calculated only once, which avoids smooth particle hydrodynamics(SPH) method, searching at every step, the nodes in nodal influence domain to calculate shape function so as to improves efficiency.

2.3 Numerical example

Extrusion of metal rheological forming is a common technique. Take a cubical-shaped volume of 6 m sidelong as an example, and assume it was extruded into 1 m diameter cylindrical die. The simulation of metal extrusion rheological forming was done by programming (as shown in Fig.1), and the effect of friction was ignored.

Fig.1 Figure of metal extrusive rheological forming

In order to reduce the workload of calculation, in this work, by using 1/4 symmetrical model and dispersing in directions x, y and z by using the same nodes, the rheological forming above was done by meshless programming, the results obtained are as follows.

Fig.2 and Fig.3 show the change of coordinate on direction z of the center node (0, 0, 6) and corner node (3, 3, 6), because the center node generates displacement in z direction at beginning, following the metal block

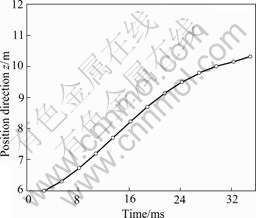
Fig.2 Position change in direction z of middle node (0, 0, 6) on top

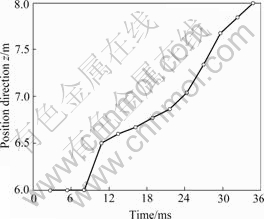
Fig.3 Position change in direction z of corner node (3, 3, 6) on top

squeezing into the upward, direction z enlarging continuously. However, the nodal displacement is zero in directions x and y as the node is in symmetric center (Fig.4). But for the corner node, the initial position is free in directions x and y and it is constrained in direction z, which generates displacement in direction z only it goes close to the entrance of extrusion. So the first part curve in Fig.3 is approximate level, and displacement in direction z would be generated until it goes close to the entrance of extrusion (the latter curve in Fig.5). The displacement is quite close in directions x and y in which, without restriction, the node is in symmetric surface of 1/8 (shown in Fig.5).

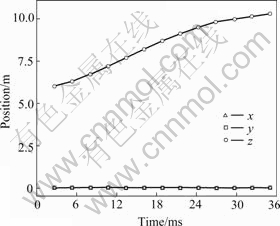
Fig.4 Position change at top of middle node (0, 0, 6)

3 Visual data processing

In the simulation of metal extrusion rheological forming, a great deal of node ASCII results were obtained from the program. But it is difficult to express by using data tables. So it is necessary to visualize the data to obtain an intuitive effects, such as stress and strain cloud, velocity vector and so on.

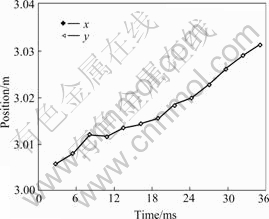
Fig.5 Position change at top of corner node (3, 3, 6)

As a powerful tool for data treating, Tecplot is widely used in engineering and scientific research, such as the aerospace, national defense, automotive, oil and other industries and fluid mechanics, heat transfer, earth science, and other researching fields. Therefore, this software will also be adopted in this work to visualize the numerical simulation results.

There are two kinds of data format in inputting into Tecplot, ASCII and binary format. An interface was programmed to import ASCII data format to Tecplot software.

Fig.6 shows the nodal plastic strain in different stages of rheological forming. Fig.7 shows the maximum plastic strain when the metal enters the cylindrical die.

Fig.6 Plastic strain under different stages during rheological forming: (a) 0.009 s; (b) 0.018 s; (c) 0.027 s; (d) 0.350 s

With the increase in the depth of extrusion, the material is gradually yielded, and the plastic strain increases as the increase in depth. Finally, the whole blank is in plastic state, which is consistent with the actual situation.

The first, second and third principal stresses were exported by the program, which were imported into the software of Tecplot. The cloud-figures for the first, second and third principal stresses at final shape, the plastic deformation are shown in Fig.7.

Fig.7 Three principal stresses at the last deformation: (a) The first principal stress; (b) The second principal stress; (c) The third principal stress

4 Conclusions

Based on the EFGM to solve large deformation of plastic problem, this paper achieves the process of metal extrusion simulation by programming; the example shows the feasibility on metal extrusion forming by using EFGM and provides a new idea for the numerical simulation of volume rheological forming, and a new calculating method for solving the problems of rheological forming. Meanwhile, the interface with Tecplot makes the data in calculation visualized and improves the data post-process efficiency.

However, the research on the meshless method is still in development and perfection, such as the rapid algorithm of it, implementing parallel algorithm and improving calculating efficiency in the basis of the existing achievement, its application on the simulation of complex shape parts in actual engineering under high-temperature rheological forming and so on, all these problems still need to study further.

References

[1] ZHOU Wei-yuan, KOU Xiao-dong. Element-free method and its application in engineering [J]. Acta Mechanica Sinica, 1998, 30(2): 193-202. (in Chinese)

[2] ZHANG Xiong, LIU Yan. Meshless method [M]. Beijing: Tsinghua Press, 2005: 1-2. (in Chinese)

[3] CHUNG H J, BELYTSCHKO T. An error estimate in the EFG method [J]. Computational Mechanics, 1998, 21: 91-100.

[4] BELYTSCHKO T, ORGAN D, KRONGAUZ Y. A coupled finite element-element-free Galerkin method [J]. Computational Mechanics, 1995, 17: 186-195.

[5] LONG Shu-yao, HU De-an. A study on the weight function of the moving least square approximation in the local boundary integral equation method [J]. Acta Mechanica Sinica, 2003, 16(3): 276-279.

[6] LIU G R, TU Z H. An adaptive procedure based on background cells for meshless methods [J]. Comput Methods Appl Mech Engrg, 2002, 191: 1923-1943.

[7] XIAO Q Z, DHANASEKAR M. Coupling of FE using collection approach [J]. Engineering Software, 2002, 33: 507-512.

[8] TIMOSHENKO S P, GOODIER J N. Theory of elasticity (3rd ed) [M]. New York: McGrawHill, 1987.

[9] YIN Shui-ping, LUO Ying-she, CAO Zheng, LIU Wen-bin. Study on weight functions efficiency of element-free Galerkin method [J]. National Science Journal of Xiangtan University, 2007, 29(3): 65-70. (in Chinese)

(Edited by CHEN Wei-ping)

Foundation item: Key project(02103) supported by National Education Department of China; Key project(02A008) supported by the Education Department of Hunan Province, China; Project(2005090) supported by Central South University of Forestry and Technology; Project(03JJY3007) supported by the Natural Science Foundation of Hunan Province, China; Project supported by the Rewarding Project for Excellent PhD Thesis of Hunan Province, China; Project(07031B) supported by Scientific Research Fund of Central South University of Forestry and Technology

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: YIN Shui-ping, Master; Tel: +86-731-5623021; E-mail: ysp8293@163.com