
J. Cent. South Univ. (2019) 26: 2543-2553
DOI: https://doi.org/10.1007/s11771-019-4193-5
Peristalsis of nanofluid through curved channel with Hall and Ohmic heating effects
T. HAYAT1, 2, B. AHMED1, F. M. ABBASI3, A. ALSAEDI2
1. Department of Mathematics, Quaid-I-Azam University, Islamabad 44000, Pakistan;
2. Nonlinear Analysis and Applied Mathematics (NAAM) Research Group, Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Comsats University Islamabad, Islamabad 44000, Pakistan
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: Nanofluids have attracted many scientists due to their remarkable thermophysical properties. Small percentage of nanoparticles when added to conventional fluid significantly enhances the heat transfer features. Sustainability and efficiency of nanomaterials have key role in the advancement of nanotechnology. This article analyzes the Hall, Ohmic heating and velocity slip effects on the peristalsis of nanofluid. Convective boundary conditions and heat generation/absorption are considered to facilitate the heat transfer characteristics. Governing equations for the peristaltic flow through a curved channel are derived in curvilinear coordinates. The equations are numerically solved under the assumption of long wavelength and small Reynold number. It has been observed that nanofluid enhances the heat transfer rate and reduces the fluid temperature. Hartman number and Hall parameter show reverse behavior in fluid motion and heat transfer characteristics. In the presence of velocity slip, the pressure gradient rapidly decreases and dominant effect is seen in narrow portion of channel.
Key words: peristalsis; nanofluid; Hall and Ohmic heating effects; convective boundary condition; velocity slip effects
Cite this article as: T. HAYAT, B. AHMED, F. M. ABBASI, A. ALSAEDI. Peristalsis of nanofluid through curved channel with Hall and Ohmic heating effects [J]. Journal of Central South University, 2019, 26(9): 2543-2553. DOI: https://doi.org/10.1007/s11771-019-4193-5.
1 Introduction
Novel idea of nanofluid gained attention because of its wide utility and applications. Due to the ability of enhancing thermal conductivity of ordinary fluids, different types of nanoparticles are used in nanofluids [1]. Some of these include metals (Al, Ag, Au, Cu, Fe), metal oxides (Al2O3, CuO), carbide ceramics (SiC, TiC), nitride ceramics (AlN, SiN), semiconductors (SiO2, TiO2) and carbon nanotubes [2]. Conventional base fluids are water, polymer solutions, transformer oil and ethylene glycol, etc. The rheological nature, cooling capacity and electrical characteristics of nanoparticles encouraged numerous scientists to use nanofluid in many engineering and biological fields. Further nanofluids are used to facilitate the heat transfer rate and modify the energy efficiency in thermal systems. Shape and size of nanoparticles play important role in describing the thermophysical nature of nanofluid. Some nuclear devices require high heat flux cooling therefore nanoparticles are used to attain required temperature. BRINKMAN [3] presented a mathematical model about viscosity of two phase fluid. DONG et al [4] have improved drag force model and discussed its application in simulating nanofluid flow. SEIKHOLESLAMI et al [5] investigated the convective heat transfer features of nanofluids in the presence of MHD. ALIABADI et al [6] experimentally examined the heat transfer features of fluid by considering different nanoparticles. They also analyzed that heat transfer enhancement of Cu-water nanofluid is comparatively higher than Fe-water and Ag-water nanofluid. FEIZABADI et al [7] presented the properties of nanofluid motion through twisted serpentine tube. He pointed out that an enhancement occurred in the efficiency of system upto 3.73 by adding Al2O3 nanoparticles in the ordinary liquid. XUAN et al [8] examined the inclusion of Cu-nanoparticles in water experimentally. The results depict that by adding nanoparticles in the ordinary liquid incredibly enhances the thermal efficiency of nanofluid. Some of the studies on the nanofluids can be seen through Refs. [9-20].
Phenomenon of peristalsis occurs due to the propagation of waves along the channel or tube walls. It is a well known mechanism of fluid transport in numerous industrial, physiological and biological systems. In human body the peristaltic transport is useful in the vasomotion of small blood vessels, urine transport from kidney to bladder, swallowing food via esophagus, movement of ovum in fallopian tube and in numerous reproductive mechanism. Further roller pump, finger pump, infusion pump and various industrial devices work through principle of peristaltic pumping. Modern medical devices like heart-lung machine are designed through this mechanism. Due to wide applications, numerous researchers have studied different aspects of peristaltic flow. HAYAT et al [21] examined peristaltic flow of nanofluid using different thermal conductivity models. ALI et al [22] discussed heat transfer analysis of peristaltic flow in curvilinear coordinates. ABBASI et al [23] numerically studied peristaltic flow of nanofluid with temperature dependent viscosity. Peristaltic transport of magneto nanofluid is important in the modern drug delivery process in which magnetic fluxes are applied to guide the nanoparticles towards target [24]. Addition of nanomaterial can be used to kill cancerous cells without affecting the nearby healthy cells by producing higher temperature around tumors. Further Hall effects are important in the study of peristaltic transport under the higher capacity of magnetic field. The
Hall parameter is the friction of electron cyclotron frequency and electron atom collision frequency. For strong magnetic field the Hall current is significant due to the Lorentz force and current density. ABBASI et al [25] studied the Hall and Ohmic heating effects on the peristaltic motion of nanofluid in a planar geometry. The combined effect of Hall current and applied magnetic field is very important in the magnetic resonance angiography. This process is used to generate images of arteries to evaluate these for stenosis (an abnormal narrowing in a blood vessel). This aspect of peristaltic motion in the presence of magnetic field and Hall parameter gain much attention. Convective boundary conditions explained the convective heat transfer between flowing fluid and surface. Heat transfer in several engineering and industrial processes like thermal energy storage, nuclear plant, gas turbine and material drying appropriately involve the convective boundary condition [26]. MAKINDE et al [27] examined flow of nanofluid with convective boundary conditions. Some studies examining peristaltic motion of nanofluid in the presence of Hall effects may include the works [28-33].
This study aims to investigate the Ohmic heating and Hall effects on the peristaltic transport of nanofluid in a curved channel. Further convective boundary and velocity slip conditions are considered. Corresponding equations and boundary conditions are simplified by using the small Reynolds number and large wavelength approximations. Dimensionless equations and boundary conditions are solved numerically. Effects of sundry parameters on velocity, pressure gradient and temperature have been depicted graphically.
2 Statement
Geometry of problem includes a two-dimensional curved channel with width 2a1 coiled in a semi circle of radius R′ and center O'. Coordinates of curved channel are represented in such a manner that 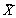 -axis is along the length of channel and
-axis is along the length of channel and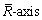 normal to
normal to An incompressible nanofluid is considered in the channel. Fluid flow is due to the propagation of waves along the channel walls with constant speed c, amplitude b and wavelength λ. Geometry of the waves is described as:
An incompressible nanofluid is considered in the channel. Fluid flow is due to the propagation of waves along the channel walls with constant speed c, amplitude b and wavelength λ. Geometry of the waves is described as:
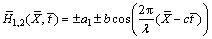 (1)
(1)
where t is the time,  and
and  depict the upper and lower walls. Constant temperature T0 and T1 (>T0) are maintained at
depict the upper and lower walls. Constant temperature T0 and T1 (>T0) are maintained at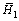 and
and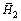 walls, respectively. Axial velocity for present flow is in the form
walls, respectively. Axial velocity for present flow is in the form 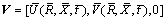 where
where  and
and 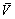 represent the radial and axial components of velocity. Further radial magnetic field is applied. It is taken in the form:
represent the radial and axial components of velocity. Further radial magnetic field is applied. It is taken in the form:
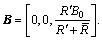
The Lorentz force is
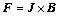 (2)
(2)
where current density in the presence of Hall current satisfies [25]:
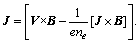
Finally Lorentz force becomes:
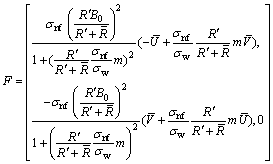 (3)
(3)
where σnf depicts the electrical conductivity of nanofluid, 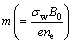 the Hall parameter, e is the electron charge, ne is the number density of free electron and σw is the electrical conductivity of water. Following Ref. [2] we have:
the Hall parameter, e is the electron charge, ne is the number density of free electron and σw is the electrical conductivity of water. Following Ref. [2] we have:
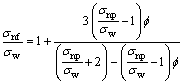 (4)
(4)
The Maxwell’s thermal conductivity (Knf) model of nanofluid is given as [12]:
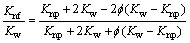 (5)
(5)
where subscript np represents the nanoparticles and w represents the base fluid for water and f stands for the nanoparticle volume fraction. Brinkman’s viscosity model for the two phase flow is given as [3]:
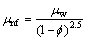 (6)
(6)
where μw is the viscosity of fluid. Viscosity of nanofluid increases along with the nanoparticle concentration. Mostly experimental results show that viscosity linearly enhances by increasing the nanoparticle concentration. The equations relevant to problem under consideration are [26, 28]:
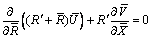 (7)
(7)
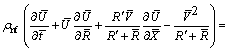
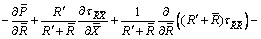
 (8)
(8)
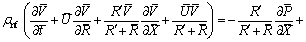
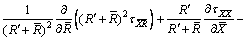
 (9)
(9)
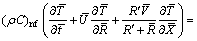

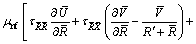
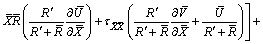
 (10)
(10)
where Φ denotes the dimensional heat generation/ absorption,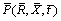 is the pressure, ρnf is the density of nanofluid and Cnf is the heat capacity of nanofluid. These quantities are taken into the following forms [2]:
is the pressure, ρnf is the density of nanofluid and Cnf is the heat capacity of nanofluid. These quantities are taken into the following forms [2]:
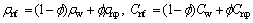 (11)
(11)
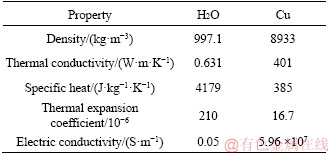
where subscripts w and np denote the water and nanoparticles phase. Numerical data of the thermophysical features of water and Cu nanoparticles are given through Table 1. The relations between the fixed and moving frames are described below:
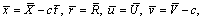
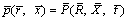 (12)
(12)
where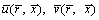 and
and are the axial velocity components and pressure in the moving frame. According to the above transformations, the relative equations of mass, momentum and energy are:
are the axial velocity components and pressure in the moving frame. According to the above transformations, the relative equations of mass, momentum and energy are:
 (13)
(13)
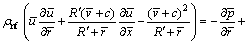
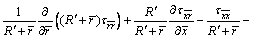
 (14)
(14)
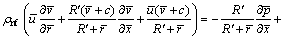

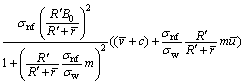 (15)
(15)
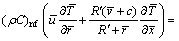
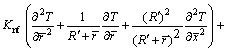


Table 1 Thermophysical properties [29] of water and Cu
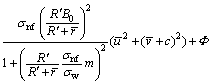 (16)
(16)
The non-dimensional forms of the above equations are presented in Appendix. Peristaltic transports are studied under the assumption of small Reynolds number and long wavelength. In light of these approximations, non-dimensional forms of Eqs. (14)-(16) are described by the expressions:

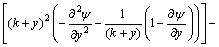
 (17)
(17)
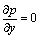 (18)
(18)
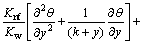

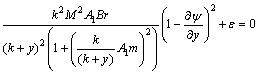 (19)
(19)
The non-dimensional parameters used in the above equations are [28]:


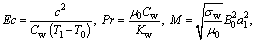
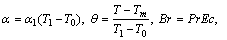
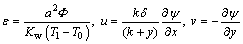 (20)
(20)
and continuity equation is trivially verified and Eq. (18) depicts that Here Pr, Ec, Br, Re, ψ, M, θ, δ, ε and Tm(=(T0+T1)/2) represent the Prandtl number, Eckert number, Brinkman number, Reynolds number, stream function, Hartman number, non-dimensional temperature, wave number, non-dimensional heat source/sink parameter and mean temperature of walls, respectively. Here
Here Pr, Ec, Br, Re, ψ, M, θ, δ, ε and Tm(=(T0+T1)/2) represent the Prandtl number, Eckert number, Brinkman number, Reynolds number, stream function, Hartman number, non-dimensional temperature, wave number, non-dimensional heat source/sink parameter and mean temperature of walls, respectively. Here
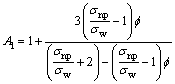 (21)
(21)
The non-dimensional flow rate in the fixed 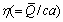 and moving
and moving 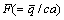 frames are associated with the relation [28]:
frames are associated with the relation [28]:
 (22)
(22)
Furthermore, F is given by:
 (23)
(23)
The convective boundary conditions [27] are described as below:
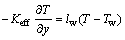 (24)
(24)
where lw represents the coefficient of heat transfer and Tw represents the temperature of the wall. Dimensionless velocity slip and convective boundary conditions are [2, 26]:
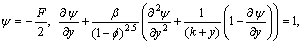

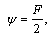
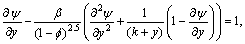
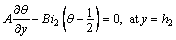 ;
;
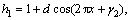
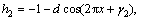
 (25)
(25)
where Bi1 and Bi2 are the Biot-numbers for the upper and lower walls and β represents the dimensionless velocity slip parameter. Here we use the Mathematica 9 software to compute the numerical solutions via NDSolve technique. This technique guarantees the accuracy in solution of the boundary value problem using suitable step size. In this problem, we choose step size 0.01 for the variation both in “x” and “y”. Next section presents the analysis of obtained results.
3 Discussion and comparison
In this section, we analyzed the numerical results through graphs and Tables. Effects of different parameters on velocity, pressure gradient and temperature are studied through graphs. Heat transfer rate is studied through table in detail. Discussion of physical quantities are provided separately below.
3.1 Velocity profile
Figure 1 shows the axial velocity for various values of nanoparticle volume fraction. There is a slight non-symmetry in graphs. It is due to curvature parameter. As expected, insertion of nanoparticles in base fluid decreases fluid velocity. Physically when inclusions of nanomaterial enhance in the base fluid then the effective viscosity of nanofluid is more and thus the ability of fluid motion reduces. Effect of Hall number on nanofluid is shown in Figure 2. Due to the presence of Hall parameter, the velocity rapidly increases compared with that in absence of Hall effects. It is noted that higher values of Hall parameter reduce the effective conductivity of nanomaterial therefore magnetic damping force decreases and consequently axial velocity increases. Figure 3 shows the magnetic field effect on velocity. As expected, the velocity decreases in presence of magnetic field due to the retarding nature of magnetic field. Figure 4 depicts the effect of β on the velocity profile. By increasing parameter β, velocity increases near the channel wall and it shows reverse behaviour near the center of channel. Figure 5 shows the variation of velocity by varying the curvature parameter. It can be seen that increasing behaviour shifted towards upper wall in view of consideration of curvature.

Figure 1 Effect of f on velocity when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, β=0.1, m=2.0, M=1.0 and k=3.0
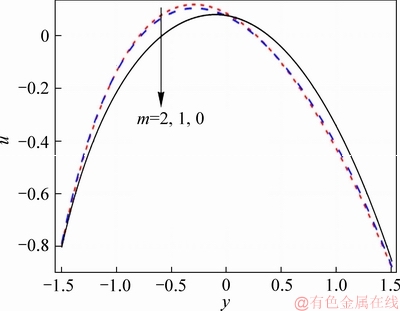
Figure 2 Effect of m on velocity when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, M=1.0 and k=3.0
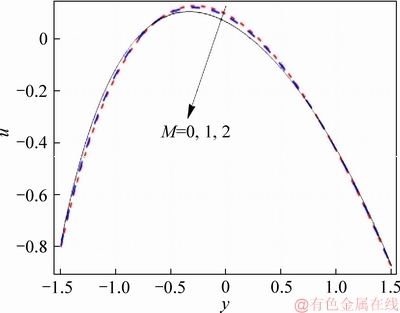
Figure 3 Effect of M on velocity when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, m=2.0 and k=3.0
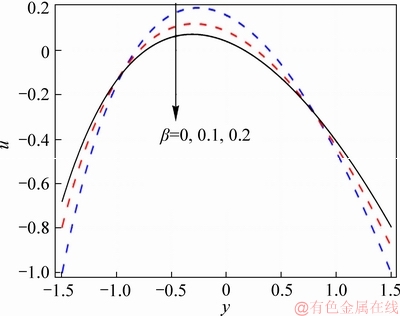
Figure 4 Effect of β on velocity when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, M=1.0, m=2.0 and k=3.0
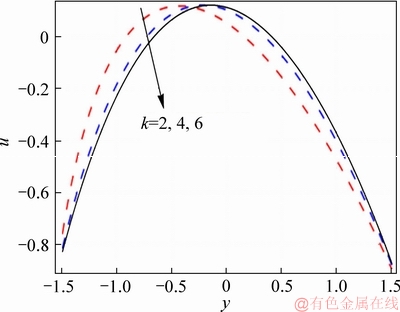
Figure 5 Effect of k on velocity when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, M=1.0, m=2.0 and k=3.0
3.2 Pressure gradient
Effects of numerous parameters on the pressure gradient are depicted through Figures 6-10. These graphs show sinusoidal behaviour of pressure gradient and attain higher value near the extensive portion of channel. Impact of f on pressure gradient is depicted in Figure 6. As nanoparticle volume fraction enhances, pressure gradient also increases. Inclusions of nanomaterial enhance the resistance of fluid motion therefore pressure gradient enhances. Figure 7 shows the influence of Hall parameter on the pressure gradient. Pressure gradient reduces with the rise of Hall parameter both in wider and occluded parts of channels. The impact of magnetic field on pressure gradient is shown in Figure 8. Pressure gradient enhances by an increase in strength of magnetic field. Figure 9 demonstrates the influence of β on pressure gradient. Pressure gradient decreases in presence of slip effects. The impact of curvature parameter on pressure gradient is shown in Figure 10. Pressure gradient slightly decreases by enhancing the curvature parameter.
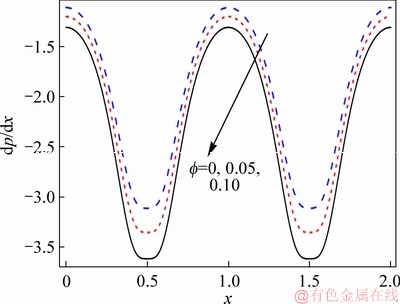
Figure 6 Effect of f on dp/dx when η=1.4, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, β=0.1, M=1.0, m=2.0 and k=3.0
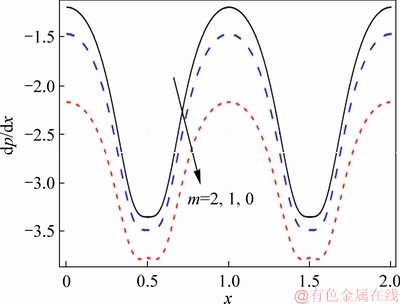
Figure 7 Effect of m on dp/dx when η=1.4, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, M=1.0 and k=3.0
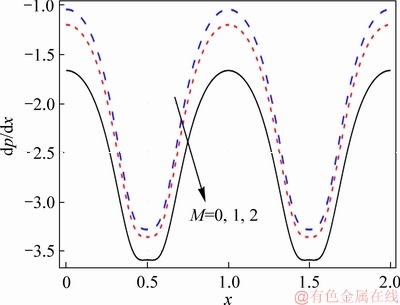
Figure 8 Effect of M on dp/dx when η=1.4, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, m=2.0 and k=3.0
3.3 Heat transfer analysis
Effect of f on the temperature of nanofluid is illustrated in Figure 11. As seen, temperature rapidly decreases by enhancing the nanoparticle volume fraction, due to the higher thermal conductivity of nanoparticles which tends to increase the heat transfer rate. Therefore, nanomaterial acts in industries as a coolant agent. Figure 12 exhibits the effect of Hall parameter on temperature. As depicted, temperature decreases in the presence of Hall parameter. Temperature decreases due to the effects of Hall parameter in Ohmic heating. Figure 13 depicts Hartman number effect on temperature. Temperature enhances for strong applied magnetic field due to Joule heating.Figures 14 and 15 indicate Biot number effect on the temperature at upper and lower channel walls. For larger Biot number, temperature rapidly decreases at both upper and lower walls. Temperature for values of curvature parameter is depicted in Figure 16. According to this Figure, temperature shows symmetric behaviour by increasing curvature parameter.
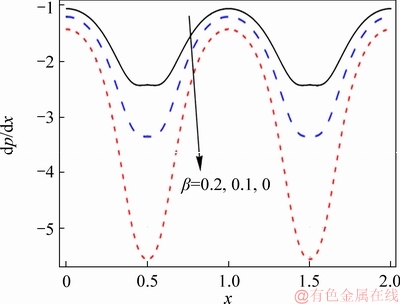
Figure 9 Effect of β on dp/dx when η=1.4, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, M=1.0, m=2.0 and k=3.0
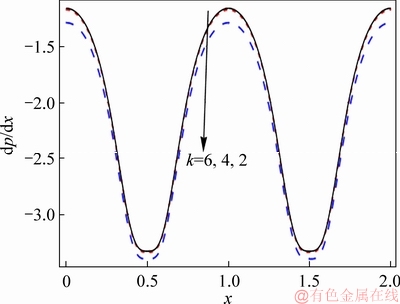
Figure 10 Effect of k on dp/dx when η=1.4, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, M=1.0, m=2.0 and β=0.1
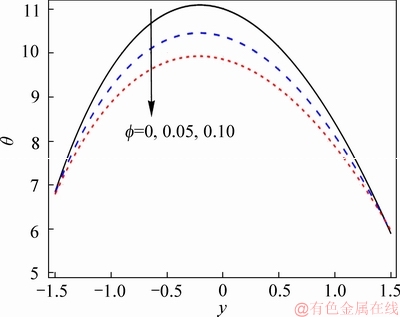
Figure 11 Effect of f on θ when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, Bi2=1.2, β=0.1, M=1.0, m=2.0 and k=3.0
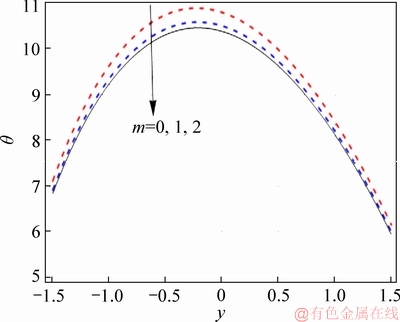
Figure 12 Effect of m on θ when η=1.4, x=1.0, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, Br=2.0, M=1.0 and k=3.0
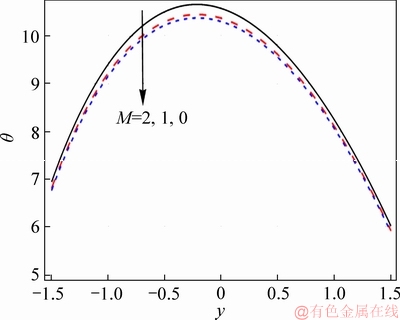
Figure 13 Effect of M on θ when η=1.4, x=1.0, ε=4.0, Bi1=0.9, Bi2=1.2, f=0.05, β=0.1, Br=0.2, m=2.0 and k=3.0
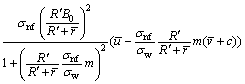
Heat transfer rate for various values of φ, m, M, Bi1, Bi2, Br, k and ε are shown in Table 2. According to this table, heat transfer rate increases by enhancing the nanoparticle volume fraction, Hartman number, Biot number, Brinkman number,curvature parameter and heat source/sink parameter. However, Hall parameter shows reverse behaviour. Inclusions of nanoparticles in conventional fluid enhance the heat transfer rate. It is due to the fact that nanoparticles have higher thermal conductivity. Larger values of Biot number facilitate the heat transfer characteristics and decrease the temperature of nanofluid. Behaviour of numerical data of heat transfer rate is qualitatively compared with the results of ABBASI et al [24]. The results show that heat transfer rate increases with higher volume fraction of nanomaterial and Hartman number. However, heat transfer rate decreases at the boundary for increasing value of Hall number. Further experimental results by XUAN et al [8] are qualitatively compared with the numerical data of the present work. Here the qualitative analysis indicates very good agreement.

Figure 14 Effect of Bi1 on θ when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi2=1.2, f=0.05, β=0.1, M=1.0, m=2.0 and k=3.0
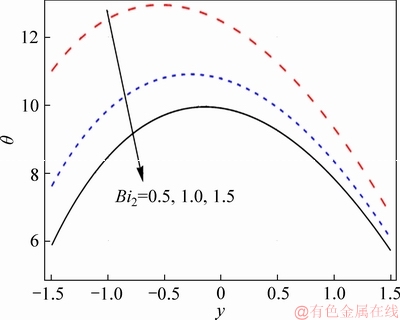
Figure 15 Effect of Bi2 on θ when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, f=0.05, β=0.1, M=1.0, m=2.0 and k=3.0
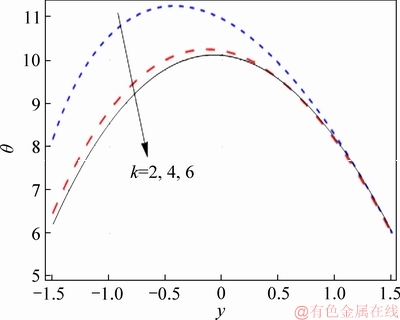
Figure 16 Effect of k on θ when η=1.4, x=1.0, Br=0.2, ε=4.0, Bi1=0.9, f=0.05, β=0.1, M=1.0, m=2.0 and Bi2=1.2
Table 2 Effects of f, m, M, Bi1, Bi2, Br, k and 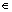 on heat transfer rate when η=1.4, β=0.1 and x=1.0
on heat transfer rate when η=1.4, β=0.1 and x=1.0

4 Conclusions
The main goal of this work is to provide a comprehensive analysis for peristaltic transport of nanofluid in a curved channel. The key findings are:
1) The inclusion of nanoparticles in base fluid improves the heat transfer rate and it decreases the temperature due to the higher thermal conductivity of nanomaterial;
2) Presence of nanoparticles in ordinary fluid decreases the axial velocity due to higher viscosity of material;
3) Heat transfer rate is improved in the presence of magnetic field. Hartman number rapidly decreases the temperature of nanofluid. Pressure gradient enhances with larger Hartman number;
4) In the presence of Hall effects, pressure gradient decreases. Further temperature and heat transfer rate also decrease;
5) Convective boundary condition improves the heat transfer characteristics and it decreases the fluid temperature rapidly;
6) Velocity increases near the wall by increasing velocity slip effects. However, opposite behaviour is noticed near the center of channel. Further velocity slip parameter enhances the pressure gradient.
Appendix
The non-dimensional forms of Eqs. (13)-(16) are [26, 28]:
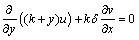 (A1)
(A1)
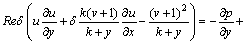
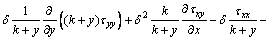
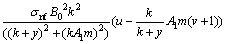 (A2)
(A2)
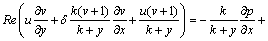

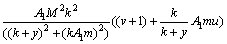 (A3)
(A3)
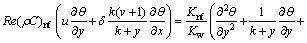



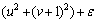 (A4)
(A4)
Further
 (A5)
(A5)
 (A6)
(A6)
 (A7)
(A7)
 (A8)
(A8)
References
[1] CHOI S U S. Enhancing thermal conductivity of fluids with nanoparticles [J]. ASME Fluids Eng Div, 1995, 231: 99-105.
[2] HAYAT T, AHMED B A, ABBASI F M, ALSAEDI A. Hydromagnetic peristalsis of water based nanofluids with temperature dependent viscosity: A comparative study [J]. Journal of Molecular Liquids, 2017, 234: 324-329.
[3] BRINKMAN H C. The viscosity of concentrated suspensions and solutions [J]. J Chem Phys, 1952, 20: 571-581.
[4] DONG S, ZHENG L, ZHANG X, LIN P. Improved drag force model and its application in simulating nanofluid flow [J]. Microfluid Nanofluid, 2014, 17: 253-261.
[5] SHEIKHOLESLAMIA M, ELLAHI R, VAFAI K. Study of Fe3O4-water nanofluid with convective heat transfer in the presence of magnetic source [J]. Alexandria Engineering Journal, 2018, 57: 565-575.
[6] ALIABADI M K, PAZDAR S, SARTIPZADEH O. Experimental investigation of water based nanofluid containing copper nanoparticles across helical microtubes [J]. International Communications in Heat and Mass Transfer, 2016, 70: 84-92.
[7] FEIZABADI A, ALIABADI M K, RAHIMI A B. Numerical investigation on Al2O3/water nanofluid flow through twisted-serpentine tube with empirical validation [J]. Applied Thermal Engineering, 2018, 137: 296-309.
[8] XUAN Yi-min, LI Qiang. Heat transfer enhancement of nanofuids [J]. International Journal of Heat and Fluid Flow 2000, 21: 58-64.
[9] ALIABADI M K, ALIZADEH A. An experimental study of Cu–water nanofluid flow inside serpentine tubes with variable straight-section lengths [J]. Experimental Thermal and Fluid Science, 2015, 61: 1-11.
[10] ALIABADI M K, RADB S E H, HORMOZI F. Al2O3–water nanofluid inside wavy mini-channel with different cross-sections [J]. Journal of the Taiwan Institute of Chemical Engineers, 2016, 58: 8-18.
[11] ALIABADI M K, NOURI M, SARTIPZADEH O, SALAMI M. Performance of agitated serpentine heat exchanger using metallic nanofluids [J]. Chemical Engineering Research and Design, 2016, 109: 53-64.
[12] MAXWELL J C. A treatise on electricity and magnetism [M]. 2nd Edition. Cambridge: Oxford University Press, 1904: 435-441.
[13] SHEHZAD S A, TARIQ HUSSAIN, HAYAT T, RAMZAN M, ALSAEDI A. Boundary layer flow of third grade nanofluid with Newtonian heating and viscous dissipation [J]. Journal of Central South University, 2015, 22(1): 360-367.
[14] ur REHMAN K, MALIK A A, TAHIR M, MALIK M Y. Undersized description on motile gyrotactic micro-organisms individualities in MHD stratified water-based Newtonian nanofluid [J]. Results in Physics, 2018, 8: 981–987.
[15] ZHANG C, ZHENG L, ZHANG X, CHEN G. MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction [J]. Applied Mathematical Modelling, 2015, 39: 165-181.
[16] ELLAHI R, HASSAN M, ZEESHAN A. Shape effects of nanosize particles in Cu-H2O nanofluid on entropy generation [J]. International Journal Heat and Mass Transfer, 2015, 81: 449-456.
[17] SHEIKHOLESLAMI M, HAYAT T, ALSAEDI A. Numerical simulation of nanofluid forced convection heat transfer improvement in existence of magnetic field using lattice Boltzmann method [J]. Int J Heat and Mass Transfer, 2017, 108: 1870-1883.
[18] ul HAQ R, NADEEM S, KHAN Z H, NOOR N F M. MHD squeezed flow of water functionalized metallic nanoparticles over a sensor surface [J]. Physica E: Low-dimensional Systems and Nanostructures, 2015, 73: 45-53.
[19] HAYAT T, AZIZ A, MUHAMMAD T, AHMAD B. Influence of magnetic field in three-dimensional flow of couple stress nanofluid over a nonlinearly stretching surface with convective condition [J]. PloS One, 2015, 10: e0145332.
[20] HAYAT T, AZIZ A, MUHAMMAD T, ALSAEDI A. On model for flow of Burgers nanofluid with Cattaneo-Christov double diffusion [J]. Chinese Journal of Physics, 2017, 55: 916-929.
[21] HAYAT T, BILAL A, ABBASI F M, AHMAD B. Mixed convective peristaltic flow of carbon nanotubes submerged in water using different thermal conductivity models [J]. Computer Methods and Programs in Biomedicine, 2016, 135: 141-150.
[22] ALI N, SAJID M, JAVED T, ABBAS Z. Heat transfer analysis of peristaltic flow in a curved channel [J]. International Journal of Heat and Mass Transfer, 2017, 53: 3319-3325.
[23] ABBASI F M, HAYAT T, SHEHZAD S A, ALSAADI F, ALTOAIBI N. Hydromagnetic peristaltic transport of copper-water nanofluid with temperature-dependent effective viscosity [J]. Particuology, 2016, 27: 133-140.
[24] ABBASI F M, HAYAT T, ALSAEDI A. Peristaltic transport of magneto-nanoparticles submerged in water: Model for drug delivery system [J]. Physica E, 2015, 68: 123-132.
[25] ABBASI F M, HAYAT T, AHMAD B. Peristalsis of silver- water nanofluid in the presence of Hall and Ohmic heating effects: Applications in drug delivery [J]. J Mol Liq, 2015, 207: 248-255.
[26] HAYAT T, AHMED B, ABBASI F M, ALSAEDI A. Flow of carbon nanotubes submerged in water through a channel with wavy walls with convective boundary conditions [J]. Colloid Polymer Science, 2017, 295: 1905-1914.
[27] MAKINDE O D, AZIZ A. Boundary layer flow of a nanofluid past a stretching sheet with a convective boundary condition [J]. International Journal of Thermal Sciences, 2011, 50: 1326-1332.
[28] SHEHZAD S A, ABBASI F M, HAYAT T, ALSAADI F, MOUSA G. Peristalsis in a curved channel with slip condition and radial magnetic field [J]. International Journal of Heat and Mass Transfer, 2015, 91: 562-569.
[29] TANVEER A, HAYAT T, ALSAEDI A, AHMAD B. On modified Darcy's law utilization in peristalsis of Sisko fluid [J]. J Mol Liquids, 2017, 236: 290-297.
[30] TANVEER A, HAYAT T, ALSAADI F, ALSAEDI A. Mixed convection peristaltic flow of Eyring-Powell nanofluid in a curved channel with compliant walls [J]. Computers in Biology and Medicine, 2017, 82: 71-79.
[31] ALI N, JAVID K, SAJID M, ZAMAN A, HAYAT T. Numerical simulation of Oldroyd 8-constant fluid flow and heat transfer in a curved channel [J]. International Journal of Heat and Mass Transfer, 2016, 94: 500-508.
[32] HINA S, MUSTAFA M, HAYAT T, ALSAEDI A. Peristaltic transport of Powell-Eyring fluid in a curved channel with heat/mass transfer and wall properties [J]. International Journal of Heat and Mass Transfer, 2016, 101: 156-165.
[33] HAYAT T, FAROOQ S, ALSAEDI A. Mixed convection peristaltic motion of copper-water nanomaterial with velocity slip effects in a curved channel [J]. Computer Methods and Programs in Biomedicine, 2017, 142: 117-128.
(Edited by FANG Jing-hua)
中文导读
霍尔效应和欧姆热效应下纳米流体通过弯曲通道时的蠕动
摘要:纳米流体以其优异的热物理性质吸引了许多科学家。在常规流体中加入少量的纳米粒子会显著地增强传热特性。纳米材料的可持续性和效率对纳米技术的进步具有关键作用。本文分析了霍尔效应、欧姆热效应和速度滑移对纳米流体蠕动的影响。考虑了对流边界条件和热的产生/吸收,以促进传热特性。在曲线坐标下导出了弯曲通道中蠕动的控制方程。在长波长和小雷诺数的假设条件下,对方程进行了数值求解。研究表明,纳米流体提高了传热速率,降低了流体温度。Hartman数和Hall参数在流体运动和传热特性上表现出相反的行为。在存在速度滑移的情况下,压力梯度迅速减小,在通道的狭小区域表现出主导作用。
关键词:蠕动;纳米流体;霍尔效应和欧姆热效应;对流边界条件;速度滑移效应
Received date: 2018-04-03; Accepted date: 2018-12-17
Corresponding author: F. M. ABBASI, PhD, Assistant Professor; Tel: +92-3444995951; E-mail: abbasisarkar@gmail.com; ORCID: 0000-0002-4214-3929