An attribute recognition model for safe thickness assessment between concealed karst cave and tunnel
来源期刊:中南大学学报(英文版)2019年第4期
论文作者:许振浩 张波 黄鑫 LI Shu-cai(李术才) 郭明 施雪松 高斌 刘浪
文章页码:955 - 969
Key words:concealed karst cave; karst tunnel; safe thickness; attribute recognition method
Abstract: An attribute recognition model for safe thickness assessment between a concealed karst cave and a tunnel is established based on the attribute mathematic theory. The model can be applied to carrying out risk classification of the safe thickness between a concealed karst cave and a tunnel and to guarantee construction’s safety in tunnel engineering. Firstly, the assessment indicators and classification standard of safe thickness between a concealed karst cave and a tunnel are studied based on the perturbation method. Then some attribute measurement functions are constructed to compute the attribute measurement of each single index and synthetic attribute measurement. Finally, the identification and classification of risk assessment of safe thickness between a concealed karst cave and a tunnel are recognized by the confidence criterion. The results of two engineering application show that the evaluation results agree well with the site situations in construction. The results provide a good guidance for the tunnel construction.
Cite this article as: HUANG Xin, LI Shu-cai, XU Zhen-hao, GUO Ming, SHI Xue-song, GAO Bin, ZHANG Bo, LIU Lang. An attribute recognition model for safe thickness assessment between concealed karst cave and tunnel [J]. Journal of Central South University, 2019, 26(4): 955–969. DOI: https://doi.org/10.1007/s11771-019-4063-1.

J. Cent. South Univ. (2019) 26: 955-969
DOI: https://doi.org/10.1007/s11771-019-4063-1

HUANG Xin(黄鑫)1, LI Shu-cai(李术才)1, XU Zhen-hao(许振浩)1, 2, 3, GUO Ming(郭明)1, 4,
SHI Xue-song(施雪松)2, GAO Bin(高斌)2, ZHANG Bo(张波)5, LIU Lang(刘浪)6
1. Geotechnical & Structural Engineering Research Center, Shandong University, Ji’nan 250061, China;
2. School of Qilu Transportation, Shandong University, Ji’nan 250061, China;
3. SinoProbe Center-China Deep Exploration Center,Chinese Academy of Geological Sciences,Beijing 100037, China;
4. China Railway Engineering Consulting Group Co., Ltd., Zhengzhou 450001, China;
5. School of Civil Engineering, Shangdong University, Ji’nan 250061, China;
6. School of Energy, Xi’an University of Science and Technology, Xi’an 710054, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2019
Abstract: An attribute recognition model for safe thickness assessment between a concealed karst cave and a tunnel is established based on the attribute mathematic theory. The model can be applied to carrying out risk classification of the safe thickness between a concealed karst cave and a tunnel and to guarantee construction’s safety in tunnel engineering. Firstly, the assessment indicators and classification standard of safe thickness between a concealed karst cave and a tunnel are studied based on the perturbation method. Then some attribute measurement functions are constructed to compute the attribute measurement of each single index and synthetic attribute measurement. Finally, the identification and classification of risk assessment of safe thickness between a concealed karst cave and a tunnel are recognized by the confidence criterion. The results of two engineering application show that the evaluation results agree well with the site situations in construction. The results provide a good guidance for the tunnel construction.
Key words: concealed karst cave; karst tunnel; safe thickness; attribute recognition method
Cite this article as: HUANG Xin, LI Shu-cai, XU Zhen-hao, GUO Ming, SHI Xue-song, GAO Bin, ZHANG Bo, LIU Lang. An attribute recognition model for safe thickness assessment between concealed karst cave and tunnel [J]. Journal of Central South University, 2019, 26(4): 955–969. DOI: https://doi.org/10.1007/s11771-019-4063-1.
1 Introduction
With the rapid development of transportation industry in China, the proportion of mountain tunnel construction in karst regions is also increasing year by year, and many challenges are faced in tunnel projects [1–6]. The concealed karst cave, a special unfavorable geology, directly threatens the normal construction and later safety operation of mountain tunnels [7–9]. The key to solving this problem is to determine the safe thickness between a concealed karst cave and a karst tunnel [10–13]. Therefore, the excavation can be stopped in time before the distance between tunnel face and the karst cave is less than the safe thickness during construction; finally, several measures can be taken to treat the concealed karst cave to prevent major karst disasters, such as water and mud inrush [14]. SONG et al [15] thought that the influence of concealed karst caves on karst tunnel is the fundamental scientific problems faced by the stability evaluation of surrounding rock. And the minimum safe thickness between a karst tunnel and a large cave on the top was derived by the elastic theory.
However, the predecessors studied the influence factors of concealed karst caves on the safe thickness just from a single aspect. Research on comprehensive analysis of all influential factors of safe thickness is rare.
Based on the attribute mathematics theory, an attribute recognition model is established for the evaluation of the safe thickness between a concealed cave and a karst tunnel. The plastic zone radius of an oval tunnel is solved through the perturbation method. Corresponding assessment indices and controlling measures are selected to deal with water-filled karst caves. This is of practical significance for the investigation, design and construction of deep-buried long tunnels as more and more tunnels are constructed in karst areas.
2 Attribute recognition system for evaluation of safe thickness between a concealed karst cave and a tunnel
The evaluation of safe thickness between a concealed cave and a tunnel is a comprehensive system. The input of the system is the measured values of m indices of a concealed karst cave, and the output of the system is the identification and estimation of a certain evaluation category, namely, the tunnel surrounding rock stability. The system can be divided into three subsystems, i.e., single index attribute measure analysis, multiple indices synthetic attribute measure analysis and attribute recognition analysis [16–18].
Set X as a set of a karst tunnel, known as the assessment object space. And its evaluation objects xi (i=1, 2, …, n) having m indices to be evaluated, i.e., Ij (j=1, 2, …, m); for the jth index Ij of xi, its measured value is tj, which has p evaluation levels, i.e., Ck (k=1, 2, …, p). Set F={safe thickness levels of a concealed karst cave towards tunnel stratum}, known as the attribute space. And every situation in the attribute space F is called an attribute set. For example, it can be specified that C1={level I}, C2= {level II}, C3={level III}, and C4={level IV} which stand for “safety”, “basic safety”, “dangerous” and “extremely dangerous” respectively. They are all a state of the stability of tunnel surrounding rock, belonging to the attribute set as well as the subset of F. Attribute calculation can be performed for the attribute set. Different attribute sets can produce corresponding attribute measure, which can satisfy the additive rule. The measured value tj of the jth evaluation index of evaluation object has the magnitude of attribute Ck, and is expressed by single index attribute measure μxjk. When evaluation object possesses the magnitude of level Ck, it is expressed by synthetic attribute measure μxk [19–21].
2.1 Single index attribute measure analysis
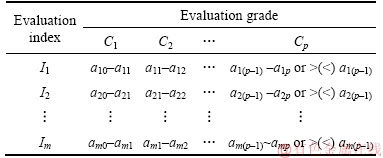
In the evaluation object space X of identification or estimation of the tunnel surrounding rock stability, the evaluation of safe distance between the concealed cave and the tunnel needs to measure every single index in the karst tunnel, such as surrounding rock grade, water pressure in the karst cave, shape of the karst cave, size of the karst cave, attitude of rocks, lateral pressure coefficient of rock mass, tunnel buried depth, and relative position of a karst cave and a tunnel, which are expressed by Ij (j=1, 2, …, m). The evaluation set in X is (C1, C2, …, Ck), and Ck (1≤k≤p) stands for the level of safe thickness, and the measured value of every index is given in the numerical form. Every karst tunnel to be evaluated can be expressed by a m-dimension variable, i.e., x=(t1, t2, …, tm). The measured value tj of the jth index of a karst tunnel possesses the magnitude of attribute Ck, and is measured by single index attribute measure μxjk. The safe thickness with the magnitude of level Ck is expressed by synthetic attribute measure μxk. The evaluation of tunnel surrounding rock stability is the evaluation of karst tunnel with m index values. For the measured value tj of single index Ij, the determination method of attribute measure μxjk=μ (xij∈Ck) (1≤k≤p) with attribute Ck is through building up its measure function of attribute, which can express the variation of attribute measure μxjk=μ (xij∈Ck) (1≤k≤p) when the measured value tj of Ij changes. The attribute measure function [20, 21] is built based on Table 1.
In Table 1, ajk satisfies aj0
Table 1 Grade subdivision of single index
There are two important parameters (bjk and djk) for constructing the attribute measure functions. Let
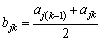 , k=1, 2, …, p (1)
, k=1, 2, …, p (1)
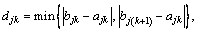 k=1, 2, …, p–1 (2)
k=1, 2, …, p–1 (2)
If aj0
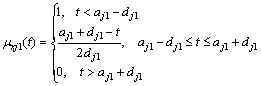 (3)
(3)
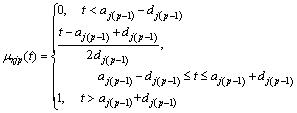 (4)
(4)
 (5)
(5)
where k=2, 3, …, p–1; j=1, 2, …, m.
If aj0>aj1>…>ajp, the single index attribute measure function μxjk(t) is determined as Eqs.(6)– (8):
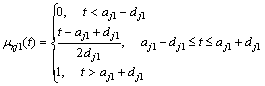 (6)
(6)
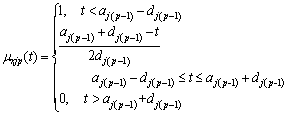 (7)
(7)
 (8)
(8)
where k=2, 3, …, p–1; j=1, 2, …, m.
2.2 Multiple indices synthetic attribute measure analysis
Synthetic attribute measure μxk can be calculated as the following Eq.(9):
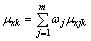 (9)
(9)
where ωj is the weight of the jth index, satisfying
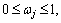
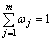 (10)
(10)
2.3 Attribute identification analysis
The purpose of attribute identification is to determine which evaluation rank Ck x belongs to through synthetic attribute measure μxk. In the comprehensive assessment of attribute, evaluation set (C1, C2, …, Cp) is usually an ordered set. The confidence coefficient criterion can be used to evaluate which rank x belongs to through the ordered evaluation set.
The expression of confidence criterion can be expressed as following: in the ordered evaluation set (C1, C2, …, Cp), let C1>C2>…>Cp, or C1
When C1 >C2 >…>Cp, if
 (11)
(11)
it is regarded that x belongs to level Ck0.
When C1
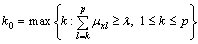 (12)
(12)
it is regarded that x belongs to level Ck0.
3 Attribute evaluation model
3.1 Analysis of influence factors of safe thickness
At present, most studies on factors affecting safe thickness between a concealed karst cave and a karst tunnel are carried out based on the changes of stress field and displacement field of the surrounding rock caused by the karst cave [22, 23]. In order to study the formation and propagation mechanism of fractures around the karst cave filled with water, GUO et al [24] adopted the perturbation method to solve elastic-plastic problem of an oval tunnel with internal action of uniformly distributed pressure. And the plastic zone around the cave is approximately represented as high permeability zone, as shown in Figure 1. The analytical expression of elasticity boundary concerning the first order minor correction is given in Eqs. (13) and (14) as follows:
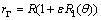 (13)
(13)
where 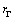 is the polar radius corresponding to polar angle θ in the elastic and plasticity boundary Γ; ε is a parameter related with λ,
is the polar radius corresponding to polar angle θ in the elastic and plasticity boundary Γ; ε is a parameter related with λ, 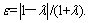
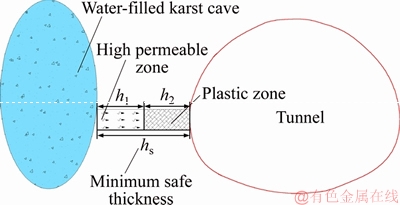
Figure 1 Mechanical model of middle rock pillar instability
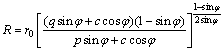 (14)
(14)
where R is radius of the plastic zone, r0 is half sum of semi-major axis and semi-minor axis of the oval, q is a parameter related to crustal stress, φ and c are the internal friction angle and cohesion of surrounding rock, p is internal water pressure in the cave.
When  Eq. (14) should be modified as following,
Eq. (14) should be modified as following,
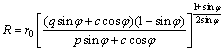 (15)
(15)
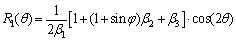 (16)
(16)
where 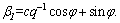
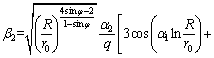
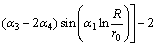 (17)
(17)

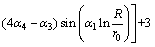 (18)
(18)
where α1, α2, α3 and α4 are parameters related to the mechanical parameter of surrounding rock and oval shape:

 ,
,
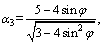
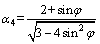
where d1 is a known parameter for the adjustment of the cave shape when ε in load is confirmed. When d1>0, the minor axis of the oval is in vertical direction, that is, on the y-axis. At this time, oval cross section is a flat oval; when d1<0, the minor axis of oval cross section is in horizontal direction, that is, on the x-axis. At this time, oval cross section is a high oval.
From the analysis of Eqs. (14)–(18), it can be seen that the minimum safe thickness between a concealed karst cave and a karst tunnel is affected by many factors, such as physical and mechanical property and structure characteristics of surrounding rock, the size and shape of the karst cave, the filling water pressure, and the distribution conditions of crustal stress. Eight major factors are selected as the evaluation indices of the safe thickness between a karst cave and a karst tunnel, i.e., surrounding rock grade, water pressure in the karst cave, shape of the karst cave, size of the karst cave, attitude of rocks, lateral pressure coefficient of rock mass, tunnel buried depth and relative position of the karst cave and the tunnel.
3.2 Attribute evaluation indices
3.2.1 Physical mechanical parameters I1
There are various factors affecting the stability of surrounding rock. The physical and mechanical properties reflect the basic characteristics of rock mass and they are important factors affecting the stability of tunnel surrounding rock. If the hardness degree of rock is great, the integrity is good, the intensity is high, and anti-deformability of its structural surface is great. Therefore, the stability of surrounding rock during tunnel construction is good and is not easy failure. On the contrary, if the surrounding rock is fractured with low intensity and the structure has weak capacity to resist against deformation, larger deformation will be generated under construction disturbance, which has a great influence on the stability of surrounding rock. The physical and mechanical properties of rock general consist of five parameters, i.e., unit weight, elasticity modulus, Poisson ratio, internal friction angle and cohesion. The physical mechanical parameters are evaluated by those five factors and its affection on safe thickness dangerousness will be divided into four levels for analysis. Details are shown in Table 2.
3.2.2 Water pressure in karst cave I2
High pressure karst water in karst cave can not only weaken mechanical strength indices of surrounding rock but also directly act on surrounding rock as an outer load. High water pressure usually causes great threat to safety in tunnel construction [25–27]. The higher the water pressure in karst cave is, the easier to be deformation and unstable the rock stratum is, and the more easily the water inrush accident happens. Hence, the greater the safe thickness between a concealed karst cave and a karst tunnel is. Therefore, water pressure P in the karst cave is the major factor affecting the safe thickness. The water pressure P is divided into 4 levels, i.e., 0 MPa< P≤0.1 MPa, 0.1 MPa 0.6 MPa.
3.2.3 Shape of karst cave I3
The shapes of karst caves are quite different. Using roundness to simulate a karst cave can not ensure universality. An oval can be used to simulate the different depth-span ratio by changing its long axial and short axial. Therefore, in order to analyze the impact of the karst cave shape on the stress and displacement field of surrounding rock, the karst cave which is approximate to an oval is selected for further study. The stress intensity and stability of surrounding rock are closely related to the shape of the karst cave. The depth-span ratio R is adopted to reflect the shape features of the karst cave. According to related research results [28], safety thickness increases as the depth-span ratio of a karst cave increases when the karst cave is at the side of the tunnel; safety thickness decreases as the depth-span ratio of a karst cave increases when the karst cave is at the top or bottom of the tunnel. That means, under the same conditions, the greater the high-span ratio of a karst cave at the side of the tunnel is, the more dangerous the tunnel is; the smaller the high-span ratio of a karst cave at the top or bottom of the tunnel is, the more dangerous the tunnel is. Therefore, the depth-span ratio R is divided into 4 levels, as shown in Table 3.
3.2.4 Size of karst cave I4
The impact degree of the karst cave with different sizes on deformation of tunnel surrounding rock is different. The bigger the karst cave is, the greater the impact of the karst cave on the change of plasticity zone in tunnel surrounding rock is. And the surrounding rocks between the concealed karst cave and the tunnel may generate greater deformation and cause instability due to stress concentration. According to relevant reference [29], the karst cave span S was used to reflect the size of the karst cave, and it was divided into six levels based on statistical analysis, i.e., S<2 m, 2 m≤S≤6 m, 6 m
Table 2 Grade division of physical mechanical parameters

Table 3 Grade division of depth-span ratio R

3.2.5 Attitude of rocks I5
The extension direction and development degree of the karst fissure determine the development degree, direction and size of the karst cave. Different dip angles of rock stratum directly result in different groundwater recharge, runoff, drainage, infiltration condition, and karst development degree [30]. The rock stratum with horizontal attitude has a poor infiltration condition, and karst development is restricted; the rock stratum with vertical attitude has a small surface water collection area and weak water cycle, therefore, the karst development degree is weak, too. The most beneficial attitude of rocks to karst development is the wing position of syncline or anticline with 25°–65° dip angle [30]. The attitude of rocks can be represented by dip angles of rock stratum φ. The data can be obtained by using geological compass at tunnel site. In order to satisfy the orderliness of attribute mathematics, according to data format requirements of assessment indices shown in Table 1, the dip angle of stratum should be modified. The modified method can refer to Ref. [20], as shown in Table 4.
3.2.6 Lateral pressure coefficient of rock mass I6
Lateral pressure coefficient λ is an important index to describe the magnitude of the horizontal in-situ stress. Under the effect of different lateral pressure coefficient, the state of the tunnel rock will vary too. Under the same buried depth condition, the greater the lateral pressure coefficient is, the worse the rock stability between the concealed karst cave and the tunnel stratum is. The lateral pressure coefficient λ is divided into 4 levels [31], i.e., 0<λ≤1, 1<λ≤1.25, 1.25<λ≤1.5, 1.5<λ≤2.
Table 4 Modified method of dip angle of strata [20]

3.2.7 Tunnel buried depth I7
When the geographical environment of tunnel is different, the in-situ stress conditions of tunnel are also different. The buried depth D is one of the main features of in-situ stress, which determines the size of vertical in-situ stress. In general, the greater the depth is, the greater the stress is, and it is more unfavorable for the stability of the tunnel surrounding rock. The tunnel buried depth D is divided into 4 levels, i.e., 0 m
3.2.8 Relative position of cave and tunnel I8
When the relative position of the karst cave and tunnel is different, the force and deformation of the tunnel are completely different [32], and the variations of the plastic zone of the tunnel surrounding rock is different, too. According to the different degree of impact on the dangers of safe thickness, the relative position of the cave on the tunnel is divided into 4 levels, i.e., safe, basically safe, dangerous and extremely dangerous.
3.3 Grading standards of attribute evaluation index
Based on the analysis above, the evaluation indices of safe thickness between a concealed cave and the karst tunnel are divided into four grades, and the grading of the single evaluation index is shown in Table 5.
3.4 Single index attribute measure function
In Table 5, there are 11 evaluation indices (I1–1–I1–5, I2–I7) whose data satisfy the form requirements in Table 1. The attribute measure function of single index can be established by Eqs. (3)–(8). As a qualitative index, I8 will not be provided with the attribute measure function of single index, and its attribute measure is expressed by 0 or 1. The attribute measure functions of evaluation indices I1–1–I1–5, I2–I7 are shown in Table 6.
3.5 Evaluation index weight
The comprehensive weight method is adopted to confirm factor weight vector [33], as shown in Eqs. (19)–(21):
ω=ωPΨP+ωQΨQ (19)
ωP=[ωp1ωp2 … ωpi … ωpn] (20)
ωQ=[ωq1ωq2 … ωqi … ωqn] (21)
where ωP is an objective weight vector, ωQ is a subjective weight vector, ΨP is assignment weight of objective weight, ΨQ is assignment weight of subjective weight. ωP is obtained by the statistics of typical examples of karst caves. ωQ is obtained from analytic hierarchy process, ΨP and ΨQ are obtained from confidence index method of specialist.
Table 5 Assessment index and classification standard

Table 6 Attribute measure functions of single index

be continued
Continued

3.5.1 Weight analysis of evaluation indices in level 1
1) Objective weight
Through the statistics of 207 typical karst caves in karst tunnels in western mountain areas of Hubei Province, the factors’ weights in evaluation factor set of a concealed cave safe thickness against karst tunnel stratum are obtained, i.e., weight of physical mechanical parameters (ωp1) is 0.260; weight of water pressure in the karst cave (ωp2) is 0.313; weight of karst cave shape (ωp3) is 0.104; weight of karst cave size (ωp4) is 0.125; weight of attitude of rocks (ωp5) is 0.078; weight of lateral pressure coefficient of rock (ωp6) is 0.063; weight of tunnel buried depth (ωp7) is 0.042; relative position of a karst cave and a tunnel (ωp8) is 0.016, and the confidence index (ΨP) is 8.7.
2) Subjective weight
Subjective weight is obtained through the method of analytic hierarchy process [33], and the factor weight vector is calculated by root square value method. The identification matrix of the evaluation model is built in Eq.(22):
 (22)
(22)
The index weight vector is obtained: WA–B= [0.233, 0.392, 0.084, 0.092, 0.087, 0.054, 0.034, 0.024]T, λmax=8.234, consistency index CI=0.033, random consistency ratio CR=0.024<0.1, which satisfies consistency requirements. Confidence index is obtained, i.e., ΨQ=9.1.
3) Weight distribution
After normalization processing of comprehensive weight method, the weight of every index is obtained, i.e., ω=[0.246, 0.353, 0.094, 0.108, 0.083, 0.058, 0.038, 0.020]T.
3.5.2 Weight analysis of evaluation indices in level 2
The method of analytic hierarchy process is adopted for analysis, and the identification matrix of evaluation model is shown in Table 7.
Table 7 Comparison matrix of assessment model

where λmax is the maximum characteristic value of the comparison matrix, CI is consistency index, CR is random consistency ratio.
4 Engineering application 1
4.1 General situation of project
Huangtupo No.1 tunnel is a separated tunnel in expressway from Enshi to Laifeng. The beginning and the end mileage is ZK39+647–ZK40+620 in left line of the tunnel, YK39+672–YK40+607 in right line of the tunnel. The maximum buried depth of the tunnel is about 160.5 m. The tunnel belongs to hill clinoform with peak-cluster landform. A huge karst funnel develops at the exit. Five ponors with different sizes are continuously distributed along the bottom long axis of the funnel. Slope around funnel is about 20°–70°, and part position is approximate to upright escarpment. The stratum is limestone and dolomite limestone. Joints and fissures well develop in rock mass around tunnel site. And the attitude of rocks is about 280°–42°∠19°–48°, where huge karst caves are easy to develop.
On October 26, 2012, a karst cave was found in the face of left line at ZK40+231 in Huangtupo No.1 tunnel [34]. The karst cave extends from right side haunch to left side skewback. The cave is 6 m in length and has a outspreading trend towards forwards right, and it is about 8 m in width, about 20–30 m in height. The karst cave is filled with sediment and water. The water pressure in the karst cave is measured, i.e., 0.53 MPa. According to the geological survey report, there are dolomite and dolomite limestone at the exit ZK40+231 of Huangtupo No.1 Tunnel, and its stratum dip angle changes gradually from 29° to 18°. After correction, stratum dip angle is 25°. In the area of ZK40+170–ZK40+180 and ZK40+370–ZK40+380, ponor develops in the ground surface, which is easy to produce catchments. At ZK40+231, the tunnel buried depth is 150 m, and the surrounding rock grade is level IV. The unit weight of overlying rock is 23.0 kN/m3, the lateral pressure coefficient is 1.26, the elastic modulus is 1.396 GPa, the cohesion is 0.54 MPa, the internal friction angle is 33°, and the Poisson ratio is 0.32.
The established attribute cognition model of safe thickness evaluation between a concealed cave and the karst tunnel is adopted to evaluate the safe thickness at the exit ZK40+231 of Huangtupo No.1 Tunnel.
4.2 Single index attribute measurement and synthetic attribute measurement
According to the sample data in Table 8 and the single index attribute measure function in Table 6, single index attribute measure is calculated. According to Eq. (9), synthetic attribute measure of the sample is calculated. And the results can be seen in Table 8.
4.3 Analysis of attribute identifications
Since that the higher the level of safety is, the better it is, the evaluation set (C1, C2, C3, C4) is an ordered set, i.e., C1>C2>C3>C4. It is identified according to confidence criterion Eq. (9). Considering the safety of tunnel construction, λ is taken as 0.7 in design stage [21], then Eq. (9) is simplified as
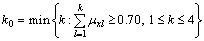 (23)
(23)
After calculation, the safe thickness in Huangtupo No.1 tunnel is in C3 level, and has quite high dangerousness. After the karst cave was revealed, mud and water flowed downwards constantly into the tunnel with a water inflow about 2 m3/h. The sediment was from tunnel face to ZK40+216 with about 2 m in height, as shown in Figure 2. The result is consistent with the result that water and mud inrush occurred during excavation.
Table 8 Calculation table of attribute measures
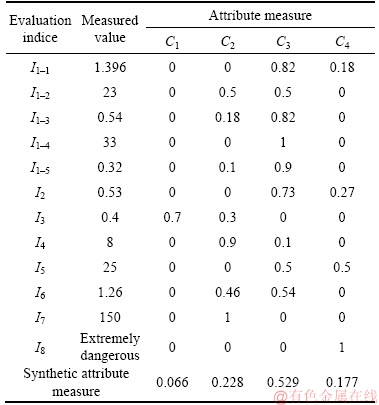

Figure 2 Diagram of tunnel water and mud inrush [34]
4.4 Treatment measure of karst cave
1) The mud from ZK40+231 to ZK40+216 in the tunnel was removed, and several site drainage measures were properly taken.
2) The characteristics of backfill materials had a great influence on engineering stability [35–38]. Tunnel mucking was adopted to backfill the karst cave to 2 m under the vault at ZK40+227– ZK40+231; The C20 concrete were pumped up to 2 m above the vault and 2 m below the vault in the cave, and 4 d110 mm drain-pipes was reserved.
3) “SF-V a Composite lining” was adopted as auxiliary construction at ZK40+227–ZK40+237. Advanced small pipes were added. The pipes were made of hot-rolling seamless pipes with 42 mm outer diameter and 3.5 mm wall thickness. The front end of the pipes is pointed cone shape, and tail part were welded with 6 ribbings. And the pipe wall was drilled with 8 mm grout holes. During the construction of advanced small pipes, the steel pipes were in parallel with the lining center line and were driven into the arch surrounding rock with an elevation angle of 5°–10°. And the distance between steel pipes in ring direction was 40 cm. After finishing each row advanced small pipes and grouting, the construction process was: excavating the arch part, spraying concrete and erecting steel frame. And after finishing early supports, another row of steel pipes were driven in with a 2.4 m interval. The advanced small pipes of different rows had a splicing length more than 1.0 m. The schematic diagram is shown in Figure 3.
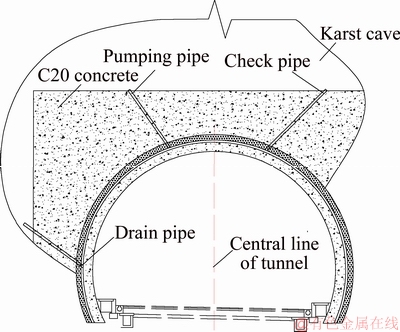
Figure 3 Schematic diagram of treatment of karst cave [34]
4) Cement grout (adding sodium silicate accounting for 5% cement weight) was adopted as the advanced small pipe grout material. And the parameters were as follows: The water cement ratio was 1:1; the concentration of sodium silicate was 35 Baume degree and its modulus was 2.4; the grouting pressure ranged from 0.5–1.0 MPa.
5) After grouting, the up and down bench excavation method was adopted. Before excavation, the surrounding rock 20 m in front of tunnel face should be clearly explored by long drill pipe to observe whether there was mud and water inrush. If yes, it should be reported to the superior and the excavation could continue only after proper treatment.
6) The original running water access should be kept smooth. And in outer edge of the early supports, 4 d110 mm HDPE double-wall drilling corrugated pipes were buried with a 2 m longitudinal distance, and they were connected with the permanent drainage system in the cave.
5 Engineering application 2
5.1 General situation of project
Qiyueshan tunnel is the key project of the connecting line of Moudao town and Lichuan- Wanzhou expressway. It is located between Nanping township and Moudao town of Lichuan city, Hubei Province. The tunnel consists of a single tube. The tunnel is 2960 m long, starting from GK0+350 to GK3+310. The maximum buried depth of the tunnel is about 347 m. The tunnel site belongs to tectonic dissolution-denudation medium mountain landform. The tunnel traverses the mountain ridge. The surface elevation ranges 1260 from 1660 m. The terrain appeared rise and fall wavily as a whole. Karst micro-geomorphologic develops, such as karst channelings, troughs, grooves, funnels and sinkholes. The surface of tunnel site is partially covered with Quaternary residual silty clay. The underlying bedrocks are Permian limestone with intercalation of coal and shale, Triassic limestone and part of it with intercalation of thin layers of shale. Karst develops in this area. The main geological structures that the tunnel passes through are Qiyueshan Anticline and Qiyueshan Fault, where large karst caves are prone to develop.
On January 5, 2015, a karst cave was detected above the arch springing line at GK0+437 of the tunnel. The karst cave is about 5 m in length, 4 m in width, and 15 m in height. It is filled with mud and stones. It is about 53 m from the vault of the tunnel to the ground surface. There is no subsidence at the ground surface. The original designed surrounding rock grade is level III. The actual excavated surrounding rock grade is level V. The physical mechanical parameters are as following: the elastic modulus is 2 GPa; the unit weight of rock is 25 kN/m3; the cohesion is 0.6 MPa; the internal friction angle is 50°; and the Poisson ratio is 0.25. The water pressure is represented by the soil pressure in the karst cave, which is 0.27 MPa. The dip angle is 72° and it is 18° after correction. The lateral pressure coefficient is 0.8.
The established attribute cognition model of safe thickness evaluation between a concealed cave and the karst tunnel is also adopted to evaluate the safe thickness at the exit GK0+437 of Qiyueshan tunnel.
5.2 Single index attribute measurement and synthetic attribute measurement
According to the sample data in Table 9 and the single index attribute measure function in Table 6, single index attribute measure is calculated. According to Eq. (9), synthetic attribute measure of the sample is calculated. And the results can be seen in Table 9.
Table 9 Calculation table of attribute measures
5.3 Analysis of attribute identifications
The identification equation is the same as Eq. (23). After calculation, the evaluation safety level at GK0+437 in Qiyueshan tunnel is in C3 level which is medium potential dangerousness. During the excavation at GK0+437, about 50 m3 mud and stones collapsed from the karst cave and entered into the tunnel [39], as shown in Figure 4. The assessment result is consistent with the result that mud and stone collapsed occurred during excavation.
5.4 Treatment measure of karst cave
The treatment construction was from GK0+437 to GK0+447. An intensive “V support form” was adopted. It consisted of primary support, waterproof layer and secondary lining. The primary support was composed of system rock bolts, d8 steel mesh with a spacing of 20 cm×20 cm, 24 cm thick C20 shotcrete and I18 steel arch frame with a longitudinal spacing of 50 cm. The system rock bolts were d42 grouting small pipes which were 3 m long. They were arranged with the spacing of 0.5 m in longitudinal direction, 1.0 m in ring direction and presented as a plum blossom mold. The waterproof layer was performed between the primary support and secondary lining and it was composed of waterproof board and nonwoven geotechnical fabric. The secondary lining was 45 cm thick C25 reinforced concrete. In addition, the advanced small pipes grouting method was adopted as auxiliary construction to keep the stability of surrounding rock. The advanced small pipes were 5 m long. They were arranged with the spacing of 1.0 m in longitudinal direction and 0.2 m in ring direction. The karst cave was filled by pumping C20 concrete. The pumped concrete was more than 1.5 m thick from the outline of primary support. Drain pipes were reserved and connected with the longitudinal drainage system of the tunnel.

Figure 4 Picture of mud and stones collapsed [39]
6 Conclusions
1) Based on the attribute mathematical theory, an attribute recognition model of safe thickness evaluation between a concealed cave and the karst tunnel is established. The perturbation method is employed to calculate the plastic zone radius of an oval tunnel. Hereby, eight major factors are selected as safe thickness evaluation indices between a concealed cave and the karst tunnel stratum, i.e., physical mechanical parameters of rock mass, water pressure in the karst cave, karst cave shape, karst cave size, attitude of rocks, lateral pressure coefficient of rock mass, tunnel buried depth, and relative position of a karst cave and a tunnel. The attribute measure function is established to calculate the single index attribute measure and the sample synthetic attribute measure. At last, the confidence criterion is used to carry out an attribute identification on the safe thickness between the tunnel sample and a karst cave. It provides an effective method for safe thickness evaluation of a concealed cave and the karst tunnel.
2) The established attribute recognition model is used to evaluate the karst caves of Huangtupo No.1 tunnel on Enshi-Laifeng and Enshi-Qianjiang expressways and Qiyueshan tunnel on the Moudao connecting line of Lichuan-Wanzhou expressway. The contrastive analyses of site operation situations and assessment results show that the assessment results are consistent with the excavation situations, which prove that the applications of attribute mathematical theory to the safe thickness evaluation between a concealed cave and the karst tunnel are reasonable and feasible.
3) According to the assessment results, reasonable treatment schemes are respectively adopted for the karst cave filled with water in Huangtupo No. 1 tunnel and the karst cave filled with mud in Qiyueshan tunnel, which ensure the safety of the tunnel’s construction and effectively prevent the lives and property losses possibly caused by the water and mud inrush disasters.
References
[1] LI Shu-cai, XU Zhen-hao, HUANG Xin, LIN Peng, ZHAO Xiao-cheng, ZHANG Qing-song, YANG Lei, ZHANG Xiao, SUN Huai-feng, PAN Dong-dong. Classification, geological identification, hazard mode and typical case studies of hazard-causing structures for water and mud inrush in tunnels [J]. Chinese Journal of Rock Mechanics and Engineering, 2018, 37(5): 1041–1069. DOI: 10.13722/ j.cnki.jrme.2017.1332. (in Chinese)
[2] WANG Jing, LI Shu-cai, LI Li-ping, LIN Peng, XU Zhen-hao, GAO Cheng-lu. Attribute recognition model for risk assessment of water inrush [J]. Bulletin of Engineering Geology and the Environment, 2019, 78(2): 1057–1071. DOI: 10.1007/s10064-017-1159-4.
[3] WANG Xin-tong, LI Shu-cai, XU Zhen-hao, LIN Peng, HU Jie, WANG Wen-yang. Analysis of factors influencing floor water inrush in coal mines: A nonlinear fuzzy interval assessment method [J]. Mine Water and the Environment, 2019, 38(1): 81–92. DOI: 10.1007/s10230-018-00578-x.
[4] WANG Xin-tong, LI Shu-cai, XU Zhen-hao, HU Jie, PAN Dong-dong, XUE Yi-guo. Risk assessment of water inrush in karst tunnels excavation based on normal cloud model [J]. Bulletin of Engineering Geology and the Environment, 2018. DOI: 10.1007/s10064-018-1294-6.
[5] XU Zhen-hao, WANG Xin-tong, LI Shu-cai, GAO Bin, SHI Shao-shuai, XU Xin-ji. Parameter optimization for the thickness and hydraulic conductivity of tunnel lining and grouting rings [J]. KSCE Journal of Civil Engineering, 2019. DOI: 10.1007/s12205-019-1509-9.
[6] SONG K I, CHO G C, CHANG S B. Identification, remediation, and analysis of karst sinkholes in the longest railroad tunnel in South Korea [J]. Engineering Geology, 2012, 135–136: 92–105. DOI: 10.1016/j.enggeo.2012. 02.018.
[7] HUANG Fu, ZHAO Lian-heng, LING Tong-hua, YANG Xiao-li. Rock mass collapse mechanism of concealed karst cave beneath deep tunnel [J]. International Journal of Rock Mechanics and Mining Sciences, 2017, 91: 133–138. DOI: 10.1016/j.ijrmms.2016.11.017.
[8] CUI Qing-long, WU Huai-na, SHEN Shui-long, XU Ye-shuang, YE Guan-lin. Chinese karst geology and measures to prevent geohazards during shield tunnelling in karst region with caves [J]. Natural Hazards, 2015, 77(1): 129–152. DOI: 10.1007/s11069-014-1585-6.
[9] ZHAO Yan-lin, PENG Qing-yang, WAN Wen, WANG Wei-jun, CHEN Bin. Fluid-solid coupling analysis of rock pillar stability for concealed karst cave ahead of a roadway based on catastrophic theory [J]. International Journal of Mining Science and Technology, 2014, 24(6): 737–745. DOI: 10.3969/j.issn.2095-2686.2014.06.003.
[10] JIANG Chong, ZHAO Ming-hua, CAO Wen-gui. Stability analysis of subgrade cave roofs in karst region [J]. Journal of Central South University of Technology, 2008, 15(s2): 38–44. DOI: 10.1007/s11771-008-0433-9.
[11] YANG Xiao-li, XIAO Hai-bo. Safety thickness analysis of tunnel floor in karst region based on catastrophe theory [J]. Journal of Central South University, 2016, 23(9): 2364–2372. DOI: 10.1007/s11771-016-3295-6.
[12] LAI Yong-biao, WANG Meng-shu, YOU Xin-hua. Study of safe distance criterion between concealed karst cave and tunnel [J]. Applied Mechanics and Materials, 2014, 556–562: 849–852. DOI: 10.4028/www.scientific.net/AMM.556-562. 849.
[13] JIANG Hai-ming, LI Lang, RONG Xiao-li, WANG Ming-yang, XIA Yuan-pu, ZHANG Zhi-cheng. Model test to investigate waterproof-resistant slab minimum safety thickness for water inrush geohazards [J]. Tunnelling and Underground Space Technology, 2017, 62: 35–42. DOI: 10.1016/j.tust.2016.11.004.
[14] LI Shu-cai, ZHOU Zong-qing, YE Zhi-hua, LI Li-ping, ZHANG Qian-qing, XU Zhen-hao. Comprehensive geophysical prediction and treatment measures of karst caves in deep buried tunnel [J]. Journal of Applied Geophysics, 2015, 116: 247–257. DOI: 10.1016/j.jappgeo.2015.03.019.
[15] SONG Zhan-ping, LI Ning, DENG Liang-sheng. Analysis of minimum thickness of tunnel floor and collapse mechanism of rock stratum in karst tunnel (Yuan Si ed.) [C]// Proceedings of the 15th National Conference on Structural Engineering, Jiaozuo, Henan. Beijing: Engineering Mechanics Press, 2006: 336–339. (in Chinese)
[16] CHENG Qian-sheng. Attribute recognition theoretical model with application [J]. Universitatis Pekinnensis, Acta Scientianrum Naturalium, 1997, 33(1): 12–20. DOI: 10.13209/j.0479-8023.1997.002. (in Chinese)
[17] CHENG Qian-sheng. Attribute sets and attribute synthetic assessment system [J]. Systems Engineering-Theory & Practice, 1997, 17(9): 1–8. DOI: 10.12011/1000- 6788(1997)9-2. (in Chinese)
[18] CHENG Qian-sheng. Attribute mathematics-Attribute measurement and attribute statistics [J]. Mathematics in Practice and Theory, 1998, 28(2): 97–107. (in Chinese)
[19] CHU Han-dong, XU Guang-li, YASUFUKU N, YU Zhang, LIU Po-la, WANG Ji-feng. Risk assessment of water inrush in karst tunnels based on two-class fuzzy comprehensive evaluation method [J]. Arabian Journal of Geosciences, 2017, 10: 179. DOI: 10.1007/s12517-017-2957-5.
[20] ZHOU Zong-qing, LI Shu-cai, LI Li-ping, SHI Shao-shuai, SONG Shu-guang, WANG Kai. Attribute recognition model and its application of fatalness assessment of water inrush in karst tunnels [J]. Rock and Soil Mechanics, 2013, 34(3): 818–826. DOI: 10.16285/j.rsm.2013.03.024. (in Chinese)
[21] LI Shu-cai, ZHOU Zong-qing, LI Li-ping, XU Zhen-hao, ZHANG Qian-qing, SHI Shao-shuai. Risk assessment of water inrush in karst tunnels based on attribute synthetic evaluation system [J]. Tunnelling and Underground Space Technology, 2013, 38: 50–58. DOI: 10.1016/j.tust.2013. 05.001.
[22] CRISS E M, CRISS R E, OSBURN G R. Effect of stress on cave passage shape in karst terranes [J]. Rock Mechanics and Rock Engineering, 2008, 41(3): 499–505. DOI: 10.1007/ s00603-006-0106-7.
[23] LI Shu-cai, WU Jing, XU Zhen-hao, ZHOU Lun, ZHANG Bo. A possible prediction method to determine the top concealed karst cave based on displacement monitoring during tunnel construction [J]. Bulletin of Engineering Geology and the Environment, 2019, 78(1): 341–355. DOI: 10.1007/s10064-017-1060-1.
[24] GUO Jia-qi, QIAO Chun-sheng, CAO Xi. Research on safe thickness of rock pillar between the tunnel and adjacent karst cave with pressurised water [J]. Modern Tunnelling Technology, 2010, 47(6): 10–16. DOI: 10.3969/j.issn. 1009-6582.2010.06.002. (in Chinese)
[25] GUO Jia-qi, REN Lian-wei, LIU Xi-liang. Study on safe thickness of comparatively intact rock ahead of karst tunnel face [J]. Applied Mechanics and Materials, 2011, 90–93: 2456–2459. DOI: 10.4028/www.scientific.net/AMM.90-93. 2456.
[26] HONG E S, PARK E S, SHIN H S, KIM H M. Effect of a front high hydraulic conductivity zone on hydrological behavior of subsea tunnels [J]. KSCE Journal of Civil Engineering, 2010, 14(5): 699–707. DOI: 10.1007/s12205- 010-0838-5.
[27] PAN Dong-dong, LI Shu-cai, XU Zhen-hao, LI Li-ping, LU Wei, LIN Peng, HUANG Xin, SUN Shang-qu, GAO Cheng-lu. Model tests and numerical analysis for water inrush caused by karst caves filled with confined water in tunnels [J]. Chinese Journal of Geotechnical Engineering, 2018, 40(5): 828–836. DOI: 10.11779/CJGE201805007. (in Chinese)
[28] CAO Xi. Study on safe thickness for rock between tunnel and karst cave in karst region [D]. Beijing: Beijing Jiaotong University, 2010. (in Chinese)
[29] SONG Zhan-ping. Research on the influence of concealed karst caverns upon the stability of tunnels and its support structure [D]. Xi’an: Xi’an University of Technology, 2005. (in Chinese)
[30] XU Zhen-hao, LI Shu-cai, LI Li-ping, HOU Jian-gang, SUI Bin, SHI Shao-shuai. Risk assessment of water or mud inrush of karst tunnels based on analytic hierarchy process [J]. Rock and Soil Mechanics, 2011, 32(6): 1757–1766. DOI: 10.16285/j.rsm.2011.06.038. (in Chinese)
[31] HUANG Xin, LI Shu-cai, XU Zhen-hao, GUO Ming, CHEN Yu-cheng. Assessment of a concealed karst cave’s influence on karst tunnel stability a case study of the Huaguoshan tunnel, China [J]. Sustainability, 2018, 10: 2132. DOI: 10.3390/su10072132.
[32] DENG Qing-hai, MA Feng-shan, GUO Jie, ZHANG Li-ping, YU Rui. The effect of karst cave space distribution on deformation law of double track tunnel surrounding rock [J]. Advanced Materials Research, 2012, 374–377: 2446–2451. DOI: 10.4028/www.scientific.net/AMR.374-377.2446.
[33] XU Zhen-hao, LI Shu-cai, LI Li-ping, CHEN Jun, SHI Shao-shuai. Construction permit mechanism of karst tunnels based on dynamic assessment and management of risk [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(11): 1715–1725. (in Chinese)
[34] GUO Ming. Study on concealed karst cave's influence on karst tunnel stability and treatment technology on tunnels of E-xi mountainous [D]. Ji’nan: Shandong University, 2014. (in Chinese)
[35] LIU Lang, ZHU Chao, QI Chong-chong, ZHANG Bo, SONG Ki-il. A microstructural hydration model for cemented paste backfill considering internal sulfate attacks [J]. Construction and Building Materials, 2019, 211: 99–108. DOI: 10.1016/j.conbuildmat.2019.03.222.
[36] LIU Lang, YANG Pan, QI Chong-chong, ZHANG Bo, GUO Li-jie, SONG Ki-il. An experimental study on the early-age hydration kinetics of cemented paste backfill [J]. Construction and Building Materials, 2019, 212: 283–294. DOI: 10.1016/j.conbuildmat.2019.03.322.
[37] WANG Mei, LIU Lang, ZHANG Xiao-yan, CHEN Liu, WANG Shi-qi, JIA Yu-hang. Experimental and numerical investigations of heat transfer and phase change characteristics of cemented paste backfill with PCM [J]. Applied Thermal Engineering, 2019, 150: 121–131. DOI: 10.1016/j.applthermaleng.2018.12.103.
[38] ZHAO Yu-jiao, LI Ruo-yao, JI Chang-fa, HUAN Chao, ZHANG Bo, LIU Lang. Parametric study and design of an earth air heat exchanger using model experiment for memorial heating and cooling [J]. Applied Thermal Engineering, 2019, 148: 838–845. DOI: 0.1016/ j.applthermaleng.2018.11.018
[39] ZHOU Lun. Prediction method of concealed karst cave based on displacement monitoring and analysis of the tunnel rock deformation characteristics [D]. Ji’nan: Shandong University, 2017. (in Chinese)
(Edited by HE Yun-bin)
中文导读
隐伏溶洞与隧道间安全厚度评估的属性识别模型
摘要:基于属性数学理论建立了隐伏溶洞与隧道岩层间安全厚度风险评估的属性识别模型,用于开展隐伏溶洞与隧道岩层间安全厚度危险性分级,确保隧道工程施工安全。首先,采用摄动法确定溶洞与隧道岩层安全厚度的评估指标与危险性分级标准,然后,通过构造属性测度函数以计算单指标属性测度和样本综合属性测度,最后,应用置信度准则对隧道样本与溶洞间安全厚度进行属性识别。开展两个工程实例应用研究。结果表明,评价结果与现场揭示结果有较好的一致性,为隧道溶洞治理方案的实施提供了正确的指导。
关键词:隐伏溶洞;岩溶隧道;安全厚度;属性识别
Foundation item: Projects(51509147, 51879153) supported by the National Natural Science Foundation of China; Projects(2017JC002, 2017JC001) supported by the Fundamental Research Funds of Shandong University, China
Received date: 2018-04-16; Accepted date: 2018-11-07
Corresponding author: XU Zhen-hao, PhD, Professor; Tel: +86-531-88395428; E-mail: zhenhao_xu@sdu.edu.cn; ORCID: 0000-0002- 6578-7583; ZHANG Bo, PhD, Associate Professor; Tel: +86-531-88395371; E-mail: zhangbo1977@sdu.edu.cn; ORCID: 0000-0002-5801-2819

