J. Cent. South Univ. Technol. (2009) 16: 0154-0159

DOI: 10.1007/s11771-009-0026-2

Application of empirical mode decomposition based energy ratio to vortex flowmeter state diagnosis

SUN Zhi-qiang(孙志强)¹, ZHANG Hong-jian(张宏建)²

(1. School of Energy Science and Engineering, Central South University, Changsha 410083, China;

2. Department of Control Science and Engineering, Zhejiang University, Hangzhou 310027, China)

Abstract: To improve the measurement performance, a method for diagnosing the state of vortex flowmeter under various flow conditions was presented. The raw sensor signal of the vortex flowmeter was adaptively decomposed into intrinsic mode functions using the empirical mode decomposition approach. Based on the empirical mode decomposition results, the energy of each intrinsic mode function was extracted, and the vortex energy ratio was proposed to analyze how the perturbation in the flow affected the measurement performance of the vortex flowmeter. The relationship between the vortex energy ratio of the signal and the flow condition was established. The results show that the vortex energy ratio is sensitive to the flow condition and ideal for the characterization of the vortex flowmeter signal. Moreover, the vortex energy ratio under normal flow condition is greater than 80%, which can be adopted as an indicator to diagnose the state of a vortex flowmeter.

Key words: flow state diagnosis; energy ratio; vortex flowmeter; empirical mode decomposition

1 Introduction

Vortex flowmeter is based on the linear relationship between the average fluid velocity and the vortex shedding frequency in Karman vortex street wake[1]. The application of vortex flowmeter in the process industries is becoming increasingly widespread, particularly in the measurement where flowmeters with no moving parts and wide rangeability are required. With recent decades of development, the vortex flowmeter has belonged to the leading group of devices currently used for flow measurement[2].

Customarily, sensor signals of vortex flowmeter are processed either to give the reading of measured fluid on site or to transmit the flow rate signal to control devices in the standard 4-20 mA direct current form or the pulse train version[3]. In those signal output forms, the effects such as pipe vibration and fluid pulsation on the performance of vortex flowmeter are difficult to be recognized even though sometimes the outputs are already meaningless for the measurement. The operators can not validate a vortex flowmeter measurement while it is working. However, if the flowmeter signal is examined before it is conditioned to standard form, the information that is more representative of the dynamic nature of the flow may be obtained. The vortex flowmeter is also considered to be ideally suitable for studying the response of the measurement system to the flow regime, in which it is operating[4]. Therefore, it is important and advisable to investigate the characteristic relationship between the unconditioned sensor signal of vortex flowmeter and the flow perturbation, which is helpful to enhancing the quality of the measurement information output from the vortex flowmeter and hence improving the performance of vortex flowmeter.

Most studies related to vortex flowmeters were focused on the processing of vortex signal[5-7] or the optimization of bluff body configuration[8-10]. Recently, some studies[11-13] have shown that the pulse output signals of vortex flowmeter could be processed not only to provide the basic measurement of the flow rate, but also to provide information that could indicate the condition of the flowmeter. In fact, measurements of flow rate and information related to the flowmeter can be obtained concurrently from the flowmeter signal. However, as discussed in Ref.[4], some perturbation in the flow could not be discerned in the power spectra, which implies that the spectral analysis may not be sufficiently sensitive to perturbations and other signal processing method should be adopted.

The objective of this work is to extract the characteristics of the vortex flowmeter from raw sensor signals using the empirical mode decomposition (EMD) technique, and then to establish the relationship between the characteristic parameter and the flow conditions. The EMD method is an inseparable step of the Hilbert-Huang transform (HHT), which is especially suitable for the exploration of the local properties of a signal.

2 Proposed method and simulation

The Hilbert-Huang transform is a quite new time-frequency analysis method[14]. The main difference between HHT and other methods lies in that the elementary function of HHT is derived from the signal adaptively. The main feature of HHT is the EMD method, which is capable of extracting all the oscillatory modes embedded in a signal. Each extracted mode is referred to as an intrinsic mode function (IMF), and each IMF has a unique local characteristic. Therefore, the EMD method is regarded as the core of HHT. The most important advantage of HHT over other methods is that it can deal with the non-linear problem objectively[15-16]. It has been proved in Ref.[17] that HHT is an effective technique for denoising the vortex flowmeter signal.

The EMD approach is an adaptive technique that decomposes the original signal into a series of IMF components. Each component represents the local embedded characteristics of the signal. An IMF must satisfy two conditions: one is in the whole data set, the number of extrema and the number of zero-crossings must either equal or differ at most by one, and the other is at any point, the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero. The decomposition of time series x(t) can be carried out through the following steps[16].

(1) Identify all the local minima and maxima of x(t). Then use the cubic spline interpolation to define the upper envelope x_max(t) and the lower envelope x_min(t) of x(t). The mean envelope m₁(t) of the upper and lower envelopes is

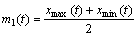                                 (1)

(2) Subtracting m₁(t) from x(t) gives

                          (2)

(3) In general, h₁(t) is just an IMF candidate that can not satisfy all the requirements of an IMF. Iterate the above procedure for k times until the mean envelop is close to zero. So the first IMF component I₁(t) that contains the highest frequency component of the signal can be designated as

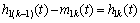,               (3)

In order to avoid obliterating the physically meaningful amplitude fluctuations, a stop criterion for the sifting process is pre-defined[14].

(4) Separate I₁(t) from the rest of x(t). The residue, r₁(t), is treated as the new data series. Since the residue r₁(t) still contains much information of lower frequency components, it is subjected to the same sifting process. Repeat the above procedure on the subsequent residual r_i(t) until the range of the residue is less than a pre-determined value or the residue contains the lowest frequency component. The result obtained is as follows.

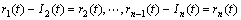       (4)

where r_n(t) denotes the trend of the signal, from which no more IMFs can be extracted and I_n is the nth IMF. Each IMF contains lower frequency components than that extracted just before. At the end of the EMD procedure, signal x(t) can be exactly reconstructed using a linear combination:

                          (5)

In order to validate this decomposition, a simulated time series synthesized by three sinusoidal components and a random noise was processed by the EMD algorithm. Fig.1 shows the EMD results of the simulated signal. The amplitudes of the three sinusoidal components are all 1 V, and their frequencies are 20, 50 and 80 Hz respectively. The variance of the random noise component is 0.09. It is seen that the simulated signal is adaptively decomposed into nine IMFs, and the three sinusoidal components are separated clearly from the signal, as represented by the IMFs6-8. The final  residue is neglected and is not given in Fig.1, because the frequency of the residue is very close to zero, which means that the final residue has little effect on the dynamic vortex component. Furthermore, to investigate the attenuation property of the EMD method, the energy of signal x_k(t) (k = 1, 2, …, N) is defined as

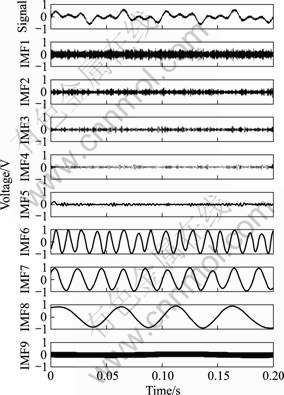
Fig.1 EMD results of simulated signal

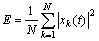                                                       (6)

The energy ratio of IMF6, IMF7, IMF8, and the sum of other IMFs to the total signal is 31.6?31.2?29.9?7.3. Compared with the original energy ratio of the three sinusoidal components and the random noise to the total original signal 31.4?31.4?31.4?5.8, it is found that the energy of each component may attenuate to some extent after the EMD processing, but the energy ratios of different components keep nearly invariant. This property is helpful to the analysis of the vortex signal, because it reveals that the energy ratio of vortex to the total signal energy could be used as a characteristic parameter to indicate the state of vortex flowmeter regardless of EMD. Here, we denote the vortex energy ratio as R with the definition:

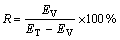                                      (7)

where E_V and E_T denote the energy of the vortex component and the total signal, respectively.

3 Experiment and discussion

3.1 Experimental set-up and flow condition

The experiments were conducted in a circular pipe with diameter of 50 mm. Fig.2 shows the layout of the experiment rig. In front of the test section where the measured signals were collected, there was a gas-liquid mixer connecting the two branches of water and air. Water was the medium to be measured while air was used to produce perturbation in the flow. The flow rates of water and air were measured respectively by an electromagnetic flowmeter and a rotameter before they entered into the mixer. In the experiments, the water flow rate was 5.0-19.0 m³/h, and the air flow rate was 0.1-6.0 m³/h. Additionally, the pressure and temperature of air and water were also measured. The vortex flowmeter tested had a trapezoidal bluff body, and the blockage ratio was 0.28. The duct-wall differential pressure method (DDPM) was adopted to obtain the vortex signals[18-19].

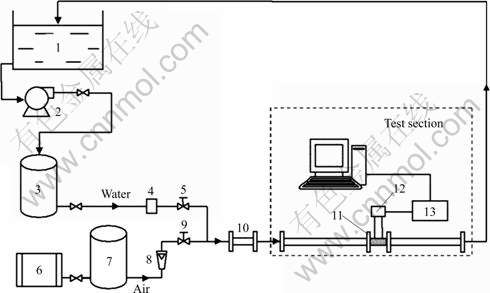
Fig.2 Schematic diagram of experiment rig: 1—Water tank; 2—Pump; 3—Water surge tank; 4—Electromagnetic flowmeter; 5—Valve; 6—Air compressor; 7—Air surge tank; 8—Rotameter; 9—Valve; 10—Mixer; 11—Vortex flowmeter; 12—Sensor and signal conditioner; 13—Oscilloscope

The experiments were carried out under four different flow conditions in which the Karman vortex shedding exists. For the convenience of subsequent discussion, we name them the normal, the pulsating, the bubbly and the unsteady bubbly flow conditions: the normal represents the condition with single water flowing smoothly; the pulsating is the condition for single water measurement, but tapping on the pipe is applied deliberately; the bubbly is the condition, in which a small amount of air is introduced into the water but the volume void fraction is restricted to be less than 5%; the unsteady bubbly is similar to the bubbly except that the volume void fraction of the introduced air is 5%-15% and vortex shedding becomes a little unsteady. It should be noted that the distinction of various flow conditions is based on the time domain signal displayed on site by an oscilloscope during the experiments.

3.2 EMD results of measured signals

Fig.3 shows the IMFs of the vortex flowmeter signals obtained under the four different flow conditions defined above. Different signals have different numbers of IMFs, and different IMFs have different local frequencies. For a fixed signal, the high-frequency components precede the low-frequency ones in the decomposition result. The position of the IMF component corresponding to the vortex shedding signal (vortex component) also varies with flow conditions. It is interesting that the vortex component in Figs.3(a)-(d) are IMF2, IMF3, IMF4 and IMF5 in turn.

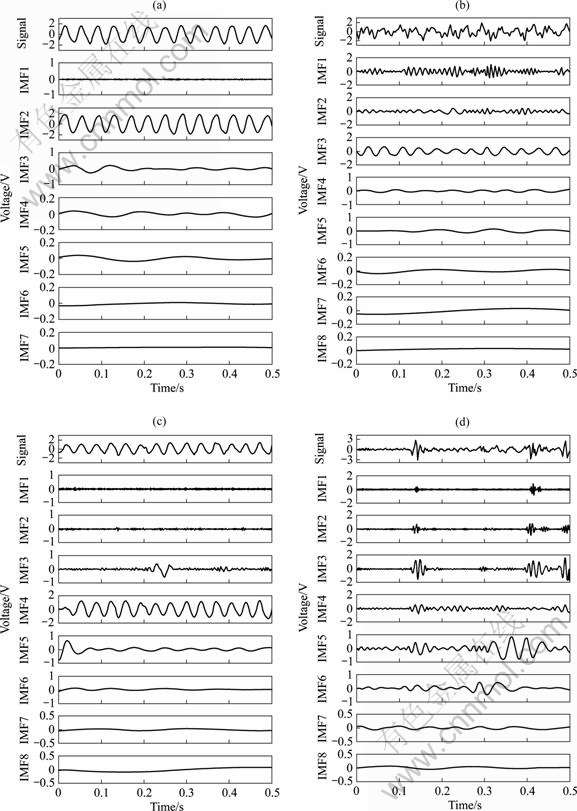
Fig.3 EMD results of measured vortex flowmeter signals: (a) Under normal condition; (b) Under pulsating condition; (c) Under bubbly condition; (d) Under unsteady bubbly condition

By inspecting the EMD results of various flow conditions, it is also found that the tapping on pipe and the introduction of air both have significant effects on the signal quality of a vortex flowmeter. However, their effects are not uniform. Taking the signal obtained under the normal condition as the reference, the effect of the tapping is mainly dominant in the higher-frequency band because the amplitudes of IMF1 and IMF2 in Fig.3(b) are rather greater than that of IMF1 in Fig.3(a). But at the same time, the cases of the lower-frequency band in Figs.3(a) and (b) are quite similar. Note that the higher- or lower-frequency component mentioned here represents the component whose frequency is greater or less than the vortex component. From Figs.3(c) and (d), the effect of the introduced air or bubble is demonstrated. Small amount of air in water causes a little variation in the signal regardless of the frequency. While with the increase of air, the measured vortex flowmeter signal deteriorates markedly, that is, the perturbation of the components appears in both the higher- and lower-frequency bands. Furthermore, the vortex component IMF5 in Fig.3(d) begins to become unsteady.

According to the definition in Eqns.(6) and (7), the energy of all IMFs in the measured signal was computed, and then the ratio of the vortex component energy to the total signal energy was obtained. Fig.4 illustrates the distribution of the vortex energy ratio (R) under various flow conditions. The top horizontal ordinate represents the vortex frequency corresponding to the flow rate at the bottom horizontal ordinate. First, as seen in Fig.4, R varies with the flow rate and the vortex frequency under all the studied flow conditions, but no obvious relationship between them is expressed. Second, the values of R in the normal condition are all greater than 80%, but R under the other three flow conditions are all less than 80%. Thus, the value greater than 80% could be used as a criterion for R to identify the normal flow condition. Third, the values of R under the pulsating, bubbly and unsteady bubbly conditions scatter in a wide range from 20%-80% and overlapped each other, so it is difficult to identify one of the three flow conditions from the other two. But on the other hand, the values of R of those three conditions are all away from those under the normal condition.

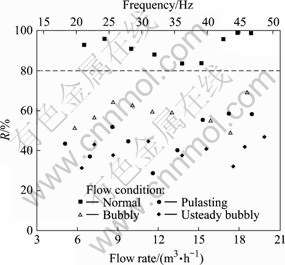
Fig.4 Distribution of vortex energy ratio under various flow conditions

These results imply that R is sensitive to the flow condition, and even small perturbation which makes the flow slightly away from the normal condition will cause significant variation to the value of R. Therefore, it is logical to adopt R as a characteristic parameter for diagnosis of the state of the vortex flowmeter. A set of feasible steps for this diagnosis are proposed as follows.

(1) Acquire the raw sensor signal of vortex flowmeter.

(2) Apply EMD to the signal and get the corresponding IMFs.

(3) Compute the energy of all IMFs.

(4) Compute the value of R.

(5) Diagnose whether the vortex flowmeter operates under the normal flow condition: if R is greater than 80%, then the condition is normal and very little or even no perturbation is imposed on the flow.

4 Conclusions

(1) Raw sensor signals of vortex flowmeter are decomposed into different IMFs using the EMD approach. The energy of each IMF is computed, and the vortex energy ratio is obtained.

(2) Simulation results show that the value of R keep nearly invariant before and after the signal is processed by the EMD. Due to this property, R is ideal to be adopted as a parameter for characterization of vortex flowmeter signals, and can be used to investigate how the perturbation in the flow affects the measurement of vortex flowmeter.

(3) Experimental results further reveal that R is sensitive to the flow condition, and even small perturbation that makes the flow slightly away from the normal condition will cause a significant variation to R. It is also found that the value of R for the normal flow condition is greater than 80% in this work, which can be employed to diagnose the state of a vortex flowmeter.

(4) The technique proposed is especially suitable for the sensor diagnosis, in which the current sensor data are used to infer whether the current measurement values are reliable. Obviously, this diagnosis approach raised may be applicable to other existing pulse-output-signal flowmeters, such as the turbine and the positive displacement flowmeter, because the method concerns only the pulse-output signal regardless of the signal source.

References

[1] TAVOULARIS S. Measurement in fluid mechanics [M]. New York: Cambridge University Press, 2005.

[2] PANKANIN G L. The vortex flowmeter: various methods of investigating phenomena [J]. Measurement Science and Technology, 2005, 16(3): R1-R16.

[3] WAKUI H, WADA M, YOSHIOKA T, ANDOH T. “DigitalYEWFLO multivariable type” vortex flowmeter with built-in temperature sensor [R]. Yokogawa Technical Report, 2004: 21-24.

[4] AMADI-ECHENDU J E, ZHU H. Signal analysis applied to vortex flowmeter [J]. IEEE Transactions on Instrumentation and Measurement, 1992, 41(6): 1001-1004.

[5] ROSSBERG A G, BARTHOLOME K, TIMMER J. Data-driven optimal filtering for phase and frequency of noisy oscillations: application to vortex flow metering [J]. Physical Review E, 2004, 69(1/2): 16216/1-16216/11.

[6] GHAOUD T, CLARKE D W. Modeling and tracking a vortex flow-meter signal [J]. Flow Measurement and Instrumentation, 2002, 13(3): 103-117.

[7] BERA S C, RAY J K, CHATTOPADHYAY S. A modified inductive pick-up type technique of measurement in a vortex flowmeter [J]. Measurement, 2004, 35(1): 19-24.

[8] HANS V, POPPEN G, von LAVANTE E, PERPEET S. Vortex shedding flowmeters and ultrasound detection: signal processing and influence of bluff body geometry [J]. Flow Measurement and Instrumentation, 1998, 9(2): 79-82.

[9] von LAVANTE E, PERPEET S, HANS V, POPPENG. Optimization of acoustic signals in a vortex-shedding flowmeter using numerical simulation [J]. International Journal of Heat and Fluid Flow, 1999, 20(4): 402-404.

[10] IGARASHI T. Resistance and Strouhal number of a vortex shedder in a circular pipe [J]. JSME International Journal Series B, 1999, 42(4): 586-595.

[11] ROSSBERG A G, RIEGLER P, BUHL F, HERWIGC J, TIMMERA J. Detection of improper installation from the sensor signal of vortex flowmeters [J]. Flow Measurement and Instrumentation, 2004, 15(1): 29-35.

[12] MIAU J J, HU C C, CHOU J H. Response of a vortex flowmeter to impulsive vibrations [J]. Flow Measurement and Instrumentation, 2000, 11(1): 41-49.

[13] MIAU J J, WU C W, HU C C, CHOU J H. A study on signal quality of a vortex flowmeter downstream of two elbows out-of-plane [J]. Flow Measurement and Instrumentation, 2002, 13(3): 75-85.

[14] HUANG N E, SHEN Z, LONG S R, WUMC, SHIHHH, ZHENGQ, YENN C, TUNGC C, LIUHH. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis [J]. Proceedings of Royal Society London Series A, 1998, 454: 903-995.

[15] WU Z H, HUANG N E. A study of the characteristics of white noise using the empirical mode decomposition method [J]. Proceedings of Royal Society London Series A, 2004, 460: 1597-1611.

[16] FLANDRIN P, RILLING G, GONCALVES P. Empirical mode decomposition as a filter bank [J]. IEEE Signal Processing Letters, 2004, 11(2): 112-114.

[17] SUN Zhi-qiang, ZHOU Jie-min, ZHOU Ping. Application of Hilbert-Huang transform to denoising in vortex flowmeter [J]. Journal of Central South University of Technology, 2006, 13(5): 501-505.

[18] SUN Zhi-qiang, ZHANG Hong-jian, ZHOU Jie-min. Investigation of the pressure probe properties as the sensor in the vortex flowmeter [J]. Sensors and Actuators: A. Physical, 2007, 136(2): 646-655.

[19] SUN Zhi-qiang, ZHANG Hong-jian, ZHOU Jie-min. Evaluation of uncertainty in a vortex flowmeter measurement [J]. Measurement, 2008, 41(4): 349-356.

Foundation item: Project(200801346) supported by the China Postdoctoral Science Foundation; Project(2008RS4022) supported by the Hunan Postdoctoral Scientific Program; Project(2008) supported by the Postdoctoral Science Foundation of Central South University

Received date: 2008-12-02; Accepted date: 2008-12-08

Corresponding author: SUN Zhi-qiang, Postdoctor, Associate professor; Tel: +86­­-731-8879863; E-mail: zqsun@mail.csu.edu.cn

(Edited by CHEN Wei-ping)