基于尺度空间理论的Harris角点检测
陈白帆, 蔡自兴
(中南大学 信息科学与工程学院, 湖南 长沙, 410083)
摘要: 研究了一种基于尺度空间理论的Harris角点检测方法。 建立Harris函数的尺度空间表示, 检测每个尺度水平上的极值, 利用迭代算法验证每个尺度水平上LoG算子是否获得最大值, 从而得到特征角点的位置及其尺度。 该方法在保持Harris角点不受光照条件及摄像机姿态变化影响的同时, 还能检测出多尺度下的特征点。 通过实验验证该方法具有尺度不变特性, 适用于尺度变化较大的视觉系统。
关键词: Harris角点; 尺度空间; LoG算子; 尺度不变性
中图分类号:TP391.41 文献标识码:A 文章编号: 1672-7207(2005)05-0751-04
Harris corner detection based on theory of scale-space
CHEN Bai-fan, CAI Zi-xing
(School of Information Science and Engineering, Central South University, Changsha 410083, China)
Abstract: An improved method of Harris corner based on the theory of scale-space was described, and a scale-space representation of Harris corner by which local maximum points were detected at each scale level was established. The extrema over scale of the Laplacian of Gaussian (LoG) which was used to select the scale of interest points were applied. For each point, an iterative algorithm can be used to detect the location and the scale of interest points simultaneously. This method not only maintains the advantages of Harris corner which is invariant to the changes of intensity and camera pose but also can be used in multi-scale. It is proved to be scale invariant by experiments and can be applied to the vision system with significant scale changes.
Key words: Harris corner; scale-space; Laplacian of Gaussian operator; scale invariant
特征点检测是机器视觉的一个重要研究内容, 大多数视觉处理任务, 如摄像机标定、 目标检测、 三维重建等, 都是基于特征点的提取, 且特征点提取的精度及质量好坏直接影响到这些处理的结果。 目前, 特征点、 角点提取方法有: 基于轮廓的方法[1, 2], 基于亮度的方法[3, 4]和基于参数模型[5, 6]的方法。
C.Schmid等[7]报道, Harris角点提取方法是目前效果最好的, 它不受摄像机姿态及光照的影响。 然而, 对于尺度变化较大的视觉系统, 该方法却不能保持特征的不变性, 如移动机器人视觉系统, 由于移动机器人位置变化, 其采集的图像不仅会有光照、 位置的变化, 还存在尺度变化。 实际图像中的特征角点常常发生在不同的尺度范围上, 并且每一角点的尺度信息是未知的。 一般认为在较大尺度下能较可靠地消除误检和检测到真正的角点, 但角点的定位不易准确。 相反, 在较小尺度下对真正的特征角点的定位比较准确, 但误检的比例会增加。 所以, 可考虑先在较大尺度下检测出角点, 然后在较小尺度下对真正特征角点进行较精确定位。
因此, 利用多尺度技术检测角点是获得理想特征角点的一种理想途径, 即有效组合利用多个不同尺度的角点检测算子, 同时正确地检测一幅图像内发生在各个尺度水平上的角点。
在此, 作者研究一种将尺度空间理论与Harris角点检测算子相结合的多尺度角点检测方法。 该方法将Harris角点函数转换为尺度空间表示形式, 并利用LoG算子来选择尺度, 最后得到特征点的位置和尺度。
1 尺度空间理论
尺度空间理论[8]是通过对原始图像进行尺度变换, 获得图像多尺度下的尺度空间表示序列, 对这些序列进行尺度空间主轮廓的提取, 并以该主轮廓作为一种特征向量, 实现边缘、 角点检测和不同分辨率上的特征提取等。
尺度空间表示是一种基于区域而不是基于边缘的表达, 作为尺度空间理论中的一个重要概念, 尺度空间核被定义为:
fout=K*fin。(1)
对于所有的信号fin, 若它与变换核K卷积后得到的信号fout中的极值(一阶微分过零点数)不超过原图像的极值, 则称K为尺度空间核, 所进行的卷积变换称为尺度变换。
尺度空间表示通过平滑获得, 可描述为(x, σ)空间, x和σ分别为位置参数和尺度参数。 当采用不同尺度的平滑函数对同一图像进行滤波时, 得到的一簇图像就是原始图像相对于该平滑函数的尺度空间, σ为尺度空间坐标。
在高斯尺度空间, 同一类型特征点和边缘在不同的尺度上具有因果性, 即当尺度变化时, 新的特征点可能出现, 而老的特征点可能移位或消失。 这种因果性带来的含糊性是固有的, 不可避免的, 不能企求消除, 但可以减小。 然而, 由于高斯核[9]

具有线性、 平移不变性、 旋转不变性和子集特性等特性, 可以证明, 高斯核是实现尺度变换的唯一变换核[10]。 因此, 利用高斯核的一阶导数将Harris角点算子变换成尺度空间的表示。
2 多尺度变换下的Harris角点算法
2.1 Harris算子的尺度空间表示
Harris算子是C.Harris和M.Stephens[3]提出的一种基于信号的点特征提取算子, 其原理为: 如果某一点向任一方向小小偏移都会引起灰度的很大变化, 这就说明该点是角点。
Harris算子R为:
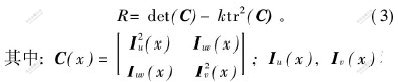
和Iuv(x)分别为图像点x的灰度在u和v方向的偏导以及二阶混合偏导; k为经验值, 通常取0.04~0.06。 当某点的Harris算子R大于设定阈值T时, 该点为角点。
Harris算子是一种有效的点特征提取算子, 其优点有:
a. 计算简单。 Harris算子中只用到灰度的一阶差分, 操作简单。
b. 提取的点特征均匀而且合理。 Harris算子对图像中的每个点都计算其兴趣值, 然后在邻域中选择最优点。 实验表明, 在纹理信息丰富的区域, Harris算子可以提取出大量有用的特征点, 而在纹理信息少的区域, 提取的特征点则较少。
c. 可定量的提取特征角点。
d. 即使存在有图像的旋转、 灰度的变化、 噪音影响和视点的变换, 它也是最稳定的一种点特征提取算法[11]。
然而, Harris算子并不具有尺度不变性。 因此, 作者提出结合尺度空间理论来改进Harris算子。
为了获取Harris算子的尺度空间表示, 首先计算图像上某点x在u和v方向上的偏导, 然后与标准偏差为sσn(其中: s为一常量, s>1)的高斯核的微分进行卷积:
Iu(x, sσn)=I(x)*Gu(x, sσn);(4)
Iv(x, sσn)=I(x)*Gv(x, sσn)。(5)
则Harris角点中C(x)的函数将变为

其中: σI=σn, 为计算特征点时选择的尺度参数; σD=sσn, 为微分尺度; G(σI)为高斯函数。
通过判断
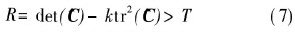
即可检测出σn尺度水平上的特征角点。
假设某一角点如图1(a)所示, 则该角点尺度空间表达如图1(b)所示。
2.2 多尺度角点检测算法
LoG算子2g, 是由D.Marr和E.Hildreth提出的, 又称Marr-Hildreth算子。
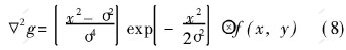
其中: f(x, y)为待检测函数。

图 1 尺度空间下的Harris角点
Fig. 1 Harris Corner in scale-space
LoG算子将高斯滤波和拉普拉斯边缘检测结合在一起, 主要用于边缘检测。 在本文中, 采用一个典型的LoG算子模板, 验证某一指定的尺度水平上检测出的角点是否为极值, 从而得到具尺度不变性的特征角点。
多尺度Harris角点检测算法的具体步骤如下:
a. 预选尺度变量σn及阈值T, 利用式(6)和(7)计算出每一尺度水平上的候选特征角点。 b. 利用迭代算法验证每个尺度水平上的候选角点的LoG算子是否获得最大值, 从而得到最终特征角点的位置与尺度。 考虑图像的整个尺度空间, 假设在大尺度水平σn=σ0上检测到的角点集Copt, 将图像尺度坐标减小为σn=σ1, 对于该图像在Copt的邻域内检测新的角点集Cnew, 若存在Cnew, 则接受Cnew为当前图像特征角点集。 重复以上过程, 直至Cnew不再变化, 或图像尺度足够小为止。
3 实验结果与分析
实验中, 取高斯核函数的标准偏差比例常量s=0.7(这是由多次实验得出的经验值, 可根据图像中检测目标不同进行调整), Harris角点算子中的常量k=0.04, 阈值T=1000, 且采用一个典型的5×5的LoG算子模板:

当σn分别取3, 2和1时, 初始图像的角点提取结果如图2(b), 2(c)和2(d)所示。

图 2 3种尺度下的Harris角点检测
Fig. 2 Harris corner detection at three scales
可以看出, 对于黑白方格这样的简单目标, 用尺度σn=3即可提取出有用的特征角点, 但对于比较复杂的目标, 如图中的除黑白方格以外的目标, 则需要更小的尺度。
某一角点检测算法的优劣可通过稳定性准则、 可靠性准则和抗噪性能准则来评价[12]。 这3个准则依靠改变参数、 阈值或增加噪声后检测出的角点与初始检测出的角点的重复率η决定。

其中: Ci表示检测到的特征角点集合; |Ci|表示集合Ci中元素的数目; min代表取2个数中的较小者; 分子的含义是计算不同尺度下检测到的完全相同的角点(即横、 纵坐标都相同)的数目。 由式(9)可知, 重复率η越大, 算法的稳定性越高。
利用重复率η来检验该基于尺度空间理论的Harris角点检测算法的稳定性和可靠性。 对图2中的初始图像进行不同尺度下的角点检测(σn∈[1, 4.5]), 则C1和C2分别表示算法在第一个尺度和第二个尺度中检测到的角点的集合, 计算其重复率。 并将其与未改进的Harris角点的稳定性进行比较, 结果如图3所示。
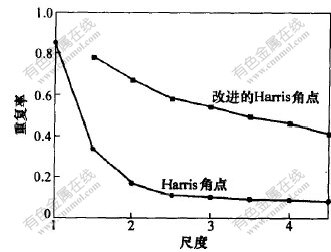
图 3 2种Harris角点的重复率比较
Fig. 3 Comparison of repeatability rate of original and improved Harris corner
由图3可以看出, 当尺度变化时, 该基于尺度空间理论的Harris角点检测方法比原Harris角点检测更稳定和可靠, 即更具尺度不变性。
4 结 论
a. 利用尺度空间理论将Harris角点函数变换成尺度空间的表示形式, 从而检测出每一尺度水平上的特征点。 然后, 利用LoG算子迭代计算出多尺度下的特征角点。
b. 该方法继承了Harris角点的不受光照、 旋转影响的优点, 并增加了尺度不变特性, 具有较强的稳定性和可靠性。
参考文献:
[1]Mokhtarian F, Suomela R. Robust image corner detection through curvature scale space[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(12): 1376-1381.
[2]Pikaz A, Dinstein I. Using simple decomposition for smoothing and feature point detection of noisy digital curves[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1994, 16(8): 808-813.
[3]Harris C, Stephens M. A combined corner and edge detector[A]. Matthews M M. Proceedings of the Fourth Alvey Vision Conference[C]. Manchester: the University of Sheffield Printing Unit, 1988. 147-151.
[4]Deriche R, Giraudon G. A computational approach for corner and vertex detection[J]. International Journal of Computer Vision, 1993, 10(2): 101-124.
[5]Baker S, Nayar S K, Murase H. Parametric feature detection[J]. International Journal of Computer Vision, 1998, 27(1): 27-50.
[6]Parida L, Geiger D, Hummel R. Junctions: Detection, classification, and reconstruction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1998, 20(7): 687-698.
[7]Schimid C, Mohr R, Bauckhage C. Evaluation of interest point detectors[J]. International Journal of Computer Vision, 2000, 37(2): 151-172.
[8]Lindeberg T. Scale-space theory: A basic tool for analysing structures at different scales[J]. Journal Applied Statistics, 1994, 21(2): 223-261.
[9]Babaud J, Witkin A P, Baudin M, et al. Uniqueness of the Gaussian kernel for scale-space filtering[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, 8(1): 26-33.
[10]吴立德. 计算机视觉[M]. 上海: 复旦大学出版社, 1993.
WU Li-de. Computer Vision[M]. Shanghai: Fudan University Press, 1993.
[11]Schmid C, Mohrand R, Bauckhage C. Comparing and evaluating interest points[A]. Ahuja N, de Sai U. Proceedings of the Sixth International Conference on Computer Vision[C]. Washington: IEEE Computer Society, 1998. 230-235.
[12]杨杨, 张田文. 角点检测算法评价方法的研究[J]. 哈尔滨工业大学学报, 1998, 30(2): 7-10.
YANG Yang, ZHANG Tian-wen. Assessing criterion of corner finders[J]. Journal of Harbin Institute of Technology, 1998, 30(2): 7-10.
收稿日期:2005-01-28
基金项目:国家自然科学基金资助项目(60234030)
作者简介:陈白帆(1979-), 女, 湖南常德人, 博士研究生, 从事机器视觉研究
论文联系人: 陈白帆, 女, 博士研究生; 电话: 0731-8830583(O); E-mail: chenbaifan@21cn.com