Analytical solution of vacuum preloading technology combined with electroosmosis coupling considering impacts of distribution of soil’s electrical potential
来源期刊:中南大学学报(英文版)2021年第8期
论文作者:沈扬 冯建挺 许俊红 施文
文章页码:2544 - 2555
Key words:vacuum preloading-electroosmosis; non-linear distribution; 2D plane strain; coupling consolidation model; pore water pressure
Abstract: Combining vacuum preloading technology and electroosmosis can improve the treatment effect of soft soil foundation by utilizing the advantages of both methods. Many studies indicate that the soil electrical potential is non-linearly distributed in the treatment process by the combined method. However, in the previous theoretical study, the non-linear-distribution impacts of soil’s electrical potential on soft soil foundation treatment have not been considered. It is always assumed to be linear distribution, which is different from the experimental results. In this paper, the coupling consolidation model of this technology under the two-dimensional plane strain condition is initially established; and the well resistance effect, the vacuum load decreasing along the soil depth and the non-linear variation of electrical potential in the soil are considered. Then, the analytical solutions of the average excess pore water pressure and soil’s consolidation degree in the anode affected area are acquired based on the soil’s electrical potential distribution. Finally, the rationality of the analytical solution is testified by conducting an experimental model test, which proves the scientificity of the analytical solution. The analytical solution is adopted to better predict the dissipation of excess pore water pressure and soil consolidation degree when using the combined technology. This study can provide a reference with more accuracy for the engineering practices of this combined technology in the future.
Cite this article as: FENG Jian-ting, SHEN Yang, XU Jun-hong, SHI Wen. Analytical solution of vacuum preloading technology combined with electroosmosis coupling considering impacts of distribution of soil’s electrical potential [J]. Journal of Central South University, 2021, 28(8): 2544-2555. DOI: https://doi.org/10.1007/s11771-021-4785-8.

J. Cent. South Univ. (2021) 28: 2544-2555
DOI: https://doi.org/10.1007/s11771-021-4785-8
FENG Jian-ting(冯建挺)1, 2, SHEN Yang(沈扬)1, XU Jun-hong(许俊红)3, SHI Wen(施文)1
1. Key Laboratory of Ministry of Education for Geomechanics and Embankment Engineering,Hohai University, Nanjing 210024, China;
2. School of Civil Engineering, University of Leeds, Leeds, LS2 9JT, UK;
3. College of Civil Engineering, Nanjing Forestry University, Nanjing 210037, China
 Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Central South University Press and Springer-Verlag GmbH Germany, part of Springer Nature 2021
Abstract: Combining vacuum preloading technology and electroosmosis can improve the treatment effect of soft soil foundation by utilizing the advantages of both methods. Many studies indicate that the soil electrical potential is non-linearly distributed in the treatment process by the combined method. However, in the previous theoretical study, the non-linear-distribution impacts of soil’s electrical potential on soft soil foundation treatment have not been considered. It is always assumed to be linear distribution, which is different from the experimental results. In this paper, the coupling consolidation model of this technology under the two-dimensional plane strain condition is initially established; and the well resistance effect, the vacuum load decreasing along the soil depth and the non-linear variation of electrical potential in the soil are considered. Then, the analytical solutions of the average excess pore water pressure and soil’s consolidation degree in the anode affected area are acquired based on the soil’s electrical potential distribution. Finally, the rationality of the analytical solution is testified by conducting an experimental model test, which proves the scientificity of the analytical solution. The analytical solution is adopted to better predict the dissipation of excess pore water pressure and soil consolidation degree when using the combined technology. This study can provide a reference with more accuracy for the engineering practices of this combined technology in the future.
Key words: vacuum preloading-electroosmosis; non-linear distribution; 2D plane strain; coupling consolidation model; pore water pressure
Cite this article as: FENG Jian-ting, SHEN Yang, XU Jun-hong, SHI Wen. Analytical solution of vacuum preloading technology combined with electroosmosis coupling considering impacts of distribution of soil’s electrical potential [J]. Journal of Central South University, 2021, 28(8): 2544-2555. DOI: https://doi.org/10.1007/s11771-021-4785-8.
1 Introduction
Soft soil layers with higher water content, higher compressibility, lower permeability, lower strength and higher liquid limit are widely distributed in China’s coastal and river areas [1]. These characteristics can strongly affect the stability and safety of the buildings and structures built there, resulting in serious engineering safety accidents due to excessive foundation settlement or settlement difference when the construction is placed directly on the foundation formed by the soft soil layer, threatening people’s lives and property. Therefore, it is necessary to pre-consolidate the soft soil foundation and to meet the requirements for concrete engineering application.
Vacuum preloading technology is usually used to reinforce the soft soil foundation due to its low cost, simple and green operation, and reduced pollution [2-9]. Vacuum preloading has been used successfully to treat large tidal-flat areas in Tianjin, Guangzhou, Shenzhen and other coastal parts of China. However, this method has some engineering problems to be addressed, such as the severe loss of vacuum transmission along the drainage plate, the less satisfactory reinforcement effect of the soil bottom, the long reinforcement period caused by the blockage of the drainage plate, the uneven reinforcement effect and the visible settlement after the completion of construction [10-13]. In the attempt to solve these problems, many researchers have been actively engaged in related studies.
Recently, the electroosmotic method has attracted extensive attention in academic and engineering circles with the breakthrough made by researchers in the field of electro-kinetic geosynthetics (EKG) [13-17]. In comparison with vacuum preloading, the electroosmotic method has the advantage of being able to treat dredger fill silt with a higher content of fine particles, lower bearing capacity, lower permeability, higher water content and higher compressibility than the vacuum preloading method [18-22]. However, electroosmosis has many problems that need to be addressed, such as serious corrosion of the anode electrode, the uneven soil reinforcement effect, the unsatisfactory treatment effect of soil near the cathode, large energy consumption, and low electroosmosis efficiency in the late period of treatment [23-27]. These problems have seriously restricted the practical application of the electroosmotic method.
Meanwhile, with the rapid development of dredging projects and reclamation epeirogenic engineering in China, the need for the building on soft soil is increasing [28, 29]. The problem of how to quickly and efficiently improve the bearing capacity of the soft soil foundation has become urgent. To address this issue, some scholars have proposed that the technologies of vacuum preloading and the electroosmosis can be combined to produce better results, which is named vacuum preloading-electroosmosis (VPE). Some researchers have conducted experimental studies on this joint reinforcement technology, proving that VPE method can improve the effect of the treatment of soft soil foundation by utilizing the advantages of both methods [28-37].
Additionally, related research on the theory of vacuum preloading-electroosmosis method has also been explored. Based on theories on the varied mode of consolidation brought by ESRIG [38], XU et al [39] developed a two-dimensional consolidation equation on soft soil foundation that was strengthened by the combined technology. The analytical expression of excess pore water pressure (EPWP) during the conducting process of combined method was given and the rationality of the theoretical solution was also verified by the model test in the laboratory. Based on the assumption of equal strain, WU et al [40] simplified the quincunx arrangement of electrodes, making it an axisymmetric problem, deriving the analytical solution of the one-dimensional consolidation model of this combined method under the axisymmetric condition. Meanwhile, related finite element software was introduced to simulate the consolidation of soft soil foundation to explore the EPWP and the process of soil consolidation under three varied reinforcement technologies: vacuum preloading, electroosmosis and vacuum preloading combined with electroosmosis. WANG et al [41] took advantage of the exponential function to describe the attenuation of voltage with time in electroosmosis and established a two-dimensional consolidation theory on the drainage of VPE technology considering the horizontal and vertical directions. The analytical solution of the EPWP and the calculation equation of average consolidation degree were given, and the numerical solutions were compared and verified with the analytical solution. WANG et al [31] also proposed an analysis model named electroosmosis-vacuum preloading-surcharge preloading, which comprehensively evaluates the non-linear changes of compressibility, permeability and electroosmotic permeability with the void ratio. The rationality of this analytical model was verified by experimental results.
However, it was found that the distribution of soil voltage was assumed to be linear in the above theoretical or numerical studies, including many existing theories of electroosmotic consolidation. The soil voltage varied from the results of laboratory tests in recent years [42]. Based on the existing research, it was discovered that the electrical potential in soil will jump near the anode and cathode in the VPE method. Such a situation is caused mainly by the contact resistance between the electrode and the soil. Therefore, in the theoretical derivation, it is unreasonable to assume a linear distribution of soil’s electrical potential.
In order to reflect the soil consolidation in the VPE method in a more reasonable way, the coupling consolidation model of this combined technology is established (with the anode electrode as the research object) based on the law of determined nonlinear distribution of soil’s electrical potential. The EPWP’s analytical solutions and the soil’s consolidation degree of the VPE technology at varied positions (within the influence range of the anode) can be reached based on the theoretical derivation of the two-dimensional plane strain condition. Finally, the theoretical solution can be verified by applying the model test case to provide a reference with a better theoretical basis for the subsequent application of VPE method.
2 Establishment of consolidation equation for combined method
2.1 Mathematical model
Based on the rectangular arrangement of the anode and the cathode, when electroosmosis is introduced to treat the soft soil foundation in the practical engineering process, a vertical two-dimensional plane model with the anode electrode as the object can be established as shown in Figure 1. dQx is the flow in the x direction of the drain from the entrance to the exit; Qz is the total change in flow from the entrance face to the exit face; dz is the height of the study zone; u and us are the pore water pressure of the non-smear and smear zone, respectively; b is influence radius of the drainage body; bs is the radius of the smear zone; bw is the simplified radius width of the drainage body.
In this model, each electrode will be shared by two elements, i.e., one anode and one cathode are introduced to treat the soil within a basic unit area within the soil (see Figure 2).
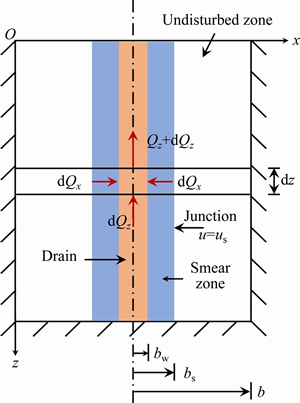
Figure 1 Calculation diagram of VPE under 2D plane strain
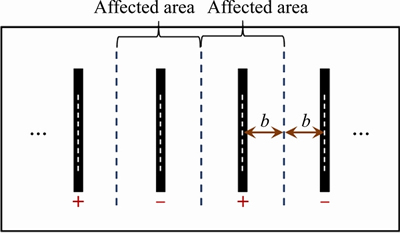
Figure 2 Layout of drainage body under 2D plane strain conditions
The rectangular coordinate system xOz is then established in the mathematical model. Compared with the axisymmetric simplified consolidation model, the drainage plate can be simplified as a rectangular vertical drainage plate with a width of 2bw. A voltage difference of U will be formed in the soil area to be reinforced when the cathode and anode electrodes are connected to the DC power supply at the same time. The negative pressure of -p0 is formed on the surface of the soil by vacuum loading. The hydraulic permeability coefficient (undisturbed zone) is set as kh and the electric permeability coefficient is set as ke.
The theoretical derivation of this paper originates from the novel electrode material, namely the new EKG material. And its structure diagram is also displayed in Figure 3.
The shape of the new tabular EKG is similar to that of the plastic drainage board used in vacuum preloading. It contains a geomembrane, substrate and wires. The substrate is made of conductive plastic. Both sides of the substrate are covered with grooves for drainage. Two copper wires, which are connected to the power supply, are embedded in the substrate. Compared with the former EKG material, the new one presents better drainage capacity and conductivity considering the improvement of manufacturing process, which is beneficial for coupling of vacuum preloading and electroosmosis [26]. And unlike the traditional metal electrode, the EKG electrode can shorten the consolidation time, prevent electrode corrosion and also increase the coupling of the electroosmotic flow field and hydraulic seepage field [43, 44].
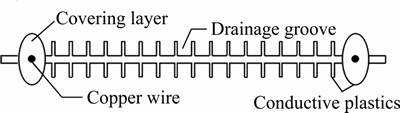
Figure 3 Schematic diagram of tabular EKG
Taking the projects into consideration, a horizontal smear zone with the midpoint of the EKG electrode as the center and with its width at 2bs will be formed during the treatment of combined reinforcement, as shown in Figure 1. The hydraulic permeability coefficient of this area is less than kh, which is assumed to be ks [45, 46]. Additionally, radial seepage with the EKG drainage body as its center will be formed under vacuum loading when reinforcing the soft foundation. The width of the vertical drainage body in the affected area is 2b. Water flow from the anode to the cathode can be formed when electroosmosis is applied to reinforce the soft soil foundation. Therefore, areas for mutual inhibition and mutual promotion can be formed at the same time when vacuum preloading and electroosmosis are coupled. The difference between them is reflected in the addition and subtraction of the hydraulic seepage rate and the electroosmotic flow rate.
2.2 Basic assumptions
Considering that the treatments for the soft soil foundation applied in this paper are complex and the coupling effect of multiple physical fields may be involved, the following basic assumptions are adopted in the establishment of the drainage consolidation equation to better conduct relevant theoretical derivations.
1) Only the horizontal seepage is considered, and the vertical seepage can be ignored. Both sides of the boundary are closed. Darcy’s law is adopted to describe the flow of pore water. The flow led by difference in voltage and water head can be superimposed on each other.
2) The soil is saturated and homogeneous. The compression of soil particles and water is so light that it can be neglected. The amount of water discharged from the soil unit within unit time is equal to the compression volume of the soil mass.
3) The equal strain condition is applicable. Without considering the lateral deformation of the soil, the vertical strain of the soil at the same depth can be equal. The hydraulic permeability coefficient and the electric permeability coefficient of the soil do not change during the process of soil consolidation.
4) There is a reduction effect of vacuum loading along the depth direction of the drain board. Assuming that the vacuum pressure on the upper surface of the soil is -p0 and at the bottom of the drainage plate is -k1p0 (k1 is the vacuum transfer coefficient, 0
2.3 Theoretical basis
The coupling of the VPE method involves the superposition of hydraulic seepage and electroosmotic flow, which can be calculated by adopting Mitchell’s theory of multi-field coupling:
 (1)
(1)
 (2)
(2)
where Ji is the flow rate or velocity of each flow; Xi is the driving force corresponding to each flow; Lii is the conductivity coefficient; Lij is the coupling coefficient. There is a linear relationship between Ji and Xi according to Eq. (1). It can be found that one type of driving force Xj in the soil can give rise to another type of water flow Ji according to Eq. (2).
Therefore, the discharge rate of the water flow generated by the combined action of vacuum preloading and electroosmosis at the anode and cathode can be explained as the superposition of the water flow velocity caused by the hydraulic gradient and the voltage gradient, which is described as follows:
At the anode,
 (3)
(3)
At the cathode,
 (4)
(4)
where v is the flow velocity; ih is the hydraulic gradient and ie is the voltage gradient.
In addition, according to the distribution law of soil voltage, which was determined by several previous laboratory tests (see Figure 4), the expression of soil voltage at varied positions can be described as follows [42]:
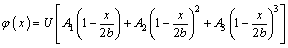 (5)
(5)
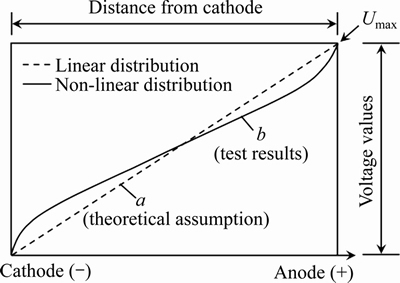
Figure 4 Diagram of soil voltage distribution
In the anode influence area, x≤b. It can be further induced that:
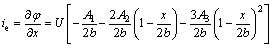 (6)
(6)
where x is the distance from the anode; 2b is the distance between the cathode and anode; U is the external applied voltage; A1, A2 and A3 are the coefficients closely related to the applied external voltage, and the values can be directly obtained from the voltage value. The relevant calculation equation is as follows:
 (7)
(7)
2.4 Consolidation equation
The theoretical derivation is obtained by taking the drainage body in the anode affected area as an
example. It can be seen from Eq. (3) that the flow into the vertical drainage plate at the anode is formed by the coupling of the hydraulic seepage and electroosmotic flow:
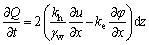 (8)
(8)
where Q is the quantity of the flow; u is the EPWP formed under the combined technology; γw is the gravity of the water; and φ is the soil voltage.
According to Eq. (2), the water discharged from the soil is equal to the volume compression of the soil mass. The vertical volume change rate of the soil is as follows:
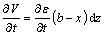 (9)
(9)
Furthermore,
 (10)
(10)
Equation (10) can be further transformed into:
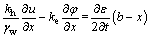 (11)
(11)
The following equation can be obtained after simplification:
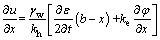 (12)
(12)
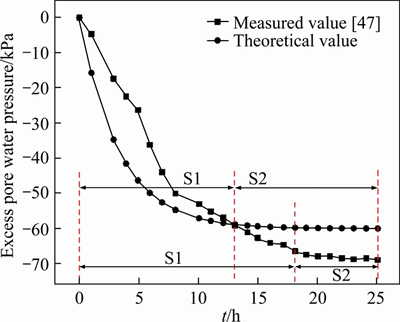
In the above equation, bs By transforming Eq. (12), the gradient of excess pore water pressure in the smear zone (bw≤x≤bs) can be described as follows: where us is the EPWP in the smear zone; and ks is the hydraulic permeability coefficient of the smear zone. Additionally, according to the calculation model shown in Figure 1, the actual width of the drainage plate is 2bw at time t during the process of drainage. For a drainpipe with a height of dz, the volume of flow coming from the bottom is Qz, and the volume of water flowing from the top is (Qz+dQz). Then, during the time period dt, the change of water volume in the drainage body of this section is as follows: where qw is the discharge capacity of the drainage body, x≤bw. When x=bw, the quantity of flow (dQx) on each side of the inflow interface is as follows: The following equation can be obtained according to the principle of flow continuity: Therefore, It can be further transformed into the following equation: Since there is no sudden change of EPWP on the drainage boundary of x=bw, here it is u=us. Meanwhile, the quadratic function of EPWP along the depth direction on x=bw can be calculated by substituting Eq. (13) into Eq. (18): According to the engineering conditions, the boundary conditions of the model can be obtained as follows: z=0, z=l, By integrating Eq. (19), the following equation can be obtained: Further integration may give rise to the following equation: According to the boundary conditions, the expressions of C1 and C2 can be easily obtained as follows: In addition, according to Eq. (13), the EPWP at any position of the smear zone can be integrated as follows: The expressions of C3 can be obtained according to the value of EPWP obtained at x=bw: The EPWP at any position in the undisturbed zone can be obtained after integrating Eq. (12): When x=bs, i.e., at the junction of the smear zone and the non-smear zone, there is no sudden change of EPWP. Here it is u=us. Therefore, the expression of C4 can be obtained: The average EPWP at depth z and time t can be obtained from Eqs. (22) and (23): In addition, the following equation can be obtained according to the continuity condition of seepage. where mv is the coefficient of volume compressibility. Combined with Eqs. (22)-(25), the following equation can be obtained after further calculation and simplification: where The radial consolidation degree at any depth can be deduced from following equation: where u0 is the initial EPWP and 3 Analytical solution validation The drainage consolidation equation of the VPE technology is derived according to the distribution law of the electrical potential in soil. The rationality of the equation will be verified by the specific test case. When integrating the relevant published experimental research results, it was found that SUN et al had carried out a laboratory test on VPE method in 2018 [47]. The test data are complete, and can be adopted to analyze and verify the drainage consolidation equation. The test sample of soil was taken from the dredger fill foundation site of an island in Ezhou, Hubei Province, China, which was a typical muddy clay. The basic physical and mechanical parameters of the sample could be obtained in the laboratory test. The following parameters were mainly selected according to the analytical expression as shown in Table 1. Table 1 Main test parameters The above-mentioned parameters are directly quoted from the article [47]. In addition, considering the applied voltage was 50 V, according to Eq. (7), it can be calculated that A1=-2.1078, A2=9.791, A3=-6.822. The laboratory test of the combined method took 25 h in total. By substituting the above parameters into Eq. (26), the dissipation of EPWP within the affected range of anode under the condition of non-linear soil voltage distribution can be obtained. The EPWP measured by the laboratory test and calculated by the theoretical analytical expression is plotted in Figure 5. Figure 5 Dissipation of EPWP Figure 5 illustrates that the measured value of EPWP correlates well to the theoretical value, which indicates that the rationality of the proposed equation. Besides, it can be seen that both of the values are less than 82 kPa, which is mainly caused by the attenuation of the vacuum loading along the soil depth [43]. Figure 5 also indicates that the theoretical value of EPWP is larger than the measured value for a long time under the force of VPE, which is mainly attributed to the change of voltage [44]. Many studies reveal that the voltage decreases gradually with time in the process of electroosmosis or VPE treatment. However, it is not considered in the theoretical derivation. The voltage is assumed to be a constant value and it does not change with time. Although the variation trend of EPWP, whether it is calculated value or measured value, can be divided into two stages: S1 (EPWP changes obviously) and S2 (EPWP changes slightly), Figure 5 also reveals that there are some differences between the theoretical value and the measured value. The theoretical value first reaches the S2 stage before the measured value. The difference between the theoretical value and the measured value can be the result of the adoption of the equal strain assumption in the theoretical derivation. It was assumed that the vertical strain of the soil inside and outside the smear zone was equal. However, the settlement at the cathode and anode can be different in the practical measurement, which serves as one of the main reasons for the difference. As for the theoretical calculation of EPWP reaching the S2 status earlier, it is considered to result from the fact that soil in the affected area around the anode tends to be associated with a more violent chemical reaction and the effect of electrolytic heat release, which may affect the dissipation of EPWP. The impacts can be gradually weakened, while the pore water pressure changes caused by electrolytic heat release and chemical reaction were not taken into consideration in the theoretical derivation. Meanwhile, it also explains the difference between the theoretical value and the measured value. 4 Discussion In this paper, the two-dimensional consolidation equation of the combined technology for soft foundation reinforcement is established based on the above-mentioned four assumptions. However, this method may give rise to many effects under the combined action of electrochemistry and drainage consolidation, such as electrokinetic effect, electrochemical corrosion effect, expansion densification effect and electrolytic water consumption effect [48]. The process can be simplified and approximated as a drainage consolidation, which is different from the situation of the concrete projects. Therefore, there are many issues left to be discussed. 1) The electroosmotic coefficient changes over time during testing of the combined technology. The hydraulic permeability coefficient also changes significantly due to the continuous discharge of pore water and the consolidation of soil. The variation of the permeability coefficient along with the consolidation process needs to be explored in the further study. Besides, the soil may transform into the unsaturated state in the late stage of the experiment due to the large amount of water discharged from the soil, and the physical and mechanical properties of soil may also change. These factors may cause some difference between the analytical solution and the actual value. 2) Complex chemical reactions may occur in the soil when the combined method is adopted to reinforce the soft foundation. For example, the oxidation reaction may occur at the anode, which will produce hydrogen peroxide ions and then react with high valence metal cations in the soil to generate some insoluble substances. It can be rather complicated to establish an equation considering these chemical effects. Therefore, in this study, the two-dimensional consolidation equation of the combined technology is established without considering the chemical reaction in the soil. 3) The distribution law of soil’s electrical potential adopted in this paper is obtained under the premise that the vacuum preloading method and the electroosmotic method are both implemented and completed at the same time. Additionally, only the EPWP and the soil consolidation degree in the affected area of the anode are calculated. It is only required to repeat the above derivation steps according to Eq. (4), if it’s necessary to calculate the EPWP and soil consolidation degree in the cathode affected area. 4) Concerning the direct discharge test at the cathode: when compared with the conventional two-sided pumping test, its percolation path in the flow can be doubled. Meanwhile, when the external vacuum loading is constant, the hydraulic gradient outside the smear zone should be reduced by half, and the impact thickness of the parameter under two-dimensional plane strain should also be doubled. The variation laws of EPWP and soil consolidation degree under the two construction methods can be compared by substituting the above-mentioned parameters into the equation. 5 Conclusions In this paper, based on the actual distribution of the electrical potential in the soil and the rectangular arrangement of electrodes in vacuum preloading technology combined with electroosmosis, a vertical 2D plane drainage consolidation model of the novel EKG electrode vacuum preloading combined with the electroosmotic method was established. The dissipation equation of the average EPWP and the average degree of consolidation of the soil in the anode affected area were also derived. Finally, the rationality of the equation was verified and testified by analyzing a specific test case. The conclusions can be stated as follows: 1) The consolidation equation for the combined method was established based on the distribution law of electrical potential in soil, which helped to better reflect the consolidation of the soil. Considering that the existing consolidation theories need to be improved, the equation obtained in this study may provide a reference and guidance for the subsequent practices of this combined reinforcement technology in engineering. 2) The dissipation trend of the theoretical value of the average EPWP in the affected anode area is generally consistent with the measured value. However, there are differences between the theoretical value and the measured value. The reasons for these differences may lie in that some assumptions were adopted in this paper, and the dissipation of EPWP can be affected by chemical reaction and temperature field changes. A more convincing theoretical value would be obtained if those assumptions can be gradually adjusted or improved, or if the equations can be established considering temperature effect and ion reaction effect. Contributors FENG Jian-ting provided the concept and edited the draft of manuscript. SHEN Yang carried out data processing, performed data analysis, and contributed to the paper writing. XU Jun-hong author contributed a lot in the related work of modification and beautification of the figures, as well as polishing of the language. SHI Wen conducted the literature review. Conflict of interest FENG Jian-ting, SHEN Yang, XU Jun-hong and SHI Wen declare that they have no conflict of interest. References [1] LIU Han-long, CUI Yun-liang, SHEN Yang, DING Xuan-ming. A new method of combination of electroosmosis, vacuum and surcharge preloading for soft ground improvement [J]. China Ocean Engineering, 2014, 28(4): 511-528. DOI: 10.1007/s13344-014-0042-3. [2] TANG M, SHANG J Q. Vacuum preloading consolidation of Yaoqiang Airport runway [J]. Géotechnique, 2000, 50(6): 613-623. DOI: 10.1680/geot.2000.50.6.613. [3] CHAI J C, CARTER J P, HAYASHI S. Vacuum consolidation and its combination with embankment loading [J]. Canadian Geotechnical Journal, 2006, 43(10): 985-996. DOI: 10.1139/T06-056. [4] SAOWAPAKPIBOON J, BERGADO D T, VOOTTIPRUEX P, LAM L G, NAKAKUMA K. PVD improvement combined with surcharge and vacuum preloading including simulations [J]. Geotextiles and Geomembranes, 2011, 29(1): 74-82. DOI: 10.1016/j.geotexmem.2010.06.008. [5] KIANFAR K, INDRARATNA B, RUJIKIATKAMJORN C. Radial consolidation model incorporating the effects of vacuum preloading and non-Darcian flow [J]. Géotechnique, 2013, 63(12): 1060-1073. DOI: 10.1680/geot.12.P.163. [6] VOOTTIPRUEX P, BERGADO D T, LAM L G. Back-analyses of flow parameters of PVD improved soft Bangkok clay with and without vacuum preloading from settlement data and numerical simulations [J]. Geotextiles and Geomembranes, 2014, 42(5): 457-467. DOI: 10.1016/ j.geotexmem.2014.07.004. [7] LOPEZ-ACOSTA N P, ESPINOSA-SANTIAGO A L, PINEDA-NUNEZ V M. Performance of a test embankment on very soft clayey soil improved with drain-to-drain vacuum preloading technology [J]. Geotextiles and Geomembranes, 2019, 47(5): 618-631. DOI: 10.1016/j.geotexmem.2019. 103459. [8] LIU Fei-yu, WU Wen-qing, FU Hong-tao. Application of flocculation combined with vacuum preloading to reduce river-dredged sludge [J]. Marine Georesources & Geotechnology, 2020, 38(2): 164-173. DOI: 10.1080/ 1064119X.2018.1564092. [9] XU Gui-zhong, YIN Jie, FENG Xu-song, FENG J. An improved method for dewatering sewage sludge using intermittent vacuum loading with wheat straw as vertical drains [J]. KSCE Journal of Civil Engineering, 2020, 24(7): 2017-2025. DOI: 10.1007/s12205-020-2216-2. [10] CAI Yuan-qiang, QIAO Huan-huan, WANG Jun. Experimental tests on effect of deformed prefabricated vertical drains in dredged soil on consolidation via vacuum preloading [J]. Engineering Geology, 2017, 222: 10-19. DOI: 10.1016/j.enggeo.2017.03.020. [11] LEI Hua-yang, LU Hai-bin, LIU Jing-jin, ZHENG Gang. Experimental study of the clogging of dredger fills under vacuum preloading [J]. International Journal of Geomechanics, 2017, 17(12): 1-14. DOI: 10.1061/ (ASCE)GM.1943-5622.0001028. [12] LI Jin-feng, CHEN Hui-e, YUAN Xiao-qing, SHAN Wen-chong. Analysis of the effectiveness of the step vacuum preloading method: a case study on high clay content dredger fill in Tianjin, China [J]. Journal of Marine Science and Engineering, 2020, 8(1): 38. DOI: 10.3390/jmse8010038. [13] ZHANG Wen-gang, GOH A T C, GOH K H. Performance of braced excavation in residual soil with groundwater drawdown [J]. Underground Space, 2018, 3(2): 150-165. DOI: 10.1016/j.undsp.2018.03.002. [14] ZOU Wei-lie, YANG Jin-xing, WANG Zhao. Design methods of electro-kinetic geosynthetics for consolidation and soil reinforcement [J]. Chinese Journal of Geotechnical Engineering, 2002, 24(3): 319-322. DOI: 10.3321/j.issn: 1000-4548.2002.03.011. (in Chinese) [15] JONES C, LAMONT-BLACK J, HUNTLEY D. Electrokinetic geosynthetics: From research to hype to practice [C]// Proceedings of The Institution of Civil Engineers-Civil Engineering, 2017, 170(3): 127-134. DOI: 10.1680/jcien.16.00039. [16] GLENDINNING S, LAMONT-BLACK J, JONES C J F P, HALL J. Treatment of lagooned sewage sludge in situ using electrokinetic geosynthetics [J]. Geosynthetics International, 2008, 15(3): 192-204. DOI: 10.1680/gein.2008.15.3.192. [17] JONES C. Briefing: Electrokinetic geosynthetics: getting themost out of mud [J]. Proceedings of the Institution of Civil Engineers-Civil Engineering, 2004, 157(3): 103. DOI: 10.1680/cien.2004.157.3.103. [18] LOCKHART N C. Electroosmotic dewatering of clays. I. Influence of voltage [J]. Colloids and Surfaces, 1983, 6(3): 229-238. DOI: 10.1016/0166-6622(83)80015-8. [19] FU Hong-tao, FANG Zi-quan, WANG Jun. Experimental comparison of electroosmotic consolidation of Wenzhou dredged clay sediment using intermittent current and polarity reversal [J]. Marine Georesources & Geotechnology, 2018, 36(1): 131-138. DOI: 10.1080/1064119X.2017.1326992. [20] FLORA A, GARGANO S, LIRER S, MELE L. Experimental evidences of the strengthening of dredged sediments by electroosmotic consolidation [J]. Geotechnical and Geological Engineering, 2017, 35(6): 2879-2890. DOI: 10.1007/s10706-017-0286-9. [21] LI Ying, GONG Xiao-nan. Design method of electro-osmosis reinforcement for soft clay foundations [J]. Chinese Journal of Geotechnical Engineering, 2011, 33(6): 955-959. (in Chinese) [22] XIE Xin-yu, LIU Yi-min, ZHENG Ling-wei. Experimental study on the effect of soil saturation on the electric permeability coefficient during electroosmosis process [J]. Marine Georesources & Geotechnology, 2019, 37(10): 1188-1195. DOI: 10.1080/1064119X.2018.1540673. [23] HU Jian-li, LI Xiao-bing, ZHANG Di-kang. Experimental study on the effect of additives on drainage consolidation in vacuum preloading combined with electroosmosis [J]. KSCE Journal of Civil Engineering, 2020, 24(9): 2599-2609. DOI: 10.1007/s12205-020-1900-6. [24] ZHANG Heng, ZHOU Guo-xiang, WU Jun-liang. Mechanism for soil reinforcement by electroosmosis in the presence of calcium chloride [J]. Chemical Engineering Communications, 2017, 204(4): 424-433. DOI: 10.1080/ 00986445.2016.1273833. [25] MALEKZADEH M, LOVISA J, NAGARATNAM S N. An overview of electrokinetic consolidation of soils [J]. Geotechnical and Geological Engineering, 2016, 34(3): 759-776. DOI: 10.1007/s10706-016-0002-1. [26] SHEN Yang, FENG Jian-ting, SHI Wen, QIU Chen-chen. Consolidation behaviors of soft clay using vacuum preloading method in combination with electro-osmosis based on different shapes of EKG electrode [C]// International Conference on Geotechnical and Earthquake Engineering 2018: Geotechnical and Seismic Research and Practices for Sustainability (IACGE 2018). Chongqing, China: IACGE, 2019, GSP 304: 345-356. DOI: 10.1061/9780784482049.034. [27] MARTIN L, ALIZADEH V, MEEGODA J. Electro-osmosis treatment techniques and their effect on dewatering of soils, sediments, and sludge: A review [J]. Soils and Foundations, 2019, 59(2): 407-418. DOI: 10.1016/j.sandf.2018.12.015. [28] WANG Bao-tian, VU M Q. Improvement of silty clay by vacuum preloading incorporated with electroosmotic method [J]. Journal of Rock Mechanics and Geotechnical Engineering, 2010, 2(4): 365-372. DOI: 10.3724/SP.J.1235.2010.00365. [29] ZHANG Wen-gang, WU Chong-zhi, ZHONG Hai-yi. Prediction of undrained shear strength using extreme gradient boosting and random forest based on Bayesian optimization [J]. Geoscience Frontiers, 2020, 12(1): 469-477. DOI: 10.1016/j.gsf.2020.03.007. [30] PENG Jie, YE Han-ming, ALSHAWABKEH A N. Soil improvement by electroosmotic grouting of saline solutions with vacuum drainage at the cathode [J]. Applied Clay Science, 2015, 114: 53-60. DOI: 10.1016/j.clay.2015.05.012. [31] WANG Liu-jiang, HUANG Peng-hua, LIU Si-hong, ALONSO E. Analytical solution for nonlinear consolidation of combined electroosmosis vacuum-surcharge preloading [J]. Computers & Geotechnics, 2020, 121: 1-14. DOI: 10.1016/ j.compgeo.2020.103484. [32] WANG Jun, MA Jian-jun, LIU Fei-yu. Experimental study on the improvement of marine clay slurry by electroosmosis-vacuum preloading [J]. Geotextiles and Geomembranes, 2016, 44(4): 615-622. DOI: 10.1016/j.geotexmem.2016.03.004. [33] PENG Jie, XIONG Xiong, MAHFOUZ A H, SONG En-run. Vacuum preloading combined electroosmotic strengthening of ultra-soft soil [J]. Journal of Central South University, 2013, 20(11): 3282-3295. DOI: 10.1007/s11771-013-1852-9. [34] WANG Jun, ZHAO Ran, CAI Yuan-qiang. Vacuum preloading and electro-osmosis consolidation of dredged slurry pre-treated with flocculants [J]. Engineering Geology, 2018, 246: 123-130. DOI: 10.1016/j.enggeo.2018.09.024. [35] FU Hong-tao, CAI Yuan-qiang, WANG Jun. Experimental study on the combined application of vacuum preloading-variable-spacing electro-osmosis to soft ground improvement [J]. Geosynthetics International, 2017, 24(1): 72-81. DOI: 10.1680/jgein.16.00016. [36] QIU Chen-chen, SHEN Yang, LI Yan-de. Laboratory tests on soft clay using electro-osmosis in combination with vacuum preloading [J]. Chinese Journal of Geotechnical Engineering, 2017, 39: 251-255. DOI: 10.11779/CJGE2017S1050. (in Chinese) [37] SUN Zhao-hua, GAO Ming-jun, YU Xiang-juan. Vacuum preloading combined with electro-osmotic dewatering of dredger fill using electric vertical drains [J]. Drying Technology, 2015, 33(7): 847-853. DOI: 10.1080/ 07373937.2014.992529. [38] ESRIG M I. Pore pressure, consolidation and electro-kinetics [J]. Journal of the Soil Mechanics and Foundations Division, ASCE, 1968, 94: 899-922. DOI: 10.1061/JSFEAQ.0001178. [39] XU Wei, LIU Si-hong, WANG Liu-jiang, WANG Jun-bo. Analytical theory of soft ground consolidation under vacuum preloading combined with electro-osmosis [J]. Journal of Hohai University (Natural Sciences), 2011, 39(2): 169-175. DOI: 10.3876/j.issn.1000-1980.2011.02.010. (in Chinese) [40] WU Hui, HU Li-ming. Analytical models of the coupling of vacuum preloading and electro-osmosis consolidation for ground stabilization [J]. Journal of Tsinghua University (Science and Technology), 2012, 52(2): 182-185. (in Chinese) [41] WANG Liu-jiang, WANG Yao-ming, LIU Si-hong, YUAN Jing. 2D analytical solution of consolidation for vacuum preloading combined with electro-osmosis drainage considering reduction of effective voltage [J]. Chinese Journal of Rock Mechanics and Engineering, 2019, 38(S1): 3134-3141. DOI: 10.13722/j.cnki.jrme.2018.0025. (in Chinese) [42] SHEN Yang, FENG Jian-ting, QIU Chen-chen. Two-dimensional consolidation theory of vacuum preloading combined with electroosmosis considering the distribution of soil voltage [J]. Soil Mechanics Foundation Engineering, 2020, 57(1): 25-34. DOI: 10.1007/s11204-020-09633-8. [43] SHEN Yang, QIU Chen-chen, LI Yan-de. An analytical solution for two-dimensional vacuum preloading combined with electro-osmosis consolidation using EKG electrodes [J]. Plos One, 2017, 12(8): 1-15. DOI: 10.1371/journal.pone. 0180974. [44] SHEN Yang, FENG Jian-ting, SHI Wen. Effects of voltage gradients on electro-osmotic characteristics of Taizhou soft clay [J]. International Journal of Electrochemical Science, 2019, 14(3): 2136-2159. DOI: 10.20964/2019.03.06. [45] POTHIRAKSANON C, SAOWAPAKPIBOON J, BERGADO D T, THAN N Y. Reduction of smear effects around PVD using thermo-PVD [J]. Proceedings of the Institution of Civil Engineers Ground Improvement, 2008, 161(4): 179-187. DOI: 10.1680/grim.2008.161.4.179. [46] ABUEL-NAGA H M, BERGADO D T, CHAIPRAKAIKEOW S. Innovative thermal technique for enhancing the performance of prefabricated vertical drain during the preloading process [J]. Geotextiles & Geomembranes, 2006, 24(6): 359-370. DOI: 10.1016/ j.geotexmem.2006.04.003. [47] SUN Zhao-hua, WU Chang-jiang, BAO Hua. Coupling consolidation theory of vacuum preloading incorporated with electro-osmosis for electric vertical drains [J]. Science Technology and Engineering, 2018, 18(33): 197-202. DOI: 10.3969/j.issn.1671-1815.2018.33.031. (in Chinese) [48] CAO Yong-hua, GAO Zhi-yi, LIU Ai-min. Characteristics and development of electro-osmotic treatment for ground improvement [J]. Port & Waterway Engineering, 2008, 4: 92-96. DOI: 10.16233/j.cnki.issn1002-4972.2008.04.024. (in Chinese) (Edited by ZHENG Yu-tong) 中文导读 考虑土体电势分布影响的真空预压联合电渗耦合解析解 摘要:真空预压联合电渗加固技术能够充分发挥真空预压法和电渗法的优势,进而有效改善软基处理效果。研究表明,当采用真空预压联合电渗法加固软基时,土体电势呈现非线性分布规律。然而,目前有关该联合加固技术的理论研究尚未考虑土体电势非线性分布对软基处理过程的影响且在理论推导中通常假设土体电势为线性分布,显然,这与试验结果有所出入。对此,本文首先以阳极为研究对象建立了二维平面应变条件下真空预压联合电渗法耦合固结模型。在模型中考虑了井阻效应、真空荷载沿土层深度衰减以及土体电势非线性变化的影响。然后,基于实际土体电势分布规律分别给出了阳极影响区域内平均超静孔隙水压力和土体固结度的理论解析解。最后,结合具体的模型试验案例对该解析解的合理性进行了验证,证明了该解析解的准确性和科学性。该解析解能够合理预测真空预压联合电渗法处理过程中超静孔隙水压力和土体固结度的变化情况,能够为真空预压联合电渗加固技术后续的工程运用提供借鉴和参考。 关键词:真空-电渗;非线性分布;二维平面应变;耦合固结模型;孔隙水压力 Foundation item: Project(51979087) supported by the National Natural Science Foundation of China; Project(BK20180776) supported by the Jiangsu Natural Science Foundation, China; Project(202006710002) supported by the China Scholarship Council Received date: 2020-10-28; Accepted date: 2021-03-17 Corresponding author: SHEN Yang, PhD, Professor; Tel: +86-13611508045; E-mail: shenyang1998@163.com: ORCID: https://orcid.org/ 0000-0003-2776-4169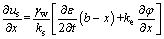 (13)
(13)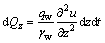 (14)
(14)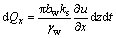 (15)
(15)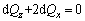 (16)
(16)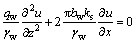 (17)
(17)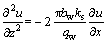 (18)
(18)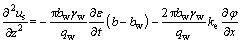 (19)
(19)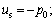
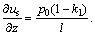
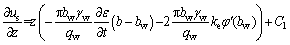 (20)
(20)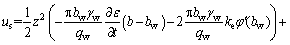
 (21)
(21)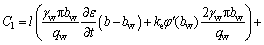
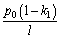 ,
, 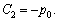
 (22)
(22)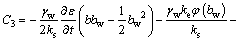
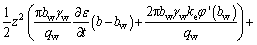
 .
.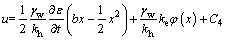 (23)
(23)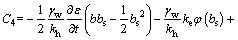
 .
.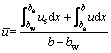 (24)
(24) (25)
(25)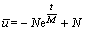 (26)
(26)



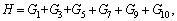 I=
I=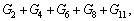
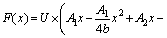
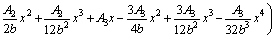 ,
, ,
,
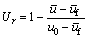 (27)
(27)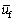 is the final value.
is the final value.