J. Cent. South Univ. Technol. (2008) 15(s1): 025-028

DOI: 10.1007/s11771-008-307-1

Identification of structure and parameters of rheological constitutive model for rocks using differential evolution algorithm

SU Guo-shao(苏国韶) ^{1, 2}, ZHANG Xiao-fei(张小飞) ¹, CHEN Guang-qiang(陈光强) ¹, FU Xing-yi(符兴义) ¹

(1.College of Civil and Architecture Engineering, Guangxi University, Nanning 530004, China;

2. State Key Laboratory of Geomechanics and Geotechnical Engineering , Institute of Rock and Soil Mechamics, Chinese Academy of Sciences, Wuhan 430071, China)

Abstract: To determine structure and parameters of a rheological constitutive model for rocks, a new method based on differential evolution (DE) algorithm combined with FLAC^3D (a numerical code for geotechnical engineering) was proposed for identification of the global optimum coupled of model structure and its parameters. At first, stochastic coupled mode was initialized, the difference in displacement between the numerical value and in-situ measurements was regarded as fitness value to evaluate quality of the coupled mode. Then the coupled-mode was updated continually using DE rule until the optimal parameters were found. Thus, coupled-mode was identified adaptively during back analysis process. The results of applications to Jinping tunnels in China show that the method is feasible and efficient for identifying the coupled-mode of constitutive structure and its parameters. The method overcomes the limitation of the traditional method and improves significantly precision and speed of displacement back analysis process.

Key words: rheological constitutive model; rocks; differential evolution algorithm; identification; FLAC^3D

1 Introduction

The rheological behavior is one of the important mechanical aspects of rock behavior. If this behavior is ignored in rock engineering design, disasters may occur^[1]. The Vajont landslide in Italy^[2] is a good example. Thus, research on determination of an appropriate rheological model and its parameters is one of the most important topics in rock mechanics. The traditional method is that the structure of the model is determined firstly according to certain mechanisms or experiences and then the parameters are recognized^[3-5]. Naturally, if the structure of the model itself is not correctly specified, even though the parameters are accurate, the model will not be able to comprehensively describe the mechanical responses of the actual rock materials^[6-7]. Therefore, it is necessary to fulfill simultaneous recognition of the structure of the model and its parameters in order to overcome the limitation of the traditional method. However, recognition of the structure of the model and its parameters is a optimization process with multi-variables and a large-scale search space. It is always impossible to find global optimum solution by using the classical algorithms such as gradient methods that merely provide a local optimum solution. Unlike classical methods, differential evolution (DE) algorithm^[8], as a newly developed optimization algorithm, has become a keynote optimization algorithm and been applied to optimization problems in different areas^[9-10].

In this paper, a method based on DE algorithm combined with FLAC^3D was proposed for coupled identification of the global optimum structure of the model and its parameters according to the idea of back analysis^[11].

2 DE algorithm

The main steps of the DE algorithm are given as follows.

1) Initialization. An optimization task consisting of D parameters can be represented by a D-dimensional vector. A population of NP solution vectors X_G = [x_{1, G}, x_{2, G}, …, x_NP,G] is randomly created at the start in feasible solution space.

2) Mutation. A mutant vector is produced by

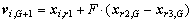              (1)

where  i, r₁, r₂, r₃∈{1, 2, …, NP} are randomly chosen and must be different from each other. The mutation factor F is a constant from [0, 2]. 

3) Crossover. The parent vector is mixed with the mutated vector to produce a trial vector:

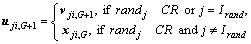       (2)

where  j=1, 2,…, D; rand_j~U[0,1] is the random number; CR is crossover constant; CR∈[0, 1] and I_rand is a random integer from [1, 2,…, D].

4) Selection. The target vector x_i,G is compared with the trial vector u_i,G+1 and the better one is selected to the next generation.

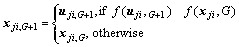        (3)

Mutation, recombination and selection continue until some stopping criterion is satisfied.

3 DE-FLAC^3D method

The method is described as follows.

Step 1: Set up numerical model for the given problem using FLAC^3D.

Step 2: Initialisation. Take natural number as code of different constitutive models. Consider code of given constitutive model and its mechanics parameters of the constitutive as coupled mode to be recognized. An optimization task consisting of D parameters can be represented by a D-dimensional vector X. A population of NP solution vectors is randomly generated initially at the given range according to empirical knowledge. The initial population is distributed uniformly in problem solving space.

Step 3: Mutation. For each target vector x_i,G , a mutant vector is produced by Eqn.(1).

Step 4: Recombination. Each trial vector is produced by Eqn.(2).

Step 5: Evaluation. Update constitutive model and its mechanics parameters for FLAC^3D numerical model. Perform FLAC^3D numerical calculations to obtain the fitness of each target vector and trial vector by

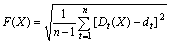               (4)

where  D_t(X) is the computed displacement at time t, as well as d_t is the measured displacement at time t; n is total number of sampling points which comes from displacement curve with intervals of 1 d.

Step 6: If the fitness of any vector is less than the maximum permissible error or the maximum evolution generation reaches the given upper bound, the identification process ends. The vector with minimum value of fitness is taken as the optimum solutions. Otherwise, using Eqn.(3) to obtain a new generation, go to Step 3.

The method was implemented by FISH programming language^[12], and was embedded within FLAC^3D.

4 Case study

Jinping II hydropower station is located in the mainstream of Yalong River, China. Four diversion tunnels with 17 km in length and 13 m in diameter run parallel with 60 m spacing among diversion tunnels (Fig.1). The buried depth of overlying strata is generally 1 500-2 000 m, the maximum buried depth reaches    2 525 m. Auxiliary tunnels, which are composed of two parallel single-lane tunnels with 35 m spacing, namely A and B tunnel, are located the south of diversion tunnels. The layout of measuring line at convergence measure- ments profile in B auxiliary tunnel is shown in Fig.2. DE-FLAC^3D method was used to fulfill identification  of coupled mode of structure and parameters of the constitutive model according to the measuring convergence displacement at profile that had been excavated. Then, the convergence displacement at profile that had not been excavated would be predicted according to the identification results. Thus, advance prediction

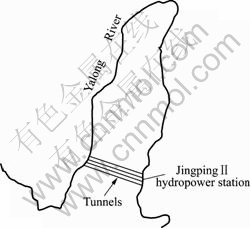
Fig.1 Layout of diversion tunnels

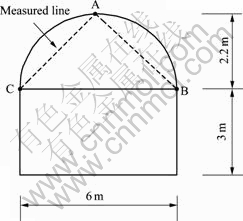
Fig.2 Measured profile of B auxiliary tunnel

of rock stability can be provided for safe construction and reasonable support design of the tunnel.

BK14+672 and BK14+565 profiles are taken as examples for case study. The three-dimensional geo-stress measurement and regression indicate that geo-stress at BK14+672 profile: the maximal principle stress is -41.9 MPa with 59? dip angle and almost vertical to axis of tunnel, the middle principle stress is -29.8 MPa with -2? dip angle and almost parallel to axis of tunnel, the minimum principle stress is -11.7 MPa with 21? dip angle and almost vertical to axis of tunnel; geo-stress at BK14+565 profile: the maximal principle stress is -42.5 MPa with 61? dip angle and almost vertical to axis of tunnel, the middle principle stress is -30.1 MPa with -2? dip angle and almost parallel to axis of tunnel, the minimum principle stress is -12.1 MPa with 19? dip angle.

The FLAC^3D numerical model and its coordinate axis location are shown in Fig.3. Along the tunnel direction an unit length is considered as a plane-strain problem. The size of the FLAC^3D numerical model is 80 m×80 m×1 m. Bottom border is constrained with vertical displacement and upper border is free border. Both left and right border are restrained with horizontal displacement, the same boundary conditions are applied in both the front and back borders in y-axis.

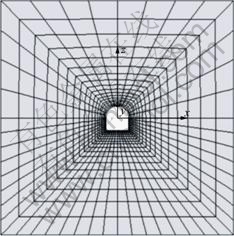
Fig.3 Grid of FLAC^3D model

The rock mass is marble with middle aplite and block structure. Marble is very hard and compact. Its Poisson’s ratio is 0.25, and density is 2 600 kg/m³.

Content of identification for rocks include structure of reheological constitutive model (including 8 classical reheological constitutive model which are represented by Index 1, 2,…,8), parameters of reheological constitutive model. Bounds of different model parameters are shown in Table 1. In Table 1, K is the spring’s stiffness, f is the friction coefficient, η is the viscosity coefficient, σ_s is the strength of a gliding slice. Constitutive models expect for Index 1-4 in Table 1 were written in C++^[12], and were added into FLAC^3D.

Table 1 Structure and parameters of model for identification

The difference in displacement curve of AC measuring line between the numerical results and measurements at BK14+672 profile was regarded as fitness value(Eqn.4).

The parameters for the DE algorithm were set to be: NP=10, F=2, CR=0.8，the minimum fitness f=0.2, the maximum evolutionary generation G=10.

When the evolutionary generation reaches 4, the optimum identification result is obtained: Burgers structure (shown in Fig.4) and corresponding parameters K₁=8.5 GPa, K₂=15.3 GPa, η₁=656 GPa·d, η₂=373 GPa·d. The simulation curve of the convergence displacement at AC measuring line is good in agreement with in-situ measurement (shown in Fig.5(a)), The error, namely fitness, F=0.178.

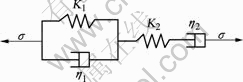
Fig.4 Structure of Burgers model

The Burgers model and its parameters were used to predict the convergence displacement at AC measuring line for BK14+565 profile (excavated after BK14+672) using FLAC^3D. The prediction is good in agreement with in-situ measurement (shown in Fig.5(b)), F=0.225.

  The results of case study indicate that the new method is feasible.

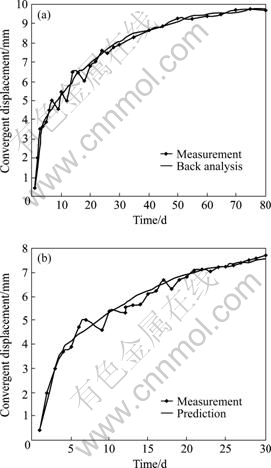
Fig.5 Comparison of convergent displacement curve of measurement along A-C measured line with (a) results of back analysis at BK14+672 profile and (b) predictions at BK14+565 profile

5 Conclusions

1) The results of applications to practical engineering show that the method based on DE algorithm is feasible and efficient for solving the problem about identification of the coupled-mode of constitutive structure and its parameters. The method overcomes the limitation of the traditional method and improves significantly precision and speed of displacement back analysis process with promising prospect in geotechnical engineering.

2) For easily application in practical engineering, 8 different structures of classical reheological constitutive models were considered in the paper. How to quickly search the globe optimum coupled-mode of constitutive structure and its parameters in more broad searching space made up of more different structure of reheological constitutive models is worth deeply researching.

References

[1] CHENG Zong-ji, KANG Wen-fa, HUANG Jie-fan. On the locked in stress, creep and dilatation of rocks and the constitutive equations [J]. Chin J Rock Mech Eng, 1991, 10(2): 299-312(in Chinese).

[2] ZHONG Li-xun. Enlightenments from the accident of violent landslide in Italy [J]. Chin J Geol Hazard Control, 1994, 5(4): 77-84. (in Chinese).

[3] FENG Xia-Ting, YANG Cheng-xiang. Genetic evolution of non-linear material constitutive models [J]. Comput Methods Appl Mech Eng, 2001, 190(45): 5957-5973.

[4] GAO Wei, Zheng Yin-ren. Identification of the geo-material constitutive model based on genetic algorithm [J]. Chin J Rock Mech Eng, 2002, 21(1): 8-11. (in Chinese)

[5] FURUKAWA T, SUGATA T, YOSHIMURA S, HOFFMAN M. An automated system for simulation and parameter identification of inelastic constitutive models [J]. Comput Methods Appl Mech Eng, 2002, 191(21/22): 2235-2260.

[6] FENG Xia-ting, CHEN Bing-rui, YANG Cheng-xiang, ZHOU Hui, DING Xiu-li. Identification of visco-elastic models for rocks using genetic programming coupled with the modified particle swarm optimization algorithm [J]. Int J Rock Mech and Min Sci, 2006, 43(5): 789-801

[7] ZHU Zhen-de, XU Wei-ya. Visco-elastic constitutive model recognition of rock mass and its engineering application [J]. Chin J Rock Mech Eng, 2002, 21(11): 1605-1609. (in Chinese)

[8] STORN R, PRICE K. Differential evolution, a simple and efficient heuristic strategy for global optimization over continuous Spaces [J]. Journal of Global Optimization, 1997, 11(4): 341-359.

[9] BERGEY P K, RAGSDALE C. Modified differential evolution: a greedy random strategy for genetic recombination [J]. Omega, 2005, 33(3): 255-265.

[10] KAELO P, ALIM M. A numerical study of some modified differential evolution algorithms [J]. European Journal of Operational Research, 2006, 169(3): 1176-1184.

[11] SU Guo-shao, FENG Xia-ting. Parameter identification of constitutive model for hard rock under high situ stress condition using particle swarm optimization algorithm [J]. Chin J Rock Mech Eng, 2005, 24(17): 3029-3034.(in Chinese)

[12] Itasca Consulting Group Inc. FLAC^3D User’s Manual (Version 3.0) [R]. Itasca Consulting Group Inc, 2005.

(Edited by ZHAO Jun)

Foundation item: Project (50809017) supported by the National Natural Science Foundation of China

Received date: 2008-06-25; Accepted date: 2008-08-05

Corresponding author: SU Guo-shao, Associate Professor, PhD; Tel: +86-771-3231316; E-mail: suguoshao@163.com